考慮匹配均衡性的供需雙方多對多雙邊匹配決策方法

王 娜 ，李引珍 ，柴 獲

（1. 蘭州交通大學機電工程學院, 蘭州730070；2. 蘭州交通大學交通運輸學院, 蘭州730070）

隨著我國交通行業和互聯網信息技術的快速發展，物流服務信息化水平和專業能力得到了大幅度提高. 物流服務行業的迅速發展，有助于提升產品的運輸效率，降低企業物流成本，提升企業自身的核心競爭力. 在激烈的競爭中，物流服務需求方的目標是用最低的成本獲得最滿意的物流服務，而物流服務供給方要在物流需求方滿意的同時追求較高的利潤，供需雙方的交易是典型的不交叉關系，兩者的匹配決策為自主自愿的市場化運作，其合作特征符合雙邊匹配理論基本要求，適用雙邊匹配理論和匹配決策方法進行研究分析.

在物流服務供需雙邊匹配決策問題中，通常物流服務供需匹配的供方或需方需要對對方做出一定的偏好排序，即供給方或需求方需要具備對對方的“敏感性偏好”，在該問題的研究中，根據供需雙方各自的評價指標給出完全偏好序信息是常見的研究方法. 因此，基于完全偏好序的雙邊匹配問題研究備受關注，樊治平等[1]在基于完全偏好序信息的一對一雙邊匹配問題中,以雙邊主體的匹配滿意度最大構建了多目標優化模型，利用雙邊主體的最高可接受偏好序算法進行求解獲得匹配結果. 孔德財等[2]針對一對一雙邊匹配問題，考慮匹配的穩定性、公平性和滿意性，以匹配主體的滿意度最大及匹配主體間的滿意度絕對差異最小建立了多目標優化模型. 姜艷萍等[3]針對基于偏好序的雙邊匹配問題,提出了具有抗操作和抗自虧性的匹配方法.張笛等[4]在考慮匹配特征基礎上，提出了多重偏好下的一對一多階段雙邊匹配方法. Dalzell等[5]認為當用于匹配的分類變量有誤差時，可以同時估計回歸模型和匹配記錄，提出了一種貝葉斯匹配方法.Li等[6]提出了一種基于雙重猶豫模糊偏好信息的一對一雙邊匹配方法，在穩定匹配約束下，以雙方的滿意度最大、差異度最小建立多目標優化模型.Yu等[7]針對人事崗位匹配問題提出了新的直覺模糊Choquet積分聚2集算子，構建了一個直觀的模糊一對一雙邊匹配模型. 李銘洋等[8]針對基于序值偏好信息的一對多雙邊匹配問題構建了以匹配主體序值之和最小為目標的多目標優化模型.Zhang等[9]對多對多雙邊匹配的匹配因素進行了研究，構建了一種順序聯結反應模型. Chen等[10]研究了弱偏好序的多對多雙邊匹配問題，提出了一種新的Pareto穩定匹配算法. Klaus等[11]利用兩階段非揭示機制研究了多對多匹配問題. Zhang等[12]提出了一種基于失望理論的不完全模糊偏好序一對一雙邊匹配決策理論，構建了確定最佳匹配解的雙目標優化模型. Jiao等[13]考慮了多對多雙邊匹配中的激勵相容性問題. Fan等[14]考慮心理因素將預期的各代理對相對代理的偏好序數基于不確定偏好序數計算，根據失望理論得到可能的匹配結果.Chen等[15]提出了一種根據參與者的主觀偏好修正一些關鍵目標，有效地提高了雙邊參與者的滿意度.林楊等[16-19]也進行了相應的研究.

既有文獻對一對一、多對多雙邊匹配問題進行了一定的研究，主要從整體滿意度角度考慮匹配主體進行匹配，而對匹配主體中個體的滿意度及其均衡性較少涉及，個體滿意度未得到充分滿足，很難保證匹配的公平性. 在保證整體滿意度前提下，考慮雙邊匹配主體中個體在匹配中的滿意度，主體中個體的匹配滿意度較均衡時才能達到公平的雙邊匹配.鑒于此，本文充分考慮整體滿意度和個體滿意度，構建基于完全偏好序物流服務供需多對多雙邊匹配兩階段優化模型，并基于NSGA-Ⅱ（non-dominated sorting genetic algorithm-Ⅱ）和線性規劃方法設計模型求解算法.

1 問題描述

假設所有物流服務供需雙方都要接受決策者的指令，決策者給出多種匹配方案后，物流服務供需方根據各自不同的偏好選擇匹配方案. 假設在物流服務供需雙方數量充足的情況下，物流服務需求方其集合為A={A1,A2,···,Am}（+m≥2），Ai表示第i個物流服務需求方，i=1,2,···,m；物流服務供給方其集合 為B={B1,B2,···,Bn}（+n≥2) ，Bj表 示 第j個 物 流服 務 供 給 方，j=1,2,···,n. 則I={1,2,···,m} ，J={1,2,···,n} . 設Ri=(ri1,ri2,···,rin) 為需求方Ai給出的關于供應方B的偏好序向量，其中rij為需求方Ai把供應方Bj排在第rij位. 設Tj=(t1j,t2j,···,tmj)為供應方Bj給出的關于需求方A偏好序向量，其中tij為需求方Bj把供給方Ai排在第tij位.

1.1 參數和變量定義

基于完全偏好序的物流服務供需雙邊匹配模型中的相關參數與變量定義如下：

αij——第i個物流服務需求方Ai對第j個物流服務供應方Bj的滿意度；

βij——第j個物流服務供應方Bj對第i個物流服務需求方Ai的滿意度；

pi——與第i個物流服務需求方匹配的供應方最大個數；

qj——與第j個物流服務供應方匹配的需求方最大個數；

hi— —與第i個物流服務需求方匹配的供應方個數；

lj— —與第j個物流服務供應方匹配的需求方個數；

xij——第i個物流服務需求方Ai與第j個物流服務供應方Bj匹配，0-1變量，其中xij= 0表示Ai與Bj不匹配，xij= 1表示Ai與Bj匹配.

1.2 物流服務供需方滿意度

αij和 βij的表達式如下：

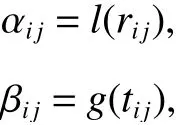
式中：l(?) 和g(?) 均為單調遞減函數.

按照完全偏好序的物流服務供需方雙邊匹配問題的描述，本文規定物流服務供需雙方偏好序的倒數即為物流服務供需雙方對對方的滿意度，則滿意度 αij和 βij可分別表示為

基于完全偏好序向量Ri和Tj，分別建立完全偏好序矩陣與. 依據式（1）和式（2），完全偏好序矩陣R與T分別轉化為完全滿意度值矩陣與

2 模型構建

本文構建多對多物流服務供需雙邊匹配兩階段優化模型，第1階段以物流服務需求方的整體滿意度最大及物流服務需求方個體滿意度的方差最小構建匹配模型（同理建立物流服務供給方匹配模型），利用遺傳算法進行模型求解得到物流服務供需方理想點的雙邊匹配Pareto解集；第2階段構建以供需雙方滿意度與理想點滿意度差最小的多目標優化模型，利用遺傳算法進行模型求解得到雙邊匹配Pareto解集.

2.1 第1階段優化模型

1） 針對物流服務需求方A，依據滿意度值矩陣以物流需求方整體滿意度及個體滿意度為優化目標，令為物流服務需求方的個體滿意度平均值.

構建第1階段物流服務需求方優化模型1：

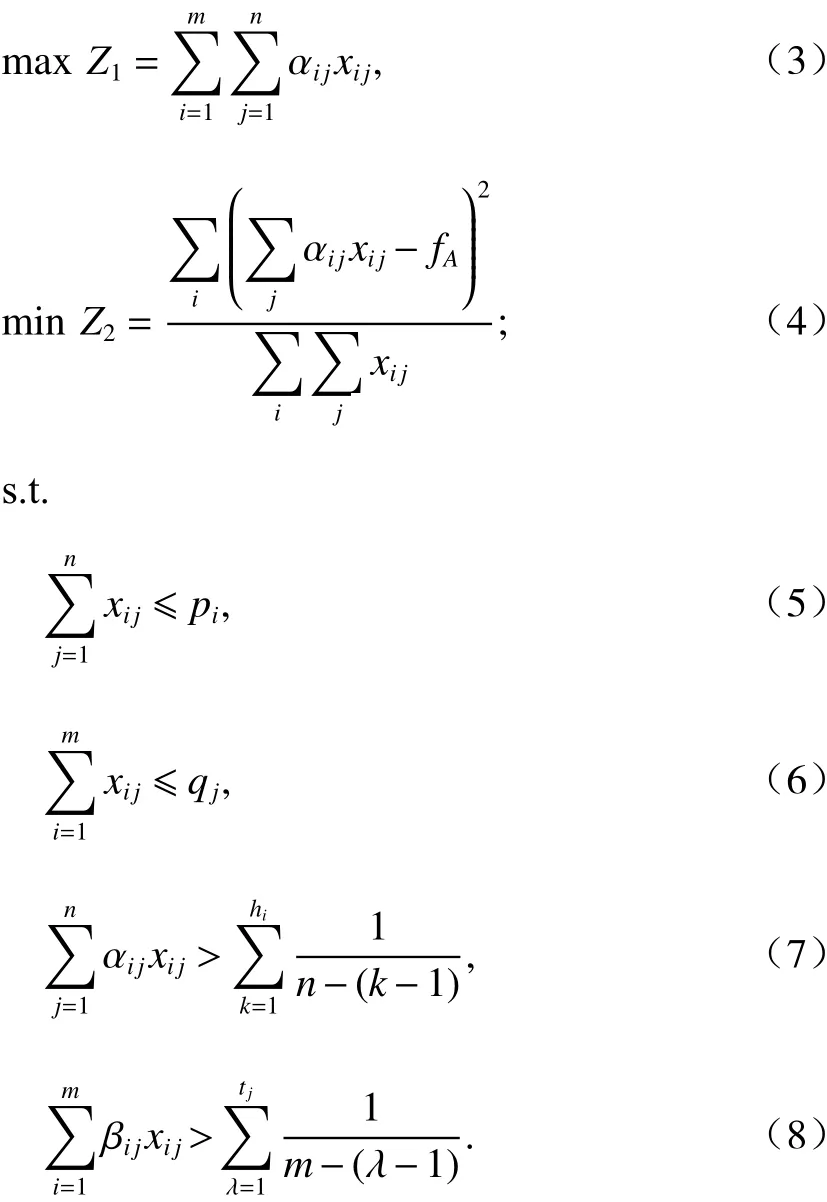
第1階段物流服務需求方優化模型1，只考慮物流服務需求方主體A總體滿意度和物流服務需求方Ai個體滿意度方差. 式（3）、（4）為目標函數；式（3）表示在嚴格雙邊匹配意義下最大化物流服務需求方主體A關于物流服務供給方主體匹配的總體滿意度，式（4）表示在嚴格雙邊匹配意義下物流服務需求方個體Ai與供給方個體Bj匹配，Ai的個體滿意度方差最小；式（5）表示每個物流服務需求方主體可以與多個物流服務供應方主體匹配；式（6）表示每個物流服務供給方主體可以與多個物流服務需求方主體匹配；式（7）保證物流服務需求方個體Ai匹配的供應方不是最差匹配（例如，與需求方A1匹配的供應方數量是2個，這2個供應方不能是需求方A1在滿意度排序中最后兩位的供應方），其中；式（8）保證物流服務供給方個體Bj匹配的需求方不是最差匹配，其中

2） 針對物流服務供給方B，依據滿意度值矩陣以物流供給方整體滿意度及個體滿意度為優化目標，令為物流服務供給方的滿意度平均值.

構建第1階段物流服務供給方優化模型2，模型2只考慮物流服務供給方主體B總體滿意度和物流服務需求方Bj個體滿意度方差，與模型1類似，這里不再贅述.

2.2 第2階段優化模型

第2階段模型中，考慮物流服務供需主體的整體滿意度與供需雙方在匹配時理想值的差值最小.構建第2階段優化模型3：

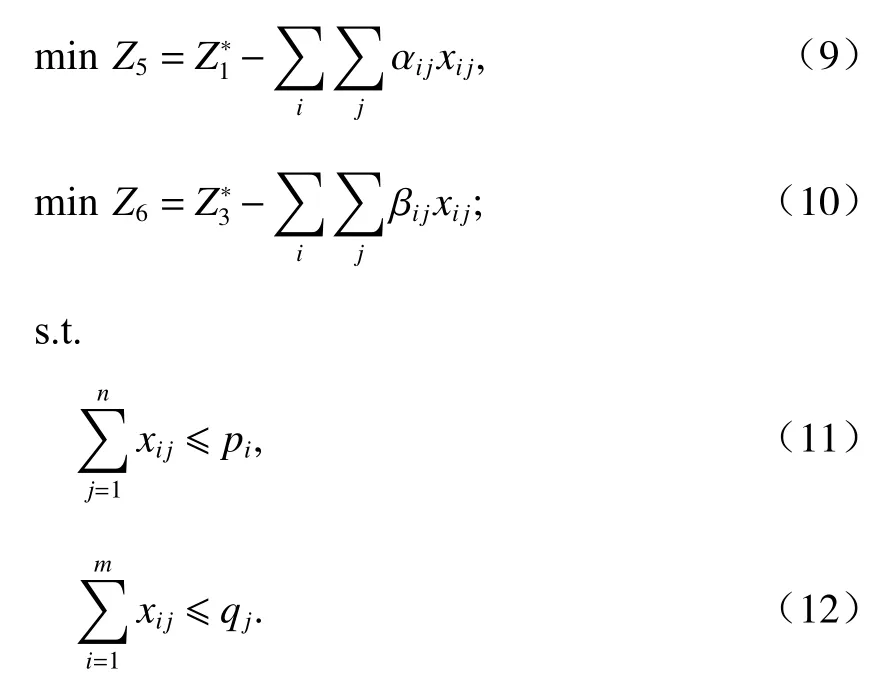
3 模型求解

3.1 第1階段模型求解

模型1為雙目標非線性0-1規劃問題，優化目標分別為整體滿意度Z1和個體滿意度Z2，由于Z2為非線性表達式，因此，該問題沒有精確算法. 解決此類問題的最好方法是基于NSGA-Ⅱ的多目標優化算法[20]. 本文將從以下3個方面進行算法設計.

1） 個體編碼

如圖1所示，個體采用多層0-1編碼，總長度為m×n，第i行第j列的編碼值如果為1表示需求方i和供應方j匹配，否則為兩者不匹配. 對于第i行編碼，其和必須小于等于pi，表示與物流服務需求方Ai匹配的供給方個數最多不超pi；同理，對于第j列編碼，其和必須小于等于qj.

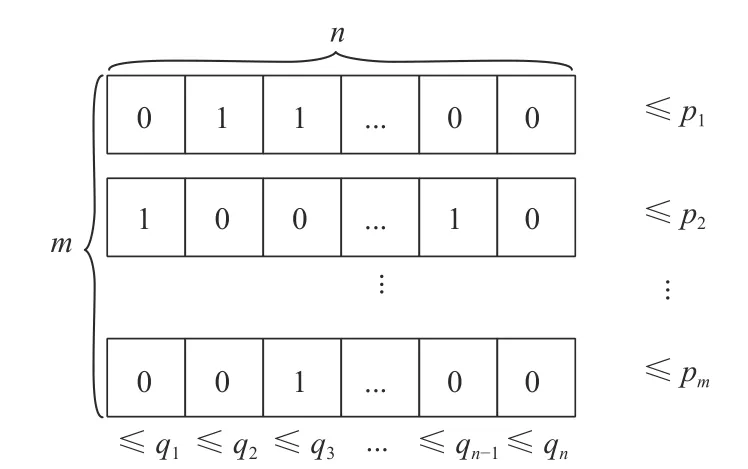
圖1 個體編碼Fig. 1 Individual encoding

2） 適應度函數

針對物流服務需求方，Z1為整體滿意度，優化目標為整體滿意度最大，可采用 1 /Z1作為該目標的適應度函數，Z2為個體滿意度，優化目標為個體滿意度差異最小，可采用Z2直接作為該目標的適應度函數.

3） 種群進化策略

一般情況下，通過交叉獲得新個體的方法來保證在進化過程中群體多樣性. 由于本模型中個體的行和列均有約束，個體的合法性采用慣常的交叉方法無法得到保證，基于上述考慮，設計一種能夠滿足模型中約束條件的行（列）交叉算子，計算步驟如下：

步驟1隨機選中兩個父個體，交換其奇數行（列）生成兩個子個體；

步驟2針對每一個子個體，從0到n（m）循環檢查其第j列（第i行）是否滿足條件

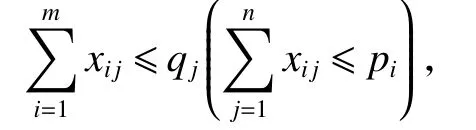
如果全部滿足，則所有子個體均為合法個體；

步驟3對于非法個體，選擇不滿足步驟2中條件的列（行），定位其奇數行中第1 次出現元素1的行列值，嘗試與本行（列）第1個元素0交換位置，交換后分別檢查交換列（行）是否滿足步驟2中條件，如果滿足，則修正后的子個體合法，如果不滿足，重新嘗試與本行（列）其他元素0交換位置，再次檢查，直到條件滿足.

以某物流供需服務為例，共有4個物流服務需求方和6個物流服務供給方，4個物流服務方可匹配的供給方個數分別不超過2、3、2、2，6個物流服務供給方可匹配的需求方個數分別不超過2、2、2、2、2、1. 以如圖2所示兩個父個體的行交叉為例，首先將父個體1和父個體2的第1、3行交換，生成子個體1和子個體2，下一步分別檢查子個體1和子個體2的合法性.

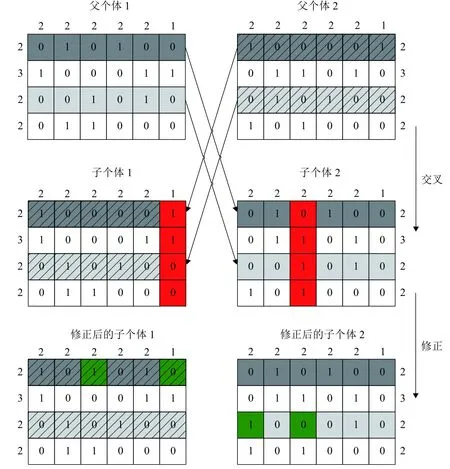
圖2 行交叉示例Fig. 2 Example of row-cross operator

對于子個體1，第6列的元素和為2，不滿足可匹配的需求方個數約束，需要進行修正，第6列第1個元素1出現在第1行，首先與第1行第2列的元素0交換，交換后分別檢查第2列和第6列，第6列元素和為1，滿足要求，但第2列元素和為3，不滿足可匹配的需求方個數約束，再次嘗試第1行第3列的元素0交換，交換后分別檢查第3列和第6列，均滿足可匹配的需求方個數約束，子個體1合法. 同理，對于子個體2，行交叉后也不滿足可匹配的需求方個數約束，將第3列第3行的元素1和第1列第3行的元素0交換后，個體合法.

為防止早熟收斂，在交叉的基礎上引入適度的變異. 變異操作采用行（列）交換變異法得到新個體，核心思想是隨機選擇個體，同時基于隨機方法選擇兩行（列），將被選個體的選中行進行交換，生成一個新個體，并檢查個體的合法性. 如果個體非法，從導致個體非法的行中找到第1個元素1，與被交換行中的相同位置元素交換位置，交換后分別檢查交換列（行）是否滿足步驟2中條件，如果滿足，則修正后的子個體合法，如果不滿足，繼續在導致個體非法的行中查找元素1，與被交換行中的相同位置元素交換位置，再次檢查，直到條件滿足.

以圖3所示個體為例，選中個體的2、3行，進行交換，交換后第2行滿足可匹配的需求方個數約束，但第3行元素之和為3，不滿足可匹配的需求方個數約束，在第3行中查找第1個元素1，其位于第3行第1列，與第2行第1列元素進行交換，交換后2、3行同時滿足可匹配的需求方個數約束，個體合法.

3.2 第2階段模型求解

針對第1階段優化得到的Pareto最優解中，根據對整體滿意度和個體滿意度的偏好，供需雙方決策者分別選擇合理的整體滿意度作為第2階段模型的理想點和，多目標函數的最優值與理想點的距離越接近越好，利用線性規劃方法求解.

加權將多目標優化模型轉化為單目標優化模型4：

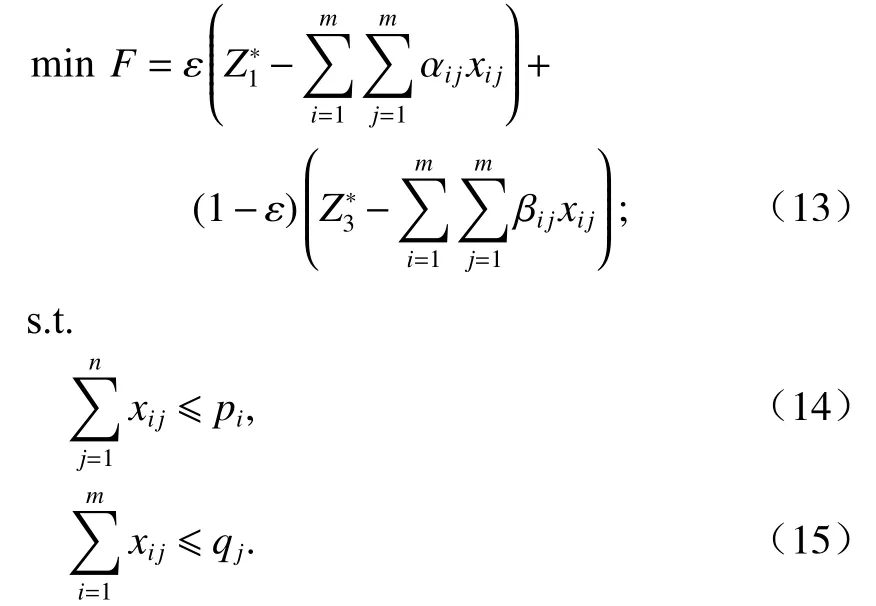
在現實的物流服務雙邊匹配問題中,ε 和1?ε可被分別視為物流供需雙方主體的重要程度，通常由中介依據物流供需雙邊主體的地位來考慮如何確定權重. 若認為物流供需雙邊主體在匹配過程中處于平等地位，則有 ε= 0.5. 若認為物流供需雙邊主體在匹配過程中的地位不同，即一方主體與另一方主體相比在匹配過程中顯得更重要，則有 0 ≤ε≤1，ε 取值從0.0001～1.0000，以步長0.0001循環，通過線性規劃方法進行求解，可獲得多對多物流服務供需雙邊匹配的Pareto解集.

4 算例分析

某 地 區 的 中 介 公 司 收 到(A1,A2,A3,A4,A5,A6)6個物流服務外包公司的相關需求信息，而中介公司里有(B1,B2,B3,B4,B5) 5個物流企業的信息. 相關供需雙方的滿意度排序見表1和2.

針對表1和表2的排序信息，假設每個物流服務需求方A可選擇服務供應方最大數量分別為2、3、2、4、2、1，而物流服務供應方B可向需求方提供匹配的最大數量為3、2、2、2、1. 根據求解方法，在第1階段考慮個體滿意度，分別針對需求方A和供給方B進行優化，可分別獲得供需雙方的整體滿意度和個體滿意度Pareto前沿（如圖4、5所示）.

表2 供給方B對需求方A的排序Tab. 2 Preference list of supplyB versus demandA

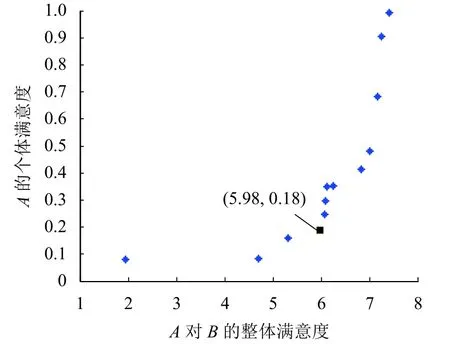
圖4 需求方A的整體滿意度與個體滿意度Pareto最優前沿Fig. 4 Pareto optimal front of overall satisfaction and individual satisfaction of demandA

假設需求方A和供給方B可接受的個體滿意度閾值均為0.22，則供需雙方可選擇的方案如圖4、5所示，供需雙方整體滿意度的理想點為5.98和5.23，在此理想點下，根據基于理想點的模型求解方法，可獲得如圖6所示的整體滿意度Pareto最優前沿.

對于圖6中整體滿意度Pareto最優解，可獲得需求方A對供給方B間的匹配關系，假設供需雙方可接受的整體滿意度值為(5.93,5.20)，則匹配關系如圖7所示.

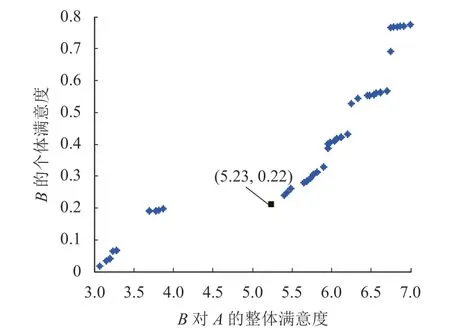
圖5 供應方B的整體滿意度與個體滿意度Pareto最優前沿Fig. 5 Pareto optimal front of overall satisfaction and individual satisfaction of supplyB

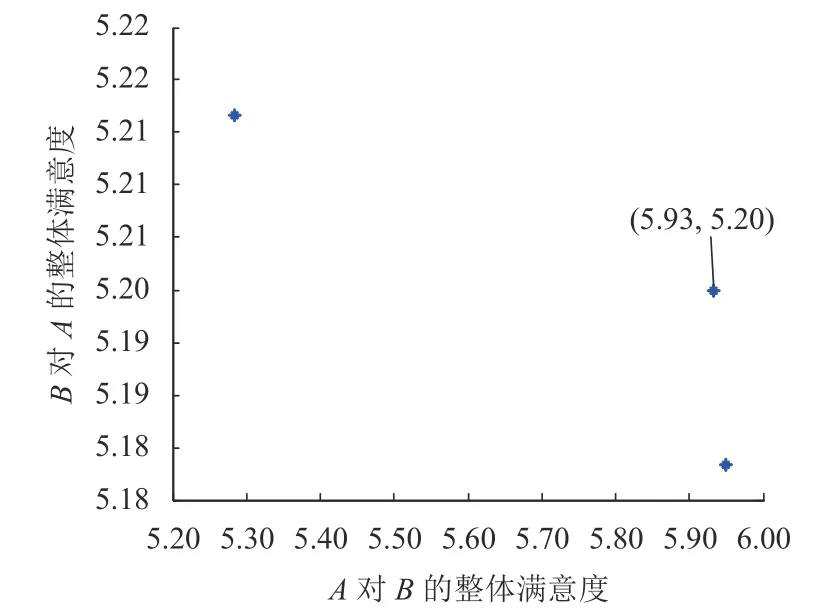
圖6 供需雙方個體滿意度限制下的整體滿意度Pareto前沿Fig. 6 Pareto optimal front of overall satisfaction constrained by individual satisfactions of supply and demand sides

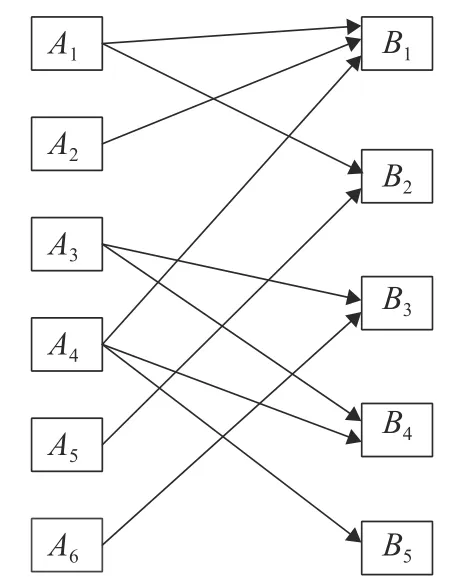
圖7 供需雙方整體滿意度為(5.93,5.20)下的匹配關系Fig. 7 Matching results of supply and demand sides with overall satisfaction (5.93,5.20)

當不考慮個體滿意度時，可以構建多對多物流服務供需雙邊匹配整體滿意度優化模型，以供需雙方匹配滿意度最大為目標函數的多目標優化模型，求解中先求出物流服務供需雙方不考慮對方滿意度的情況下自身的理想點滿意度，再通過物流服務供需雙方實際最大滿意度與理想點滿意度的差距最小建立多目標優化模型，利用線性規劃方法進行模型求解得到雙邊匹配Pareto解集. 基于NSGA-Ⅱ的多目標優化算法獲得整體滿意度和個體滿意度的Pareto解，為決策者提供了體現整體和個體滿意度不同偏好的決策方案，指導決策者獲得供需雙方滿意的匹配關系.

根據基于理想點法對算例求解，其理想點為(7.33,6.75)，可獲得如圖8所示的整體滿意度Pareto最優前沿.

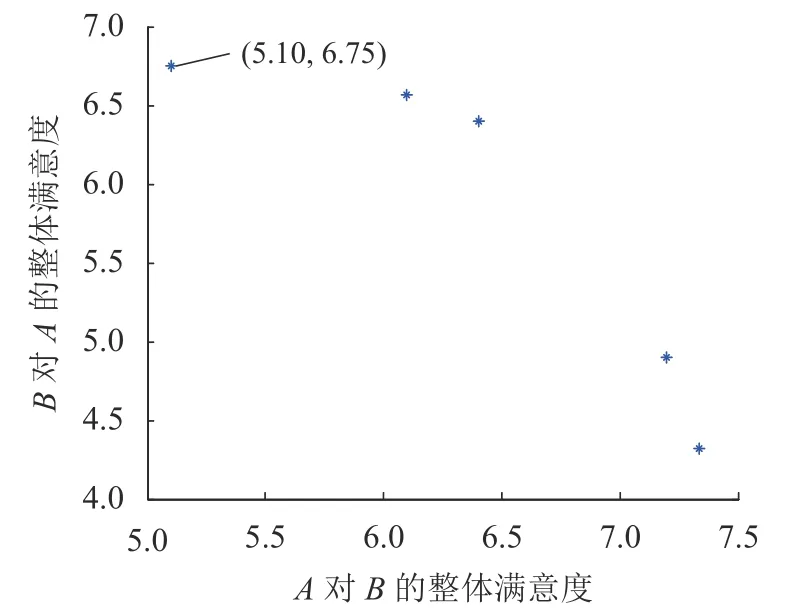
圖8 供需雙方整體滿意度Pareto前沿Fig. 8 Pareto optimal front of overall satisfaction of supply and demand sides

從圖8中可以看出：需求方A對供給方B的整體滿意度和B對需求方A的整體滿意度是此消彼長的關系，即需求方A對供給方B取最大整體滿意度時，供給方B對需求方A的整體滿意度最低，因此，在決策過程中，需要供需雙方談判以獲得彼此可接受的滿意度.

對于圖8中任意解，可獲得需求方A對供給方B間的匹配關系，如供需雙方可接受的滿意度值為(5.10,6.75)，則匹配關系如圖9所示. 在此匹配關系下，需求方A和供給方B的個體滿意度方差分別0.57和0.22，個體滿意度越小，表示個體之間的差異越小，對于本方案，需求方A的個體滿意度差異較大，選擇此方案導致需求方之間滿意度不公平，容易導致矛盾產生.

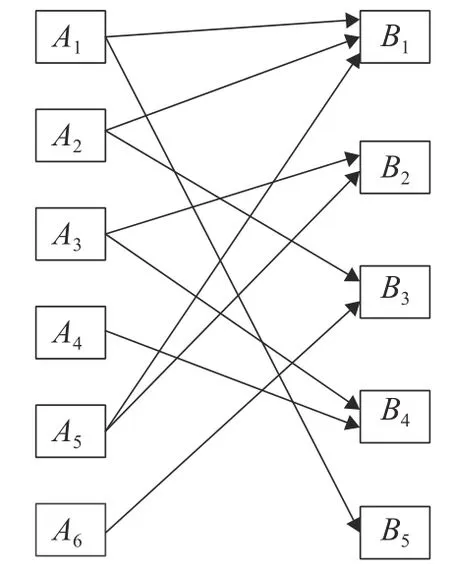
圖9 供需雙方整體滿意度為(5.10,6.75)下的匹配關系Fig. 9 Matching results of supply and demand sides with overall satisfaction (5.10, 6.75)

由圖6與圖8的Pareto前沿對比可以看出：考慮個體滿意度差異的情況下得到的整體滿意度明顯劣于未考慮個體滿意度的情況，相對未考慮個體滿意度情況，引入個體滿意度時會導致雙方整體滿意度下降，即為使每個個體能夠得到滿意、公平的匹配結果，需要犧牲雙方的整體的滿意度. 表明考慮個體滿意度最優時，整體滿意度會受到一定的影響，但其結果更貼近現實情況，并能得到公平的匹配結果，因為個體滿意度離理想點越近，匹配結果越接近個體對匹配結果的期望.

5 結 論

本文中同時考慮整體滿意度和個體滿意度均衡性的供需雙方多對多雙邊匹配兩階段優化模型，能夠刻畫物流服務中供需雙方的利益關系，既能考慮物流服務供需方整體滿意度，又兼顧供需方匹配個體滿意度的均衡性. 后續研究將考慮物流服務供需方個體差異化和優先級的穩定匹配問題，以提高實用性和適應性.