空氣物性對充氣式返回艙流場特性的影響

何青松, 王廣興, 王奇, 張 章, 王立武, 賈賀

(1.北京空間機電研究所, 北京 100094;2.中國航天科技集團有限公司 航天進入、減速與著陸技術實驗室, 北京 100094)

充氣式返回艙是一種新型的氣動減速裝置,再入大氣時利用充氣形成氣動外形,并由表面耐高溫柔性材料提供熱防護,最后由自身的充氣結構實現著陸緩沖。充氣式返回艙集合了傳統飛行器的熱防護系統、降落傘減速系統以及著陸/著水緩沖系統,簡化了航天器回收系統的設計[1]。充氣式返回艙拓展了傳統航天器回收著陸技術,具有廣泛的應用前景,各航天大國均開展了廣泛的研究[2-8],我國也在2020年5月用長征五號B運載火箭進行了首次柔性充氣式貨物返回艙搭載試驗。

不同于傳統的剛性結構返回艙,充氣式返回艙是由柔性材料制成,在高速氣流的沖擊下,柔性結構會發生變形甚至破壞。因此,充氣式返回艙的結構和防熱的設計十分重要,而獲得準確的流場特性參數是進行充氣式返回艙結構和防熱設計的重要前提。相比于實驗研究,數值模擬能夠快速獲得充氣式返回艙的流場特性參數,縮短研制周期,降低研制成本。為獲得準確可靠的充氣式返回艙流場特性參數,建立合理的數值仿真模型,選擇合理的物性參數十分重要。目前充氣式返回艙大氣再入氣動特性仿真大多基于理想氣體假設,黏性系數和熱導率等物性參數采用Sutherland公式[9-13]。通常情況,常溫下空氣的黏性和熱導率可采用Sutherland公式計算,但當溫度進一步升高時,空氣中的氧氣和氮氣將發生解離反應,更高溫度時將發生電離反應,這一系列的化學反應使空氣物性發生復雜變化,Sutherland公式將不再適用[14]。充氣式返回艙高速再入時流場溫度非常高[15],若采用Sutherland公式計算空氣物性參數會帶來巨大誤差。因此,為了獲得準確的氣動特性參數,首先需要獲得高溫下空氣的物性參數。

為解決高溫條件下空氣物性參數的計算問題,學者們已經進行了深入研究[16-19],目前應用較為廣泛的是Gupta的高溫空氣擬合關系式[17],該擬合關系式已經被廣泛應用于超聲速等離子體風洞、電弧加熱器、圓柱繞流以及平板邊界層流動等領域的研究[14,20-22]。

本文分別采用Gupta的高溫空氣擬合關系式和Sutherland公式計算空氣的物性參數,對充氣式返回艙高速再入流場進行數值模擬研究,比較采用這兩種空氣物性參數計算方法獲得的流場特性參數差異,進而為充氣式返回艙的工程設計提供一定的理論參考。

1 計算模型

本文采用二維數值模擬對充氣式返回艙氣動特性進行研究,求解可壓縮N-S方程,在笛卡爾坐標系下控制方程可以寫成如下形式

式中:ρ為流體密度；xi為笛卡爾坐標;ui為速度分量;p為壓強;E為內能;H為焓值;τij和qi分別為黏性應力項和熱通量項。

湍流模型采用k-ω模型,模型輸運方程如(4)～(5)式所示

式中,β′=0.09,α=1.4,β=0.075,σk=2,σω=2。

本文研究的流體介質為空氣,分別采用Sutherland公式和Gupta的擬合公式對方程中涉及到的物性參數進行計算。公式(6)和(7)為Sutherland公式表示的黏性系數和熱導率。Gupta擬合公式基于空氣11組分模型(O2,N2,O,N,NO,O+,N+,NO+,O2+,N2+,e)計算高溫空氣物性,考慮了空氣因高溫導致的空氣化學反應,溫度范圍最高達30 000 K[19]。公式(8)和(9)為Gupta擬合公式的黏性系數和熱導率。

(6)

(7)

(8)

(9)

式中:T,μ,κ分別為溫度、黏性系數和熱導率;μ0=1.716 1×10-5Pa·s,κ0=2.415×10-2W/(m·K);To=273.16 K,Tc=110.4 K,T0為攝氏零度,Tc為參考溫度,χμ,χκ,Aμ,Aκ等參數可參考文獻[19]。

本文以日本研制的充氣式返回艙實驗模型HWT-MAAC為研究對象,該模型為飛行演示驗證試驗中采用的充氣式返回艙SMAAC的縮比模型,其結構示意如圖1所示,尺寸參數可參見文獻[23]。

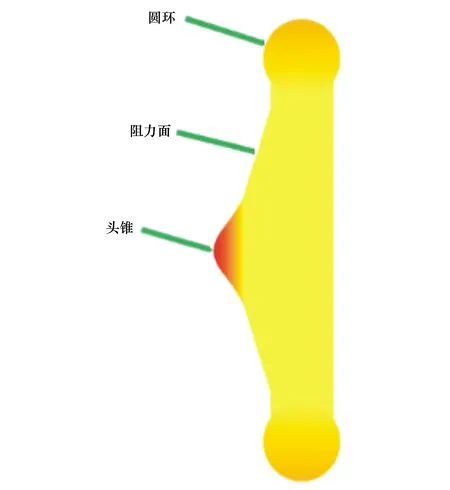
圖1 HWT-MAAC模型結構示意圖

為考察不同溫度范圍2種物性參數計算方法帶來的結果差異,本文在文獻[23]實驗工況的基礎上,通過改變來流溫度和馬赫數來進行計算研究。實驗工況為來流溫度45 K,來流馬赫數10,來流壓強均為60 Pa,表1列出了本文的5個計算工況,所有計算工況的來流攻角均為0°。

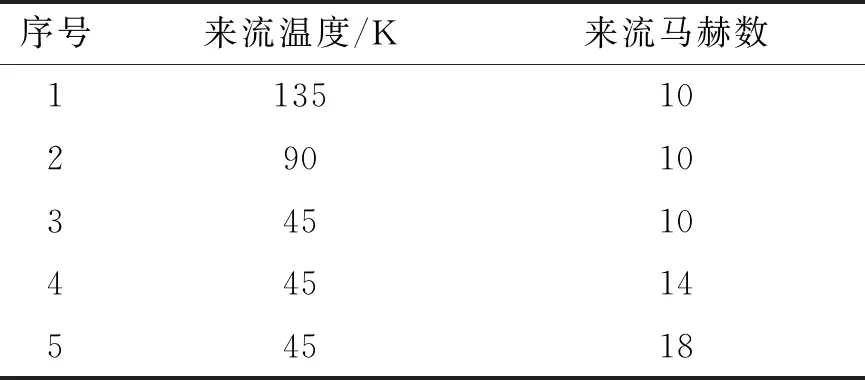
表1 計算工況

圖2給出了本文的計算域,計算域為半圓形,直徑約為返回艙直徑的10倍,返回艙前端距計算域前端約為2倍返回艙的直徑。本文的計算工況為超聲速流動,流場的擾動不會向上游傳播,計算域能夠捕捉完整的激波結構,則計算域的選取對計算結果的影響較小。計算域入口給定來流馬赫數、來流壓強以及來流溫度,出口參數外推,壁面采用無滑移邊界條件,壁面溫度為300 K。

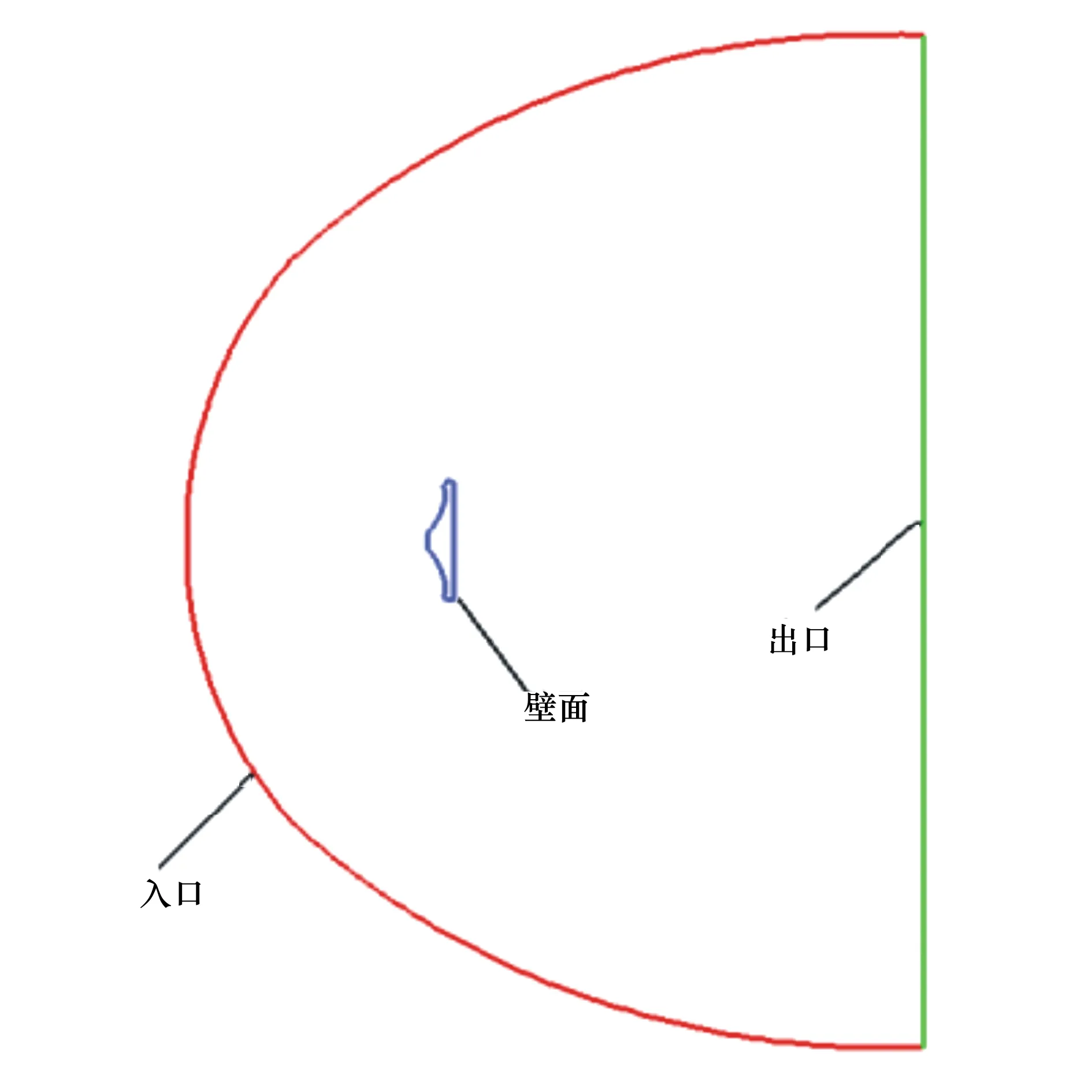
圖2 計算域以及網格劃分情況

2 計算結果

首先本文進行了網格無關性驗證,分別采用網格數為30 000,60 000以及120 000的網格數量對工況3進行了計算,同時對近壁網格進行加密保證y+小于1,比較了沿壁面的熱流密度,比較結果如圖3所示。從圖中可以看出網格數量為60 000和120 000的計算結果十分接近,而網格數量為30 000的計算結果與另外2個相差較遠。因此,為了能夠保證計算的準確性,同時也能節省計算資源,本文采用網格數量為60 000,圖4給出了網格劃分情況。

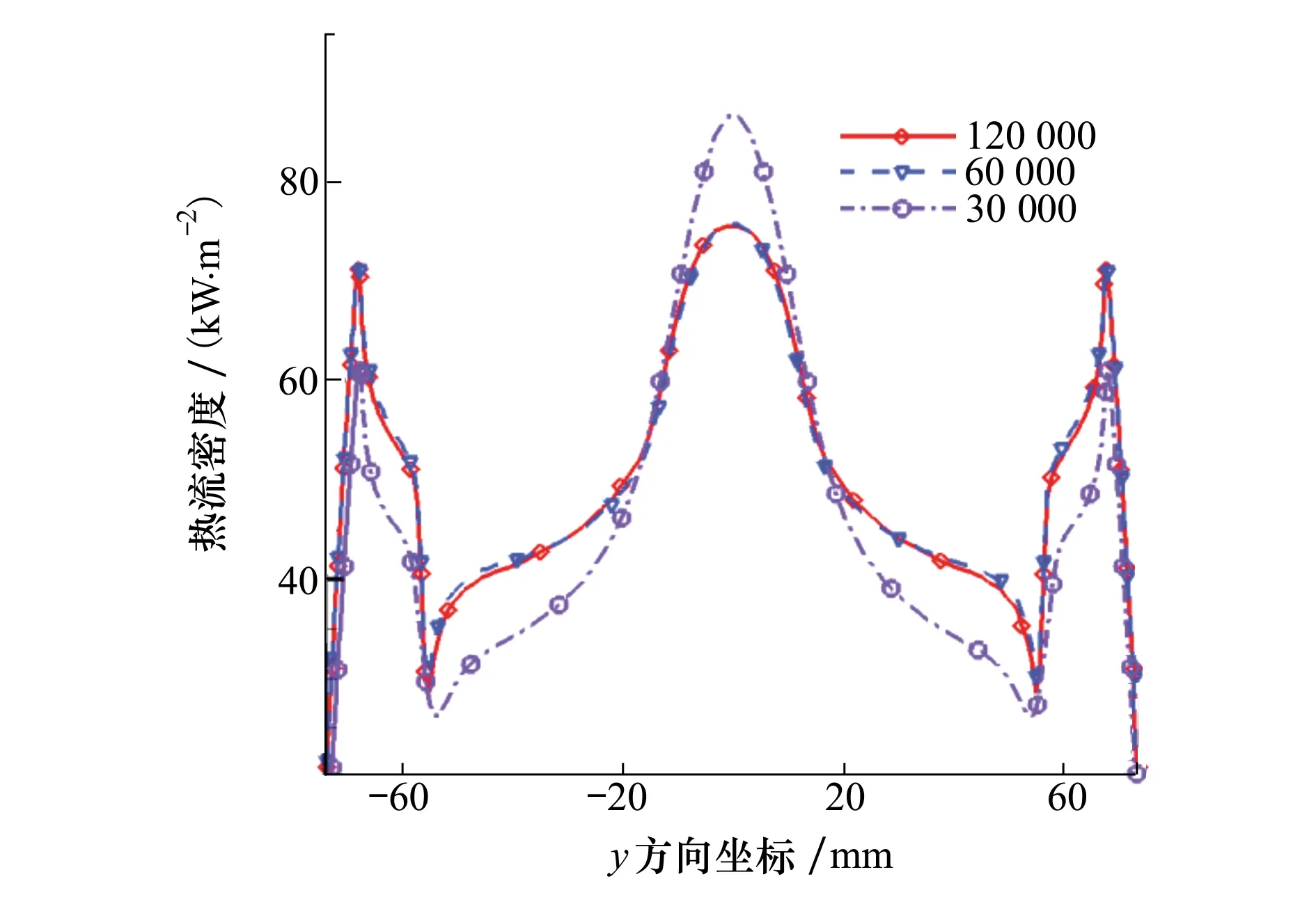
圖3 網格無關性驗證

圖4 網格劃分(網格量60 000)

為了驗證模型的可靠性,本文將工況3計算得到的充氣式返回艙迎風面的熱流密度與文獻[23]的實驗結果和三維仿真結果進行了比較,如圖5所示。實驗中采用高超聲速風洞對充氣式返回艙實驗模型HWT-MAAC進行了研究,采用輻射平衡假設對表面熱流密度進行測量。從圖中看出本文采用Gupta擬合公式和Sutherland公式的計算結果與實驗值均符合較好,在阻力面處,本文的計算結果比文獻[23]的仿真結果略高。

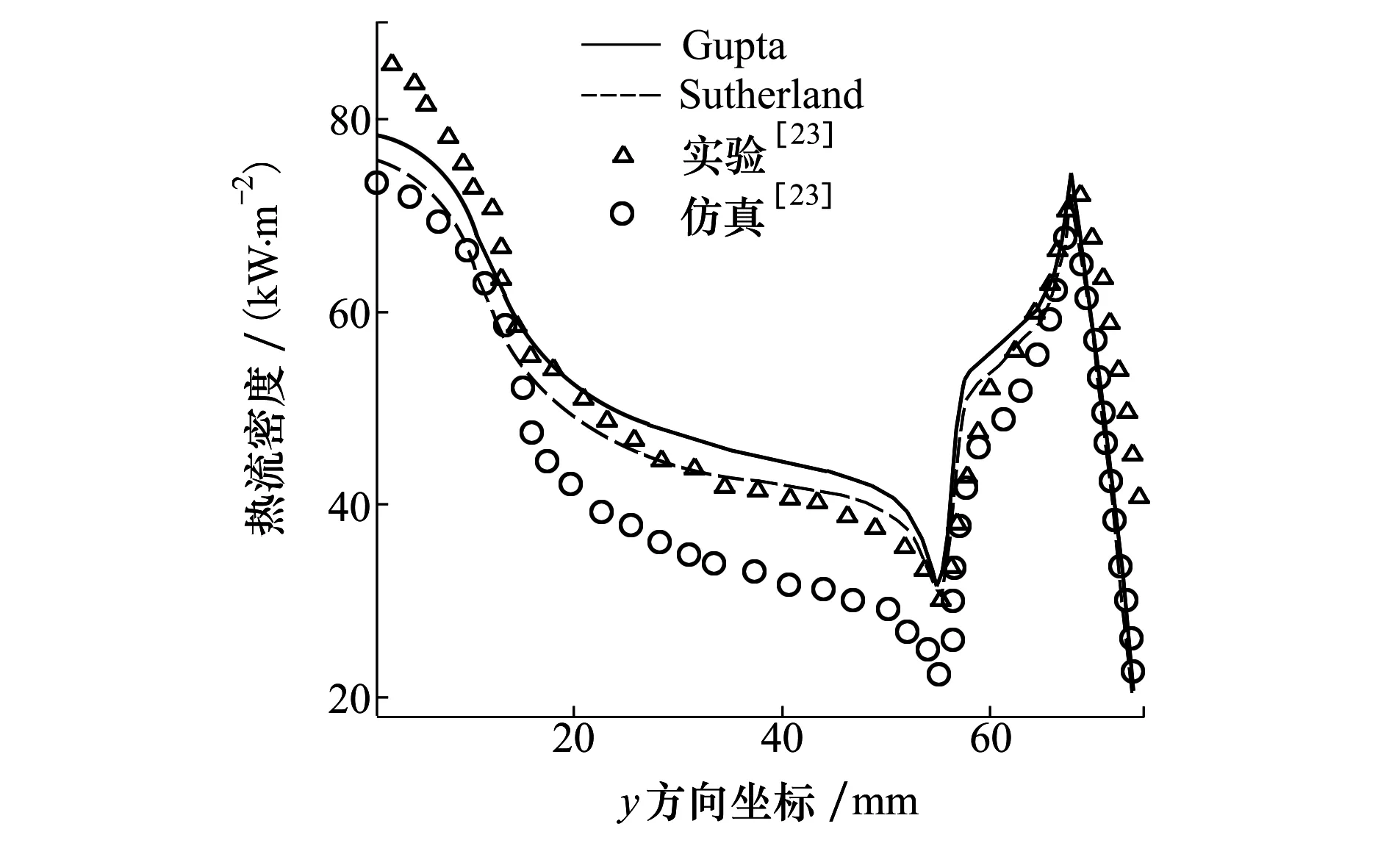
圖5 返回艙壁面熱流密度與文獻[23]結果比較

為進一步驗證本文模型的可靠性,本文選擇文獻[24]的實驗結果進行驗證,實驗模型為90 mm圓柱體,采用高焓激波風洞對圓柱體迎風面的熱流密度和壓強進行了測量,來流馬赫數為8.78,來流溫度694 K,來流壓強為687 Pa,比較結果如圖6所示。從圖中看出采用Gupta擬合公式獲得的表面熱流密度與實驗結果符合得更好,采用這兩種物性計算方法得到的表面壓強與實驗結果符合均較好。

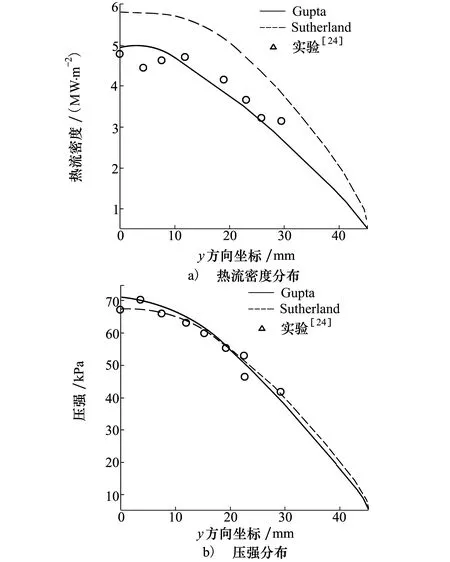
圖6 圓柱體計算結果與文獻[24]結果比較

溫度對空氣物性參數有十分重要的影響,圖7給出了本文計算工況的溫度分布情況,從圖中看出采用Gupta擬合公式計算得到的激波位置更靠近返回艙表面,流場的溫度也顯著比Sutherland的計算結果低。另外,從圖中還看出這種差異隨著來流馬赫數和溫度的增加更加明顯,比如工況3的來流馬赫數和溫度相對來說較低,Gupta擬合公式和Sutherland公式計算結果相對來說也較為接近。工況3中流場最高溫度不超過1 000 K,Sutherland公式還能較好地描述空氣的物性,Sutherland公式和Gupta擬合公式計算得到的空氣物性差別不大。而隨著來流馬赫數和溫度的增加,流場中的溫度逐漸上升,Gupta擬合公式和Sutherland公式計算得到的空氣物性參數差別較為明顯,兩者計算得到的流場特性差別逐漸顯現。

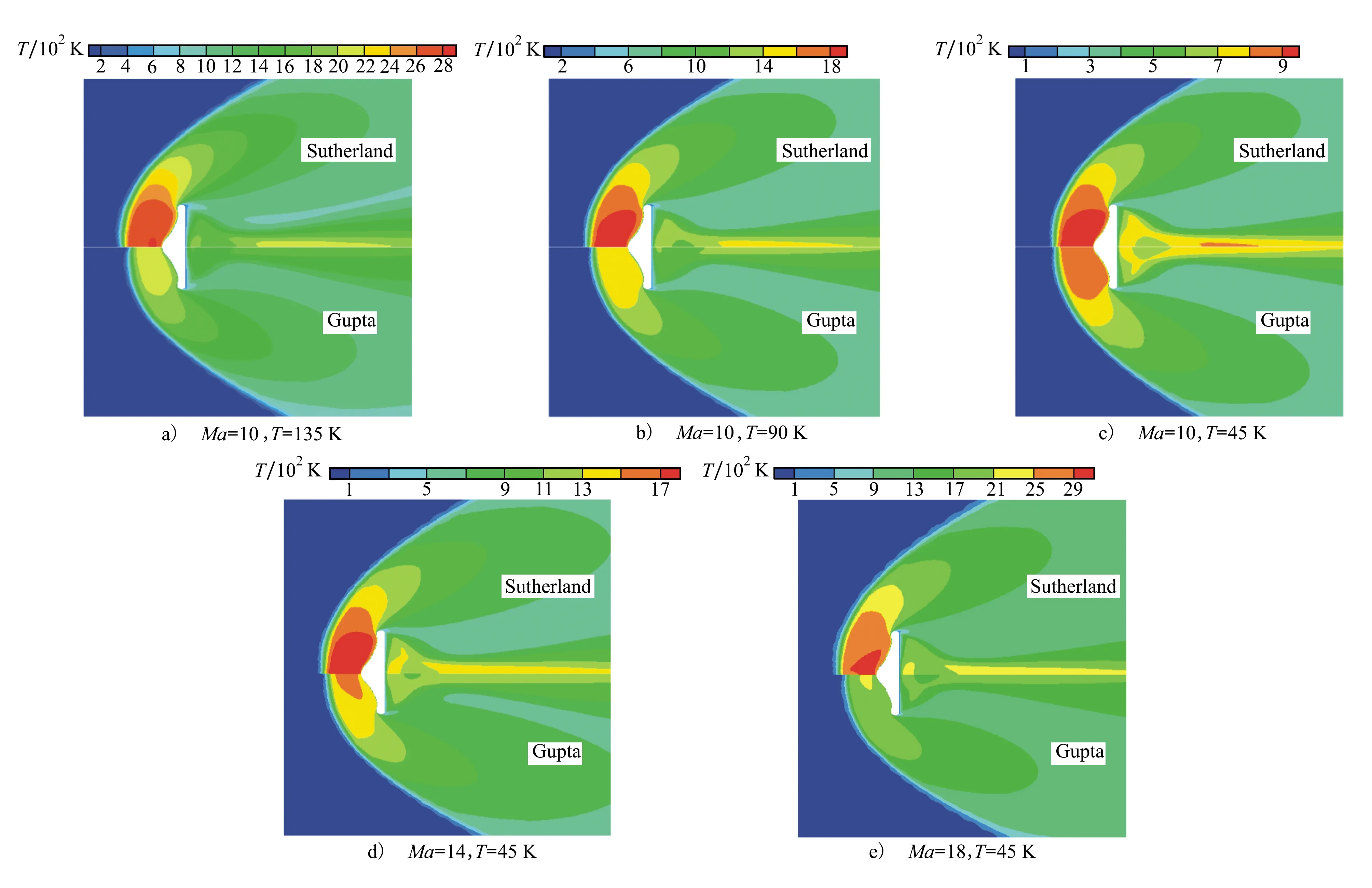
圖7 流場中溫度分布情況

對于高超聲速激波形狀和距離的研究始于20世紀50年代,涉及理論和實驗研究[25]。以大量實驗數據為基礎得出的激波脫體距離工程算法計算量小,計算速度快,Inouye[26]建立了多種氣體環境下的繞半球體脫體激波距離關系式如(10)式所示

(10)

式中：Δ為激波脫體距離；R為半球半徑；ρ∞和ρ分別為波前和波后氣體的密度。從這個關系式中可以發現,脫體激波的距離跟波前和波后氣體密度的比值成正比。為探究采用2種物性參數方法計算的激波位置產生差異的原因,圖8給出了沿流場中心線氣體的密度。從圖8中看出在波前采用2種物性參數計算方法得到的密度相差不大,而在波后Gupta擬合公式計算得到的氣體密度大于Sutherland公式計算得到的氣體密度,即Gupta擬合公式獲得的波前和波后的氣體密度的比值小于Sutherland公式,因此脫體激波的距離更接近物面。

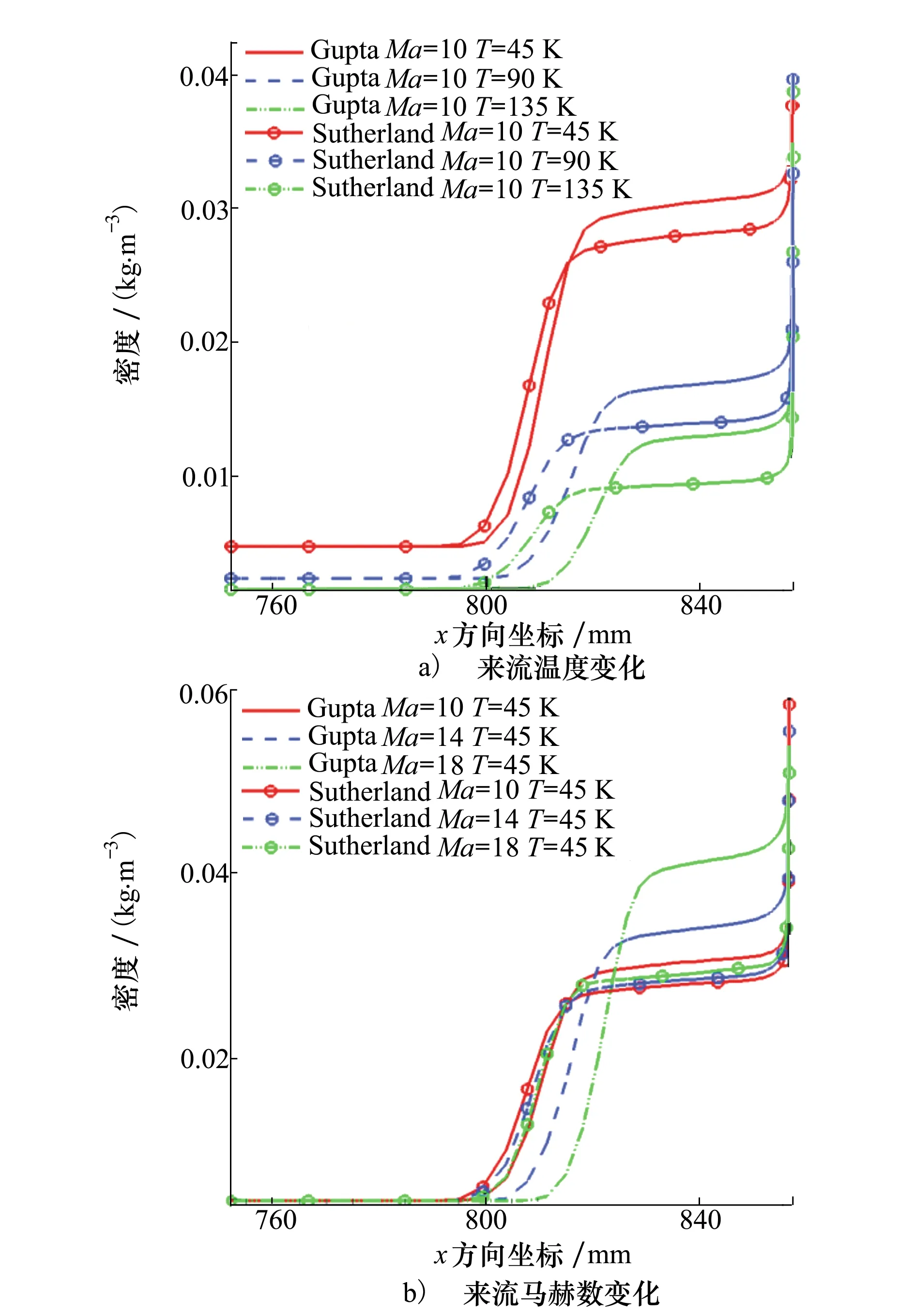
圖8 沿中心線氣體的密度

不管是來流馬赫數增加還是來流溫度的增加,流場溫度的上升是導致兩者計算結果差異的重要因素,表2列出了5個工況流場中的最高溫度,TG和TS分別表示采用Gupta擬合公式和Sutherland公式計算得到的最高溫度,比較發現隨著來流馬赫數和溫度的增加,流場中最高溫度的差距增加十分明顯。產生流場溫度差異的主要原因是Gupta擬合公式考慮了空氣高溫下因振動、解離以及電離等化學反應對物性參數的影響,空氣的這些化學反應能夠吸收返回艙外部的部分能量,導致返回艙外部溫度降低。

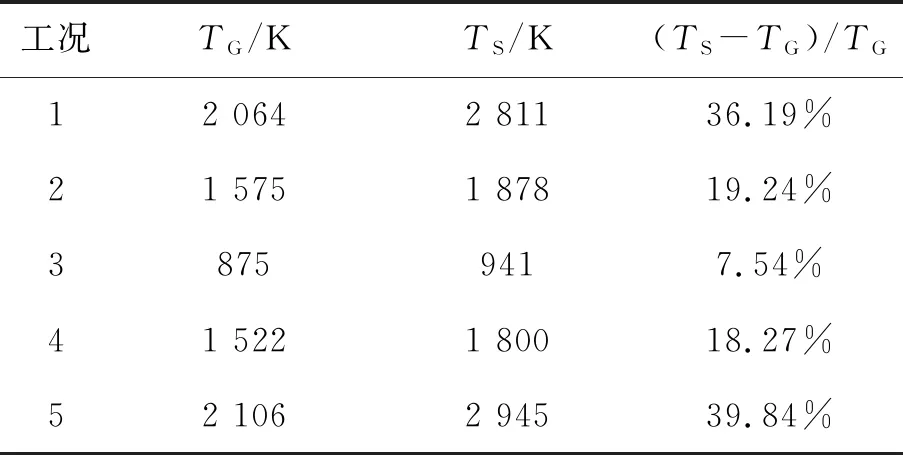
表2 流場中最高溫度比較

在高速氣流沖擊下,充氣式返回艙迎風面將承受劇烈的氣動力和氣動熱,準確的氣動熱和氣動力特性對充氣式返回艙的結構和防熱設計十分重要。圖9給出了返回艙迎風面的熱流密度分布,從圖中看出熱流密度在頭錐和兩側圓環處均存在峰值,最大峰值在頭錐處。從圖中還可以看出返回艙表面的熱流密度隨著來流馬赫數和溫度增加上升十分顯著,以Gupta擬合公式計算結果為例,來流Ma=10,T=45 K,頭錐處峰值的熱流密度為79 kW/m2,來流Ma=10,T=135 K, 頭錐處峰值的熱流密度為451 kW/m2,來流Ma=18,T=45 K,頭錐處峰值的熱流密度為1 022 kW/m2。比較發現,Sutherland公式計算的熱流密度總體上低于Gupta擬合公式的結果,Sutherland公式低估了返回艙表面的熱流密度,如工況5所示,來流Ma=18,T=45 K,Gupta擬合公式獲得的熱流密度峰值高出Sutherland公式獲得的熱流密度峰值29%。其中工況3由于兩者計算得到的流場溫度相差不大,兩者物性參數差別不大,Gupta公式的計算結果僅略微高于Sutherland公式的結果。

圖9 返回艙迎風面的熱流密度分布 圖10 返回艙迎風面的壓強分布

由于返回艙表面的氣動力主要來源于表面壓強的作用,圖10給出了返回艙迎風面處的壓強分布情況,從圖中看出壓強的分布規律與熱流密度的分布規律類似,在頭錐和兩側圓環處均存在峰值,最大峰值在頭錐處。從圖10a)中看出,來流溫度對迎風面的壓強影響并不大,迎風面壓強隨來流溫度增加僅略微增加。從圖10b)中看出,來流馬赫數對迎風面壓強影響較大,迎風面的壓強隨來流馬赫數的增加顯著上升。比較發現,Gupta擬合公式計算得到的迎風面壓強大于Sutherland公式的計算結果,但相對于表面熱流密度的差異,表面壓強的差距并不是很大。

充氣式返回艙的柔性熱防護系統通常由防熱層、隔熱層和阻力承力層構成,最外層的防熱層主要用來阻擋熱流密內部氣囊滲漏,保持充氣結構的形狀[27]。準確的氣動力和氣動熱特性是各層材料選擇以及材料鋪層數量選取的重要參考,Sutherland公式在高溫下不再適用,低估了充氣式返回艙表面的熱流密度和壓力,則有可能造成設計的充氣結構防熱性能和強度不足,因此在高溫環境下采用Gupta擬合公式進行研究更為合理。

熱導率是引起熱流密度差異的重要原因,以工況5為例,圖11給出了流場中的熱導率分布,從圖中看出Gupta擬合公式獲得的熱導率顯著高于Sutherland公式獲得熱導率,流場中最大熱導率分別為0.152和0.107 W/(m·K)。高溫下,空氣的熱導率由平動熱導率和反應熱導率組成,Gupta擬合公式考慮了空氣的反應熱導[19],因此采用Gupta擬合公式獲得的熱導率更大。由圖7可知,Sutherland公式計算得到的流場溫度更高,在近壁區域的溫度梯度也更高,但Sutherland獲得的近壁區域熱導率比Gupta擬合公式低,因此導致壁面的熱流密度更低。

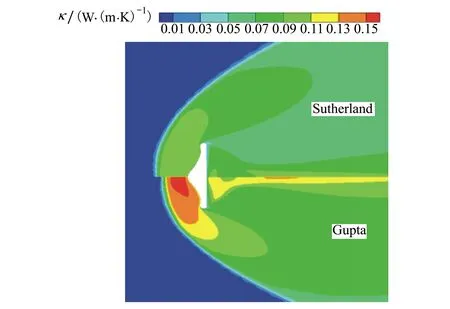
圖11 流場中熱導率分布情況

3 結 論

本文分別采用Gupta擬合公式和Sutherland公式計算空氣物性參數,比較了采用這兩種計算公式獲得的充氣式返回艙流場特性的差異,研究表明:①采用Gupta擬合公式獲得的激波位置比Sutherland公式的結果更靠近返回艙,這種差異在高來流馬赫數和溫度時更加明顯;②采用Gupta擬合公式獲得的流場溫度更低,且隨著來流馬赫數和溫度的增加,流場最高溫度的差異更加明顯;③Sutherland公式低估了返回艙迎風面的熱流密度,尤其在來流溫度和馬赫數較高的工況,Gupta擬合公式獲得的熱流密度顯著高于Sutherland公式的結果, 工況5中Gupta擬合公式獲得的熱流密度峰值高出Sutherland公式獲得的熱流密度峰值29%;④Sutherland公式獲得的迎風面壓強低于Gupta擬合公式的結果,但是壓強的差異相對于熱流密度的差異小很多。