某連續式超聲速風洞控制系統設計研究

陳旦, 王眾, 魯相, 林辰龍, 裴海濤

(中國空氣動力研究與發展中心 設備設計及測試技術研究所, 四川 綿陽 621000)

某連續式超聲速風洞作為國內首座連續式超聲速風洞，馬赫數范圍為1.5～4.5(目前馬赫數只到3.0)，壓力范圍20～200 kPa(絕壓)。風洞由多級壓縮機驅動，配置有噴管段、試驗段和超擴段等部段，同時配置總壓系統實現增壓和降壓運行，配置換熱器段實現總溫調節。

目前國內超聲速風洞均為暫沖式，代表性的為中國空氣動力研究與發展中心的2 m超聲速風洞。相比暫沖式超聲速風洞，連續式超聲速風洞單次運行時間長，流場參數控制精度高，運行效率高，可在較低速壓下運行，且連續式超聲速風洞啟動/關車時沖擊小，降低了對模型、天平等機構強度的要求。該風洞的建設將填補國內連續式超聲速風洞領域的空白，并通過摸索其運行控制及設計、調試關鍵技術，可為今后更大量級的連續式超聲速風洞的建設調試奠定基礎。

我國第一座跨超聲速風洞是建于1958年的FL-1暫沖式風洞，目前最大的為2 m超聲速暫沖式風洞，其馬赫數范圍1.5～4.0，馬赫數均勻性0.003 3～0.006 2，總壓范圍100～1 200 kPa，總壓控制精度0.3%[1-2]。國外早在1960年就建立了大型連續式超聲速風洞，尺寸最大的為美國阿諾德工程發展中心的16S風洞(建成于1960年)，其口徑達到4.9 m，馬赫數范圍為1.5～4.75(并論證過馬赫數6及以上實施的可能性)，高度模擬范圍為15～45 km[3]。過去幾十年受連續式超聲速風洞建設費用等影響，國內外多以暫沖式風洞建設為主，但最近一二十年，由于連續式超聲速風洞的優異性能以及發展高超聲速武器的緊迫性，又加大了對連續式超聲速風洞的建設投入，比如美國于2013至2015年對封存的16S風洞開展了狀態評估，之后更是進行了耗資6 000萬美元的修復和現代化改造[4-6]。

目前，國內外文獻對連續式超聲速風洞控制系統的設計研究描述極少，即使是關于連續式跨聲速風洞控制系統設計調試的文獻也相對較少[7-15]。美國NTF跨聲速風洞(總壓100～830 kPa，馬赫數0.1～1.2)最近幾年利用二喉道精調來提高馬赫數穩定性；中國空氣動力研究與發展中心的0.6 m連續式跨聲速風洞(下簡稱0.6 m風洞)通過設置內環觀測閾值的串級控制加模糊PID的控制方法，采用轉速粗調加中心體精調的方式，實現馬赫數控制精度達到0.001，并通過分段變參數模糊PID控制算法實現了常壓/增壓下總壓控制精度0.1%(負壓下0.2%)；西北工業大學NF-6跨聲速風洞采用轉速加柵指及其組合的方式實現了馬赫數控制精度0.002。

考慮到連續式超聲速風洞流場建立方式和(低)跨聲速風洞不同，且風洞馬赫數更高，氣動載荷更大，壓縮機功率更高，風洞總壓和馬赫數等參數仍存在相互耦合，因此，如何實現流場參數的精確控制和快速穩定是控制系統設計中的關鍵技術問題。

1 流場參數控制原理

某連續式超聲速風洞啟動運行后，換熱器系統按照一定的冷量運行，即總溫不做精確控制，因此，本文討論的流場參數特指總壓和馬赫數。總壓和馬赫數控制是一個復雜的綜合性任務，需要調動其下屬的各個子系統協調運行，其原理如圖1所示。首先由核心控制器(BOXPC)通過調度噴管/超擴段控制系統調節型面/調節片至對應的馬赫數，然后通過壓縮機控制系統對壓縮機級數以及轉速進行控制來建立風洞運行壓比，并實現馬赫數控制；通過對總壓系統調節閥或真空泵等閉環控制實現總壓的精確調節；通過模型姿態系統實現模型迎角等調節；通過標準參數測量系統實現總壓和馬赫數參數的測量，并作為總壓和馬赫數控制的基準。

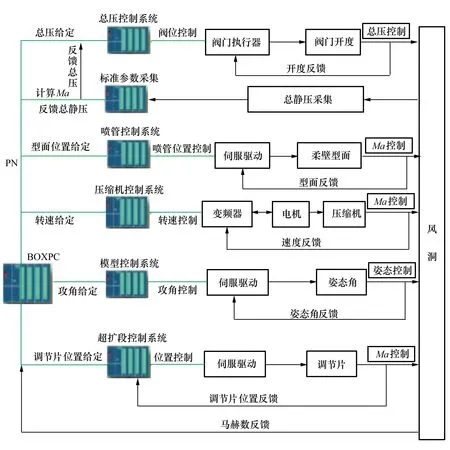
圖1 流場參數控制原理

該風洞總壓的調節手段及影響因素包括：抽真空泵轉速、進氣調節閥開度、排氣/抽氣調節閥開度、氣源壓力和洞體漏氣量；靜壓沒有直接的控制手段；馬赫數的調節手段及影響因素包括：壓縮機轉速、噴管型面、超擴段型面、模型堵塞度等。

連續式風洞馬赫數公式為

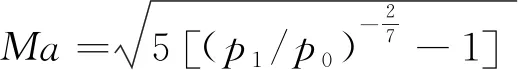
(1)

式中:p0為穩定段總壓;p1為試驗段靜壓。

由公式(1)可知,總壓的調節直接影響馬赫數,而實際中馬赫數調節手段比如壓縮機轉速、半柔壁型面等在調節過程中又將導致總壓的波動,這就導致馬赫數與總壓之間存在耦合,調節難度加大。總壓和馬赫數的耦合關系如圖2所示。

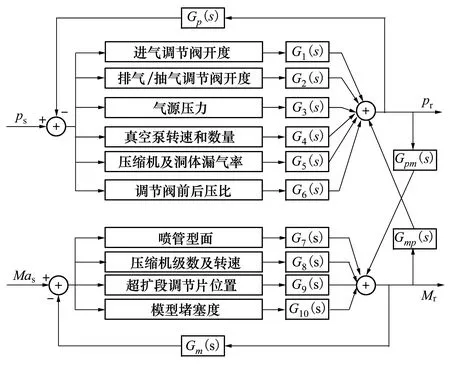
圖2 總壓、馬赫數影響因素及耦合關系

但連續式超聲速風洞和跨聲速風洞的流場參數耦合特性又有所不同。一是馬赫數精確調節方式不同,跨聲速風洞需要通過對中心體/柵指型面、壓縮機轉速等調節手段實時閉環控制來實現馬赫數精確調節,而超聲速風洞主要通過噴管型面、超擴段型面精確調節到位后,利用壓縮機轉速來建立馬赫數流場。另外,兩者在馬赫數和總壓的耦合程度上也不同,超聲速風洞的馬赫數流場主要由壓比決定,當壓比一定時,總壓波動對馬赫數的影響較小;而跨聲速風洞總壓波動時馬赫數波動較大。

由上述分析可知,對于工況復雜、狀態多變的風洞總壓與馬赫數運行流場來說,由于流場參數調節手段多,相互耦合,很難獲得精確數學模型,故而基于數學解耦的現代控制理論難于施行。因此在設計連續式跨聲速風洞流場參數控制方法時,首先基于各自調節手段進行對應參數的閉環控制,同時結合馬赫數與總壓耦合關系,通過技術手段進行解耦來實現流場參數精確控制。

結合流場參數控制原理和耦合關系,擬通過高速網絡設計來實現多調節手段的協調調度,通過高動態高精度的調節/測試手段和先進控制算法來保證流場參數的精確調節和快速穩定。

2 控制系統網路拓撲結構設計

測控系統以嵌入式控制器BoxPC 427E為核心,通過2套智能交換機組建光纖環網,實現風洞的流場控制,并負責對風洞運行相關子系統進行調度和協調控制。各子系統PLC之間采用Profinet RT通信,PLC控制器和伺服驅動器之間采用Profinet IRT進行通信,風洞整體控制調度(包括機構執行)周期控制在100 ms,滿足流場參數控制系統對各調節手段的調度要求。

3 控制系統設計關鍵技術問題

流場參數的精確快速控制除先進的控制算法外還需要考慮時間特性(各機構的響應速度特性能否滿足調度要求)、各執行機構/測試儀器的控制/測試精度能否滿足流場參數控制精度指標、能否保證多變量逐次解耦的及時性,并確保能支撐起控制算法的高效性。

3.1 高精度采集系統設計

由于總壓和馬赫數控制精度要求較高,為保證控制的有效性，需要首先保證流場參數測試的準確性，壓力采集精度對馬赫數偏差的影響可用公式(2)來表示

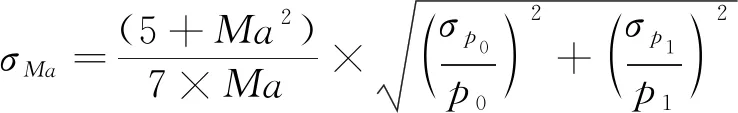
(2)

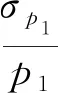
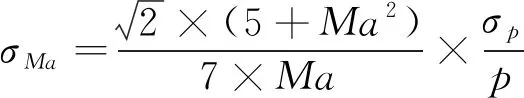
(3)

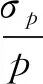
由公式(3)可知當目標馬赫數越低，對壓力采集的精度要求越高，而本風洞啟動馬赫數較高，避免了低馬赫數下對測試儀器高精度的要求。同時，由(1)式得到靜壓隨馬赫數變化情況，如(4)式所示

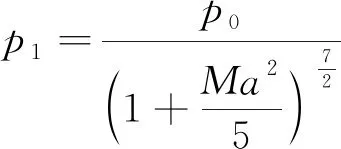
(4)

由(4)式可得到不同穩定段總壓下，馬赫數階梯變化時的靜壓變化，如圖3所示。

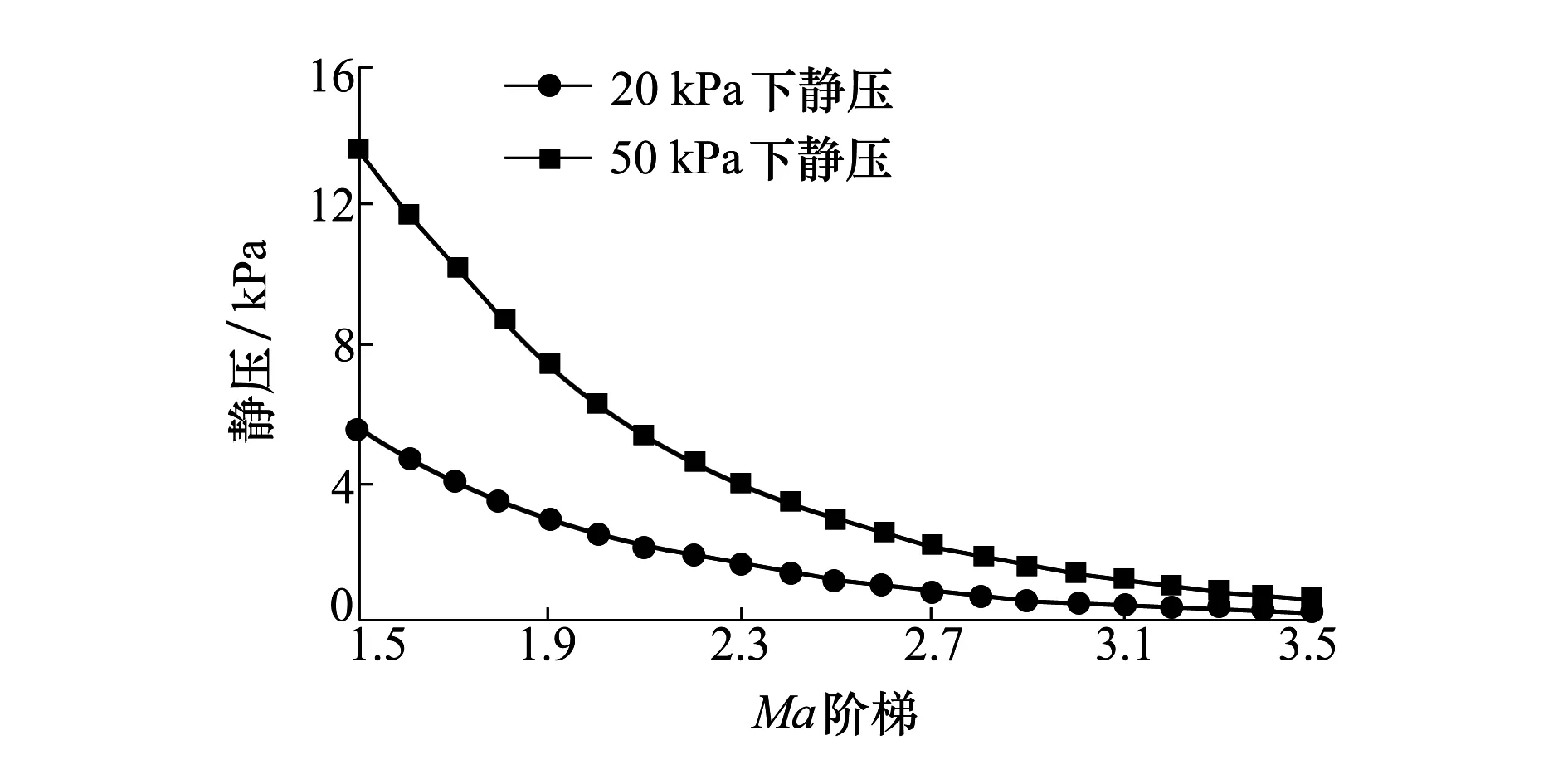
圖3 不同總壓下靜壓隨馬赫數變化情況

由圖3可知，當馬赫數達到3.0時靜壓只有幾百帕，而若要保證總靜壓的精度，結合目前國內外壓力傳感器性能，選取0.02%精度壓力傳感器(其動態響應時間為20 ms)，并采用量程分段的方式以適應不同壓力運行工況的測試需求。

3.2 伺服系統高精度及高動態響應特性設計

作為馬赫數主要調節手段，半柔壁及超擴段等伺服系統需具備較高的定位精度和足夠的動態響應特性,這里重點以柔壁為例來進行描述。半柔壁噴管由上下各6套伺服電動缸驅動，為保證氣流均勻性和柔板不損壞，需要單側6個軸同步運行，上下兩側各6個軸協調運行。柔壁控制系統以1516T-CPU作為控制器，配以Sinamic S120伺服驅動系統實現對半柔壁機構的多軸同步控制。T-CPU接受風洞核心控制器發送的型面控制命令，計算出各推桿運行目標位移，通過S120控制推桿的運動速度。機構上位移傳感器實時采集各推桿的位移，反饋給T-CPU，與設定值不斷比較，并對控制量進行修正，最終形成完整的位置閉環。伺服系統位置定位原理如圖4所示。

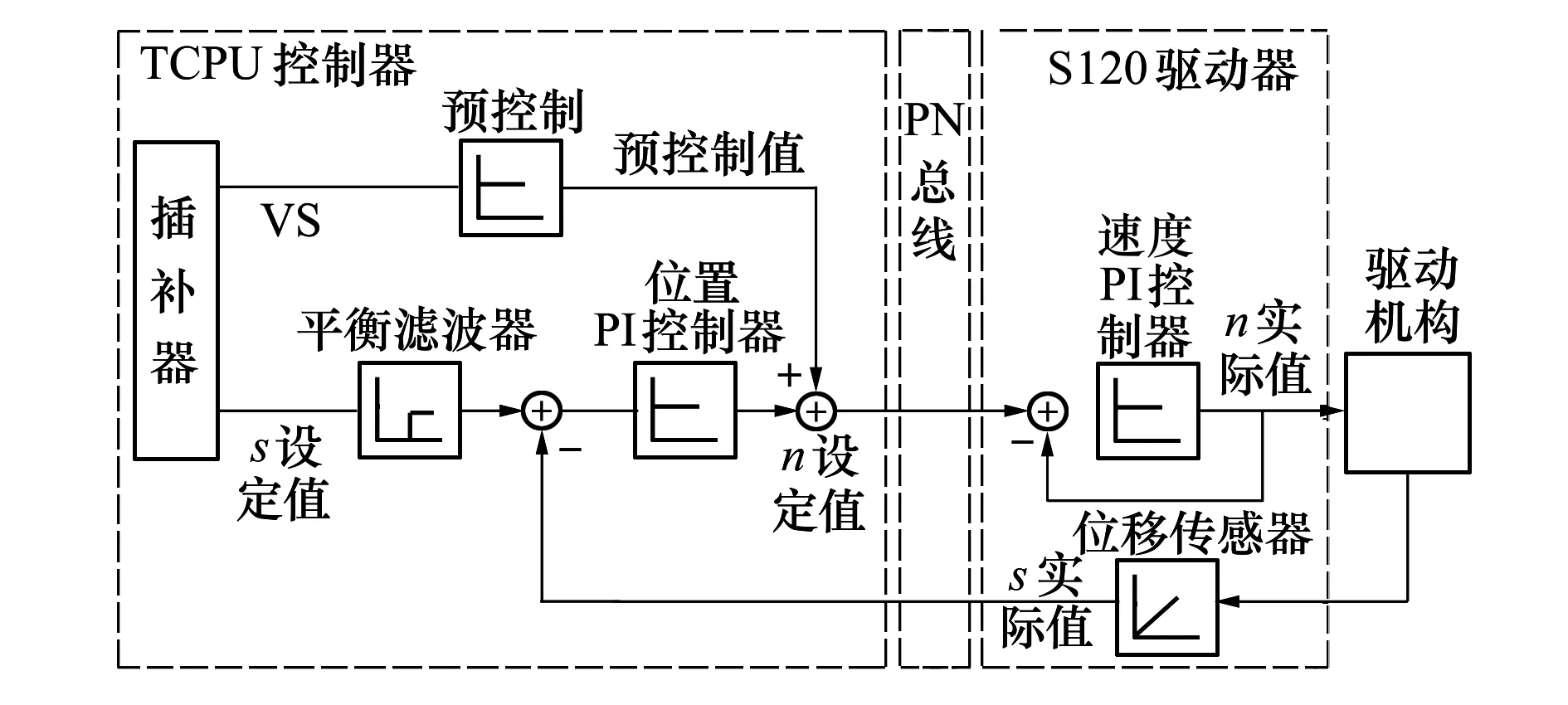
圖4 伺服系統位置定位原理

伺服驅動機構的定位精度d(不考慮機構加工安裝精度)由電機分辨率精度和位移傳感器采集精度兩部分組成，如(5)式(最大誤差)所示

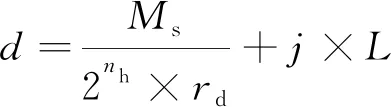
(5)

式中：Ms為推桿絲杠螺距；nh為電機單圈分辨率；rd為電機減速比；j為位移傳感器滿量程精度；L為位移傳感器量程。

在確定機構定位精度要求后，據(5)式可反算各電機、位移傳感器等精度參數。

為保證半柔壁單側6個伺服軸運動過程同步運行，以1號軸為主軸，其他5個軸為從軸，每次運行前先計算各軸的齒輪比

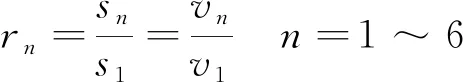
(6)

式中：rn為第n個軸的齒輪比；sn為第n個軸的當次行程；s1為主軸(1號軸)的當次行程；vn為第n個軸的勻速運行速度；v1為1號軸運行速度。

同時，為保證機構運動過程的平穩性，且同起同停，各軸之間應設置可變加速度，且加速度和各軸速度成正比，即

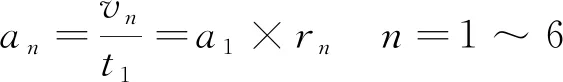
(7)

式中：an為第n個軸加速度；t1為1號軸加速時間，可結合控制器性能和調試需要設置該加速時間。

當前型面運行到位后，再走新的型面時，需重新計算各軸的目標行程，并計算齒輪比和加速度。

TCPU控制系統及伺服驅動系統采用PN-Drive通信協議，總線循環(控制)周期可縮短至3 ms以內。按照s=v×t，當控制周期足夠短，控制器可識別出的各軸之間的不同步量越小，可及早重新對各軸進行位置調度，從而實現更精確的同步控制精度。

3.3 總壓調節手段精度及動態響應特性設計

結合圖2可知，總壓調節手段主要包括調節閥開度、真空泵轉速、氣源壓力等，而氣源壓力受外界影響，不容易控制。這樣，總壓的調節手段變成了真空泵轉速和調節閥開度，而兩者若同時調節，易出現相互耦合。因此，壓力閉環時，真空泵轉速采用前饋控制(不同目標壓力階梯下預置調節)，而利用調節閥進行精調。忽略風洞漏氣，連續式風洞總壓控制精度可參考(8)式[16]：

式中：p為壓力波動量；ps為目標壓力；QVmax為閥門最大體積流量;M為空氣摩爾質量；R1為氣體狀態常數；調節時間為t；x為閥門開度比；R為閥門的可調比；閥門調節過程平均速度為vs；閥門可識別的位置精度(分辨率)為d；s為閥阻比。

考慮到洞體容積較小，只有50 m3，而一般調節閥R=50，同時排氣和抽真空調節閥共用，流量較大(10 min內常壓抽至20 kPa)，結合(8)式，并基于現有市面上調節閥的性能，要求調節閥定位精度優于0.2%，速度(時間)優于25～30 s。

3.4 壓縮機轉速控制精度及動態響應特性設計

壓縮機系統作為動力源，是連續式超聲速風洞最重要的系統，而且壓縮機系統能耗很大，這就對壓縮機的動態特性有很高要求。同時，穩定段總壓和風速的關系如(9)式所示

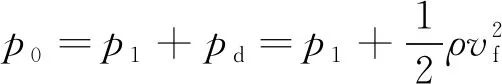
(9)

式中:p0為總壓；p1為靜壓；pd為動壓；ρ為密度；vf為風速。作為馬赫數主要調節手段之一，當壓縮機轉速波動時，(9)式中的靜壓、密度等均會發生變化，進而導致總壓波動。

結合其他連續式跨聲速風洞設計要求(比如0.6 m風洞)和現有壓縮機設計水平，要求壓縮機轉速控制精度達到0.03%，最大升降速度為90 s以內。

4 分段變參數加模糊PI算法實現總壓控制

由于連續式超聲速風洞馬赫數無需主控系統精確調節，在解耦控制時主要考慮馬赫數調節手段對總壓的影響。而在風洞流場參數控制領域，使用較多的算法包括PID控制、模糊控制和預測控制等，考慮到超聲速風洞要建立準確的數學模型很困難，以分段模糊PI控制算法為核心來實施總壓控制。總壓控制策略為：增壓時采用進氣調節閥預置，排氣調節閥精調，負壓時采用進氣調節閥預置，抽氣調節閥加真空泵精調的總壓控制方式。設計時先采用前饋控制方式實施壓力粗調，待壓力進入調節閾值q(t)(設定為目標壓力的96%～104%)后再采用分段變參數加模糊PI控制算法進行總壓精確控制，即在模糊PI的基礎上，首先根據目標總壓調試獲取不同目標壓力下的分段的PI控制參數作為模糊PI基準參數，爾后由模糊算法結合壓力目標和調節閥特性進行變參數控制。其原理框圖如圖5所示。

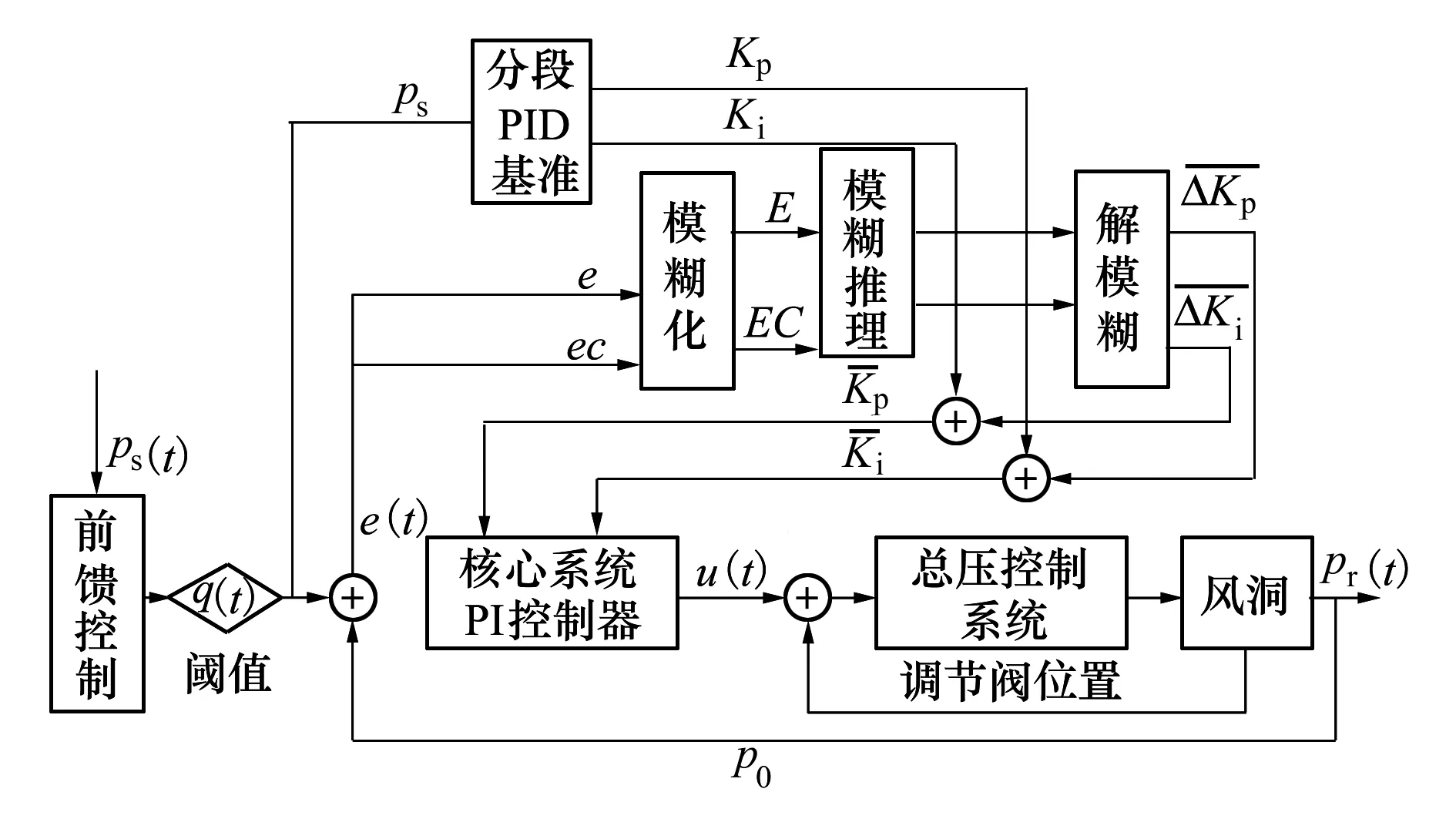
圖5 總壓控制算法調節原理

模糊PI以PI控制器為基礎，PI控制器根據壓力的給定值s(t)和實際值r(t)的偏差e(t)與比例系數Kp、積分時間Ti組合構成控制量輸出，對被控對象進行控制，其控制規律為

(10)

離散化處理后得到(11)式

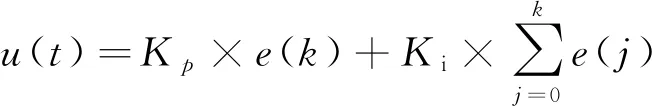
(11)

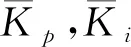
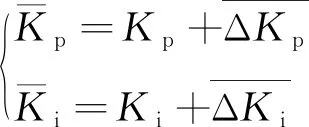
(12)

模糊PI的控制算法描述相對較多，這里就不過多敘述[17-19]。

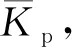
考慮到壓縮機密封氣系統往風洞內漏密封氣(固有特性)，風洞增壓及低真空工況下，需要通過開啟進氣閥進行流量補償，以確保排氣/抽氣調節閥處于合理的調節區間。進入調節閾值q(t)后，進氣調節閥開度V(x)與氣源壓力pa、目標總壓ps滿足(12)式

(13)

同時，負壓工況下真空泵轉速np也隨著(13)式進行預置調節，以防止低真空下抽氣系統流量過大，導致抽氣調節閥進入調節死區。

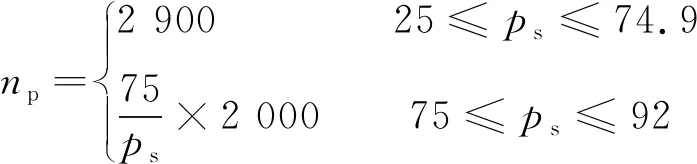
(14)

5 運行控制流程設計及試驗結果

連續式超聲速風洞能耗大，合理優化的運行控制流程是試驗效率優化的前提保證，風洞運行控制主要流程如圖6所示。考慮到馬赫數和總壓的耦合，在啟動或變馬赫數階梯時先利用馬赫數調節手段進行預置，待馬赫數相對穩定后，再利用總壓控制算法實施壓力閉環調節。

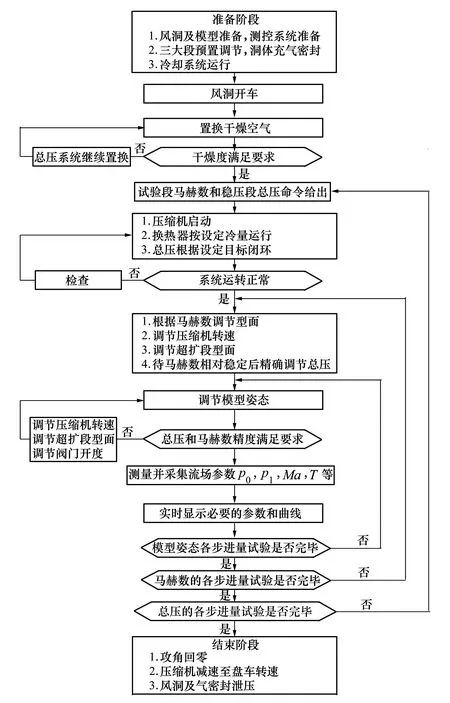
圖6 風洞運行控制流程圖

風洞于2020年開始建設，2021年建設完畢，經過測試，柔壁和超擴段、模型支撐系統機構定位精度優于0.01 mm，同步過程中各軸的不同步量小于0.05 mm。壓縮機轉速控制精度約0.03%。總壓系統調節閥調整為氣驅調節閥，實際定位精度僅為0.5%(分辨率0.5%)，速度為3.2%/s(每秒3.2%的全行程)；受氣驅調節閥死區及動態響應時間影響，調節閥可用調節開度范圍為2%～98%。

風洞吹風結果以2021060201和2021060301 2個典型車次進行描述，試驗條件為變總壓、變馬赫數。馬赫數調節方式為固定壓縮機轉速調節，攻角固定為0°(該風洞目前僅安裝移測架)，流場穩定后采用總壓探針移測架進行移測測試。圖7和圖8分別為20 kPa和60 kPa下變馬赫數測試結果(車次為2021060301)，圖9為100 kPa下變馬赫數測試結果(車次為2021060201)。在噴管運動過程中型面號保持為前一值，只有型面完全成型時，當前型面號才會更新。

從圖7～9中可知，趨穩后壓力控制精度優于0.05%(圖中總壓虛線范圍)，試驗段馬赫數單點穩態控制精度可優于0.000 3(圖中馬赫數虛線范圍)。

由圖7～9中可知，當壓縮機轉速一定時，柔壁型面擴開，馬赫數增大，總壓增大；型面收縮，馬赫數減小，總壓跟隨下降。當壓比達到對應的馬赫數時，馬赫數主要受型面影響，與轉速關系不大。總壓變階梯調節或者當緩慢改變型面或壓縮機轉速時，總壓穩定較快，超調較小；當快速調節型面或大幅調整轉速時會帶來總壓較大幅度的變化(總壓會很快超出精度范圍，如圖中的各尖峰)。

圖7 20 kPa下流場參數測試結果 圖8 60 kPa下流場參數測試結果 圖9 100 kPa時流場參數測試結果

調節馬赫數時(轉速不變)，總壓和馬赫數的穩定時間與馬赫數調節階梯幅度大小、柔壁型面行走時間等相關，平均來看，相鄰2個馬赫數之間總壓穩定時間約20～30 s，馬赫數穩定時間約25～35 s。

部分工況下試驗段馬赫數穩定較慢(如圖7所示高馬赫數)，主要原因是當總壓到達控制精度后，靜壓仍緩慢下降，導致馬赫數穩定存在滯后現象，該現象有可能由以下原因造成，一是該工況下靜壓很低(有時甚至低于1 kPa)，而靜壓傳感器絕對精度僅為12 Pa，測試精度存在一定偏差；二是在對應工況下，試驗段入口側壁處可能存在持續膨脹加速過程，懷疑與風洞壓比建立情況(負壓下壓縮機性能變化)或者負壓下噴管內部流場變動有關。上述現象還有待進一步分析研究。

另外總壓理論上調節精度可以更高，因為風洞用于精調的排/抽調節閥定位精度及分辨率離設計指標有較大差距。

6 結 論

經過試驗驗證可以得出以下結論：

1) 利用本文提出的連續式風洞控制系統設計方法，能夠實現流場指標的精確控制，其中總壓穩態控制精度可達0.05%(設計指標增壓/增壓0.1%，負壓0.2%)，試驗段馬赫數穩態精度優于0.000 3，均達到國軍標先進水平。

2) 本文可為其他連續式超聲速風洞以及大型連續式超聲速風洞的設計調試奠定基礎。

下一步將重點優化試驗效率，包括優化風洞運行流程、優化控制算法并進一步提高流場參數穩定時間，并針對部分工況下馬赫數穩定較慢的問題進行深入研究。