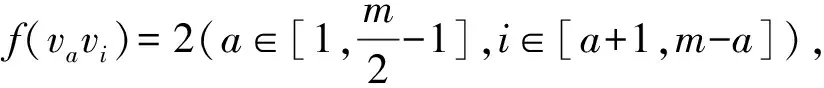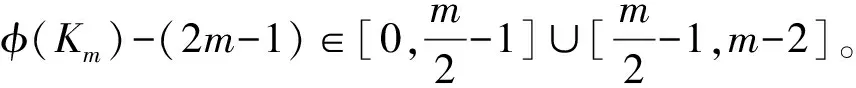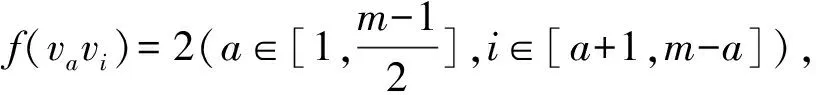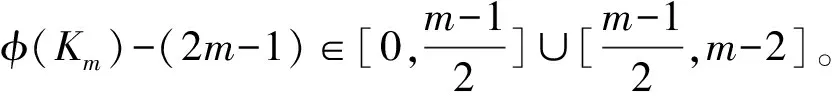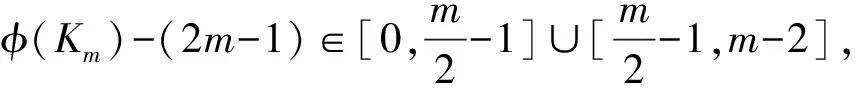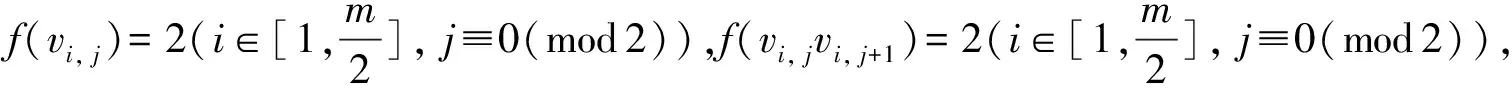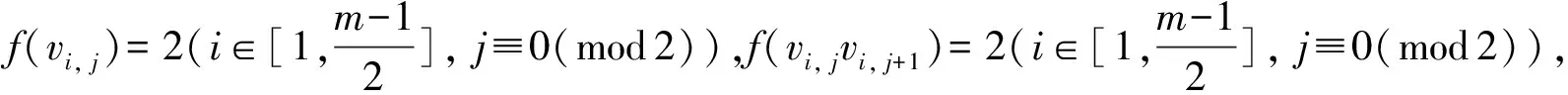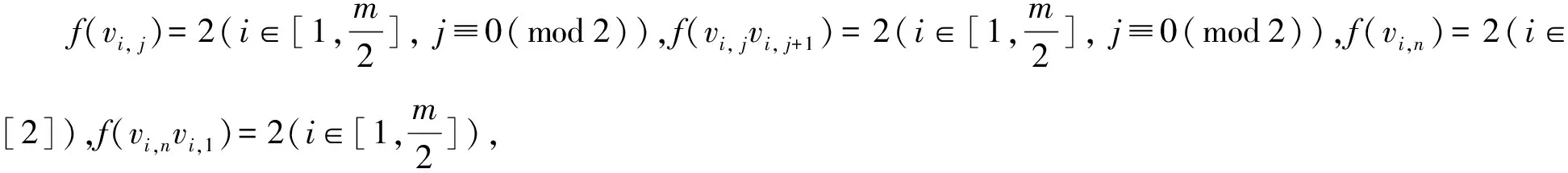幾類笛卡爾乘積圖的鄰點全和可區別全染色
葉宏波, 楊 超*, 殷志祥, 姚 兵
(1.上海工程技術大學 數理與統計學院/智能計算與應用統計研究中心, 上海 201620; 2.西北師范大學 數學與統計學院, 甘肅 蘭州 730070)
0 引 言
圖的染色問題是圖論中的重要問題之一,在數學、化學和計算機科學等領域有廣泛的應用,具體涉及排課問題、交通問題、電路設計問題和無線電通訊頻道分配問題等。從最初的點染色[1]、邊染色[2]和全染色[3-5],再到后來的(鄰)點可區別邊染色[6]、(鄰)點可區別全染色[7-8]、鄰和可區別邊染色[9-10]和鄰和可區別全染色[11-13]等,染色問題一直都是學者們關注和研究的熱點。2017年,Flandrin等[14]定義了圖的鄰點全和可區別全染色,目前此類染色還有待進一步研究。本文將對幾類笛卡爾積圖的鄰點全和可區別全染色問題進行深入探討。
文中V(G)、E(G)和Δ(G)分別表示圖G的頂點集、邊集和頂點的最大度,集合[a,b]={a,a+1,…,b} (a 2021年,Chang等(1)Chang J Z, Yang C, Yin Z X, et al. Neighbor full sum distinguishing non-proper total coloring of graphs[J]. Submitted to Journal, 2021.研究了路、圈、三正則圖、星、完全圖、超立方圖、二部圖、完全r-部圖的鄰點全和可區別全染色,并提出下述猜想: 猜想[15]: 對于任意一個階數至少為3的簡單連通圖G,都有fgndi∑(G)≤3。 定義2設G1=(V1,E1)與G2=(V2,E2)是2個簡單連通圖,G1與G2的笛卡爾乘積圖定義為G1×G2=(V,E),其中,V=V1×V2={(ui,vj)|ui∈V1,vj∈V2}, E={((u1,v1), (u2,v2))|v1=v2且(u1,u2)∈E1,或u1=u2且(v1,v2)∈E2}。 本文研究了幾類笛卡爾乘積圖的鄰點全和可區別非正常全染色,所得結論證實了上述猜想。 本文中路、圈之間的笛卡爾乘積圖分為:①路與路笛卡爾乘積圖;②路與圈笛卡爾乘積圖;③圈與圈笛卡爾乘積圖。本文定義Gm×Hn表示有m行和n列,其中,vi, j表示第i行第j列的點。 定理1fgndi∑(Pm×Pn)=2。 證明易得fgndi∑(P2×P2)=2。由于m為奇數,n為偶數,與m為偶數,n為奇數時Pm×Pn結構相同,所以下面分3種情況討論。 情形1.m≡1(mod 2),n≡1(mod 2)。 首先令f(vi, j)=2(i≡0(mod 2),j≡0(mod 2)),其余點和邊均染1。 此時各點的權重為:φ(v1,1)=φ(v1,n)=φ(vm,1)=φ(vm,n)=5; φ(vi, j)=8(i=1,m,j≡0(mod 2);i≡0(mod 2),j=1,n); φ(vi, j)=7(i=1,m,j≡1(mod 2),j≠1,n;i≡1(mod 2),i≠1,m,j=1,n); φ(vi, j)=9(i≡1(mod 2),i≠1,m,j≡1(mod 2),j≠1,n); φ(vi, j)=10(i≡0(mod 2),j≡0(mod 2)); φ(vi, j)=11(i≡0(mod 2),j≡1(mod 2),j≠1,n;i≡1(mod 2),i≠1,m,j≡0(mod 2))。 情形2.m≡0(mod 2),n≡0(mod 2)。 令f(vi, j)=2(i≡0(mod 2),i≠m,j≡0(mod 2),j≠n),f(vm-1, jvm, j)=f(vi,n-1vi,n)=2 (i≡0(mod 2),i≠m,j≡0(mod 2),j≠n),其余點和邊均染1。 此時各點權重為:φ(v1,1)=φ(v1,n)=φ(vm,1)=φ(vm,n)=5; φ(vi, j)=7(i=1,m,j≡1(mod 2),j≠1;i≡1(mod 2),i≠1,j=1,n); φ(vi, j)=8(i=1,m,j≡0(mod 2),j≠n;i≡0(mod 2),i≠m,j=1,n); φ(vi, j)=9(i≡1(mod 2),i≠1,j≡1(mod 2),j≠1); φ(vi, j)=10(i≡0(mod 2),i≠m,j≡0(mod 2),j≠n); φ(vi, j)=11(i≡0(mod 2),i≠m,j≡1(mod 2),j≠1;i≡1(mod 2),i≠1,j≡0(mod 2),j≠n)。 情形3.m≡0(mod 2),n≡1(mod 2)。 此時令f(vi, j)=2(i≡0(mod 2),i≠m,j≡0(mod 2)),f(vm-1, jvm, j)=2(j≡0(mod 2)),其余點和邊均染1。 則各點的權重為:φ(v1,1)=φ(vm,1)=φ(v1,n)=φ(vm,n)=5; φ(vi, j)=8(i=1,m,j≡0(mod 2);i≡0(mod 2),i≠m,j≡0(mod 2)); φ(vi, j)=7(i=1,m,j≡1(mod 2),j≠1,n;i≡1(mod 2),i≠1,j=1,n); φ(vi, j)=9(i≡1(mod 2),i≠1,j≡1(mod 2),j≠1,n); φ(vi, j)=10(i≡0(mod 2),i≠m,j≡0(mod 2)); φ(vi, j)=11(i≡0(mod 2),i≠n,j≡1(mod 2),j≠1;i≡1(mod 2),i≠1,m,j≡0(mod 2))。 綜上3種情形可得任意相鄰兩點的權重各不相等,即fgndi∑(Pm×Pn)≤2,又fgndi∑(Pm×Pn)≥2,所以fgndi∑(Pm×Pn)=2。 定理2fgndi∑(Pm×Cn)=2。 證明以下分4種情形進行討論。 情形1.m≡0(mod 2),n≡1(mod 2)。 此時令f(vi, j)=2(i≡0(mod 2),j≡0(mod 2)),其余點和邊均染1。 則各點的權重為:φ(vi, j)=7(i≡1(mod 2),j=1,n); φ(vi, j)=8(i≡0(mod 2),j=1,n); φ(vi, j)=9(i≡1(mod 2),j≡1(mod 2),j≠1,n); φ(vi, j)=10(i≡0(mod 2),j≡0(mod 2)); φ(vi, j)=11(i≡1(mod 2),j≡0(mod 2);i≡0(mod 2),j≡1(mod 2),j≠1,n)。 情形2.m≡1(mod 2),n≡1(mod 2)。 由于m-3≡0(mod 2),所以可令f(vi, j)=2(i≡1(mod 2),i>3,j≡0(mod 2)), f(e0)=f(v0)=1(e0∈E(G1),v0∈V(G1){vi, j}),其中(G1=Pk×Pn,k∈[4,m]); f(v1, jvm, j)=1。f(v1, jv1, j+1)=2(j≠n);f(v1, jv2, j)=2;f(v3, j)=2(j≡0(mod 2)); f(v2, jv3, j)=f(v3, jv4, j)=2(j≡0(mod 2));f(v3, jv3, j+1)=2(j≡0(mod 2),j≠2); f(v3,1v3,2)=2;f(e1)=f(v1)=1(e1∈E(G)E0,v1∈V(G)V0)(E0表示上述已染色的邊集,V0表示上述已染色的點集)。 此時,各點的權重為:φ(u)(u∈V(G1){v4, j})同情形1,其余點的權重如下: φ(v4,1)=φ(v4,n)=7;φ(v2,1)=φ(v2,n)=8;φ(vi, j)=9(i=1,3,j=1,n); φ(v4, j)=9(j≡1(mod 2),j≠1,n);φ(v2, j)=10(j≡1(mod 2),j≠1,n); φ(v2,3)=11;φ(vi, j)=13(i=1,3,j≡0(mod 2)); φ(vi, j)=12(i=1,j≡1(mod 1),j≠1,n;i=2,4,j≡0(mod 2);i=3,j≡1(mod 2),j≠1,3,n) 情形3.m≡0(mod 2),n≡0(mod 2)。 f(vi, j)=2(i≡0(mod 2),j≡0(mod 2),j≠n);f(vi,n-1vi,n)=2(i≡0(mod 2)); f(e2)=f(v2)=1(e2∈E(G)E1,v2∈V(G)V1)(E1表示上述已染色的邊集,V1表示上述已染色的點集)。此時各點的權重如下: φ(vi, j)=7(i≡1(mod 2),j=1,n);φ(vi, j)=8(i≡0(mod 2),j=1,n); φ(vi, j)=9(i≡1(mod 2),i≠1,j≡1(mod 2),j≠1); φ(vi, j)=10(i≡0(mod 2),j≡0(mod 2),j≠n); φ(vi, j)=11(i≡1(mod 2),j≡0(mod 2),j≠n;i≡0(mod 2),j≡1(mod 2),j≠1)。 情形4.m≡1(mod 2),n≡0(mod 2)。 f(vi, j)=2(i≡1(mod 2),i≠1,j≡0(mod 2),j≠n);f(vi,n-1vi,n)=2(i≡1(mod 2),i≠1); f(v1,1)=f(v1,n)=f(v1, jv1, j+1)=2(j≠n);f(v1, jv2, j)=2。其余點和邊均染色1。 則各點的權重為:φ(vi, j)=7(i≡0(mod 2),i≠2,j=1,n); φ(vi, j)=8(i≡1(mod 2),i≠1,m,j=1,n); φ(vi, j)=9(i=2,m-1,j=1,n;i≡0(mod 2),i≠2,j≡1(mod 2),j≠1); φ(vi, j)=10(i=1,j=1,n;i≡1(mod 2),i≠1,j≡0(mod 2),j≠n;i=2,j≡1(mod 2),j≠1); φ(vi, j)=11(i≡0(mod 2),j≡0(mod 2),j≠n;i≡1(mod 2),i≠1,j≡1(mod 2),j≠1); φ(vi, j)=12(i=1,j≡1(mod 2),j≠1,n-1); φ(vi, j)=13(i=1,j≡0(mod 2),j≠2,n); φ(vi, j)=14(i=1,j=2,n-1)。 由上述4種情形可得任意相鄰兩點的權重各不相等,即fgndi∑(Pm×Cn)≤2, 又fgndi∑(Pm×Cn)≤2,因此,fgndi∑(Pm×Cn)=2。 定理3fgndi∑(Cm×Cn)=2(m,n>6)。 證明由于Cm×Cn在m、n分別為奇數和偶數的結構與m、n分別為偶數和奇數時相同,故以下考慮3種情況即可。 情形1.m≡0(mod 2),n≡0(mod 2)。 令f(vi, j)=2(i≡1(mod 2),j≡0(mod 2)),其余點和邊均染1。 則各點的權重為:φ(vi, j)=9(i≡0(mod 2),j≡1(mod 2)); φ(vi, j)=10(i≡1(mod 2),j≡0(mod 2)); φ(vi, j)=11(i≡1(mod 1),j≡1(mod 2);i≡0(mod 2),j≡0(mod 2))。 情形2.m≡0(mod 2),n≡1(mod 2)。 令f(vi, j)=2(i≡1(mod 2),j≡1(mod 2));f(vi,nvi,1)=2(i≡1(mod 2)); f(vi,1vi,2)=2(i≡1(mod 2));f(vi,1vi+1,1)=2(i≡1(mod 2));其它均為1。 則各點的權重為:φ(vi, j)=9(i≡0(mod 2),j≡0(mod 2)); φ(vi, j)=10(i≡1(mod 2),j≡1(mod 2),j≠1,n); φ(vi, j)=11(i≡1(mod 2),j≡0(mod 2),j≠2;i≡0(mod 2),j≡1(mod 2),j≠1); φ(vi, j)=12(i≡1(mod 2),j=2,n;i≡0(mod 2),j=1); φ(vi, j)=14(i≡1(mod 2),j=1)。 情形3.m≡1(mod 2),n≡1(mod 2)(m>6,n>6)。 令f(vi, j)=2(i≡1(mod 2),j≡1(mod 2),(i≠m,j≠1)); f(vi,nvi,1)=2(i≡1(mod 2),i≠m);f(vi,1vi,2)=2(i≡1(mod 2)); f(vi,1vi+1,1)=2(i≡1(mod 2),i≠m);f(vm, jv1, j)=2(j≡1(mod 2),j≠n); f(vm-1, jvm, j)=2(j≡1(mod 2),j≠n); f(vm, jvm, j+1)=2(j≡1(mod 2),j≠n;j=4,m-1);f(v1,3v1,4)=2; f(v1,5v2,5)=2;其余點和邊均為1。 則各點的權重為:φ(vi, j)=9(i≡0(mod 2),j≡0(mod 2)); φ(vi, j)=10(i≡1(mod 2),i≠1,m,j≡1(mod 2),j≠1,n); φ(vi, j)=13(i=1,j=3,5,n;i=m,j=4,n-2); φ(vi, j)=14(i=m,j≡1(mod 2),j≠n,i≡1(mod 2),i≠1,j=1);φ(v1,1)=15。 因此,fgndi∑(Cm×Cn)≤2又fgndi∑(Cm×Cn)≥2,即證fgndi∑(Cm×Cn)=2。 定理4fgndi∑(Km)=3。 證明由完全圖Km的定義知,Km的一個鄰點全和可區別全染色實則為一個鄰和可區別邊染色。若Km只用2種顏色處理,不妨將點都染1,一個點對剩下(m-1)個點有(m-1)條連邊,則每個點的關聯邊染2的個數范圍只可能為[0,m-1],若存在(m-1)條關聯邊都染2的點u,一定存在(m-1)條關聯邊全染1的點v,由于u,v相鄰,故不存在上述情形,即Km無法用2種顏色來區分。φ(Km)表示完全圖Km中各點權重的集合。若Km只用2種顏色染色,同時達到權重相同的點只有2個,染色情況如下: 情形1.m≡0(mod 2)。 情形2.m≡1(mod 2)。 若用3種顏色,則對于上述2種情形做出如下調整: 情形2.1.m≡0(mod 4)。 此時φ(Km)-(2m-1)∈[0,m-1]。 情形2.2.m≡2(mod 4)。 情形2.3.m≡1(mod 4)。 此時φ(Km)-(2m-1)∈[0,m-1]。 情形2.4.m≡3(mod 4)。 由上述情形可知:fgndi∑(Km)≤3,又fgndi∑(Km)≥3,即證fgndi∑(Km)=3。 定理5fgndi∑(Pn×Km)=2(m>5,n≥2)。 情形1.m≡0(mod 2),n≡0(mod 2)。 情形2.m≡0(mod 2),n≡1(mod 2)。 情形3.m≡1(mod 2),n≡0(mod 2)。 情形4.m≡1(mod 2),n≡1(mod 2)。 由上述情況可得fgndi∑(Pn×Km)≤2(m>5,n≥3),又fgndi∑(Pn×Km)≥2。即證fgndi∑(Pn×Km)=2(m>5,n≥3)。 定理6fgndi∑(Cn×Km)=2(m>5,n≥3)。 證明分析同定理5。下面分3種情況進行討論。 情形1.n≡0(mod 2)。 情形2.n≡1(mod 2),m≡0(mod 2)。 情形3.n≡1(mod 2),m≡1(mod 2)。 由上述3種情況可得,fgndi∑(Cn×Km)≤2(m>5,n≥3)。 又fgndi∑(Cn×Km)≥2,即證fgndi∑(Cn×Km)=2(m>5,n≥3)。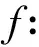
1 路、圈之間的笛卡爾乘積圖
2 路、圈分別與完全圖的笛卡爾乘積圖