基于A星算法的無人機高速公路巡檢應用研究

靳 朝,林富生,宋志峰,余聯慶

(武漢紡織大學 機械工程與自動化學院,湖北 武漢 430200)

0 引言

目前,國內高速公路巡檢主要是人工巡檢和固定式路測監控設備巡檢兩種巡檢方式:人工巡檢費時費力,效率低下且巡檢工作人員有安全風險;固定式路測監控設備僅分布在個別重要路段,數量有限[1-3]。此兩種巡檢方法的低效率、高支出,難以應對復雜地形及惡劣環境,缺乏即時反饋手段,已經難以滿足日益加重的高速公路巡檢任務。對此,無人機技術作為一種新型技術可以擺脫上述困難,降低環境因素所造成的影響,保證巡查的效率與便捷。

1 無人機航跡規劃的實現原理

無人機的航跡規劃主要分為4個部分:初始化參數、構建地圖、路徑搜索、路徑優化,如圖1所示。

圖1 無人機航跡規劃技術流程

1.1 參數初始化

在進行無人機自主飛行航跡規劃之前需要對無人機進行結構分析和數據估算來確定無人機的約束條件,其約束條件包括最大爬升角、最小步長等。無人機的最大爬升角指無人機的航跡坐標系X軸與水平面之間所能形成的最大夾角,最大爬升角影響的是無人機三維空間的節點劃分距離,每一個三維立體節點之間所形成的爬升角必須要小于無人機的最大爬升角。無人機的最小步長是指在當前飛行環境中無人機改變飛行狀態所需要飛行的最小直線距離,無人機的最小步長影響的是無人機二維空間的節點劃分距離,二維節點間的最短距離不得小于無人機的最小步長。為了簡化空間模型,將三維的空間轉化為二維空間,消除無人機最大爬升角的約束,所有避障方式全部選擇繞飛。

1.2 構建地圖

因為采用繞飛的避障策略,所有Z軸方向上的障礙物都可以投影在俯視的XY平面上,在進行空間模型簡化后,得到的就是一張二維的空間分布圖。為了更加精確地模擬無人機的飛行,使用柵格法構建了一個30 m×30 m的二維空間地圖;再根據無人機本身的俯視投影面積大小,來確定無人機的工作區間大小,以確保無人機有足夠的飛行空間。

1.3 路徑搜索

路徑搜索的基本原理就是通過將所需飛行區域簡化為方形柵格,方形柵格也就成為了一個二維數組,每一個柵格就是二維數組的一個元素,而這些元素都帶有標記,每一個元素都是一個節點,每一個節點都帶有可到達或不可到達的標識。在設定好起始點和目標點后,無人機會根據自身所帶的攝像模塊識別每一個節點所攜帶的標識,最終再串聯帶有可到達標識的節點,形成一條路徑最終到達目標點。

2 基于A?(A星)算法的航跡路徑規劃無人機

A?航跡搜尋算法是一種作用于搜索區域的啟發式算法[4],A?航跡搜索算法結合于Dijkstra算法和BFS算法,所以它兼具兩種算法的優點,不僅能夠搜索到最短路徑,而且可以使用啟發函數。A?航跡搜尋算法在規劃航跡時會對每一個節點進行估值,即:

式中:F(n)指最后經過n個節點所得到的路徑;G(n)指從起點出發到達第n個節點所付出的移動代價;H(n)指從第n個節點到達目標點的估算成本。

從起點開始A?算法會建立一個庫,這個庫被稱為open list。open list作為一個待檢查的清單,從起點開始每一個經過的節點周圍的所有可到達節點都會進入這個庫,反復遍歷open list查找F(n)最小值的點,再把它當做處理點,將周圍的可到達節點納入open list,這個處理點會被納入另一個庫close list,當節點進入close list后就不會再被當做處理點,重復上述過程,一直到把目標點納入open list,即得到一條最優的路徑,如圖2所示。

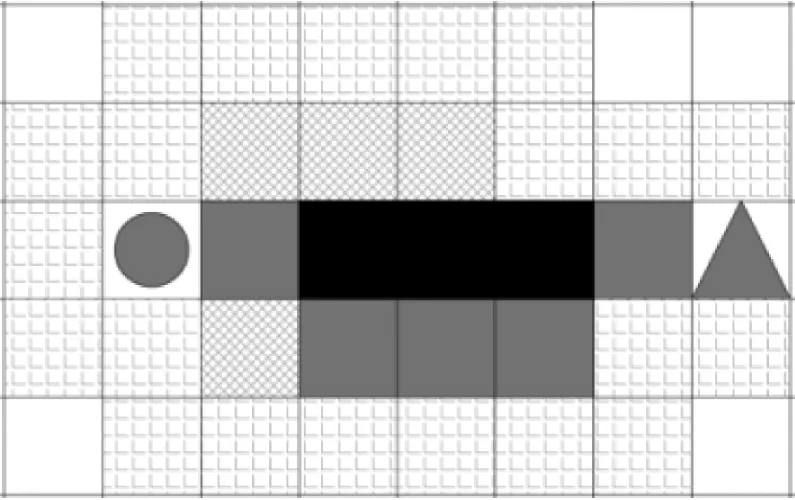
圖2 A?算法示意圖

圖2中,灰色圓點代表起點,灰色三角形代表終點,黑色填充方格代表障礙物,小方塊填充方格代表待搜索的open list,交叉線填充方格代表已經搜索過的close list,灰色填充方格代表當前搜索過的路徑。

得到路徑的過程即估算成本取決于H(n)所使用的啟發函數,本文使用的是曼哈頓算法和歐幾里得啟發算式。

曼哈頓啟發函數為:

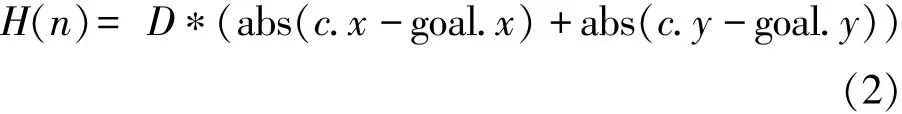
式中:D表示一個柵格的曼哈頓距離;c代表當前節點;goal代表目標節點。

歐幾里得啟發函數為:

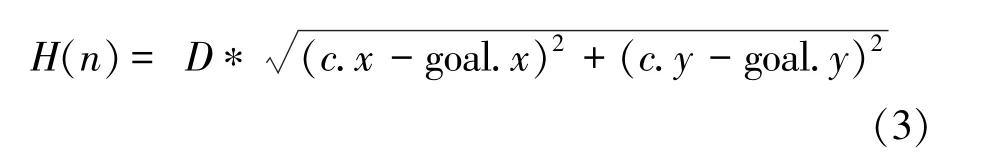
式中:D表示一個柵格的歐幾里得距離;c代表當前節點;goal代表目標節點。

因為歐幾里得距離接近兩點最短距離,所以得到的路徑為最短距離,同時結合曼哈頓啟發算法,可以保證路徑的穩定性,計算后得到最優航跡路線。

3 基于A?算法的無人機仿真實驗

3.1 環境構建與運行仿真

為了保障算法可以應用于大多數復雜場景下,在模擬場景中將會盡量多地構建不同類型的障礙物。根據無人機的最小步長,將模擬空間平面圖構建為一個30 m×30 m的地圖,每一個無人機無法到達的障礙點都用一個黑色柵格表示,其他無標注區域均為無人機可活動區域,灰色圓點代表無人機所在位置,灰色三角形代表無人機的目標點,如圖3所示。通過運用卡爾曼數據融合技術對各傳感器的各項數據進行整合,然后解算無人機的姿態。再運用曼哈頓距離的啟發算法對G(n)進行推算,同時通過路徑的改變不斷地計算出各點的F(n),確保無人機沿G(n)最小值的路徑進行移動,最終得出最短路徑,如圖3所示。

3.2 路徑優化

如果通過A?路徑算法搜索所得到的最優航跡路線是一條直線,那么就不用對所得航跡進行路徑優化處理。但是在現實環境中飛行航跡不會這么理想化,因此需要對航跡進行平滑處理,而要進行平滑處理就需要消除無人機最大升角和最小步長的影響。本文使用Savitzky-Golay濾波(SG濾波),SG濾波[5]基于局域多項式最小二乘法擬合的濾波方法,其擬合多項式為:

式中:p(n)為擬合多項式;ak為第k個數值;k為數據項數。

其最小二乘殘差為:

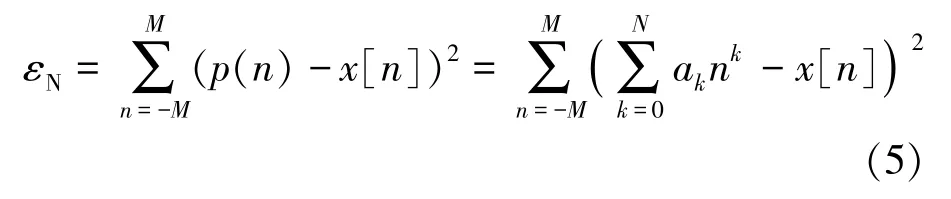
式中:εN為殘差期望值;x[n]為給定模型函數。

其運算可以通過卷積運算的方式實現,算式如下:

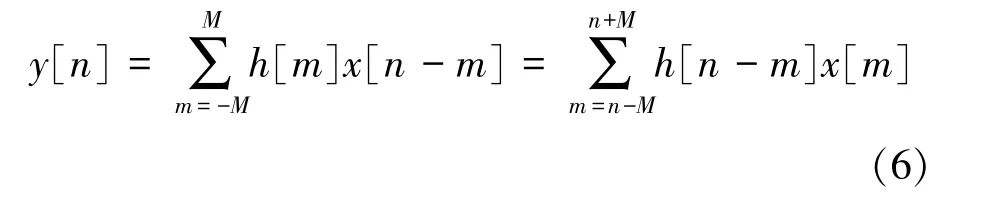
式中:y[n]為濾波后的結果信號;h[n]為濾波系數;x[n]為輸入信號;M表示濾波的抽頭數;濾波階數為M-1。

再將所得航跡路線進行平滑處理后得到的路徑如圖4所示。

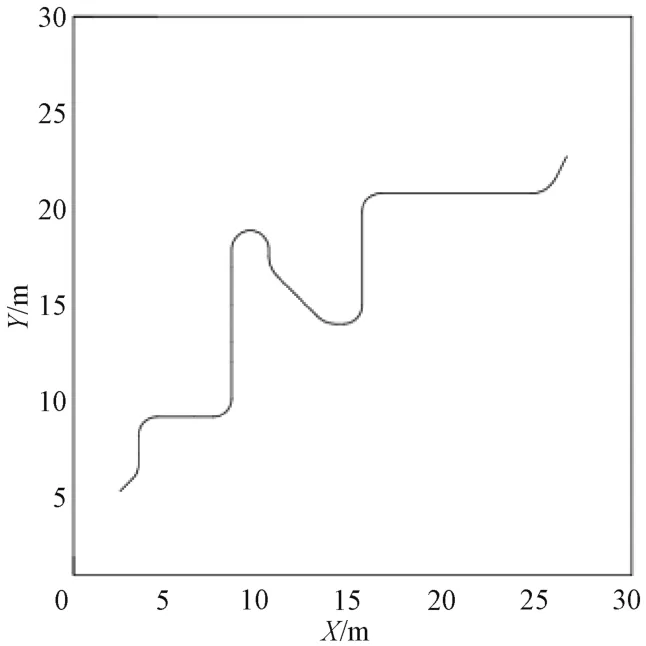
圖4 平滑處理后的航跡路線簡化圖

由圖4可以看出,由于對飛行航跡路線進行了優化處理,更加地符合無人機的飛行運動規律,同時因為對每一個轉角的平滑處理使得無人機在貼近障礙物飛行時不會因為轉折角度問題貼近障礙物的邊緣,故以此種尋跡方法進行飛行會降低無人機飛行的碰撞危險性。

4 結語

從上述實驗可以看出,基于A?算法的無人機在較為復雜的環境中可以實現尋跡、避障等操作。針對基于傳統人工的巡查方式,本文通過分析高速公路的環境特征、巡查特點,結合無人機技術,對無人機在高速公路巡查的應用進行研究,提出無人機自主飛行高速公路巡查方案。