回顧與反思，促進深度學習的利器

鄭俊智

(福建省廈門市海滄區霞陽小學 福建 廈門 361000)

古今中外不少大家都推崇反思的重要性：荷蘭著名數學家費賴登塔爾教授指出:“反思是數學思維活動的核心和動力”，在《數學新課程標準》中更是明確指出“要使學生形成反思的意識和能力”。而人教版小學數學教材中“解決問題”的最后一個環節是就是“回顧與反思”，它在整節課所占的比重雖不大，但是卻起到畫龍點睛的作用。而對于時下流行的深度學習的理念，學者何玲、黎家厚認為，教學中的深度學習是指學習者能將新知識和思想融入原有的認知結構中，在眾多思想中進行聯系，并將已有的知識遷移到新的情境中。這種學習方法注重的是學生對新知識進行批判性地分析，將新舊知識進行聯系，是一種有思維深度的學習方法。“回顧與反思”環節恰恰契合了深度學習的理論要求，它既梳理整合前后知識，又培養學生運用多樣方法進行反思，讓學生經歷解決問題的過程，對培養學生的發散思維，構筑完整的“解決問題”模型有著不可或缺的作用。然而，我們的課堂上卻時常忽略了這個環節的巨大價值，主要體現在以下兩個方面：

(1)只關注檢驗的結果，忽視反思的過程。不少教師在“回顧與反思”環節中經常強調的是檢驗的結果是否有誤，殊不知檢驗只是這個環節其中的一個目的，而反思才是引導學生建立解決某一類問題的一般方法，梳理數學思想，構建問題模型的關鍵，回顧與反思不應僅僅與驗算劃上等號。

(2)只關注檢驗的速度，忽視方法的多樣性。很多教師舍不得在這一環節花費太多時間，所以往往選擇單一、機械的檢驗方法，比如把算式重頭到尾再重新計算一遍，或者把得數當成已知數，代入題目當中，按照題目的意思倒著計算，看結果是不是符合題目的已知條件。漸漸地，學生只會套用這樣的檢驗模式，“回顧與反思”在學生眼中儼然成為一種枯燥的、可有可無的過場。

這些情況我們常常忽視了，但是細究起來，回顧與反思卻是每節課必備的環節，如果利用得好，知識的脈絡會在學生腦海中清晰地再現，對新課部分掌握的不是很到位的孩子還能再經歷一次知識梳理和回顧，無疑能提高知識的接受程度和作業的正確率，達到深度學習的良好效果。那么，教師該如何轉變才能發揮“回顧與反思”對深度學習的重要作用呢？筆者嘗試從以下幾個方面進行轉變：

1.回顧過程，聚焦數學本質，促進深度理解

當一節新課接近尾聲的時候，回顧整個新課的知識脈絡，常常會發現，《解決問題》這一課與本單元的知識體系是一脈相承的，它是本單元所承載的數學本質的延伸和運用，并非獨立的知識點，如果教師能在課末組織學生將一節課的探究過程進行梳理和回顧，著重聚焦本單元所要滲透的數學本質，勢必引發學生對《解決問題》的所蘊含數學思想的深刻理解。

以人教版三年級下冊第五單元《面積》的解決問題《鋪磚問題》為例：“正方形地磚的邊長是3分米，客廳的長是6米，寬是3米。鋪客廳地面一共要用多少塊地磚？”這道題涉及到兩種方法：

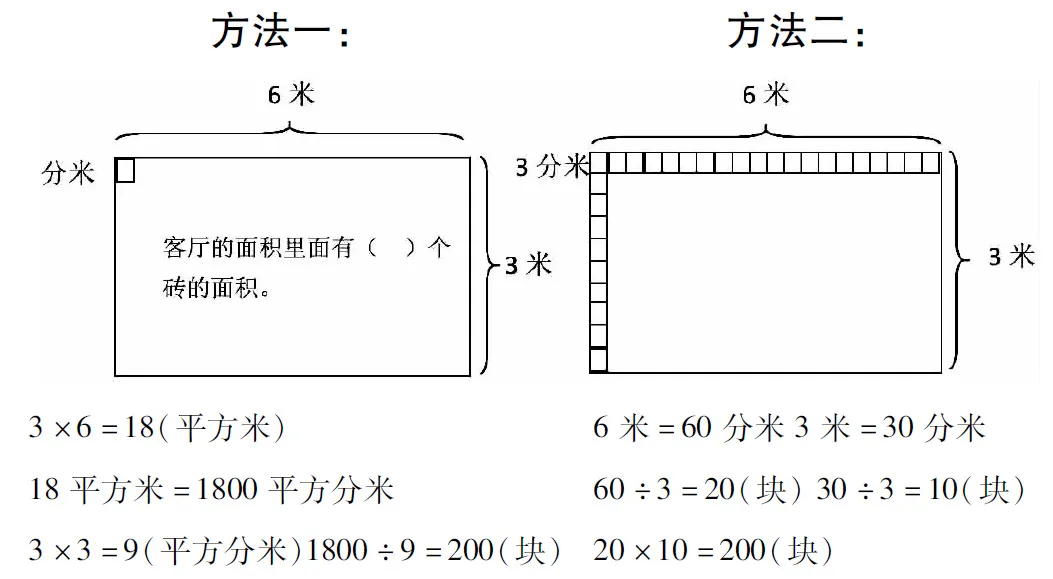
方法一是分別計算出一塊磚的面積和客廳的面積，再用客廳的面積除以磚的面積，求出客廳的面積里面含有幾塊磚的面積，計算得出需要200塊地磚。方法二是分別求出客廳的長和寬分別能鋪出幾塊磚，再把兩個數據相乘。在回顧與反思環節，老師引導學生跟著教材的建議進行檢驗：“9×200=1800(平方分米)，1800平方分米=18平方米，正好與客廳的面積相等，解答正確。”此時，教師若能進一步梳理鋪磚問題的過程則比檢驗來得更有意義，可以把這節課的過程和《長方體、正方體面積的計算》進行類比，引導學生發現原來鋪磚問題的本質和長方體、正方體的面積的探索過程類似，都是求有幾個這樣的面積單位，所不同的是這里是把一塊磚看成面積單位。為什么我們求面積的時候不用再除以面積單位呢，因為常見面積單位對應的值是1，比如長5米，寬4米的長方形面積是5×4=20(平方米)，20再除以1就顯得畫蛇添足了。而方法二就和長方形面積的推導過程十分相似了，先求出一列的面積單位數量，再求出一行面積單位的數量，再把兩者相乘。

通過這樣的類比和梳理，把前后知識點融會貫通，找到原本知識的生長點和聯系點，利用舊知解決新知。在這過程中，學生發現課與課之間的聯系并不是完全割裂的，而是“連筋帶骨”的，并學會了舉一反三，靈活應用，對方法掌握更為透徹，對本質的認識更為深刻。

2.反思方法，感受多元策略，引發深度思考

方法多樣化一直是數學課程推崇的，它能幫助孩子打開思路，體現的是孩子們對同一個問題的不同理解水平。在新授課的環節，我們常常鼓勵孩子在探究中采用不同的解決方法，但是反思檢驗的環節花的力氣并不多，常常是一筆帶過。最常使用的檢驗方法就是將計算結果代入題目當中看能否反推出題目的已知條件，一提到檢驗，孩子們腦海里呈現的大都是這種方法，這樣的思維定勢限制了學生思維的發散，其實如果在反思檢驗的環節，教師也能尊重孩子的不同思維水平，鼓勵方法的多樣化，在對比與優化中感受多元的策略，那么孩子的思路就會進一步打開，反思就不止停留在淺層上，從而引發更深度的思考。

以三年級下冊第三單元《測量》例9《乘船問題》為例，題目是這樣的：下面兩輛車可以用來運煤。如果每次運煤的車都裝滿，怎樣安排能恰好運完8噸煤？(題目已知藍卡車載質量2噸，紅卡車載質量是3噸)。教師引導學生利用列表法得出最后的結果：

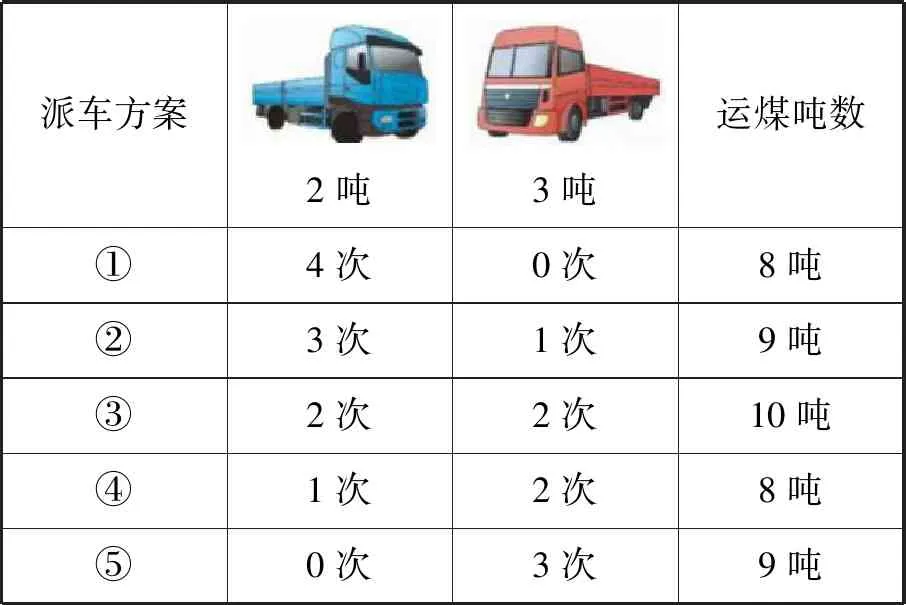
派車方案2噸3噸運煤噸數①4次0次8噸②3次1次9噸③2次2次10噸④1次2次8噸⑤0次3次9噸

為了驗證結果的正誤，一般會采用如下檢驗的方法：

方法一：4×2=8(噸)，2×1+3×2=8(噸)，證明方案①和方案④正確。然而，這并不是唯一的方法，教師還可以引導學生從其他角度入手檢驗，如：

方法二：畫圖檢驗。用1個圓圈代表1噸煤，畫出10個圓圈即10噸煤，根據方案①，每2噸圈一圈，圈4次剛好圈完，方案①得證。再根據方案④，每2噸圈1圈，圈1次，再每3噸圈一圈，圈2次，也正好圈完，方案④得證。

方法三：“除法”檢驗。假設全部用藍卡車運輸，8÷2=4(次)，需要運4次，驗證了方案①；假設用紅卡車運輸，8÷3=2(次)……2(噸)，說明紅卡車需要運2次，還剩2噸，正好用藍卡車運輸1次，驗證了方案④。

通過對比，我們發現：與方法一不同的是，方法二用畫一畫的方法進行驗證，數形結合進行回顧與反思；方法三則逆向思考，用載貨的結果與卡車運載量的關系入手進行倒推。由此可見，老師給予學生反思的空間就能看到具有個性化的方法，打開學生思維的大門，久而久之，學生對這一環節的興趣逐步提升，不斷迸發出創新的想法。只有教師意識到回顧與反思環節在培養學生思維中的重要地位，才能尊重多樣的檢驗方法，給學生的“驗”留出思考的時間和空間，鼓勵學生大膽思考，自信表達，真正給學生的思維活動續航。

3.建構模型，歸納總結，發展高階思維

回顧與反思是解決問題中必不可少的環節，但由于課堂時間有限，不少時候教師會把它挪到練習以后，甚至忽略這個過程。聽課時，我們經常看到這樣模式化處理方式：這節課你學會了什么？學生往往照著板書再念一遍，板書念完了，課也就結束了。這樣就導致當課程結束的時候，學生對知識的理解停留在碎片化的認識上，不深刻不透徹，難以形成完整的知識體系和數學模型。如果教師能在這個環節引導學生通過小組合作的形式利用思維導圖等有效的方式歸納總結，就能幫助學生抽象出例題背后的數學模型，當數學模型在學生腦海里建構完成后，再利用這個模型舉一反三，在這過程中逐步培養學生問題解決、團隊協作、獲取隱性知識的能力，從而有效地發展學生的高階思維。

以三年級上冊第五單元《倍的認識》例題3《求一個數的幾倍是多少》為例：“軍棋的價錢是8元，象棋的價錢是軍棋的4倍，象棋的價錢是多少元？”教學中教師引導學生利用畫圖的方法理解求象棋的價錢，就是求4個8是多少，得出算式：8×4=32(元)。回顧與反思的環節，教材給出一個提示：“32元是8元的4倍嗎？”很明顯教材側重于檢驗結果的正誤。教師們會引導學生采用上一節課求倍數的知識，利用除法反證乘法，求出32正好是8的4倍。但是，如果把例題3《求一個數的幾倍是多少》和例題2《求一個數是另一個數的幾倍》用畫圖的方式放在一起，對比發現，兩者其實就是乘法和除法的數學模型。

先看例題2：求擦座椅的人數是掃地的幾倍，就相當于求12里面有幾個4，即除法模型的其中一種：把一個數每幾個分成一份，可以分成幾份。因此求A是B的幾倍，本質上就是求把A每B個分成一份，可以分成幾份，可以用A÷B來計算。

再看例題3：已知軍棋價錢是8元，象棋價錢是軍棋的4倍，求象棋的價錢，就是求4個8元是多少？這即是乘法的數學模型：求幾個幾相加是多少。因此，如果進一步引伸，求A的B倍是多少，就是求B個A相加是多少，可以用A×B來計算。

如果在回顧與反思的環節中先將這兩個例題進行對比，進而追問引發學生思考：“比較例2和例3，為什么例2要用除法，例3要用乘法？”通過小組討論、生生對話的形式，圍繞核心的問題進行辨析，從而提煉出兩者本質上的數學模型，學生很容易就能理解這部分內容既是新知又是舊知，將新舊知識打通，形成新的知識結構，學生對數學模型理解得越深刻，就越不容易出現在倍數問題中常見的乘除法混淆的現象，這比單純的檢驗結果更有意義。

綜上所述，回顧與反思不僅不會拖累深度學習的進度，還是促進深度學習的重要利器，它不僅緊扣了深度學習的思想，也為單元的整體知識建構提供了平臺。同理，數學模型的建構不僅是新課探究環節所追崇的，回顧與反思同樣能夠實現這一教學理想。若在這一環節能引導學生跳出例題看本質，從例題中抽象出數學模型，實現知識點的自然遷移，知識體系的充盈就不在話下。轉變思想，“回顧與反思”就是提升課堂效率和質量的倍增器，在回顧中鞏固，在反思中提升。長期的堅持更會使學生練就一副火眼金睛，“看山不是山，看水不是水”，看待新知都似曾相識，難點自然迎刃而解。回顧與反思，應該成為課堂上又一熠熠生輝的亮點，它為我們構筑一個生機盎然的深度學習的課堂生態。