殊途同歸：認知診斷與知識追蹤*——兩種主流學習者知識狀態建模方法的比較

戴 靜 顧小清 江 波

殊途同歸：認知診斷與知識追蹤*——兩種主流學習者知識狀態建模方法的比較

戴 靜 顧小清[通訊作者]江 波

（華東師范大學 教育信息技術學系，上海 200062）

學習者知識狀態建模是建立個性化學習系統的重要任務之一。目前，學習者知識狀態建模的主流方法有兩種，分別是心理測量領域專家提出的認知診斷方法和人機交互領域專家提出的知識追蹤方法。為了更恰當地將這兩種方法應用于智能教育領域，文章圍繞以何建模、如何建模、結果為何、如何應用這四個學習者建模的關鍵問題，從輸入維度的可擴展性、模型參數的可適應性、輸出結果的精益求精、助力個性化推薦服務四個方面，對認知診斷方法和知識追蹤方法進行論述比較。總的來說，認知診斷方法適用于靜態評估且在輸出結果方面更為精細化、多樣化，而知識追蹤方法適用于動態預測且在輸入維度方面更具可擴展性。通過研究，文章期望為研究者合理應用這兩種方法以服務于個性化學習系統提供參考。

學習者建模；知識狀態；認知診斷；知識追蹤

近年來，《教育信息化2.0行動》、《中國教育現代化2035》等系列政策均強調利用智能技術輔助實現個性化學習。個性化學習的本質在于，根據學習過程數據對學習者進行全面刻畫，據此適時進行學習路徑與學習資源推薦等個性化干預[1]。學習者模型作為個性化干預的依據，是個性化學習系統的重要組成模塊，可將其看作一組學習者特征的集合，包括知識狀態、情感狀態、能力狀態等[2]。但是，針對學習者情感、能力的建模研究目前還處于探索階段，個性化學習系統仍以學習者知識狀態作為主要的推薦依據[3]。也正因此，如何對學習者知識狀態進行建模一直是個性化學習領域關注的重點內容。為此，本研究選取認知診斷與知識追蹤這兩種學習者知識狀態建模的主流方法進行比較，以期為研究者合理應用個性化學習系統提供參考。

一 學習者知識狀態建模概述

學習者知識狀態建模指通過學習者個體的作答行為與結果數據對個性化的知識狀態進行刻畫的過程[4]。截至2021年7月24日，在中國知網數據庫以“學習者建模”或“學習者模型”為關鍵詞、以“CSSCI”為來源類別，檢索到86篇文獻；在Web of Science-SSCI引文索引數據庫以“Learner model”或“Student model”為關鍵詞，檢索到141篇文獻。文獻分析表明，學習者建模研究關注四個關鍵問題：①“以何建模”，即采用何種數據作為建模輸入；②“如何建模”，即關注模型本身，如模型參數類別與數量等；③“結果為何”，即模型的輸出是什么、如何改善當前方法所得結果的局限性等；④“如何應用”，即如何用學習者建模結果服務個性化學習。

就學習者知識狀態的建模方法而言，目前有覆蓋模型、微分模型、攝動模型、認知診斷、偏差模型、知識追蹤等[5]。其中，覆蓋模型是通過比較學習者知識與專家知識來發現學習者缺乏的知識技能，而微分模型和攝動模型是基于覆蓋模型的改進；認知診斷是對具體的認知加工過程或子技能進行評估；偏差模型是通過學習者的問題解決路徑與專家解決路徑的偏差，來發現學習者特定知識點的不足；知識追蹤是通過學習者與習題的交互數據，預測學習者的知識狀態。

認知診斷和知識追蹤是被廣泛采納的兩種學習者知識狀態建模方法[6]，但認知診斷來源于心理測量領域，而知識追蹤來源于人機交互領域。這兩種由跨學科專家提出的看似不相關的方法，在個性化學習系統興起后相互碰撞，為建立學習者模型提供了有力手段。然而，在個性化學習的實踐中，選用哪種方法一般取決于研究者自身特長，鮮有研究對這兩種方法進行比較。因此，本研究圍繞以何建模、如何建模、結果為何、如何應用這四個學習者建模的關鍵問題，比較認知診斷和知識追蹤這兩大學習者建模方法，研究思路如圖1所示。

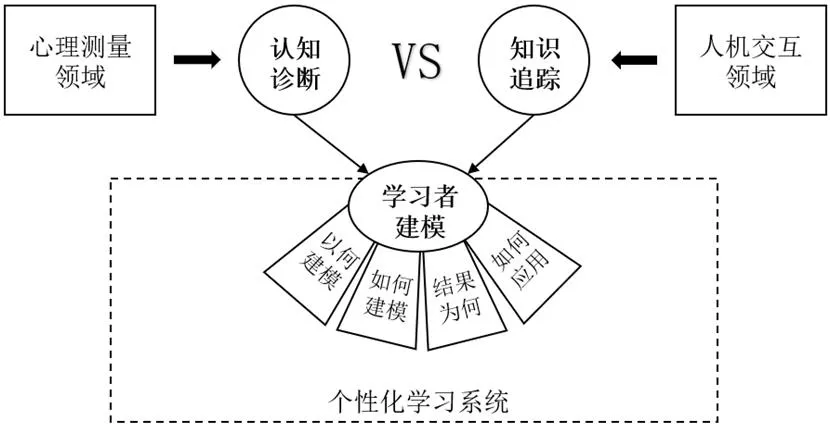
圖1 研究思路

二 認知診斷：心理測量領域的建模方法

1 起源

認知診斷（Cognitive Diagnosis，CD）是心理測量領域對認知加工過程或知識技能進行診斷評估的產物[7]。20世紀80年代，隨著心理測量學的發展，人們不滿足于從宏觀上測量和評價學生能力，因而開始探索學習者內部心理的加工過程。于是，繼經典測量理論（Classical Test Theory，CTT）、概化理論（Generalizability Theory，GT）和項目反應理論（Item Response Theory，IRT）之后，認知診斷成為新一代測驗理論的核心。

2 發展歷程

認知診斷的發展歷程中有兩個里程碑式的模型：一個是1973年Fischer[8]提出的線性邏輯斯蒂特質模型（Linear Logistic Trait Model，LLTM），該模型考慮了正確回答問題所需的認知成分，以各個認知屬性的難度代替Rasch模型（單參數邏輯斯蒂模型）中的題目難度參數，由IRT向CD跨越了一大步，但此時LLTM還不能進行認知屬性的評估；另一個是1983年Tatsuoka[9]提出的規則空間模型（Rule Space Model，RSM），該模型首創性地使用Q矩陣來代替LLTM中的認知屬性難度成分，此后Q矩陣的建立便成為了認知診斷的關鍵步驟。基于Q矩陣，產生了一系列認知診斷模型，如針對選擇題、填空題、判斷題等的二級評分認知診斷模型和針對計算題、應用題、作文題等的多級評分認知診斷模型。

3 典型模型

（1）二級評分認知診斷模型

二級評分認知診斷的典型模型包括DINA[10]、DINO[11]、NIDA[12]、NIDO[13]、C-RUM[14]、R-RUM[15]、M2PL[16]等，具體如表1所示。在公式中，q=1，表示題目考察了屬性；q=0，表示未考察。a=1，表示學生掌握屬性；a=0，表示未掌握。X=1，表示學生對于題目作答正確；X=0，表示作答錯誤。除通用參數外，每個模型均包含特有參數，如DINA模型包含兩個定義在題目水平上的參數，即失誤參數s和猜測參數g：若學生掌握了題目考察的所有屬性，則作答正確的概率為1-s；反之，則作答正確的概率為g。

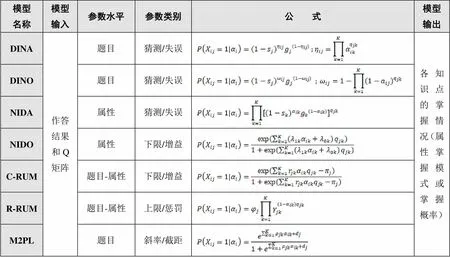
表1 二級評分認知診斷的典型模型

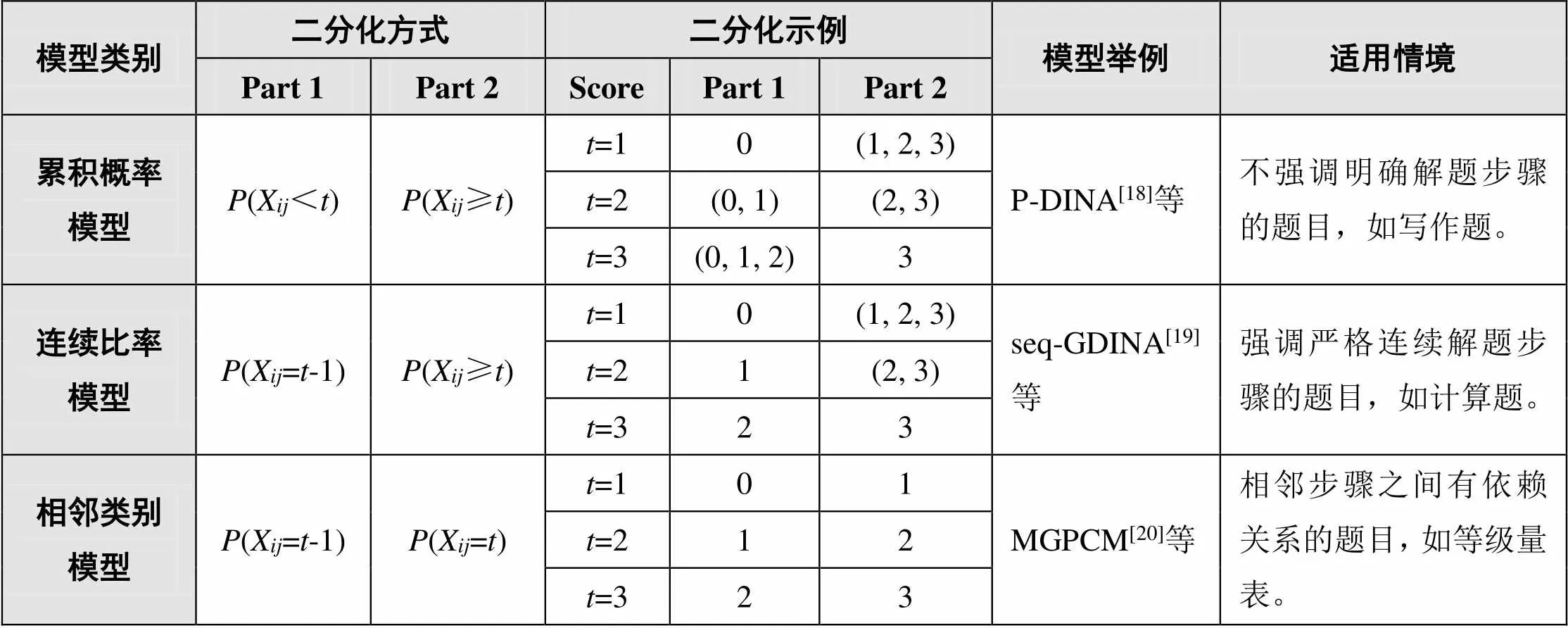
表2 多級評分認知診斷的典型模型

（2）多級評分認知診斷模型

針對多級評分題目的認知診斷模型，本質是對每一個得分等級進行建模，從而將多級評分問題轉化為二級評分問題。按照具體二分化轉換方法的不同，多級評分認知診斷模型可分為累積概率模型（Cumulative Probability Model）、連續比率模型（Continuation-Ratio Model）和相鄰類別模型（Adjacent-Category Model）[17]，如表2所示。其中，表示得分等級（Score），若題目的滿分為3分，則的取值為{0, 1, 2, 3}。四種得分等級可簡單理解為未答對（0）、答對一個步驟（1）、答對兩個步驟（2）、全部答對（3）。例如，累積概率模型針對每個得分等級或步驟，將其二分化為(X＜)和(X≥)；被試在第題恰得分的概率為得分及以上的概率減去得+1分及以上的概率，即(X=t|a)(X≥t|a)-(X≥+1|a)。

三 知識追蹤：人機交互領域的建模方法

1 起源

知識追蹤（Knowledge Tracing，KT）是計算機科學與心理學結合的產物，由卡內基梅隆大學計算機科學學院人機交互研究所專家Corbett等[21]于1995年引入智能教育領域，后成為個性化學習系統中學習者知識狀態建模的主流方法。知識追蹤的初衷是對知識習得過程中的知識狀態動態建模，確定學習者何時掌握了一項特定技能。知識追蹤根據學習者的歷史作答行為數據，包括作答題目、題目對應的知識點、作答結果序列，預測下次給定題目的作答結果與知識狀態。

2 發展歷程

早期的知識追蹤研究以貝葉斯知識追蹤模型為主，后因深度學習技術的發展，深度知識追蹤模型也成為研究熱點[22]。自1995年以來，貝葉斯知識追蹤的研究主要圍繞改善其本身的局限性展開，如貝葉斯知識追蹤假設知識狀態只分為掌握和未掌握兩種、學習者不會遺忘知識點、只針對單個知識點建模等。直至2015年，第一個深度知識追蹤模型才出現，即Piech等[23]提出使用循環神經網絡（Recurrent Neural Network，RNN）及其變體長短期記憶（Long Short-Term Memory，LSTM）神經網絡，來預測學習者的作答結果和知識狀態。之后，研究者主要通過增加輸入特征[24]、改進神經網絡等[25]，嘗試進一步提升預測效果。

3 典型模型

（1）貝葉斯知識追蹤模型

貝葉斯知識追蹤（Bayesian Knowledge Tracing，BKT）模型本質上可以看作是隱馬爾可夫模型（Hidden Markov Model，HMM），如圖2所示。其中，(a)部分為HMM的一般形式，包括隱狀態（S）、觀測狀態（y）、初始概率分布、轉移概率矩陣和發射概率五個元素。(c)部分為BKT實例，結合(a)部分來看，可知BKT針對單個知識點建模，隱狀態為知識點掌握情況，包括掌握（M）或未掌握（N）；觀測狀態為作答結果，包括正確（1）或錯誤（0）。(b)部分則顯示了BKT中影響狀態轉換的參數，具體有四個：(0)，即開始學習之前掌握該知識點的概率；()，即通過學習之后該知識點從未被掌握到被掌握的概率，結合BKT不存在遺忘現象的假設可得轉移概率矩陣；()，即未掌握該知識點卻答對題目的概率；()，即掌握了該知識點卻答錯的概率。

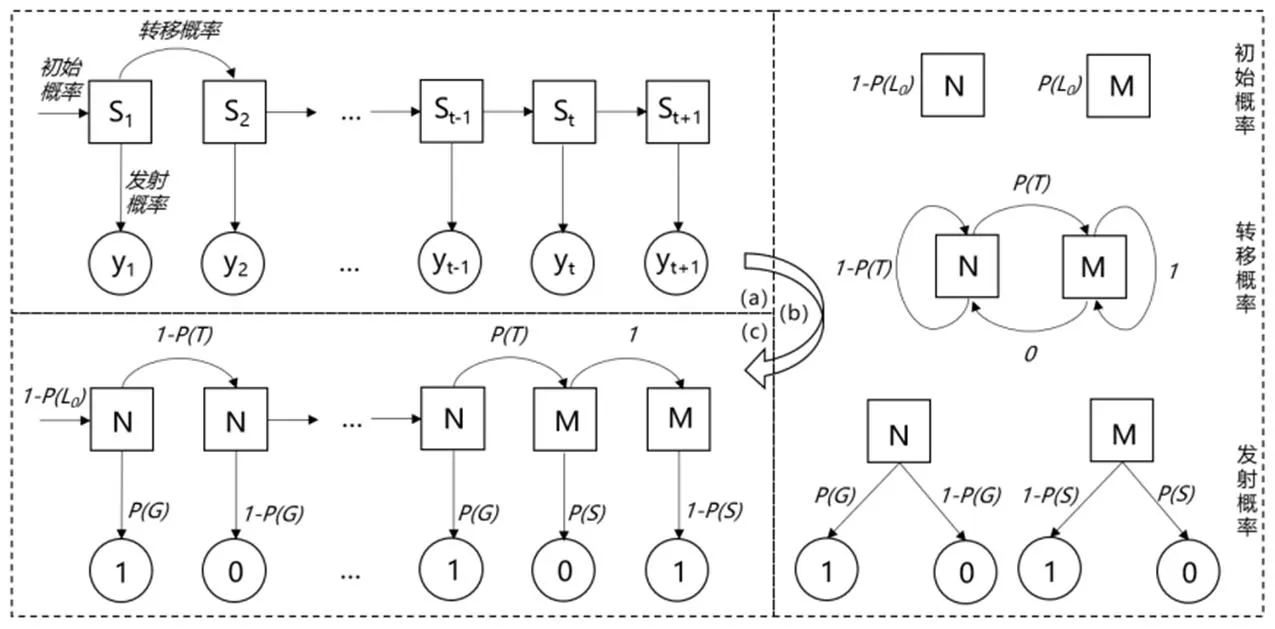
圖2 貝葉斯知識追蹤模型

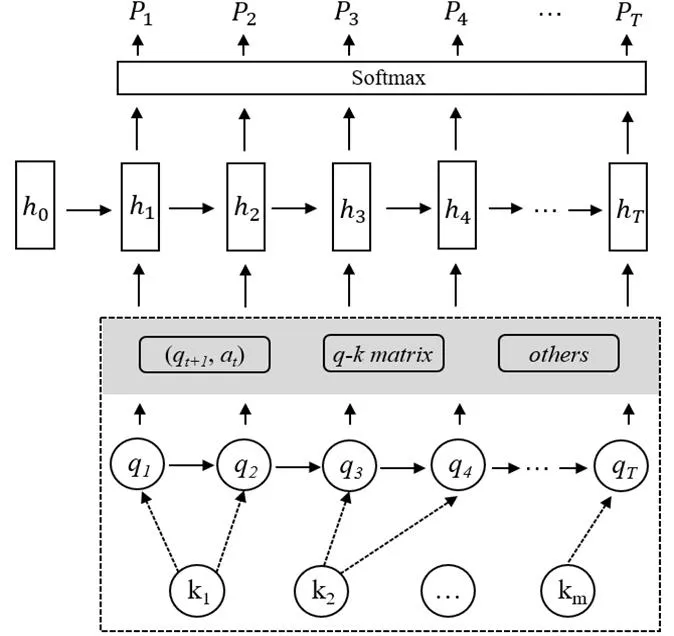
圖3 深度知識追蹤模型

（2）深度知識追蹤模型

深度知識追蹤（Deep Knowledge Tracing，DKT）模型將深度學習技術應用于知識追蹤任務，如圖3所示。學習者在學習過程中進行了多次題目練習(1,2, …,T)，每一道題目都標注了知識點(1,2, …,m)，將學生在第次之前的作答結果(t={t,t})序列、下一道題編號(t+1)、所有題目與知識點的對應關系矩陣以及其他相關信息作為輸入，經過神經網絡的隱藏層，在輸出層預測第+1次作答時的知識點掌握概率向量t+1。

四 認知診斷與知識追蹤的比較

針對學習者建模的四個關鍵問題“以何建模”“如何建模”“結果為何”“如何應用”，結合對表1、表2、圖2和圖3的分析，本研究從輸入數據、模型參數、輸出結果、應用初衷四個維度，對認知診斷和知識追蹤的典型模型進行初步比較，結果如表3所示。其中，多級評分認知診斷可以轉化為二級評分認知診斷問題，故兩者未分開論述；而貝葉斯知識追蹤模型與深度知識追蹤模型的差異較大，故在下文中將兩者分開論述。

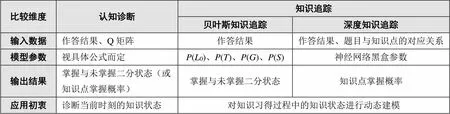
表3 認知診斷與知識追蹤典型模型的初步比較

由表3可知，認知診斷與深度知識追蹤的輸入數據相近，區別在于Q矩陣不僅包括題目與知識點的對應關系，還隱含了知識點之間的層級關系；而貝葉斯知識追蹤并非不考慮題目與知識點的對應關系，只是其針對單個知識點建模，所有題目只對應當前這一個知識點，故不會特意列出。從模型參數維度來看，認知診斷的參數根據不同的統計公式而定，表1中已有說明；貝葉斯知識追蹤采用HMM統計模型，最典型的貝葉斯知識追蹤包括初始掌握概率(0)、學習概率()、猜測概率()、失誤概率()四個參數；深度知識追蹤則采用不同于統計模型的神經網絡結構，其內部參數在教學方面不具有可解釋性。從輸出結果維度來看，認知診斷和貝葉斯知識追蹤通常以掌握或未掌握二分狀態來呈現，但前者也可以計算知識點的掌握概率；深度知識追蹤通常以知識點掌握概率呈現。從應用初衷維度來看，認知診斷是為了診斷學習者當前時刻的知識狀態，而知識追蹤是為了通過動態監測來發現學習者何時掌握了某一知識點，但兩者本質上都是評估學習者的知識狀態。總體而言，認知診斷與知識追蹤的輸入數據和輸出結果相近、模型參數有明顯差異，在學習者知識狀態建模方面有殊途同歸之效。

然而，大規模個性化學習趨勢的發展對學習者建模提出了進一步的要求。就“以何建模”而言，需在輸入數據中嘗試增加各項影響學習者知識狀態的因素；就“如何建模”而言，需探索能夠體現知識狀態個性化特征的模型參數；就“結果為何”而言，需不斷思考如何改善當前方法所得結果的局限性；就“如何應用”而言，需明確各建模方法的應用場景與應用方法。為滿足這四個方面的需求，認知診斷與知識追蹤都進行了持續的擴展研究。

1 以何建模：輸入維度的可擴展性

學習者建模的輸入維度正在從單一化向多維化轉變，可擴展性成為學習者建模的需求之一。以往，評估學習者的知識狀態多從作答結果（對錯、得幾分）單一維度來看；后來，隨著大數據技術及各種數據采集設備的完善，學習者信息維度（如作答行為、情緒、個性特征）、知識點信息維度（如知識點之間的層級關系）等影響評估結果的因素也被納入建模維度。

①學習者信息維度。貝葉斯知識追蹤模型一般通過增設節點變量或外生變量的形式，來擴展學習者信息維度；節點變量扮演外顯證據的角色，如Spaulding等[26]嘗試通過增加情緒觀測節點（微笑、困惑等）來提高預測性能；外生變量扮演影響因素的角色，如González-Brenes等[27]提出了一個類似非齊次隱馬爾可夫模型的知識追蹤框架，該框架可納入影響狀態轉移概率、發射概率的各種特征。深度知識追蹤模型的本質形式是深度神經網絡，本就可以接受多維輸入，如Zhang等[28]增加學習者第一次作答嘗試的時間、嘗試的次數等行為數據，作為深度知識追蹤的輸入維度。相比而言，在認知診斷模型中增加學習者信息維度的研究目前并不多見。

②知識點信息維度。認知診斷模型的Q矩陣中已隱含了知識點之間的層級關系，即大多數認知診斷模型已默認將知識點之間的關系維度作為輸入。貝葉斯知識追蹤模型只針對單個知識點進行建模，一般不考慮知識點關系維度；但也有少數研究者對此進行了嘗試，如Huang等[29]提出了融入知識層級關系的貝葉斯網絡建模框架。深度知識追蹤模型可對多個知識點進行建模，知識點之間的關系作為一個研究點備受關注，如Chen等[30]嘗試以順序配對的形式將知識點之間的先決關系作為模型的輸入。值得一提的是，深度知識追蹤模型中每道題或每道題的某一個步驟通常只與一個知識點掛鉤，將多個知識點一起考察，本質上是不同知識點順序上的交叉練習，而非真正的混合練習。

總體來說，認知診斷模型均為概率公式的形式，無法靈活地增加學習者行為、情緒等維度。貝葉斯知識追蹤模型只針對作答結果單一維度建模，但可利用貝葉斯網絡本身的可塑性來增加其他維度。深度知識追蹤模型以人工神經網絡為載體，擴展輸入維度正是其優勢的體現。因此，在輸入維度方面，知識追蹤模型比認知診斷模型更具可擴展性。

2 如何建模：模型參數的可適應性

認知診斷與知識追蹤的建模過程相同，大體可分為數據采集和參數估計（或模型訓練）。模型的參數是體現模型差異的重要方面，通過各類參數以準確表征每一個學習者的知識狀態是建模的關鍵任務。刻畫知識狀態的參數大致可分為三個層面：題目層面、屬性層面和學習者層面，這三個層面分別針對每一道題、每一個屬性或每一個學習者設置適應性參數。以“猜答案”這一現象為例，若將參數置于題目層面，可解釋為不同題目被猜對的概率是不同的；若將參數置于屬性層面，可解釋為不同知識點未被掌握卻被成功應用的概率是不同的；若將參數置于學習者層面，則可解釋為不同學習者猜對題目的概率是不同的。無論是典型模型的常規參數，還是后期擴展研究的新增參數，都體現了這三個層面的適應性。

①常規參數。在認知診斷模型中，既有針對題目層面的參數建模，如DINA、DINO模型中的猜測和失誤參數；也有針對屬性層面的參數建模，如NIDO模型中的下限和增益參數；還有針對屬性和題目交叉層面的參數建模，如R-RUM模型中的懲罰參數。貝葉斯知識追蹤模型是針對屬性層面的參數建模，即當所有學習者就同一知識點對所有題目進行作答時，其所擁有的初始掌握概率、學習概率、猜測概率、失誤概率這四個參數是一樣的。后來，有研究者在題目層面進行了適應性嘗試，如Pardos等[31]提出KT-IDEM模型，賦予每道題一個猜測概率和一個失誤概率，那么道題就有2×+2個參數。也有研究者在學習者層面進行了適應性嘗試，如Pardos等[32]提出對于同一知識點，每個學習者應擁有個性化的初始掌握概率和學習概率；Lee等[33]的研究表明，擁有適應性參數的模型比典型模型更具有教學指導意義。而在深度知識追蹤模型中，由于深度學習技術的“黑盒”特質，神經網絡層之間的權重等參數暫不具有可解釋的教學意義。

②新增參數。遺忘特性是后期研究嘗試最多的新增參數。貝葉斯知識追蹤模型假設學習者不存在遺忘現象，但Qiu等[34]發現該模型對于學習者的預測表現（一天或更長時間之后）優于實際情況，于是提出可按照是否為學習當天分別采用不同屬性層面的遺忘參數——當天的遺忘參數(s)和第二天及以后的遺忘參數(n)；而Nedungadi等[35]依據上次嘗試作答和當前嘗試作答的具體時間間隔，提出以時間衰減函數的形式引入遺忘參數。深度知識追蹤模型雖然無法直接增加具有顯著教育意義的遺忘參數，但可在輸入參數中增加同一知識點最近兩次作答之間的時間間隔、無知識點限制情況下最近兩次作答之間的時間間隔等體現遺忘特性的信息[36]。認知診斷模型本意是針對測驗情境而未考慮遺忘特性的典型模型。

總體來說，在認知診斷模型中，針對題目層面、屬性層面、屬性與題目交叉層面的參數建模均已進行了嘗試，并已開發出相應的模型。貝葉斯知識追蹤模型的參數都屬于屬性層面，但可通過題目層面和學習者層面進一步細化，以賦予每一道題或每一個學習者個性化的特征。深度知識追蹤模型的參數不可解釋，暫不具有顯著的教學意義。值得一提的是，選擇不同層面的參數，僅意味著采用不同的建模思路，并無優劣之分。

3 結果為何：輸出結果的精益求精

學習者建模的目的就是獲得準確、精細的知識狀態。就輸出結果的精細化程度而言，有些模型僅可展示是否掌握的離散值，有些模型卻可展示具體掌握程度的連續值。就輸出結果的準確度而言，除增加輸入數據、豐富模型參數外，建模時還應在一定程度上考慮各種因素，如一道題考察多個知識點，掌握一道題中涉及幾個知識點才可能答對該題、該知識點是否被標全等。

①輸出結果的精細化程度。認知診斷模型通常以是否掌握二元狀態來描述，但實質上二元狀態是在計算概率值后劃分而來的；也有少數多維IRT模型以能力值（通常取值范圍為[-4, +4]）來表征每一個知識維度的掌握情況。貝葉斯知識追蹤模型的輸出結果依賴于HMM框架中的隱狀態，通常為掌握、未掌握兩種；也有研究者嘗試進行更為精細化的劃分，如Zhang等[37]提出在二分知識掌握情況中間加入過渡狀態，將建模結果分為三種：掌握、可能掌握、未掌握。深度知識追蹤模型可獲得學習者對每一個知識點的掌握概率，其范圍為0～1之間的連續值。

②輸出結果的準確度。對于一道題考察多個知識點的現象，現實生活中并不少見。認知診斷模型相關研究對此思考較多，并衍生出各種模型。例如，掌握一道題中涉及的幾個知識點才可能答對該題，針對這一問題，不同的認知診斷模型采用了不同的假設：DINA模型假設所有知識點全部掌握才能答對；DINO模型假設只要掌握其中一個知識點就可能答對；R-RUM模型則假設隨著掌握的知識點數量增加，答對的概率隨之增加。又如，針對一道題考察了多個知識點但知識點并未標注完全的情況，RUM模型作為R-RUM簡化前的版本，增加了一個參數表示Q矩陣以外被忽略的殘余能力。貝葉斯知識追蹤模型并沒有考慮到這一問題，但也有Xu等[38]嘗試采用動態貝葉斯網絡追蹤每一個知識點。深度知識追蹤模型的相關研究也不多，Xiong等[39]表示DKT在處理該問題時將單條作答記錄擴展成多條記錄，這是DKT的效果顯著優于BKT的原因；但是，DKT的輸出結果存在波動性，即調換答題順序后所得的知識狀態結果不同。

總體來說，認知診斷模型的建模結果既可以是連續值，也可以是離散值，且對一道題考察多個知識點等細節問題做出了良好的應對。貝葉斯知識追蹤模型的建模結果只有掌握或未掌握兩種值，雖然也有研究嘗試突破二元狀態，但由于HMM模型本身隱狀態的限制，使其只能在離散狀態的個數上進行突破，并不能將離散過渡改為連續過渡。深度知識追蹤模型可通過權重參數計算0～1之間的連續值，準確度也優于貝葉斯知識追蹤，但存在結果波動性的問題。

4 如何應用：助力個性化推薦服務

學習者建模的價值不止于獲得學習者知識狀態，更重要的是應用建模結果進行個性化推薦。首先，需明確認知診斷和知識追蹤兩種方法在個性化學習系統中的應用場景，這是保證建模結果的第一步。然后，根據建模結果，應用可行的方法為學習者提供個性化學習資源推薦等服務。

①應用場景。認知診斷適用于短時間內可完成的測試或作業場景，而知識追蹤更適用于持續性的日常練習場景。具體來說，用于認知診斷模型的作答數據，一般是在學習者知識狀態未發生改變的時間范圍內；而知識追蹤是為了在學習者進行知識習得的過程中，對動態變化的知識狀態進行建模。從模型本身也可看出，用于貝葉斯知識追蹤的貝葉斯網絡和用于深度知識追蹤的循環神經網絡本就是針對時序問題的模型；對于相同的題目和相同的答案，若做題順序不同，知識追蹤模型得到的知識狀態結果也會不同。

②應用方法。根據認知診斷和知識追蹤方法獲得認知優勢與劣勢后，一方面可直接推薦與未掌握知識點相對應的資源，以進行針對性補救；另一方面可與協同過濾、矩陣分解等推薦領域常用的方法結合提供學習者知識狀態信息，以提高推薦的有效性。除此通用方法之外，認知診斷特有一種已成體系的推薦方法——認知診斷自適應測試（Cognitive Diagnostic Computerized Adaptive Testing，CD-CAT）中的選題算法，其本意是高效測量學習者的知識狀態及能力水平，本質上也是針對每一個學習者予以個性化題目推薦。

總體來說，認知診斷和知識追蹤方法的出發點不同，前者為靜態診斷，尤其適用于測試場景；后者為動態預測，更適用于能夠體現知識狀態變化的知識習得過程。認知診斷和知識追蹤均可與協同過濾、矩陣分解等常用方法相結合，以實現學習資源的有效、個性化推薦。但相較于知識追蹤而言，認知診斷還可借鑒自適應測試中的選題策略向每個學習者推薦個性化題目。

五 結論與建議

本研究圍繞學習者建模需要考慮的四個關鍵問題，即以何建模、如何建模、結果為何、如何應用，論述分析認知診斷和知識追蹤這兩種方法的特點及優劣勢。總結來說，在輸入維度方面，知識追蹤比認知診斷更具可擴展性；在模型參數方面，兩者采用的建模思路不同，因而參數類別不同；在輸出結果方面，認知診斷比知識追蹤更為精細化、多樣化；在建模應用方面，認知診斷適用于靜態評估，而知識追蹤適用于動態預測。

為了合理采用這兩種方法以服務于智能教育領域，本研究提出以下建議：①針對兩種方法的優劣勢進行算法的整合與改進研究。例如，Wang等[40]提出神經認知診斷框架，既保留了認知診斷方法的準確性和可解釋性，又納入了神經網絡結構較強的函數擬合能力，可以說綜合了認知診斷和深度知識追蹤兩種方法的優勢。②根據場景和數據源來選擇學習者建模方法。若是根據個性化學習系統中的自適應測試或普通測試場景做題數據來刻畫學習者知識狀態，建議選擇認知診斷方法；若是根據有智能提示的導學場景做題數據來刻畫學習者知識狀態，則建議選擇知識追蹤方法——若是擬納入學習風格、答題時長、作答嘗試次數等數據來刻畫學習者知識狀態，尤其建議選擇深度知識追蹤模型。

[1]Pardo A, Jovanovic J, Dawson S, et al. Using learning analytics to scale the provision of personalised feedback[J]. British Journal of Educational Technology, 2019,(1):128-138.

[2]Normadhi N B A, Shuib L, Nasir H N M, et al. Identification of personal traits in adaptive learning environment: Systematic literature review[J]. Computers & Education, 2019,(3):168-190.

[3]萬海鵬,余勝泉,王琦,等.基于學習認知地圖的開放學習者模型研究[J].現代教育技術,2021,(4):97-104.

[4]黃濤,王一巖,張浩,等.智能教育場域中的學習者建模研究趨向[J].遠程教育雜志,2020,(1):50-60.

[5]張舸,周東岱,葛情情.自適應學習系統中學習者特征模型及建模方法述評[J].現代教育技術,2012,(5):77-82.

[6]Abyaa A, Khalidi I M, Bennani S. Learner modelling: Systematic review of the literature from the last 5 years[J]. Educational Technology Research and Development, 2019,(5):1105-1143.

[7]Henson R, Douglas J. Test construction for cognitive diagnosis[J]. Applied Psychological Measurement, 2005,(4):262-277.

[8]Fischer G H. The linear logistic test model as an instrument in educational research[J]. Acta Psychologica, 1973,(6):359-374.

[9]Tatsuoka K K. Rule space: An approach for dealing with misconceptions based on item response theory[J]. Journal of Educational Measurement, 1983,(4):345-354.

[10][12]Junker B W, Sijtsma K. Cognitive assessment models with few assumptions, and connections with nonparametric item response theory[J]. Applied Psychological Measurement, 2001,(3):258-272.

[11]Templin J L, Henson R A. Measurement of psychological disorders using cognitive diagnosis models[J]. Psychological Methods, 2006,(3):287-305.

[13]Rupp A A, Templin J, Henson R A. Diagnostic measurement: Theory, methods, and applications[M]. New York: Guilford Press, 2010:131-135.

[14]Maris E. Estimating multiple classification latent class models[J]. Psychometrika, 1999,(2):187-212.

[15]Hartz S, Roussos L. The fusion model for skills diagnosis: Blending theory with practicality[R]. Princeton, NJ: Educational Testing Service, 2008:5-10.

[16]Reckase M D. Multidimensional item response theory[M]. New York, NY: Springer, 2009:86.

[17]高旭亮,龔毅,王芳.多級評分認知診斷模型述評[J].心理科學,2021,(2):457-464.

[18]涂冬波,蔡艷,戴海琦,等.一種多級評分的認知診斷模型:P-DINA模型的開發[J].心理學報,2010,(10):1011-1020.

[19]Ma W, Torre J de la. A sequential cognitive diagnosis model for polytomous responses[J]. British Journal of Mathematical and Statistical Psychology, 2016,(3):253-275.

[20]Yao L, Schwarz R D. A multidimensional partial credit model with associated item and test statistics: An application to mixed-format tests[J]. Applied Psychological Measurement, 2006,(6):469-492.

[21]Corbett A T, Anderson J R. Knowledge tracing: Modeling the acquisition of procedural knowledge[J]. User Modeling and User-adapted Interaction, 1995,(4):253-278.

[22]張暖,江波.學習者知識追蹤研究進展綜述[J].計算機科學,2021,(4):213-222.

[23]Piech C, Spencer J, Huang J, et al. Deep knowledge tracing[A]. Proceedings of the 28th International Conference on Neural Information Processing Systems[C]. Massachusetts: MIT Press, 2015:505-513.

[24][28]Zhang L, Xiong X, Zhao S, et al. Incorporating rich features into deep knowledge tracing[A]. Proceedings of the 4th ACM Conference on learning@scale[C]. New York: Association for Computing Machinery, 2017:169-172.

[25]Zhang J, Shi X, King I, et al. Dynamic key-value memory networks for knowledge tracing[A]. Proceedings of the 26th International Conference on World Wide Web[C]. New York: Association for Computing Machinery, 2017:765-774.

[26]Spaulding S, Breazeal C. Affect and inference in Bayesian knowledge tracing with a robot tutor[A]. Proceedings of the10th Annual ACM/IEEE International Conference on Human-Robot Interaction Extended Abstracts[C]. New York: Association for Computing Machinery, 2015:219-220.

[27]González-Brenes J, Huang Y, Brusilovsky P. General features in knowledge tracing to model multiple subskills, temporal item response theory, and expert knowledge[A]. Proceedings of the 7th International Conference on Educational Data Mining[C]. Massachusetts: International Educational Data Mining Society, 2014:84-91.

[29]Huang Y, Hollstein J D G, Brusilovsky P. Modeling skill combination patterns for deeper knowledge tracing[A]. Proceedings of the 24th International Conference on User Modeling, Adaptation, and Personalization (Extended Proceedings)[C]. Berlin: Springer, 2016:1-9.

[30]Chen P, Lu Y, Zheng V W, et al. Prerequisite-driven deep knowledge tracing[A]. Proceedings of 2018 IEEE International Conference on Data Mining (ICDM)[C]. Piscataway: The Institute of Electrical and Electronics Engineers, 2018:39-48.

[31]Pardos Z A, Heffernan N T. KT-IDEM: Introducing item difficulty to the knowledge tracing model[A]. Proceedings of the 19th International Conference on User Modeling, Adaptation, and Personalization[C]. Berlin: Springer, 2011:243-254.

[32]Pardos Z A, Heffernan N T. Modeling individualization in a Bayesian networks implementation of knowledge tracing[A]. Proceedings of the 18th International Conference on User Modeling, Adaptation, and Personalization[C]. Berlin: Springer, 2010:255-266.

[33]Lee J I, Brunskill E. The impact on individualizing student models on necessary practice opportunities[A]. Proceedings of the 5th International Conference on Educational Data Mining[C]. Massachusetts: International Educational Data Mining Society, 2012:118-125.

[34]Qiu Y, Qi Y, Lu H, et al. Does time matter? Modeling the effect of time with Bayesian knowledge tracing[A]. Proceedings of the 4th International Conference on Educational Data Mining[C]. Massachusetts: International Educational Data Mining Society, 2011:139-148.

[35]Nedungadi P, Remya M S. Incorporating forgetting in the personalized, clustered, Bayesian knowledge tracing (pc-bkt) model[A]. Proceedings of 2015 International Conference on Cognitive Computing and Information processing[C]. Piscataway: Institute of Electrical and Electronics Engineers, 2015:353-357.

[36]Nagatani K, Zhang Q, Sato M, et al. Augmenting knowledge tracing by considering forgetting behavior[A]. Proceedings of the 28th International Conference on World Wide Web[C]. New York: Association for Computing Machinery, 2019:3101-3107.

[37]Zhang K, Yao Y. A three learning states Bayesian knowledge tracing model[J]. Knowledge-Based Systems, 2018, 148:189-201.

[38]Xu Yanbo, Jack Mostow. Using logistic regression to trace multiple sub-skills in a dynamic Bayes net[A]. Proceedings of the 4th International Conference on Educational Data Mining[C]. Massachusetts: International Educational Data Mining Society, 2011:241-246.

[39]Xiong X, Zhao S, Van Inwegen E G, et al. Going deeper with deep knowledge tracing[A]. Proceedings of the 9th International Conference on Educational Data Mining[C]. Massachusetts: International Educational Data Mining Society, 2016:545-550.

[40]Wang F, Liu Q, Chen E, et al. Neural cognitive diagnosis for intelligent education systems[A]. Proceedings of the AAAI Conference on Artificial Intelligence[C]. Palo Alto: Association for the Advancement of Artificial Intelligence, 2020:6153-6161.

All Roads Lead to Rome: Cognitive Diagnosis and Knowledge Tracing——A Comparison of Two Modeling Methods for Mainstream Learners’ Knowledge State

DAI Jing GU Xiao-qing[Corresponding Author]JIANG Bo

The modeling of learners’ knowledge state is one of the important tasks to build a personalized learning system. At present, there are two main mainstream methods for modeling learners’ knowledge state, namely the cognitive diagnosis method proposed by experts in the field of psychometrics and the knowledge tracking method proposed by experts in the field of human-computer interaction. In order to more properly apply the two methods to the field of intelligent education, this paper focused on the four issues of what to model, how to model, what the result is, and how to apply, discussed and compared cognitive diagnosis and knowledge tracking methods from four aspects of the scalability of input dimensions, the adaptability of modeling parameters, the refinement of output results, and the assistance of personalized recommendation services. In conclusion, the cognitive diagnosis was suitable for static evaluation and was more refined and diversified in terms of output results, while the knowledge tracking model was suitable for dynamic prediction and was more scalable in terms of input dimensions. Through research, this paper hoped to provide reference for researchers to apply these two methods reasonably to serve the personalized learning system.

learner modeling; knowledge state; cognitive diagnosis; knowledge tracing

G40-057

A

1009—8097（2022）04—0088—11

10.3969/j.issn.1009-8097.2022.04.010

基金項目：本文受上海市“科技創新行動計劃”人工智能科技支撐專項“教育數據治理與智能教育大腦關鍵技術研究及典型應用”（項目編號：20511101600）資助。

戴靜，在讀博士，研究方向為學習分析與計算機測評，郵箱為925613528@qq.com。

2021年7月30日

編輯：小時