光纖光柵液體雙參量傳感器增敏設計

華子明，李永倩*，王少康，溫芳芳，范海軍

(1.華北電力大學 電子與通信工程系，保定 071003；2.華北電力大學 河北省電力物聯網技術重點實驗室，保定 071003；3.華北電力大學 保定市光纖傳感與光通信技術重點實驗室，保定 071003)

引 言

傳統的液體溫度與壓力檢測，以較高精度、連續檢測的電子傳感器居多，其檢測信號都是基于電信號[1]，因此該類傳感器極易受電磁干擾(electromagnetic interference,EMI)影響，且將其長期置于液體環境中測量會出現參量不穩定等現象[2]。而基于光纖光柵的液體傳感器具有抗電磁干擾、耐腐蝕、準分布式測量、實現穩定和準確測量等優點，受到了國內外學者的廣泛關注和研究[3-4]。光纖布喇格光柵(fiber Bragg grating,FBG)對應變和溫度變化敏感，由于裸光柵易折斷，需有效地保護封裝后方可應用于工程項目中[5]，但封裝在一定程度上阻礙了光柵對外界參量的感知，從而影響傳感器的使用場合、測量范圍以及測量精度等。因此,設計實用化且靈敏度高的液體溫度與壓力雙參量傳感器成為近年來的研究熱點[6-10]。2017年，LIANG等人[11]提出了一種以膜片和懸臂梁為傳感單元的光纖光柵壓力傳感器，該傳感器的兩個光纖光柵分別粘貼在懸臂梁的上表面和下表面，利用兩個光纖光柵的中心波長偏移差作為測量信號，雖然提高了壓力測量靈敏度，但該傳感器封裝不夠穩定、易引入應力，且結構復雜不易加工。2020年，VENKATA等人[12]設計并制作了一種膜片式FBG傳感器，利用膜片的變形來感知液體的壓力，獲得液位的變化，然而當被測壓力超過一定限度時，膜片就會出現明顯的彎曲，光柵粘貼部分的變形較為復雜，測量精度難以保證。2020年，LIU等人[13]將兩個光纖光柵以不同的形式封裝在聚合物中，根據聚合物在特殊約束條件下浸入液體中的變形原理，可以得到液體中的壓力信息，靈敏度得到了較大的提升，但聚合物封裝的傳感器易老化，且容易出現啁啾現象。

針對上述傳感器存在的不足，本文中提出了一種基于光纖光柵的薄壁圓筒式高靈敏度溫度與壓力傳感器，該傳感器保留了薄壁圓筒式傳感器測量范圍大、精度高等優點，克服了靈敏度較低的缺點。通過仿真實驗測得，此傳感器的壓力靈敏度可達153.5pm/MPa，溫度靈敏度達31.7pm/℃。該傳感器具有低成本、耐腐蝕、可重復性好以及壽命長等特點，在壓力和溫度測量方面具有應用價值。

1 FBG傳感原理

由光源發出的一束光進入光柵后，滿足布喇格反射條件的光被反射，該反射光的中心波長為λB，其余光透射過光柵，其作用實質是在光纖中形成一個窄帶濾波器[14]。

由耦合模理論可知，滿足光纖布喇格條件的光柵反射中心波長為[15]：

λB=2neffΛ

(1)

式中，λB為布喇格光柵反射波中心波長，neff為纖芯的有效折射率，Λ為光柵周期。

由(1)式可知，有效折射率和光柵周期是影響反射波中心波長的主要因素。當溫度和壓力等外界因素發生變化時，導致有效折射率和光柵周期發生變化，從而引起反射波中心波長偏移[16]。溫度和應變的變化對FBG中心波長偏移的影響可以表示為[17]：

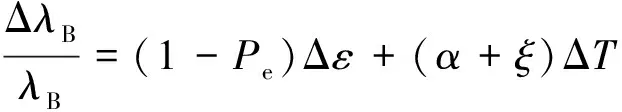
(2)

式中，ΔλB為反射波中心波長偏移量，Δε為應變變化量，ΔT為外界溫度變化量，Pe為有效彈光系數，α和ξ分別為光纖熱膨脹系數和熱光系數。本文中使用的光纖參量取自普通低損耗單模光纖，其參量初始值如表1所示。

Table 1 Initial values of optical fiber parameters

1.1 FBG反射波長與溫度的關系

由(2)式可知，在不受到外界應力的影響時，溫度變化導致反射波長變化可以表示為：

(3)

由(3)式和表1中的參量，可以得到裸光柵的溫度系數(即溫度靈敏度)為11.2pm/℃。

在工程測量中，該溫度靈敏度過低，為了提高靈敏度，可以將裸光柵粘貼在熱膨脹系數較大的基底材料上。FBG粘貼在基底材料上，當溫度發生變化ΔT時，傳感光柵產生的應變為[18]：

εT=(αg-α)ΔT

(4)

式中，αg為基底材料的熱膨脹系數。此時傳感器的波長偏移量為[19]：

ΔλB=λB[(1-Pe)(αg-α)+(α+ξ)]ΔT

(5)

由(5)式可知，溫度變化時，FBG的波長偏移量不僅與自身熱膨脹系數和熱光效應有關，而且還與基底材料的熱膨脹系數有關[20]。除金屬材料作為基底之外，也可以通過聚合物封裝FBG來提升傳感器溫度靈敏度，參考文獻[21]和參考文獻[22]中分別用環氧樹脂和苯偶酰二甲基縮酮(benzil dimethyl ketal,BDK)涂覆封裝FBG，實驗測得溫度靈敏度分別為48pm/℃和149pm/℃，相對于裸光柵而言，兩種FBG的靈敏度分別提升了4.3倍和13.3倍。因此,將光柵粘貼在膨脹系數較大的金屬材料或通過聚合物封裝后，可以有效提高光柵的溫度靈敏度。

1.2 FBG反射波長與壓力的關系

當光纖光柵處于穩定的溫度場時，如果光柵發生了應變，光柵周期和折射率也會發生變化，從而引起中心波長的偏移可以表示為：

(6)

根據(6)式和表1中的參量，可得到裸光柵的應變系數為1.2pm/με。

在工程測量時，光柵因其易折斷，不能直接用于外界壓力的測量，而是需要通過將外界壓力轉化為封裝形變進而引起光柵產生應變來實現對外界壓力的實時測量。對于薄壁圓筒封裝結構的傳感器來說，液體通過進水口進入內筒，筒壁內外兩側形成壓差，使粘貼在薄壁上的光柵產生應變，導致光柵的反射波中心波長發生偏移，由廣義胡克定律推導得到薄壁圓筒的徑向應變ε可表示為[23]：

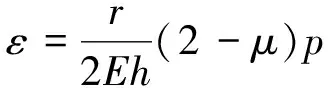
(7)

式中，E為材料的楊氏模量，μ為材料泊松比，r為內筒半徑，h為內筒壁厚度，p為液體壓力。由(7)式得出結論：傳感器內筒徑向應變與內筒半徑呈正相關，與內筒壁厚度成反比關系。將(7)式代入(6)式得：

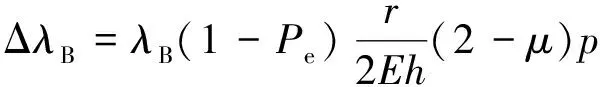
(8)

由(8)式可得出波長偏移量與液體壓力的關系：傳感器半徑越大、內筒厚度越小，材料的楊氏模量越小、泊松比越小，中心波長偏移量就越大，即傳感器的壓力靈敏度越大。

2 傳感器設計與仿真分析

2.1 傳感器設計

為了有效感應液體的溫度和壓力，需要設計合理的傳感器結構，從而將液體的溫度和壓力轉化為光柵的溫度和應變，本文中提出了一種薄壁圓筒式傳感器，如圖1所示。利用Solidworks軟件進行建模，傳感器由外殼和內筒兩部分構成，傳感器外殼長80mm，直徑30mm，壁厚1mm；類似“啞鈴”形狀的內筒由一個薄壁圓筒和位于其兩端的柱體組成，液體通過進水孔導入內筒腔，使其發生形變，從而使纏繞并粘貼在內筒壁上的光柵產生應變。同時，液體的溫度通過外殼傳導至粘貼在導溫臺的光柵上，實現壓力與溫度雙參量傳感。其中，兩個光柵串聯熔接，根據粘貼于薄壁圓筒的位置不同，分為測壓光柵和溫補光柵。將光纖從傳感結構的右側尾纖保護套接入，經過通道1后，沿著內筒的外壁緊密纏繞并將測壓光柵粘貼于內筒的外壁，光纖再穿過通道2，將溫補光柵粘貼在左側隔絕應力且具有高膨脹系數的導溫臺上，此處光柵只受溫度影響。

Fig.1 Sensor structurea—sensor profile b—sensor housing c—profile of inner tube

2.2 仿真與分析

針對于本傳感器的工作環境，傳感器的有限元分析主要集中在靜態力學分析、結構動力分析、靜態熱分析等，主要涉及通用的運動方程可以表示為[24]：

M·x+C·x+K·x=F(t)

(9)

式中，M是質量矩陣，C是阻尼矩陣，K是剛度系數矩陣，x是位移矢量，F是力矢量。熱分析主要研究溫度場，通過熱分析可以得到不同溫度下模型的溫度場，進而轉變為模型的形變和應變。通用熱方程可以表示為：

c(T)·T+κ(T)·T=Q(t,T)

(10)

式中，t是時間，T是溫度矩陣，c是比熱容矩陣，κ是導熱系數矩陣，Q是熱流率載荷向量。經過有限元分析可以求得傳感器的形變和應變等結果，進而得到傳感器的輸出特性以及傳感器的應變分布，能夠為本傳感器的靈敏度分析提供數據支撐。

設置內筒的材料、半徑、厚度、腔長以及環境溫度為變量，在ANSYS Workbench仿真軟件中使用靜態力學分析等模塊對傳感器結構進行仿真分析，研究上述變量對傳感器壓力和溫度靈敏度的影響，從而確定傳感器結構的各個參量。

仿真過程為：(1)利用Solidworks軟件設計該傳感器3-D模型；(2)將傳感器模型導入到ANSYS Workbench軟件；(3)選擇靜態力學分析模塊，設置模型材料，本仿真的材料分別為304不銹鋼與鈹青銅C17200；(4)設置網格精度進行有限元網格劃分；(5)施加載荷并進行求解；(6)通過MATLAB軟件對所有仿真結果進行圖像繪制并分析。

2.2.1 傳感器內筒材料的選擇 考慮到傳感器需在液體中長期工作，初步選擇耐腐蝕性良好的304不銹鋼和鈹青銅C17200作為傳感器材料，相關參數如表2所示。

Table 2 The related parameters of material

為了研究兩種不同材質內筒的應變的變化量，對傳感器內筒進行應變仿真。將環境溫度設置為40℃，選用厚度均為0.5mm的304不銹鋼與鈹青銅C17200材質的傳感器內筒，在其內壁施加1MPa～12MPa的壓力載荷，對數據進行線性擬合，得到徑向應變與壓力的關系如圖2a所示。由圖2a可知，在厚度一定的情況下，隨著壓力的增大，內筒壁徑向應變呈現線性增大趨勢，經擬合后得到304不銹鋼材質的傳感器應變的變化量為99.3με/MPa，鈹青銅C17200材質的傳感器應變的變化量為136.6με/MPa，故鈹青銅C17200材質的內筒徑向應變更靈敏。

為了檢驗本傳感器在不同壓強下的最長工作時間，對傳感器內筒進行壽命仿真。壽命含義為該結構在低于靜態極限強度載荷的重復載荷作用下，出現斷裂破壞現象的時間。該傳感器的壽命是通過ANSYS Workbench軟件中靜態力學分析模塊的疲勞工具仿真得到，以美國機械工程師協會 (American Society of Mechanical Engineers,ASME)鍋爐和壓力容器規范(ASME boiler and pressure vessel code)作為計算依據。

Fig.2 Relationship between sensor performance and pressure

由于傳感器內筒疲勞損傷具有隨機性和不可逆的特點，總損傷量是若干次損傷量的線性累加，采用Miner累積疲勞準則，最終完成內筒壽命的預測。在累計疲勞準則中，材料失效的臨界疲勞損傷D=1，當不同載荷施加到傳感器內筒壁上時其疲勞壽命會發生變化，隨著使用時間的增加，疲勞累計損傷可以表示為：

(11)

式中，I為疲勞損傷次數，ni為不同負載的循環次數，Ni為不同負載下應力循環次數，Wi為不同負載下吸收的能量值，W為失效總能量。

在疲勞工具模塊中應選擇應力疲勞的分析方式，選用厚度均為0.5mm的304不銹鋼與鈹青銅C17200材質的薄壁圓筒，在其內壁施加1MPa～12MPa的壓力載荷，分析兩種材質內筒結構在不同壓強下最長工作時間。對壽命仿真數據進行擬合，得到圖2b所示的壽命與壓力的變化關系。由圖2b可知，當壓力載荷施加大于11MPa(等效于水下1100m)時，304不銹鋼材質的內筒壽命突減，說明此時傳感結構已受到破壞，不能正常工作，但當304不銹鋼材質的內筒壁厚改為0.6mm時，傳感器壽命在大于11MPa不再發生突變。因此，改變傳感器的內筒材料和壁厚度便可以改變靈敏度和測量范圍，以適應不同的測量環境和要求。

2.2.2 傳感器內筒半徑的選擇 將環境溫度設置為40℃、內筒材料分別設置為304不銹鋼和鈹青銅C17200，固定內筒壁厚度和內筒腔長不變，對內筒半徑取不同值進行仿真，探究內筒半徑對徑向應變的影響。考慮到傳感器的尺寸不宜過大，故半徑范圍從5mm以1mm為步長增加到10mm，對內筒壁施加12MPa的壓力載荷。對數據進行線性擬合，得到徑向應變與內筒半徑的關系如圖3所示。

Fig.3 Relationship between strain and inner cylinder radius

由圖3可知，在內筒壁厚度和內筒腔長固定不變的情況下，隨著內筒半徑的增大，應變呈線性增大，仿真數據擬合結果與(7)式的結論一致，且鈹青銅C17200材質的內筒應變更靈敏。在筒壁彈性形變可恢復范圍內，為了尋求更高靈敏度,可以將內筒半徑設置得更大一些，但是傳感器外殼的尺寸又直接限制了內筒半徑不可能過大。綜合考慮，傳感器內筒半徑選取為10mm。

2.2.3 傳感器內筒壁厚的選擇 內筒壁厚度會影響傳感器的靈敏度，厚度太大會導致靈敏度過低，厚度太小會導致傳感器在高壓狀態下不能長期工作，所以厚度直接關系到靈敏度大小與傳感器工作壽命長短。為了尋找內筒壁厚的最優值，內筒材料分別設置為304不銹鋼和鈹青銅C17200，在內筒半徑和內筒腔長不變的情況下，環境溫度設置為40℃，對內筒厚度進行調整，范圍從0.5mm～1.0mm，步進為0.1mm，對內筒壁施加12MPa的壓力載荷，分析內筒壁厚對徑向應變的影響。通過對數據進行二次擬合，得到徑向應變與內筒壁厚的關系如圖4所示。

由圖4可知，在內筒半徑和內筒腔長固定不變的情況下，隨著厚度不斷增大，兩種材質的內筒應變與厚度均呈現負相關，且逐漸趨于平緩，仿真數據擬合結果與(7)式的結論相符，但鈹青銅C17200材質的內筒應變更靈敏。根據圖2b可知，厚度為0.5mm時，304不銹鋼材質的內筒長期工作在12MPa下，壽命明顯小于鈹青銅C17200材質的傳感器。由此可見，當內筒材料為304不銹鋼時，壁厚應選擇0.6mm；當內筒材料為鈹青銅C17200時，壁厚應選擇0.5mm。

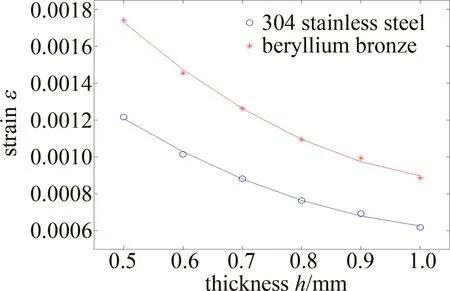
Fig.4 Relationship between strain and wall thickness of inner cylinder

2.2.4 傳感器內筒腔長度的選擇 在內筒壁厚度和內筒半徑不變的情況下，改變內筒腔長度取值，長度范圍由15mm以5mm為步長增加到35mm。內筒材料分別設置為304不銹鋼和鈹青銅C17200，環境溫度設置為40 ℃，對內筒壁施加12MPa的壓力載荷。對數據進行擬合，得到徑向應變與內筒腔長度的關系如圖5所示。

Fig.5 Relationship between strain and length of inner cylinder cavity

由圖5可知，在內筒半徑和內筒壁厚固定不變的情況下，隨著腔長不斷增大，兩種材質的內筒應變變化不明顯，故內筒腔長的變化不會對應變造成影響，仿真數據擬合結果與(7)式所得結論一致。在應變相同的情況下，選擇較長腔長的內筒，便于光纖纏繞與光柵的粘貼，但傳感器整體結構又限制了內筒腔長不宜過長。因此，傳感器內筒腔長應為30mm。

2.3 仿真結果與誤差分析

2.3.1 仿真結果 結合以上仿真結果，當傳感器內筒半徑為10mm、長度為30mm、內筒材料選擇304不銹鋼時，內筒壁厚度為0.6mm;當材料選擇鈹青銅C17200時，內筒壁厚度為0.5mm。若傳感器采用0.6mm的304不銹鋼內筒時，由表2可知，楊氏模量E=190GPa，泊松比μ=0.3，代入(8)式可得測壓光柵的理論壓力靈敏度為108pm/MPa；若傳感器采用0.5mm的鈹青銅C17200內筒時，由表2可知，E=134GPa，泊松比μ=0.275，代入(8)式可得測壓光柵理論壓力靈敏度為155pm/MPa。

圖6所示為光柵的反射波長隨壓力變化曲線。由圖6可知，反射波長與壓力呈現良好的線性關系。當內筒材料選擇304不銹鋼時，仿真壓力靈敏度為101.6pm/MPa；當內筒材料選擇鈹青銅C17200時，仿真壓力靈敏度為153.5pm/MPa，相較于裸光柵的壓力靈敏度3pm/MPa[25]分別提升33.9倍和51.2倍。

Fig.6 Relation between reflection wavelength and pressure

由表2可知，304不銹鋼和鈹青銅C17200的熱膨脹系數分別為16×10-6/℃和17.6×10-6/℃，根據(5)式可以得到兩種材質的傳感器溫度靈敏度分別為29.9pm/℃和31.8pm/℃。對兩種材質傳感器進行溫度靈敏度分析，溫補光柵在不受任何應變的情況下，對外界溫度進行調整，范圍-5℃～40℃，步進為5℃，溫補光柵區域反射波長隨溫度的變化如圖7所示。

Fig.7 Relation between reflection wavelength and temperature

由圖7可知，測溫光柵反射波長隨溫度變化呈現良好的線性關系，當傳感器材料采用304不銹鋼時，溫度靈敏度可達30pm/℃，約為裸光柵的2.6倍；當傳感器材料采用鈹青銅時，溫度靈敏度可達31.7pm/℃，約為裸光柵的2.8倍。

2.3.2 誤差分析 本傳感器的壓力和溫度仿真靈敏度與(5)式和(8)式計算得到的壓力和溫度理論靈敏度對比可知，當傳感器內筒材料為304不銹鋼時，壓力靈敏度的相對誤差為5.92%，溫度靈敏度的相對誤差為0.33%；當傳感器內筒材料為鈹青銅C17200時，壓力靈敏度的相對誤差為0.96%，溫度靈敏度的相對誤差為0.31%。針對304不銹鋼材質的傳感器壓力靈敏度誤差較大的問題，經過反復驗證得出結論：在有限元分析時，對同一個模型進行不同大小網格劃分以及不同形狀網格劃分時，會對仿真結果產生一定影響，將網格縮小至1.8mm時，壓力靈敏度的相對誤差能夠從5.92%降至0.04%；對于溫度靈敏度的誤差是由于隨著溫度的變化，金屬材料會產生微小形變，進而對波長造成微小影響。

3 結 論

為了解決現有光纖光柵液體雙參數傳感器靈敏度低等問題，結合光柵傳感原理，利用Solidworks軟件對傳感器建模，使用仿真軟件系統地分析了傳感器內筒各個參量對傳感特性的影響，為傳感器的制備提供了理論基礎。結果表明，使用304不銹鋼材料封裝的傳感器壓力靈敏度可以達到101.64pm/MPa，溫度靈敏度可以達到30pm/℃；使用鈹青銅C17200材料封裝的傳感器壓力靈敏度可以達到153.5pm/MPa，溫度靈敏度可以達到31.7pm/℃，并對結果存在的誤差進行了評估。更重要的是，改變該傳感器的內筒材料和尺寸便可以改變靈敏度和測量范圍，以適應不同的測量環境和要求。這種雙參量傳感器在石油開采和海洋勘探等復雜環境領域有許多潛在的準分布測量應用，在液體壓力和溫度測量方面具有應用價值。