基于遺傳算法的潛器壓載敷設優化方法

唐波，楊坤，周海波，周生俊，楊振錦

1 武漢第二船舶設計研究所，湖北 武漢 430205

2 中國人民解放軍 92578 部隊，北京 100161

0 引 言

船舶的初橫穩性高是衡量其穩性的重要指標，也是保證船舶正常航行的必要航海性能[1-3]。而潛器作為一類特殊的船舶更是如此，需要同時考慮水面和水下狀態的初橫穩性高。此外，初橫穩性高的裕度還直接決定了潛器服役后可進行現代化改換裝的能力。在完成潛器總體布置和各類載荷的統計后，一般通過敷設固定壓載（常用壓載鐵[4]）來平衡固定浮容積與各類載荷間的重量差和重量矩差，并控制初橫穩性高。因此，壓載的敷設方案將對潛器的初橫穩性高產生重要影響。

傳統的壓載敷設方法是：首先根據固定浮容積與各類載荷間的差值計算出需敷設的壓載量，隨后根據各艙舷間總體布置情況，通過人為的統籌分配，在重量、縱向和橫向重量矩基本平衡的前提下，將壓載盡可能低位敷設。采用該方法存在的問題：一是工作繁瑣，人工迭代工作量巨大；二是難以保證敷設后垂向重心高度最優或是較優。特別是在壓載量大、潛器縱向尺寸長、可敷設肋位多的情況下，上述問題將更加突出。因此，研究滿足壓載敷設需求且總體重心較低的優化方法十分有必要。

現行標準[5]和工程參考書目規定了固定壓載總量的計算方法，以及試潛定重后調整的要求，同時還提出了將壓載盡量敷設于龍骨底部附近，壓載重心縱向位置應位于船舯前后1/6 艇長范圍內等原則要求，卻未提出全船固定壓載敷設的具體方法與指導方針。陳靜等[6]研究了優化算法在船舶壓載水置換方案中的應用，但壓載水置換的目的（主要為環保）及其數學建模、優化目標等與潛器的固定壓載敷設完全不同，屬于不同領域的問題。黃文華等[7]提出了采用壓載鉛代替壓載鐵的技術方向，即利用鉛與鑄鐵的密度差來縮小同質量壓載的體積需求，以獲得更好的初橫穩性高，但選用密度更大的壓載鉛距離將其廣泛應用于潛器還存在一些實際困難，如防腐涂層設計、鉛的毒性影響等，且其對穩性高的具體貢獻也有待詳細計算。當然，無論是選用何種材料的固定壓載，工程上迫切需求的仍是一種指導性的方法，即通過優化壓載布置來得到重心較低的敷設方案。而在該方面，國內外尚無相關的文獻資料，在目前的工程實踐中，潛器的固定壓載敷設仍然是依靠大量的人工迭代來獲得。

為此，本文將首先研究潛器固定壓載敷設的橫剖面特征，構建潛器壓載敷設的數學模型，提取壓載敷設的目標函數和約束函數，隨后運用智能優化算法得到優化的敷設方案，最后通過計算不同約束參數算例，驗證方法的可行性，以獲取一些對工程實際具有重要意義的壓載敷設原則來供科研和設計人員參考。

1 計算方法

運用智能優化算法對固定壓載進行敷設，其關鍵技術包括建立固定壓載敷設的數學模型以及提取壓載敷設的目標函數和約束函數這2 個方面。

1.1 壓載敷設優化數學模型

圖1 所示為簡化的潛器模型，其中x方向為潛器縱向，向艏為正，原點為耐壓殼體艏艉長度中心點；z方向為潛器垂向，向上為正，過耐壓殼體圓心，原點為輕殼體最低點；y方向為潛器橫向，向右舷為正。

圖1 典型雙殼體潛器壓載敷設簡化模型Fig. 1 Typical simplified model of a double-hull submersible with kentledge

在敷設壓載前，潛器的固定浮容積為V0，固定浮容積產生的縱向力矩為MVX， 橫向力矩為MVY，垂向力矩為MVZ。除壓載外，其他各類載荷產生的重量為W0，對應產生的縱向力矩為MX，橫向力矩為MY，垂向力矩為MZ。可供敷設的壓載共有N個檔位，其中第i個檔位敷設的壓載重量為Wi（空氣中重），此檔位置處壓載合計的重心為縱向Xi，橫向Yi，垂向Zi。壓載敷設應滿足的約束條件包括重量、縱向力矩和垂向力矩3 個方面。在重量上，壓載應平衡固定浮容積與其他載荷的差值：

在縱向上，壓載應平衡固定浮容積與其他載荷產生的縱向力矩的差值：

在橫向上，壓載應平衡固定浮容積與其他載荷產生的橫向力矩的差值：

式（1）～式（3）為約束函數，其中 ρYZT為壓載密度， ξW，ξX，ξY均為一小值。水下初橫穩性高h[8]為

式中：r為橫穩心半徑；c為自由液面修正系數。考慮到敷設壓載后壓載整體對潛器的浮心和重心均會產生一定的影響，為簡化問題，將目標函數簡化為壓載總體重心最低，即目標函數可以寫作

為求得每一檔位的重量值Wi和 重心高度Zi，需對壓載敷設進行數學簡化。每檔可敷設壓載位置的橫剖面如圖2（a）和圖3（a）所示，即壓載的各層累積填充于底部或舷間下部區域。通過類比，每一塊壓載相當于有限元法中的“六面體單元”，由于這些“單元”尺寸小，且實際間隙可忽略不計，采用逆向思考，可將這些離散的“單元”壓載組合看做一個連續的整體或液體，“充滿”了可敷設區域。

圖2 典型雙殼體潛器舷間敷設壓載簡化模型1Fig. 2 Typical simplified model-1 of a double-hull submersible with kentledge

圖3 典型雙殼體潛器舷間敷設壓載簡化模型2Fig. 3 Typical simplified model-2 of a double-hull submersible with kentledge

壓載的上邊緣亦有多種情形，需討論后進行簡化。圖4 所示為2 種情況下的上邊緣，其中圖4（a）情形下壓載的合計重心高度為G1，圖4（b）情形下壓載的合計重心高度為G2，考慮到“液體總是在最低勢能處靜止”, 因此，在體積V相同的前提下，圖4（a）中重心G1較 圖4（b）中重心G2更低。實際上，圖4（a）所示頂部水平的情形為重心最低的唯一情形，后續將在簡化模型中采用此上邊緣形式進行計算。

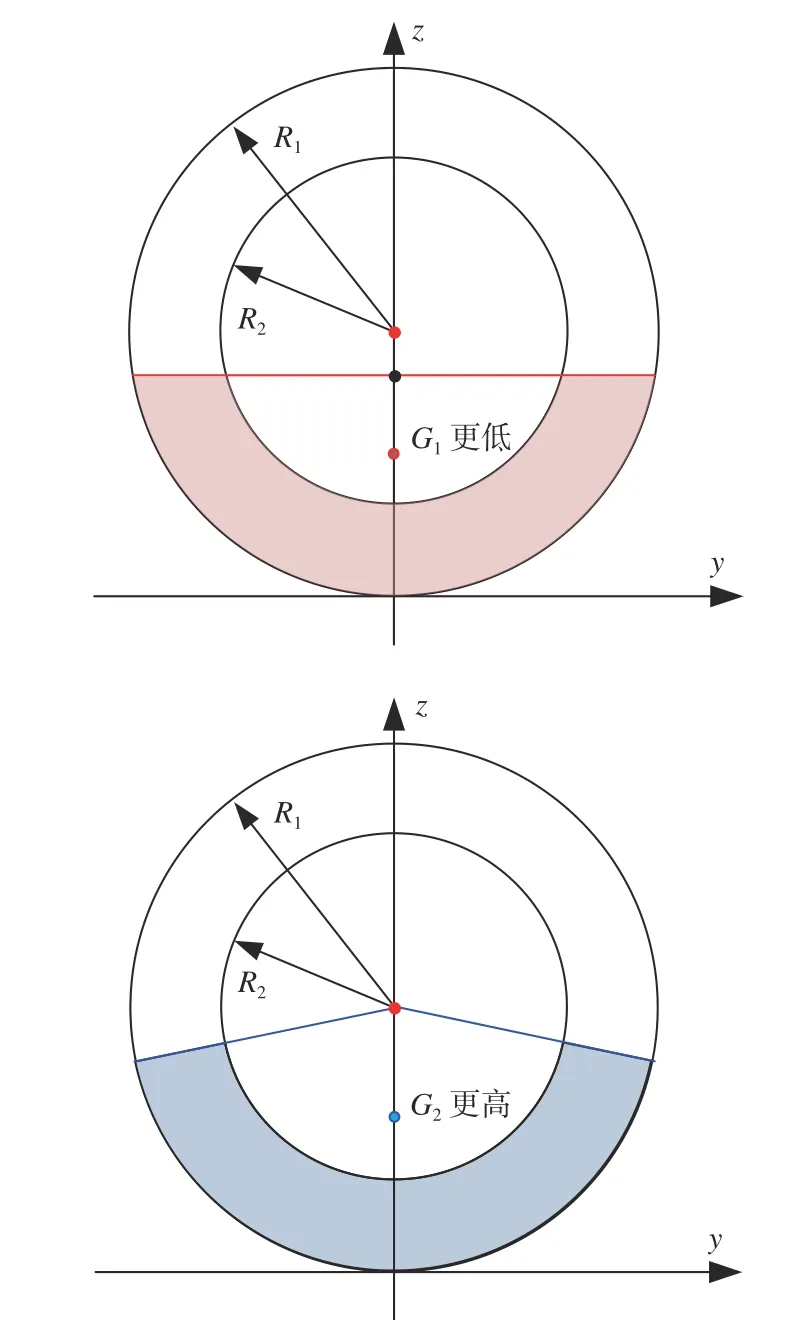
圖4 兩種舷間敷設壓載形式的高度差別Fig. 4 Gravity center difference of two simplified fixed kentledge models

因此，可將壓載敷設情況簡化為如圖2（b）和圖3（b）所示的函數模型。其中，圖2（b）為壓載邊界上限較低，未超過耐壓殼體肋骨下邊緣的情形；圖3（b）為壓載邊界上限相對較高，超過耐壓殼體肋骨下邊緣的情形。在圖2（b）和圖3（b）中，壓載敷設邊界區域的橫坐標可以表示為垂向坐標的函數。對于內邊界，在y≥0區 域，設y=F(z)，該函數代表耐壓殼體外肋骨邊界的圓弧線，該圓弧線的半徑為R2； 而在y≤0區 域，y=-F(z)。對于輕殼體邊界，在y≥0區 域，設y=G(z)，該函數代表輕殼體邊界的圓弧線，該圓弧線的半徑為R1；而在y≤0區 域，y=-G(z)。

根據以上假設，在圖2（b）所示簡化模型中，壓載上邊緣與輕殼體在第1 象限交點的橫坐標可以表示為Yi0=G(Zi0)；在圖3（b）所示簡化模型中，壓載上邊緣與耐壓殼體肋骨、輕殼體在第1 象限交點的橫坐標可以表示為Yi0=F(Zi0)，Yi1=G(Zi0)。

針對圖2（b）中壓載部分，其截面積為

對應的重心高度為

針對圖3（b）中壓載部分，其截面積為

對應的重心高度為

在特殊情況下，若因總體布置等限制，導致壓載在左右舷不對稱敷設（圖5），則其在左舷的面積和重心高度分別為：

圖5 典型雙殼體潛器舷間敷設壓載簡化模型3Fig. 5 Typical simplified model-3 of a double-hull submersible with kentledge

同時，還需要考慮左舷重心橫向位置：

在右舷，對應的結果分別為：

則敷設此檔位處壓載所產生的重量值為：

式中，d為此檔位處壓載在縱向上的長度尺寸。

1.2 遺傳算法

如上節所述，每檔位處壓載的重量和重心高度并非為連續函數，且考慮到壓載敷設的檔位較多，擬采用遺傳算法來作為尋優的優化算法。遺傳算法于1962 年由John Holland 提出，算法中引進了群體、適應值、選擇、變異、交叉等基本概念，以應用于函數優化，主要具備以下優點[9]：

1） 遺傳算法以參數的編碼集作為運算對象，其在搜索的過程中不受優化函數連續性及其導數求解的限制，因而具有很強的通用性；

2） 遺傳算法直接使用由目標函數確定的適應度函數信息，以群體為單位執行搜索過程，可以較快地搜索到適應度較好的搜索空間，因而具有較強的全局搜索能力。

遺傳算法的流程如圖6 所示[10]。

圖6 遺傳算法流程圖Fig. 6 The flow chart of genetic algorithm

2 計算方法

2.1 算例模型

首先，為驗證基于遺傳算法的固體壓載敷設優化方法的可行性和普遍適應性，選取了表1 中所示較為寬泛的壓載重量、需提供的縱向和橫向力矩以及檔位數量等參數范圍來進行仿真計算。

表1 寬范圍算例模型參數表Table 1 The model parameters of examples with wide variation

隨后，通過控制變量，研究壓載重量、需提供的縱向和橫向力矩、檔位數量、是否左右對稱敷設等不同參數變化對優化結果的影響，然后通過觀察每一參數的優化趨勢，對實際敷設提出指導性意見。具體的控制變量算例如表2 所示。

表2 控制變量算例模型參數表Table 2 The model parameters of controlling variables for calculation examples

控制遺傳算法的主要參數設置參見表3。

表3 遺傳算法主要參數設置Table 3 The parameter setting of genetic algorithm

2.2 結果分析

1） 優化方法的可行性分析。

通過構建數學模型，提取目標函數和約束函數，并結合遺傳算法進行優化計算，得到表1 中各算例的壓載敷設結果如圖7 所示。由圖可見：

圖7 寬范圍算例下各檔位左右舷壓載敷設高度優化結果Fig. 7 The optimization results of kentledge laying height at the left/right side in the calculation examples with wide parameter variation

（1） 在不同壓載重量、需提供的縱向和橫向力矩，以及檔位數量等參數條件下，采用本文所提的建模和遺傳優化方法均能得到優化結果，且在不同參數下，優化結果均是以一種“梯度”的趨勢去平衡力矩的，證明該方法可行且適用。

（2） 在檔位較少的情況下，如算例1，2，3，各檔位“梯度”的一致性較好；在檔位較多的情況下，如算例4，出現了多處局部不符合一致的“梯度”現象。經分析，檔位數的增加即轉化為變量數的增加，需同步增加遺傳算法中種群的數量才能得到更好的結果，但同樣也將增加計算時間。

同時，對表2 中控制變量的各算例進行計算，結果如圖8 所示。由圖可見，在各參數下均能通過遺傳算法得到優化結果。針對每一算例，選取20 次優化計算的最好值進行后續的對比分析。

圖8 控制變量各算例優化計算結果對比Fig. 8 Comparison of optimization result of controlling variables for calculation examples

2） 同一算例不同優化結果的原因分析。

如圖9 所示，針對算例5 的20 次優化計算結果，選取最好和最差的結果（相當于一般的人工迭代方案）進行對比，研究相同約束條件下壓載重心高度的影響因素。由圖9（a）可看出，兩結果均呈艉部少、艏部多的敷設規律，這樣可以平衡給定的縱向力矩（在敷設壓載前，潛器艉部較重）。但同時也觀察到，較好算例各檔位之間梯度較小，壓載重心低；而較差算例的梯度則明顯較大，導致壓載重心較高，較好算例的壓載重心比較差算例約低23%。因此，在保證平衡縱向力矩的前提下，為了降低壓載重心，應以較小的“梯度”去敷設。3） 敷設檔位數量對優化結果的影響分析。

圖9 各檔位下左右舷較好和較差壓載敷設計算結果對比（算例5）Fig. 9 The best and worst left/right side kentledge laying height results comparison of example 5

如圖10 所示，選取算例5 和算例6 的最好結果，研究在其他約束相同的條件下，不同敷設檔位數量對壓載重心高度的影響。其中算例6 的敷設檔位較多，共9 檔，在進行優化時將壓載盡量均攤到了各檔位，相較于算例5 共計5 檔的敷設結果，其重心高度明顯降低。因此，在敷設壓載時，為降低壓載重心，應敷設盡量多的檔位。

圖10 左右舷壓載敷設檔位數量對優化結果的影響Fig. 10 Different amount of laying frames influence on left/right side kentledge laying height optimization

4） 縱向力矩對優化結果的影響分析。

如圖11 所示，選取算例5、算例7 和算例8 的最好結果，在其他約束相同的條件下，研究不同平衡縱向力矩對壓載重心高度的影響。由圖11（a）可以看出，算例7 需要的平衡縱向力矩最小，為10 t·m，算例8 需要的平衡縱向力矩最大，為200 t·m，優化結果為算例7 的重心最低，算例8 的重心最高。通過觀察敷設情況，分析造成此差異的原因，認為需要的平衡力矩越大，平衡力矩所產生的各檔位的敷設梯度越大，重心也越高。

圖11 縱向力矩對各檔位左右舷壓載敷設優化結果的影響Fig. 11 Different longitudinal moment influence on right/left side kentledge laying height optimization

5） 高度限制對優化結果的影響分析。

如圖12 所示，選取算例5 和算例9 的最好結果，在其他約束相同的條件下，研究某檔高度限制對壓載重心高度的影響。由圖12（a）可以看出，對于最靠近艏部的一檔，若將其壓載敷設高度限制為2 米，結果顯示，將會導致其他檔位需要采用較大梯度的平衡縱向力矩，致使其重心高度明顯高于算例5，如圖12（b）所示。可見，如果存在高度約束使固定壓載敷設無法形成一致的梯度時，壓載重心將相應增加。

圖12 高度限制對各檔位左右舷壓載敷設優化結果的影響Fig. 12 The vertical restriction influence on left/right side kentledge laying height optimization

6） 優化算法平衡橫向力矩效果分析。

算例5～算例9 在建模時即限制其為左右舷對稱敷設，而算例10 則放開了左右舷敷設高度的限制，通過算法來自行尋找最優解。算例10 需要平衡的橫向力矩為0，如圖13 所示，故其找尋到的優化解仍為左右舷對稱，且其重心也與算例5 基本相當，說明優化算法可以很好地平衡左右舷力矩。7） 橫向力矩對優化結果的影響分析。

圖13 各檔位左右舷壓載敷設優化算法平衡橫向力矩效果Fig. 13 The left/right side kentledge laying height optimization result on lateral moment

如圖14 所示，選取算例10、算例11 和算例12的最好結果，在其他約束相同的條件下，研究不同平衡橫向力矩對壓載重心高度的影響。由圖14（a）可以看出，算例10 需要的平衡橫向力矩最小，為0 t·m，算例12 需要的平衡橫向力矩最大，為100 t·m，優化結果為算例10 的重心最低，算例12的重心最高。通過觀察敷設情況，分析造成此差異的原因，認為需要的平衡橫向力矩越多，左右舷平衡力矩所產生的各檔的敷設梯度越大，重心也就越高。

圖14 各檔位左右舷不同橫向力矩壓載敷設計算結果對比Fig. 14 Different lateral moment influence on left/right side kentledge laying height optimization

3 關于應用問題的思考與討論

壓載敷設優化方法在實際工程應用中還面臨著以下2 個方面的問題：

1） 對于排水量小、縱向長度較短的潛器，以上壓載敷設尋優方法可以很好地適用；但對于排水量大、縱向敷設檔位可達上百檔的潛器，因變量數目顯著增加，導致計算仿真將消耗大量的時間。

2） 在潛器設計中，耐壓殼體與輕殼體之間的舷間往往存在一些布置區域限制因素，如舷間水道圍壁、通海閥圍壁等，在建模仿真時需要予以考慮。

3.1 多檔位敷設優化問題

針對固體壓載可敷設檔位多，同步計算資源消耗大的情況，嘗試考慮了“先粗分，后細分”的優化模式，即首先根據艙室或艙段劃分10 個以內的簡化檔位，得到第1 輪的重量優化分配后，再對每個艙室縱向范圍內的各檔肋位進行第2 輪的詳細優化分配。

圖15 所示為進行第1 輪的粗分和第2 輪細分后的優化結果。在局部“細分”過程中，每一檔為了得到最低的重心會進行等分，從而使得在全局上無法得到梯度一致的結果，因此以上方法實際上是一個“誤區”。

圖15 優化結果示意圖Fig. 15 Schematic diagram of the optimization results

綜上，針對檔位較多的情況，建議仍舊按照每檔建模、統一優化的方式進行計算；而對于優化結果可能出現的局部梯度不一致的問題，可根據“最小梯度”經驗人為地進行快速調配，以便在消耗盡量少的計算資源的情況下得到優化結果。

3.2 關于布置區域限制因素

針對有布置區域限制的情況，如圖16（a）所示，在建模時可以簡化為分段函數，簡化模型參照圖16（b）和圖16（c）。實際上，考慮到分段函數導致的建模的復雜性，其仿真將會消耗更多的計算資源，因此建議在實際應用中，在檔位較多的情況下可釋放這些限制因素，在計算完成后再自行進行人工調配，這樣亦能得到工程上可接受的結果。例如對于圖16（a）所示情況，可直接先按照如圖3（b）所示無布置區域約束的數學模型進行計算，后續再進行調配。

圖16 布置區域限制示意圖及簡化模型Fig. 16 The area restrict sketch and simplified mathematic model

4 結 語

本文基于一種離散模型連續化的逆向思維，對潛器固體壓載敷設進行數學建模，然后提取約束函數和目標函數并結合遺傳算法對固定壓載方案進行了尋優。多個算例證明，本文所提方法可行且有效：在平衡重量、縱向力矩和橫向力矩的前提下，無需人工干預，即可尋找出重心較低的壓載敷設優化方案，得到的較好算例相比較差算例（相當于人工算例）其重心下降近23%，大幅降低了人工迭代的工作量。同時，本文對不同參數條件下優化結果的分析研究，以及有關及實際應用問題的思考與討論，可供工程設計人員參考。