船舶槳軸系統的縱向雙級隔振技術

劉秀峰，李全超，周睿

1 海軍裝備部，湖北 武漢 430064

2 中國艦船研究設計中心，湖北 武漢 430064

0 引 言

船舶槳軸系統運行中產生的低頻縱向振動將激發艉部結構產生輻射噪聲，這是船舶振動噪聲控制的重點和難點。推進器通過在不均勻流場中旋轉而產生推力，其存在的交變分量將形成縱向激勵力來激勵軸系并通過軸系-推力軸承向船體結構傳遞，從而引起艉部結構振動并引發輻射噪聲。

目前，槳軸系統縱向控制領域的主要工作集中于在軸系-推力軸承推力傳遞通道上開展隔振或減振技術研究。馮國平等[1]、吳崇建等[2-3]通過分析船體艉部的縱向激勵傳遞特性，認為推力軸承基座是軸系縱向振動的主要傳遞途徑；楊志榮等[4]、游晶越等[5]、胡澤超等[6]均提出在船舶軸系上應用動力吸振器的設計思路，并分析了不同安裝方案下的動力吸振器對軸系縱向減振效果的影響；李全超等[7-9]提出了不同形式的船舶減振推力軸承設計思路，并通過理論分析和試驗研究驗證了其對軸系縱向振動的控制效果。

軸系縱向減振一般采用單級隔振的形式，將槳軸系統簡化為單自由度系統，并通過系統隔振的方式來改變槳軸系統的縱向振動特性，從而改變力傳遞特性以實現隔振目的。根據單自由度系統的隔振原理，當頻率大于倍的系統固有頻率時，系統振動傳遞率將小于1。理論上，系統的固有頻率設計值越小，其在控制頻段內的隔振效果越好。

然而，單級隔振系統的隔振傳遞率非常有限，尤其對于槳軸系統縱向二階固有頻率之外的中頻區域而言，單級隔振的應用局限性更大。廣泛應用于高精度儀器設備中的雙級隔振系統則可以實現更好的隔振性能，通過選擇適當的系統參數即可明顯提高隔振性能[10-11]。

為此，本文擬提出基于雙級隔振技術的槳軸系統縱向振動控制方案，將分析雙級隔振狀態下的振動數學模型和槳軸系統縱向振動特性，進而研究質量比、剛度比、阻尼比等設計參數對系統固有頻率比、振動傳遞率的影響，用以為船舶槳軸系統的縱向雙級隔振技術提供參考。

1 系統動力學模型

槳軸系統的推力傳遞通道即為縱向激勵力的傳遞通道，縱向雙級隔振的設計思路與單級隔振相似，都是在推力傳遞通道上設計減振結構，通過減振結構的剛度設計來控制系統的固有振動特性，從而實現振動隔離。

對于單級隔振系統，其隔振體對基座的振動絕對傳遞率T[12]為

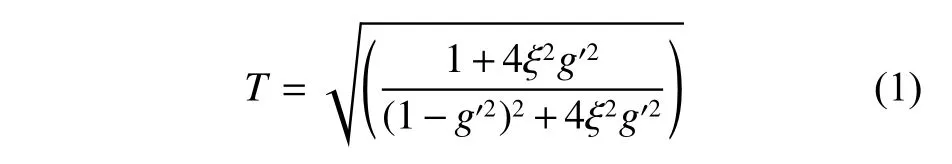
采用雙級隔振技術的船舶槳軸系統如圖1 所示，在軸段1 與軸段2 之間設置軸段減振器，在軸段2 與船體結構之間設置減振推力軸承。由于聯軸器的縱向剛度遠低于這2 組減振設備，故可忽略聯軸器與電機對槳軸系統的影響。2 組減振設備使槳軸系統變成了雙級隔振系統，其動力學模型如圖2 所示，其中：m1為軸段1 和推進器的質量；m2為軸段2 的質量；k1，c1分別為軸段減振器的縱向剛度、阻尼系數；k2，c2分別為減振推力軸承的縱向剛度、阻尼系數；F為振動激勵；x1，x2，u分別為質量m1、質量m2、基座的位移。

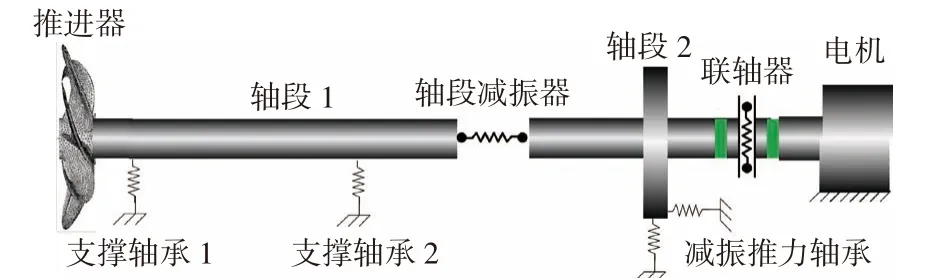
圖1 船舶槳軸系統的布置示意圖Fig. 1 Structure diagram of ship propeller-shaft system

圖2 軸系縱向雙級隔振系統模型Fig. 2 Model of ship propeller-shaft longitudinal two-stage vibration isolation system

雙級隔振系統的振動方程為

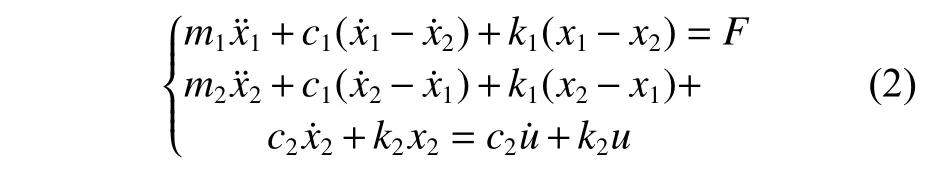
在零初始條件下，忽略阻尼影響，即可將式（2）變為無阻尼二自由度系統的自由振動方程，其系統一階、二階固有頻率 ωn1， ωn2分別為[12]

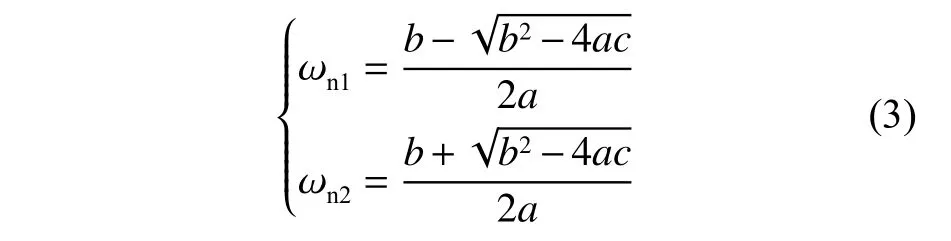
式中：b=m1k1+m1k2+m2k1；a=m1m2；c=k1k2。

設定系統的固有頻率比fn=ωn2/ωn1，質量比μ=m2/m1， 剛度比v=k2/k1， 則固有頻率比fn為

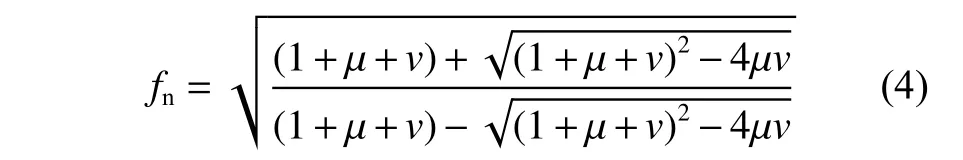
由式（4）可知，系統固有頻率比fn由質量比μ和剛度比v決定。

令 一 階 頻 率 ω1=， 二 階 頻 率

其中：

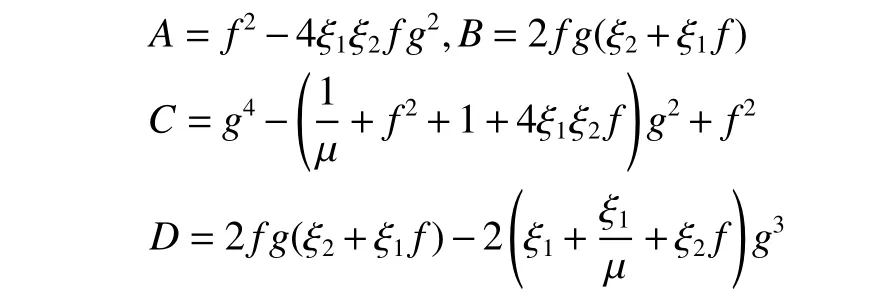
本文將采用20lg（T）來評價系統的振動絕對傳遞率。

2 系統振動傳遞特性分析

本節將以某船槳軸系統作為研究對象，取質量比μ=1、剛度比v=1、阻尼比 ξ1=ξ2=0.005，建立動力學模型，進而分析其振動傳遞特性，并將與系統總質量相同、一階固有頻率相同的單級隔振系統的振動傳遞特性進行對比分析，結果如圖3所示。為便于對比說明，本文以雙級隔振系統的一階固有頻率為基數設定頻率比，即此處頻率比g′=ω/ωn1。

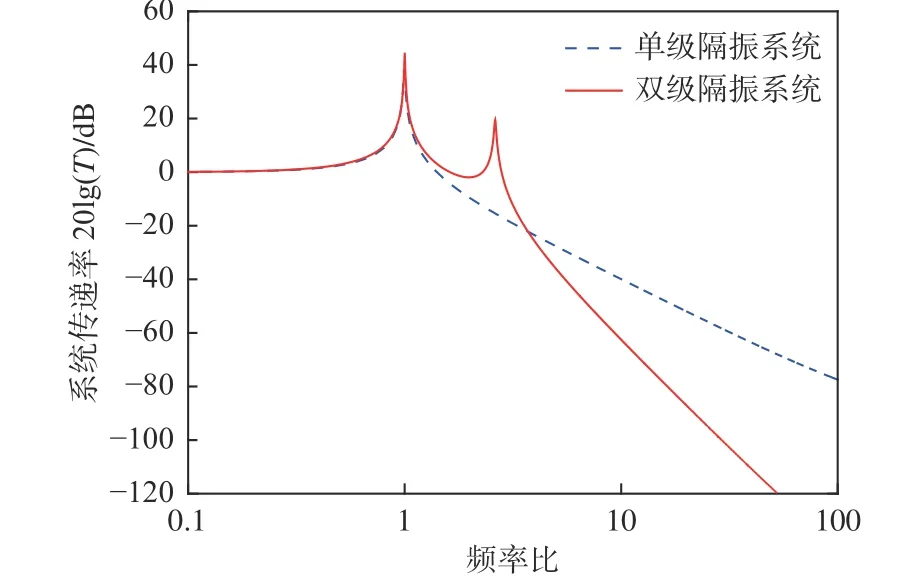
圖3 單級與雙級隔振系統的傳遞率對比Fig. 3 Comparison of transmissibility between single-stage and two-stage vibration isolation systems

從圖3 中可以看出，當槳軸系統采用雙級隔振技術之后，其振動傳遞特性中增加了一個共振頻率特征，即在新增的二階固有頻率附近出現了與一階固有頻率特征相似的共振點，但其系統振動絕對傳遞率在二階共振頻率之后則以-24 dB/oct的斜率迅速下降，遠高于單級隔振系統-12 dB/oct的斜率。由此可見，在高頻率比的中頻區域，雙級隔振系統的隔振性能優于單級隔振系統。

與單級隔振系統不同，雙級隔振裝置不再以g′＞作為系統發揮隔振功能的設計邊界，而是由系統二階固有頻率及其之后的衰減趨勢所決定。對于雙級隔振系統而言，系統固有頻率比fn的控制尤為重要，fn越低，減振效果發揮的起始頻率就越低，系統的隔振控制區域也將隨之向低頻延伸。此外，由式（5）可知，阻尼參數也會影響系統振動傳遞率的變化，尤其是共振頻率處的頻率響應衰減。

3 系統固有頻率比的影響規律

由于系統固有頻率比fn是質量比 μ和剛度比v的二元函數，所以本節將基于這2 個參數開展對比分析。圖4 所示為質量比0.01～10，剛度比0.01～10 狀態下的二級隔振系統固有頻率比變化曲面，從圖中可以看出，系統固有頻率比隨著剛度比、質量比的同步增加而呈非線性降低趨勢，且該曲面圖沿 μ-v平 面對角線與fn軸形成的垂直中心面對稱分布。由此可見，同步增加質量比μ、剛度比v即可降低系統固有頻率比fn。

圖4 質量比和剛度比對系統固有頻率比的影響Fig. 4 Influence of mass ratio and stiffness ratio on natural frequency ratio of system

3.1 質量比對系統固有頻率比的影響

剛度比一定時，二級隔振系統固有頻率比隨質量比的變化規律如圖5 所示，從圖中可以看出：

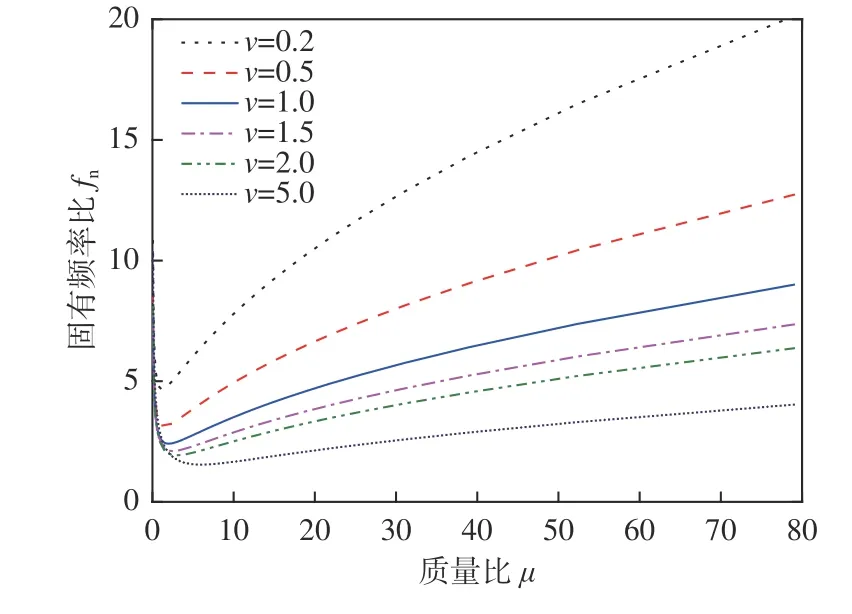
圖5 剛度比對固有頻率比的影響Fig. 5 Influence of stiffness ratio on natural frequency ratio

1） 隨著質量比的增加，系統固有頻率比呈先下降而后升高的“√”形趨勢，每條曲線都存在1 個“拐點”，該“拐點”即為系統固有頻率比的最小值。

2） 隨著系統剛度比的增加，系統固有頻率比的最小值越小，其對應的系統質量比也隨之向高點偏移。

3） 系統固有頻率比最小值處的質量比與剛度比之間存在明顯的線性關系，即

按照上述規律，可以進一步簡化式（4），當剛度比v一定時，系統最小固有頻率比fnmin為

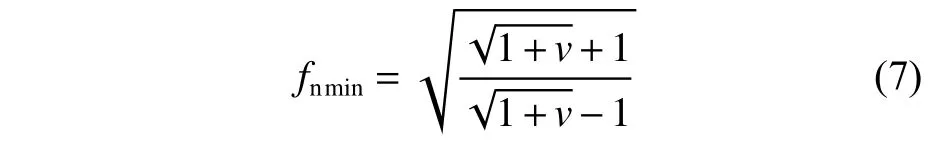
由式（5）可知，此時系統質量比恒大于1。

3.2 剛度比對系統固有頻率比的影響

當質量比一定時，二級隔振系統固有頻率比隨剛度比的變化規律如圖6 所示。由于式（4）中的質量比 μ和剛度比v具有互易性，所以圖6 的變化規律與圖5 一致，但系統固有頻率比最小值處的質量比與剛度比關系調整為

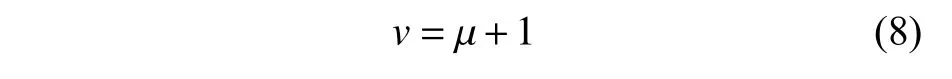
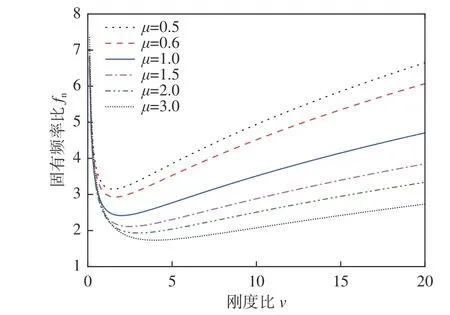
圖 6 質量比對固有頻率比影響Fig. 6 Influence of mass ratio on natural frequency ratio

同理，當質量比 μ一定時，式（4）可簡化為

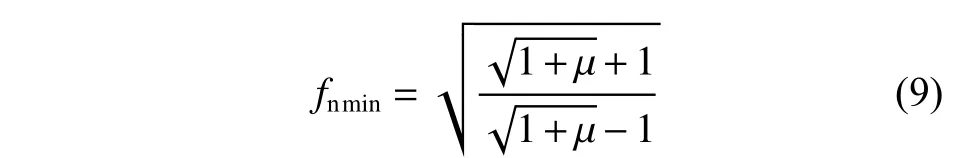
此時質量比可以控制在1 以下，而系統剛度比則恒大于1。

根據式（8）將系統固有頻率比由質量比、剛度比的二元函數優化為一元函數，并按式（9）進一步分析不同質量比狀態下的系統最小固有頻率比的變化規律，結果如圖7 所示。從圖中可以看出，質量比越小，系統最小固有頻率比隨質量比的變化越敏感：當質量比從0.01 增加到1 時，系統最小固有頻率比從20 下降至2.414；當質量比從1 增加到10 時，系統最小固有頻率比僅從2.414 下降至1.365。

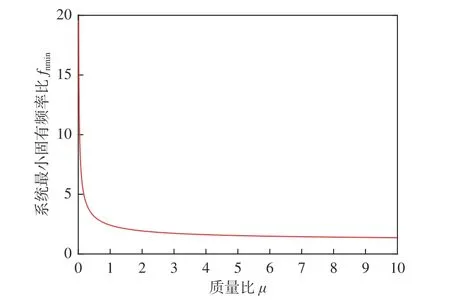
圖7 質量比對系統最小固有頻率比的影響Fig. 7 Influence of mass ratio on minimum natural frequency ratio of system

4 阻尼比對系統動態性能的影響

以第2 節中應用雙級隔振技術的某船槳軸系統作為研究對象，在其他設計參數不變的情況下，分別改變系統阻尼比 ξ1， ξ2之后的隔振系統振動傳遞特性如圖8 和圖9 所示，從圖中可以看出：

1） 阻尼比 ξ1， ξ2的增加均將導致二級隔振系統固有頻率附近的振動傳遞率有所降低，而系統二階固有頻率之后的振動傳遞率則隨之增加。

2） 不同阻尼比的雙級隔振系統的振動傳遞率曲線存在1 個相交點（圖8 的A 點和圖9 的B 點）。

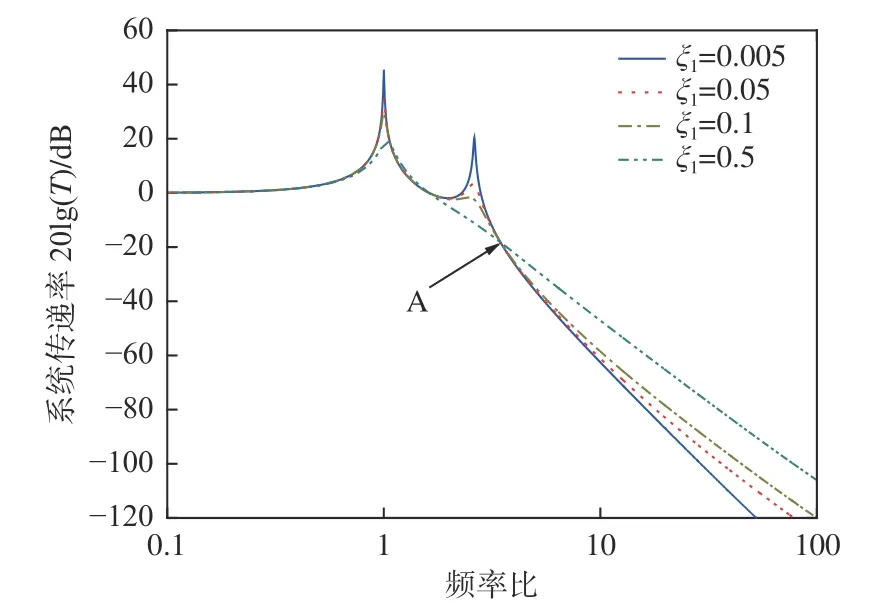
圖8 阻尼比 ξ1對系統振動傳遞率的影響Fig. 8 Influence of damping ratio ξ1 on vibration transmissibility of system

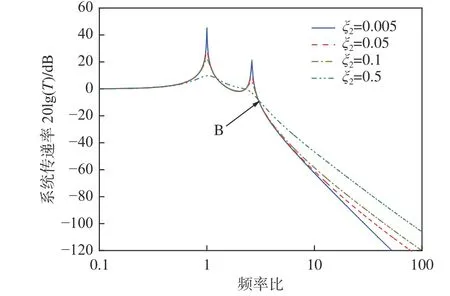
圖9 阻尼比 ξ2對系統振動傳遞率的影響Fig. 9 Influence of damping ratio ξ2 on vibration transmissibility of system

3） 當阻尼比增加時，曲線相交點之后的中高頻段的系統振動傳遞率也將隨之增加。

4） 阻尼比 ξ1， ξ2所對應的相交點并不相同。

5） 當阻尼比 ξ1增加時，系統二階固有頻率處的振動傳遞率衰減更為明顯。當 ξ1＞0.1時，其振動傳遞率小于1，即系統開始發揮隔振功能。

6） 阻尼比 ξ2對系統一階、二階固有頻率處振動傳遞率的衰減貢獻量基本相當，且不同阻尼比ξ2下的系統振動傳遞率在一階、二階固有頻率之間還存在2 個相交點（圖9）。由于系統阻尼比在實際工程應用中的可設計難度較高，故本文不再深入分析其影響規律。

5 槳軸系統的縱向雙級隔振設計優化

結合質量比、剛度比、阻尼比等參數對系統振動特性的影響規律，以某船槳軸系統為分析對象（圖10），進一步研究雙級隔振技術對其槳軸系統縱向振動的控制效果。該船槳軸系統主要由推進電機、彈性聯軸器、中間軸承、減振推力軸承、軸段減振器、艉軸、尾前軸承、尾后軸承、螺旋槳等設備組成，其中：軸段減振器為第1 級減振器，減振器剛度為k1，螺旋槳（含附連水）及艉軸、軸段減振器的尾部質量為m1；減振推力軸承為第2 級減振器，減振器剛度為k2，軸段減振器首部、推力軸、中間軸及彈性聯軸器的從動端質量為m2。

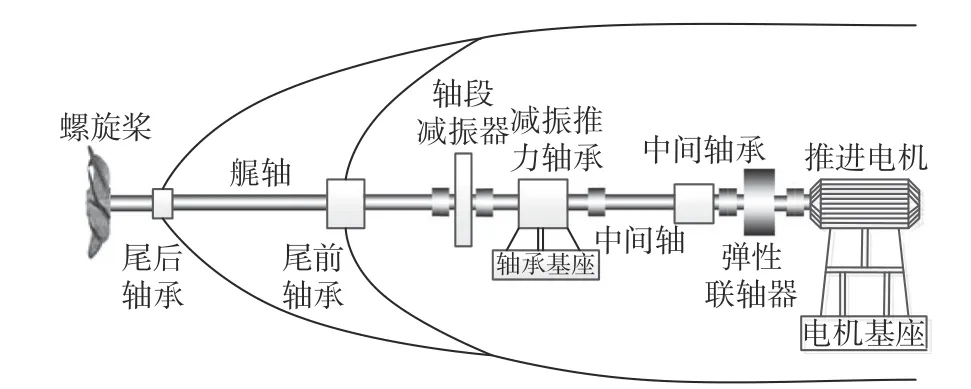
圖10 槳軸系統布置簡圖Fig. 10 Layout diagram of ship propeller-shaft system

該槳軸系統的縱向雙級隔振設計優化方案如下：

1） 在不影響槳軸系統推進功能的前提下，先確定槳軸系統可以實現的最大質量比，取m1=10 t，m2=8 t，μ=0.8。

2） 根據式（8）和式（9），即可得出系統在該質量比作用下的最佳剛度比v=1.8，最低固有頻率比fnmin=2.618。

3） 設定系統一階固有頻率為10 Hz，結合槳軸系統總質量，根據式（3）和剛度比定義，進一步設計減振器的剛度分別為k1=6.9×107N/m,k2=1.24×108N/m。

4） 基于式（5）分析系統的振動傳遞率特性，進一步獲取系統阻尼參數分別為c1=1.2×105N/(m·s)，c2=1×105N/(m·s)。在實船應用中，可以根據隔振器阻尼參數試驗的對比分析結果來獲得合適的振動傳遞率特性。

將應用雙級隔振技術優化之后的槳軸系統與未應用縱向隔振技術、應用單級隔振技術的槳軸系統進行對比分析，獲得其在200 Hz 以內頻段的系統振動傳遞率曲線，如圖11 所示。從圖中可以看出，應用隔振技術之后，一階固有頻率由37.5 Hz下降至10 Hz，系統在15～200 Hz 頻段范圍內均具有隔振能力。在15～35 Hz 低頻段內，由于雙級隔振系統存在二階固有頻率點，故單級隔振系統的振動傳遞率更優，但在35～200 Hz 中高頻段內，雙級隔振系統隔振能力的優勢更為明顯。

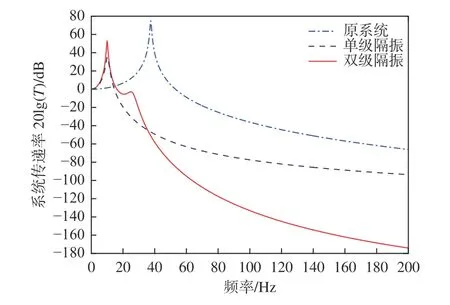
圖11 槳軸縱向隔振系統的振動傳遞特性Fig. 11 Vibration transmissibility of ship shafting longitudinal vibration isolation system

6 結 論

本文提出了基于雙級隔振技術實現槳軸系統縱向振動控制的設計思路，建立了雙級隔振系統的振動數學模型，分析了質量比、剛度比、阻尼比等設計參數對系統振動特性的影響規律，并以某船槳軸系統為例進行了縱向雙級隔振設計優化，得到如下結論：

1） 在給定的質量比或剛度比條件下，應用雙級隔振技術的槳軸系統可以實現最低固有頻率比控制。

2） 系統阻尼比 ξ1的增加對系統二階固有頻率處振動傳遞率的衰減貢獻更為明顯；阻尼比 ξ2對系統一階、二階固有頻率處振動傳遞率的衰減貢獻量基本相當。3） 在15～35 Hz 低頻段內，單級隔振系統的隔振效果較優；在35 Hz 以上的中高頻段內，雙級隔振系統的隔振效果明顯優于單級隔振系統。