高中數學互動教學的策略

鄧圓媛

(江蘇省揚州市大橋高級中學 225211)

在開展數學教學時，教師需要引導學生交互.如果教師沒有優化互動教學的策略，那么學生或者會盲目的交互、或者失去交互的興趣、或者進行低效化的交互.如果要提高互動教學的效率，教師就必須掌握提高互動教學效率的策略.

1 優化情境設計，激發學生找到交互的興趣

教師在引導學生學習數學時，發現很多學生不愿意交互，或者教師點名要求他們交互，他們才交互；或者即使交互了，態度也很被動、消極.如果學生不能理解數學問題是什么意思，發現找不到交互的切入點，那么學生往往提不起交互的興趣.教師如果希望學生積極交互，就要為學生創設良好的學習情境，讓學生覺得自己能理解數學問題，并且能找到交互的切入點.在外部環境的促使、內部環境激發的前提下，學生開始積極交互.

圖1

在學習新知時，教師如果僅僅引導學生從抽象理論角度著手探討新知，學生會找不到交互的切入點，為了讓學生積極探討新知，教師需要為學生創設一個具象化的情境，讓學生從探討具體問題著手來交互理論知識.在選擇問題時，教師要做好新舊知識的銜接，比如讓學生從舊知識入手，把特殊化問題擴展到一般化問題；把新舊知識進行類比，讓學生完成遷移學習等.應用這樣的教學方式，學生能夠與教師交互.

2 組織小組合作，引導學生重視交互的互補

學生存在差異性，他們各有學習優勢和學習不足，教師可以引導學生完成綜合性較強的任務，讓學生在完成任務的過程中分工合作，提高任務完成的效率.在學生完成學習任務以后，為了總結學習經驗，形成系統化的理論，學生需要交互，而在交互的過程中學習能夠形成互補.

以引導學生了解指數函數的圖像與性質為例，教師設計以下的任務：(1)1.72.5與1.73；(2)0.8-0.1與0.8-0.2；(3)a5.1，a5.9；(4)1.70.3與0.93.1.請找到比較以上指數函數大小的方法.學生結合學習經驗，發現如何要找出比較指數函數大小的規律，就必須完成以上案例的學習，然后歸納總結案例，得到問題的答案.學生以分工合作的方法完成以上的任務，在探討任務結合的時候，學生發現小組成員找到了三種解法：用數形結合的方法，這種探討方法比較直觀；用計算器直接計算，它對計算環境和計算設施要求比較高；由函數的單調性考慮，這種方法最簡潔，只是對學生的計算能力要求較高，特別是在探討問題(4)時有些難度,這是因為1.70.3與0.93.1不能直接看成同一個函數的兩個函數值，所以在應用比較單調性時，需要靈活處理數值，比如可以在這兩個數值間找一個中間值(通常是0或1)，這一題選擇這兩數值分別與1比較大小，從而得到答案.學生結合以上的探討總結規律：分析指數函數單調性，可比較指數函數大小：(1)指數函數同底直接用單調性來比；(2)指數函數為變量，則分類探討，再用單調性比；(3)指數函數不同底，比較中間量，比較時應用單調性比.

在探討較為復雜的數學問題時，教師可以引導學生應用合作學習的方式進行交互.教師需要引導學生在交互的過程中分工合作，提高知識學習的效率；通過交互彼此取長補短、相互啟發；在交互的過程中形成理論知識體系.攜手合作，以交互的方式探究知識時，學生會感受到交互的樂趣.

3 應用錯題交互，鼓勵學生拓展知識的學習

學生在學習時，會出現錯誤.如果教師一對一的讓學生寫做錯習題的交互，學生可能會認為教師正在針對他；并且這種一對一的交互，不能讓全班其他學生得到啟示.在教學中，教師可以引導學生觀看經典的錯題案例，讓學生在交互中發現自己的錯誤，然后集思廣議找到錯誤的原因，共同找到正確解決問題的方法.教師可引導學生在交互的過程中延伸學習，拓展學習的范圍，在共同交互中，學生能夠從一道錯題學習中學到更多知識.

教師在開展數學教學時，要為學生預設易錯題，學生在共同學習易錯題時，會發現一道典型的易錯題可能有多種錯解，而這些錯解均反映出學生的一些學習問題.在交互的過程中，錯解會給學生啟示，交互的過程中，學生能通過取長補短，找到正確的學習方向、總結學習經驗.學生們也可以發揮聯想，延伸錯題學習，在共同交互過程中，學到更多知識.

4 交互開放習題，引領學生開拓學習的視野

一般的習題，通常會從已知條件得到唯一的答案，這種習題為封閉式的習題.學生常常學習這樣的習題，會形成封閉化的思路.而有一些習題，或者條件是開放的，或者答案是開放的，或者答案及條件都是開放的.學生探討這類習題的目的，不是為了獲得唯一的解題結果，而是為了在探索習題的過程中，對知識有更加深入的理解；或者能夠形成開放的思路，能夠從多種視角分析問題:

4.1 知識構造類習題

知識構造類習題，是指學生要根據開放式的習題來建構知識，呈現出對知識的理解.學生需要應用習題呈現一個數學知識理論的應用方法、數學計算公式的內容、一種數學思想應用的方法等.在構造習題的過程中，學生會發現自己不只是被動完成習題的人，而是知識的構造者，正因為他們擁有學習的主體性，所以他們更要積極的探索知識及交流知識.

4.2 知識詮釋類習題

知識詮釋類習題，不是為了讓學生得到一個答案，而是為了讓學生結合自己的生活實踐來理解抽象化的數學知識，使學生在個性化詮釋習題的過程中感受學習知識的價值和意義，從而體會到數學概念知識的多樣性，及數學學科知識本身的實用性.不同的學生生活實踐經驗不同，他們詮釋的切入點不同，在交流個性化詮釋結果的過程中，學生會對數學知識有更深入的思考，

以學生詮釋以下的函數為例，教師要求學生結合自己的生活來詮釋函數的圖像.

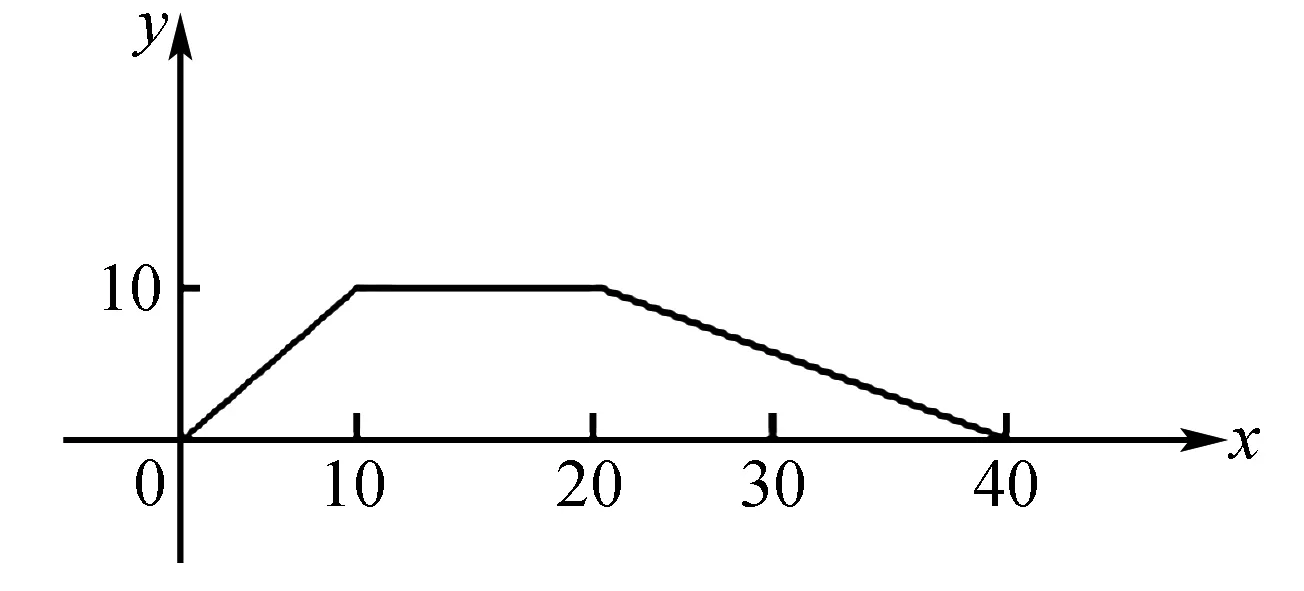
有些學生把函數圖像與生活物品漲價結合起來，有些學生把函數與疫情發生產生的影響聯系起來等.在詮釋的過程中，學生發現一個分段函數能與生活有那么廣泛的聯系，在交流的過程中，學生豐富了自己的生活，感受到了交流的快樂.

開放性習題的設計，能讓學生感受到學習數學知識的結果不是為了得到唯一的解，他們需要去體驗數學知識，感受知識的奧妙之處，感受到學習本身的快樂.而為了讓學生能夠彼此啟發，讓學習開放化性題的完成過程更具趣味性，教師需要引導學生積極的交互，讓學生共同感受學習過程的快樂.

教師在引導學生交互時，一是要明確引導學生交流的目標，教師必須了解通過引導學生交互的同時，能讓學生得到什么樣的學習收獲；教師開展這樣的交互，能避免學生盲目的交互；二是引導學生交流互補、鼓勵學生深入學習及延伸學習；三是要盡可能把交互的平臺交給學生，讓學生多說自己解決問題的思路，然后讓學生在交互中共同激發出思維的火花，找到優化學習的方向.