基于多期搜索蟻群算法的多區型倉庫揀貨路徑優化

胡寒霖 張水旺 陳 康 傅寶潔 汪鵬飛

(安徽工業大學 管理科學與工程學院，安徽 馬鞍山 243032)

0 引言

近年來，我國倉庫的數量、種類和功能快速增長，但是倉庫揀貨效率與發達國家相比，還存在較大差距，這制約了我國物流服務業的快速發展。作為物流服務業的關鍵節點之一，倉庫的揀貨成本和揀貨效率直接影響物流服務的整體效率。因此，對揀貨路徑問題進行優化，提高倉庫揀貨效率，具有較大的現實意義。

學者就路徑優化問題作出了許多研究。方文婷等[1]在路徑優化問題中，加入了節能減排，以總成本最小為研究目標，構造了一種混合蟻群算法，研究了冷鏈物流配送路徑優化問題；馬冰山等[2]結合多配送中心聯合服務模式的特點和純電動物流車輛的行駛特征，針對半開放式多配送中心純電動車路徑優化問題進行深入的研究；任騰等[3]在研究路徑優化問題時，考慮了冷鏈配送客戶滿意度，同時以車輛載重、客戶時間窗和冷鏈產品變質率為約束，構建了以碳排放量最小為優化目標的路徑優化模型，并通過改進型蟻群算法對該問題進行了求解；胡春陽等[4]采用改進的蟻群算法對AGV路徑規劃進行求解；鄭娟毅等[5]將蟻群算法與遺傳算法相結合，提出了一種改進的混合遺傳蟻群算法，解決了不同規模的旅行商問題；任騰等[6]在前述研究的基礎上，同時考慮顧客滿意度和道路擁堵狀況，針對冷鏈車輛路徑優化問題，設計了一種新的知識型蟻群算法。

在路徑優化問題上，除了采用改進的蟻群算法進行求解，還有混合粒子群算法[7]、人工魚群算法[8-9]、遺傳算法[10]、多種遺傳算法[11]、啟發式算法等[12]。基于上述成果，本文針對倉庫揀貨路徑問題進行研究。以揀貨路徑距離最短為目標函數，建立多區型倉庫揀貨路徑優化模型，提出改進的多期搜索蟻群算法，規避蟻群算法容易陷入局部最優而導致算法過早停滯的現象，通過對比傳統蟻群算法、自適應動態搜索蟻群算法和多期搜索蟻群算法求解效率，驗證多期搜索蟻群算法的優越性。

1 問題描述

多區型倉庫由若干相互平行的主通道與巷道組成，貨架平行分布在巷道兩側，集貨點設置在倉庫的左下角。倉庫平面圖如圖1所示，數組{A,R,G}表示相應的儲位編號，其中A為貨物所在區，R為貨物所在行，G為貨物所在列。例如{2，3，5}表示貨物位于2區、3行、5列。

2 模型構建

2.1 基本假設

(1) 每個儲位只儲存一種商品。

(2) 揀貨車存在容量限制，且揀貨車容量均相等。

圖1 多區型倉庫平面示意圖

(3) 每個儲位上的揀選商品需一次揀選完畢，不得拆分為多次揀選。

2.2 參數設置

H：點的集合；

I：邊的集合；

D：距離矩陣；

N：揀貨點編號集合，N=(H,I,D)；

vi：第i個儲位，其中v1為集貨點，v(n+1)為最后一個揀貨點；

dvivj：儲位vi到儲位vj的最短折線距離；

Q'：揀貨小車額定載重量；

m：子路徑總數(揀貨車數量)；

k：子路徑編號；

2.3 數學模型

假設揀貨員從v1開始揀貨，當到達vn時小車載重量超過Q'，則在序列的n個元素前增加一個起點，并從第n個元素開始重新計算載重，最終形成一個由若干條路徑組合而成，且滿足小車載重的約束。基于此，以揀貨路徑距離最短為目標[13]，構建數學模型如下：

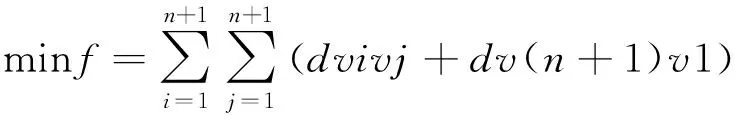
(1)

s.t.

(2)

(3)

(4)

(5)

xvivj∈{0,1}

(6)

其中，k=1,2,…m，i,j=1,2,…n+1。

式(1)表示目標函數，為求解總路程最短路徑；式(2)表示貨物裝載量之和需小于揀貨車額定載重量；式(3)、式(4)表示每個點有且僅有一次通過機會；式(5)表示不存在最小回路；式(6)表示決策變量xvivj可能的取值，當xvivj為1時，表示揀貨過程中經過了i和j兩個點，當xvivj為0時，表示揀貨過程中未經過i和j兩個點。

3 改進蟻群算法

3.1 基本蟻群算法

蟻群系統是由Dorigo、Maniezzo等[14]于20世紀90年代首先提出來的。自然界中蟻群可以克服地勢及距離的重重阻礙，在洞穴與食物之間找到一條最佳路徑，究其根本是因為蟻群中存在一套以“信息素”為核心的反饋機制，這種機制能夠合理挖掘潛在路徑并充分利用，最終找到一條較佳路徑，蟻群算法應運而生。它在TSP問題上具有良好的適應性，同時也適用于TSP問題衍生出的多回路問題，即VRP問題。

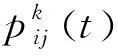
(7)

τij(t+n)=(1-ρ)τij(t)+△τij(t)

(8)

(9)

(10)

3.2 算法改進

基本蟻群算法針對VRP問題具有良好的適應性，但其仍具有一定的局限性，主要表現在當問題規模較大時，算法容易陷入局部最優化從而導致算法過早的停滯。文獻提出一種動態自適應搜索蟻群算法[15]，能有效解決早熟問題，但仍有優化空間。本文基于原有算法提出多期搜索蟻群算法模型，用以引導算法探索最優路徑和提高算法的收斂性能。

3.2.1 分段式信息素強度

單獨標志的序號放在引文責任人之后，且設置其格式為上標，闡述中出現的引文序號不需要上標，正文中的引用文獻若需指明文獻責任人，則僅需寫出第一責任人，外文文獻僅需寫出其姓氏即可。

由蟻群算法的特性可知，當出現一只螞蟻在一條路徑上覓食很久時，放置一個更近的食物基本沒有效果，其原因可以理解為當初一只螞蟻留下了較為濃烈的信息素，此后一段時間大量螞蟻均選擇了這條路線，該路線上的信息素濃度不斷升高。這時即使有一只螞蟻找到更近的路徑，由于時間間隔過久，兩條路徑上的信息素濃度相差較大，整個系統基本已經停滯了，陷入局部最優。因此，本文中采用式(11)的分段函數Qi來替代式(10)中的固定常數Q：

(11)

當函數最優值處于一段時間沒有持續變化時，說明搜索可能陷入了局部最優。故將蟻群算法的完整迭代過程分為若干個“搜索期”，其中Ti為第i個搜索期的結束時間。在進入新的搜索期后改變信息素常量，使得信息素濃度處在較高水平時，新發現的較優路徑仍能給蟻群提供較好的指導性，從而避免陷入局部誤區。

3.2.2 信息素導向與啟發信息的權重比例

本文針對原有的信息素導向與啟發信息之間的固定權重提出以下改進方法：

當t≤T1時，信息素導向和啟發信息權重分別為：

(12)

當t>T1時，信息素導向和啟發信息權重分別為：

(13)

在同一搜索期內，隨著迭代次數的增加，信息素權重μ與啟發信息權重η的比重不斷變化。當蟻群完成一段搜索期后，信息素權重會產生一個負向的“跳變”，啟發信息權重會產生一個正向的“跳變”，其中k1和k2為信息素調整數與啟發信息調整系數，決定著“跳變”的大小和新一輪搜索期內μ與η的比例。在Q、μ與η的共同作用下，同一搜索期前期算法側重于對新路徑的隨機選擇，而在后期更側重于對較好路徑的深度挖掘，從而完成參數的自適應。

3.2.3 轉移概率

針對轉移概率，本文進行如式(14)所示的轉移規則，進行改進。

(14)

4 算例分析

4.1 算例求解

對淘寶某電商倉調研得到的數據進行整理，求解貨架與貨架間的最短路徑。設置初始參數，將模型與相應數據相結合，迭代150次后，得到最終路徑規劃方案如圖2所示。

圖2 揀貨路徑示意圖

基于本文算法求得，路線總長為832米，最佳的揀貨路徑為：

揀貨路徑1：(0,6,14,12,4,5,15,20,9,0)；

揀貨路徑2：(0,1,8,13,18,10,2,17,3,0)；

揀貨路徑3：(0,11,16,19,7,0)。

該倉庫目前采用的是“U+返回”型揀貨策略，同樣的數據，“U+返回”型揀貨策略的揀貨路線總長為937.6米。因此，本文方法可以提升該倉12.7%的作業效率，說明本文方法能有效節約揀貨路徑。

4.2 結果分析

為驗證算法改進前后的優越性，本文隨機生成一組40貨位的訂單，揀貨點信息如表1所示，采用傳統蟻群算法(ACO)、自適應動態搜索蟻群算法(ADACO)和多期搜索蟻群算法(MSACO)分別求解10次，結果如表2所示。

表1 揀貨點信息

表2 不同算法運行結果匯總

從表2可以看出，ACO算法的配送成本的最佳值僅有965.2，且收斂代數與運行時間有著較大的起伏，算法不具備穩定性；ADACO算法的揀貨成本集中于930附近，但其收斂代數較高，運行時間較長；MSACO在保證揀貨成本較低的前提下，迭代次數較ADACO節約了14.93%，其求解結果處于910～940之間，具有良好的穩定性。

圖3顯示出3種算法的收斂曲線，由曲線可以看出傳統ACO算法較早陷入局部最優并停滯；ADACO具有良好的跳出局部最優的能力，但在迭代后期挖掘潛能欠佳；MSACO算法對新的路徑具有較好的挖掘能力，能有效解決蟻群算法的“早熟”問題。

圖3 最小成本變化趨勢對比

5 結語

本文針對多區型倉庫揀貨路徑優化問題構建了數學模型，提出改進的多期搜索蟻群算法，經仿真實驗對比結果可以看出，改進的多期搜索蟻群算法在揀貨路徑優化問題上具有一定的優越性。后續將基于算法去探索其他路徑優化問題，尤其一些更為復雜的路徑優化問題。