一道研究生入學考試題的思考

高巧琴

(呂梁學院 數學系， 山西 離石 033001)

0 引言

數學分析的研究對象是函數，主要研究函數的三大分析性質：連續性、可微性與可積性，而極限是研究它們的主要工具，是貫穿數學分析的一條主線.因此,掌握好極限的求解方法是學習數學分析的關鍵環節.極限包含數列極限與函數極限，二者是特殊與一般關系，要掌握求極限的方法，首先從最基本的數列極限開始.

求數列極限的方法繁多，學生碰到這類問題時常常會出現對方法選擇的困惑.以南京師范大學2017年研究生入學考試數學分析第一題的一道數列極限為例，分析探討學生易出現的誤區及合理選擇正確方法求解數列極限.

試題計算極限：

筆者針對這道題目的解法分析，探討在教學中如何打破學生的定勢思維和培養學生的創新思維能力.

1 解法分析

很多同學首先想到利用迫斂性求解：

因為

(1)

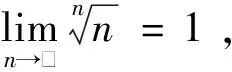
這樣的解法是錯誤的，錯在哪里呢？

可以看出，對于所有的n并不是單調的，而是從第三項開始是嚴格單調遞減的，如圖1所示.

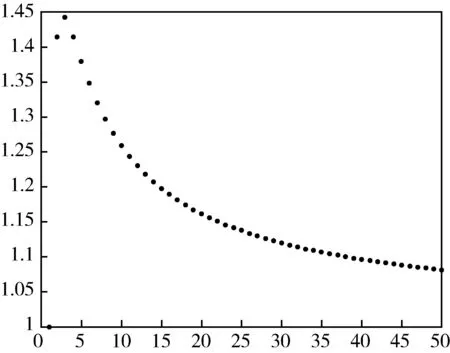
圖1 數列的圖像

結構分析這屬于數列極限問題，從形式上看，是關于n項和的極限，但不能直接應用數列極限的四則運算法則，因為隨著n的增大數列項數不斷增加，而四則運算法則只適用于有限個數列的和，鑒于此，常規的思路是先求和再求極限.

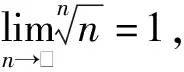
方法1：(利用均值極限)

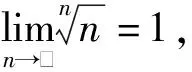
方法2：(利用施篤茲定理)

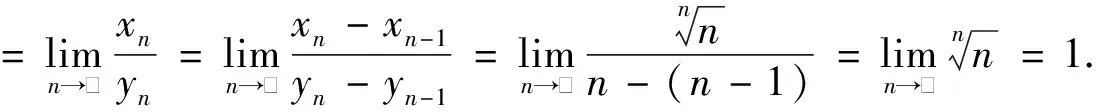
2 幾點反思

2.1 教師在教學過程中，一方面要注重基本概念的解析、基本理論的拓展、基本方法的使用、典型錯誤的剖析；另一方面，要打破學生的思維定勢，全方位考慮問題，可以培養學生的探索精神，提高學生解決問題的能力和創新思維能力[3].

2.2 學生在學習過程中，要研究各種解題方法的原理本質，總結在解題過程中容易出現的誤區，注意知識的嚴謹性，學會全面分析解決問題的能力.