利用思維可視化提升初中生數學學習效率

陳珠

【摘要】在初中數學教學中圍繞創設情境、梳理知識、簡化難點、發展思維、解決問題等環節，合理利用思維可視化，能有效地激發學生探究數學的積極性、創造性和提高學生知識建構能力、知識遷移能力。

【關鍵詞】思維可視化;初中生;數學學習

思維的可視化，簡言之就是將思考方法和思考路徑通過圖形或者是統計表格等各種形式進行顯現，從而使其更加直觀化和具象化。初中數學教師進行教學時，如果有效利用這種方法，就能夠幫助學生有效地梳理數學學習過程，降低數學的學習難度，引導學生數學思維有序發展，不斷提升其數學學習力。

一、創設問題情境，進行問題可視化導入

問題是數學思維的重要支點，問題導入在數學教學中能有效啟發學生思維，在學生的認知當中形成矛盾點，引發其進行思考，從而主動投入到數學探究當中。同時，問題導入還需要關注學生實際情況，以其已經具備的知識經驗作為立足點，融合教學內容，為學生創設有利于其思維發展的問題情境，使學生認識到教學材料也是非常有趣的，并愿意投入思考，主動學習。

例如進行九年級上冊的“圖形的旋轉”教學，教師可以借助多媒體的圖片展示功能，向學生展示風扇、對稱的窗花、秋千、時鐘、推拉窗、電梯等各種圖片，然后構建思維導圖，以“圖形變換”為中心，以“軸對稱”“平移”“旋轉”為枝干，并提問：“你能根據圖形變換特點將其拖動到對應的思維導圖枝干中嗎？”教師通過圖形呈現和思維導圖，不僅能使學生對圖形旋轉特征有基本的認知，而且能使學生將新知識與之前學過的軸對稱等知識有機聯系。設問引思，促進學生的思維發散，引導學生回顧舊知識，并對新知識產生學習欲望。

二、根據知識層級，建立遞進式知識體系

初中數學中很多知識點是以遞進式層級關系聯系在一起的，針對這一類型的知識體系，教師可以將基礎知識點提取出來，由淺入深，層層遞進，用圖示呈現出來，使學生通過圖示直觀清晰地認識到知識點的層級關系。

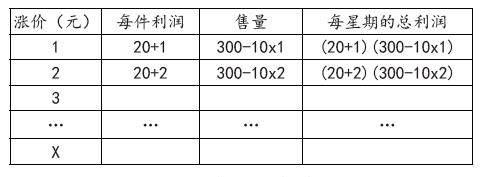
例如，在九年級上冊“實際問題與二次函數”的教學中，教師可利用思維可視化方法，將二次函數的最大值問題融入到實際生活中：一個玩具店新進毛絨玩具，進價是40元，將其標價為60元后，每周可以出售的數量是300件。通過市場調查，如果商家將標價上調，那么每上調1元，每周出售數量就會少10件，問：如何定價才能使每星期的利潤最大化？

分析：這個問題如果直接讓學生引進兩個變量，然后寫出函數關系式，多數學生會感覺抽象，這不利于解決該問題。教師設置成下面的思維可視圖，或許能讓大多數學生很快地寫出函數關系式（寫出函數關系式是本問題的關鍵）。

把表格中空白部分的內容填滿。

設每星期的總利潤用y（元）表示，則y與x之間的函數關系式為y=（20+x）（300-10x）。

三、聚焦易錯點，加強對易混淆知識點的把握

初中生在數學學習中，有時候會出現“聽得懂卻不會做”的尷尬情形。這主要是因為學生對知識點的把握不到位，尤其對很多易混淆的知識點，在運用中出現無從下手的情況。針對此問題，教師可利用思維導圖來對比易錯知識點，直觀呈現知識點的差異，引導學生正確理解、準確把握知識點。

例如，在學習無理數后很多學生會錯誤地認為帶根號的數就是無理數，將等有理數也當成是無理數。針對這種情況，教師在教學中可利用思維導圖，引導學生將無理數和有理數的異同點進行歸納總結，并分析誤解原因，從而加強學生對知識點的理解與把握。

該教學內容的思維導圖為：

通過這個思維導圖，加強學生對有理數與無理數這兩個不同概念的理解及掌握。

四、建立解題模型引導學生舉一反三解決難題

在解答數學問題時，解題模型的構建過程就是思維運動的過程。教師在解題教學中引導學生建立解題模型，可以使問題更加具體化和直觀化。通過流程圖，形成數學題目解析的暢通流程，凸顯解決問題的思維路徑及方法，使學生掌握這種方法，舉一反三，觸類旁通。

例如，幾何問題是初中階段數學學習的一個重要知識點，在解答幾何問題時怎樣利用好輔助線并熟練運用輔助線是解決幾何問題的關鍵。基于此，教師可指導學生建立輔助線解題模型，先判斷問題類型，如倍角問題、中點問題、垂線段問題等，然后判斷輔助線類型，并最終解決問題。教師運用解題模型，加強學生的理解與記憶，使學生通過掌握模型實現舉一反三，解決同類問題。

例題：已知ΔABC中，AB=5，AC=3，連BC上的中線AD=2，求BC的長。可以作出倍長中線得到全等三角形求解（如圖1）。

本題選擇倍長→創造全等：延長AD至點E，使DE=AD，連接BE易證△ADC≌△EDB，從而有DE=AD=2，BE=AC=3，CD=BD，所以AE=4。在△ABE中，有32+42=52即BE2+AE2=AB2，由勾股定理的逆定理得△ABE為Rt△且∠AEB=90°。在Rt△BDE中由勾股定理，得BD= ==，所以BC=2BD=2，即BC的長為2。

五、利用錯題資源，拓寬學生的思維廣度

解題過程中難免會出現錯題，錯題是非常寶貴的學習資源，它暴露出個體在學習中的薄弱環節和思維缺陷。在數學解題教學中教師要重視錯題資源，利用思維可視化，指導學生根據自身實際情況對錯題進行梳理歸納，繪制錯題思維導圖，將錯誤原因、例題和正確解題方法均呈現在思維導圖中。每個學生都可根據自己的易錯題類型繪制思維導圖，把對易錯題的分析直觀地呈現出來。這不僅有利于學生掌握知識，提高解題能力，而且對于拓寬學生思維廣度，促進其創造力發展也具有重要意義。

下面以解一元一次方程為例：

解一元一次方程

該方程的正確解法：

-=1，

去分母，得3（x-4）-2（2x+1）=6;

去括號，得3x-12-4x-2=6;

移項，得3x-4x=12+2+6;

合并同類項，得-x=20;

系數化為1，得x=-20。

總而言之，思維可視化在引導學生思維發展方面具有非常明顯的作用，有利于學生掌握數學學習方法，提高數學能力。

【參考文獻】

[1]王金鳳.初中數學思維可視化課堂的實踐研究[J].求學，2021（31）.

[2]高育香.思維可視化在初中數學教學中的應用探討[J].新課程，2021（21）.

[3]謝海燕.思維可視化在初中數學教學中的應用探究[J].陜西教育（教學版），2020（3）.