融合信息技術的“行星的運動”物理教學

郭雪鵬

20世紀90年代以來，信息技術與課程整合一直是重要的研究課題，信息化、現代化是教育改革的主旋律。然而，教育教學質量并沒有得到令人滿意的提升。由此引發著名的喬布斯之問——“為什么計算機改變了幾乎所有領域，卻唯獨對學校教育的影響小得令人吃驚？”^[1]究其原因，一是有些教師甚至教育技術專家對信息技術與學科教學深度融合缺乏正確認知;二是有些教師教育觀念陳舊，將信息技術視為輔助教學可有可無的工具，認為沒有信息技術，教學依然能進行;三是部分教師不了解為什么要進行信息技術與學科教學深度融合，什么是深度融合，如何將信息技術與學科教學深度融合。

一、正確理解信息技術與學科教學深度融合的內涵

信息技術不是可有可無的課堂教學輔助工具，將信息技術融合于學科教學是教育發展和改革的時代要求。教育信息化、現代化是大勢所趨。信息技術與學科教學深度融合旨在促進自主、合作與探究等新模式教學，改變長久以來的“滿堂灌”教學模式。傳統模式下，教師是中心，教師在短時間內向學生單向傳授大量知識，效果并不理想：學生的學習主動性喪失，學生的批判性思維和科學思維能力沒有得到有效提升。傳統模式下培養的學生往往習慣性將教師和專家及教材視為權威，不敢提出反對意見，對問題缺乏獨立見解，不敢表達也不會論證自己的觀點。信息技術與學科教學深度融合就是要改變這種以教師為中心的課堂教學結構，建立一種同時發揮教師主導作用和體現學生學習主體地位的“主導—主體相結合”的教學結構^[2]。信息技術在學科教學深度融合為自主、合作、探究活動的開展創造了信息化的教學環境。教師應利用信息技術創建教學情境，讓學生便捷獲取信息和資源進行自主探究和協作學習，發揮其主動性、積極性，最終實現變革傳統課堂教學結構的目標^[3]。信息技術與學科教學是否實現了深度融合，關鍵要看以教師講授為中心的傳統教學結構是否改變，并被“教師主導—學生主體相結合”的新教學結構代替。

信息技術與學科教學深度融合需要大量、類型豐富的數字化教學資源作支撐，助力教師主導作用的發揮和學生自主探究與協作學習。教師既可以從互聯網上獲取各種資源，也可以自行開發或制作教學資源。以物理學科為例，常用的教學軟件有幾何畫板、仿真物理實驗室、Adobe Flash、Algodoo和MATLAB等。網絡空間上的資源非常豐富且容易獲取，教師應有選擇地收集、分類，并將其融入物理課堂教學。同時，教師也要熟練掌握常用軟件，具備開發數字化教學資源的能力，不斷提高數字化教學能力。

二、應用幾何畫板探究八大行星的運動規律

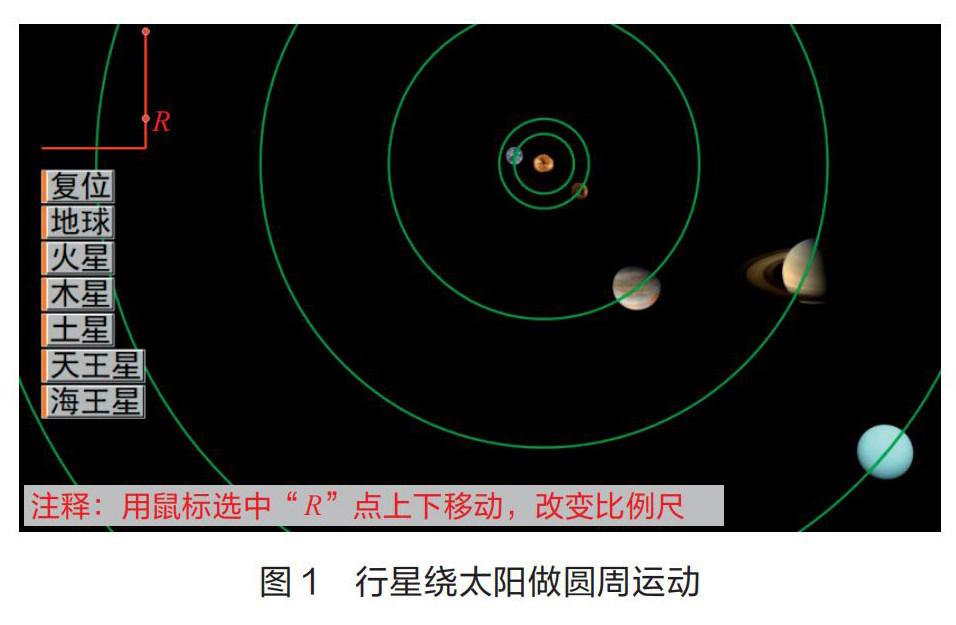
幾何畫板最初是一款數學軟件，現在眾多物理教師也將其應用于物理教學^[4]。筆者將結合課例，探討信息技術與高中物理課堂教學深度融合的路徑。八大行星繞太陽近似做勻速圓周運動，行星軌道半徑r越大，角速度ω、線速度v、加速度a越小，周期T越大。高一學生初次學習這部分內容時，難以掌握行星圓周運動的這些物理量與半徑的關系，不少學生無法利用萬有引力定律進行數學推理得到結論。高一學生普遍抽象思維能力和邏輯推理能力不強，解決問題多靠形象思維。如果學生頭腦中沒有建立生動形象的圖景，思維就存在障礙，不能調用已有的知識解決問題。為此，筆者查閱行星軌道半徑參數，依據萬有引力定律計算得到各行星圓周運動的線速度比值，利用幾何畫板軟件模擬行星的公轉運動（如圖1），引導學生觀察、思考。

人們可以依據各行星到太陽距離的實際數據，計算行星到太陽距離與地球到太陽距離的比值，按照比例確定各行星的軌跡半徑。如果操作者用鼠標選中并移動課件中“R”點可以改變地球到太陽距離，各行星到太陽的距離將同步改變。筆者用網絡上找到的高清圖片表示各行星，生動逼真，能吸引學生的注意力，激發學生探究的好奇心，體現多媒體教學資源開發的藝術性。用戶單擊圖中按鈕，行星即繞太陽運動，再次單擊，運動停止。這樣的課件具有交互功能，便于學生自主操作和探究。建構主義學習理論認為新知識的學習應與學習者已學的知識相互聯系，教師應在學生原有知識基礎上加以擴充、深化、改造，完成學習者知識結構的更新。依據建構主義理論，筆者設計了如下教學過程。（以下為主要片段）

教師：請大家觀察各行星運動快慢，思考線速度和半徑有何關系。（教師演示課件）

學生1：行星軌道半徑越大，運動得越慢。

教師：“運動得越慢”是指哪個物理量？

學生1：線速度。軌道半徑越大，線速度v越小。

教師：軌道半徑r越大，周期T如何變化？

學生2：周期T越長。（學生通過課件演示直接觀察得到結論）

教師：能從理論上解釋為何半徑越大周期越長嗎？

（學生2無法遷移所學知識解決問題）

教師：行星的軌道半徑r和周期T有何定量關系？前面哪一節學習過？

學生（全體）：r³/T²是一個定值。

教師：根據開普勒行星運動的第三定律可知，行星軌道半徑越大運動周期越長。

教師：角速度ω與半徑有何關系？如何分析？

（停留20秒，留給學生時間思考）

學生3：半徑r越大，角速度越小。因為半徑r大，根據開普勒第三定律可得其周期T越大。根據ω=??????可知，周期越長，角速度越小。

教師：分析得很不錯！推理很嚴謹。如何理解軌道半徑r越大線速度v越小？根據v=ωr可以判斷出結果嗎？

學生4：無法判斷。r越大，角速度ω越小，無法判斷二者乘積與r的關系。

教師：能定量求解線速度與半徑的關系嗎？行星做勻速圓周運動，向心力由什么力提供？向心力與線速度、軌道半徑有何關系？

學生：太陽對行星的萬有引力提供向心力，向心力F_n=m。

教師：請根據萬有引力提供向心力，求解線速度的表達式，并分析線速度和行星軌道半徑的關系，推導加速度、角速度和周期與軌道半徑的定量關系。

筆者用幾何畫板創設模擬情境引入生動逼真的教學內容，引發學生的好奇心。借助技術工具，筆者模擬行星的運動，引導學生得到行星線速度、周期和軌道半徑的關系。筆者通過啟發式教學，通過問題鏈對學生進行啟發、提示，引導學生推理分析，使其觀察結果建立在嚴密的邏輯推理上，新內容的學習建立在所學知識基礎上，進而發展其科學思維和數理推理能力。

三、信息技術輔助探究行星沖日問題

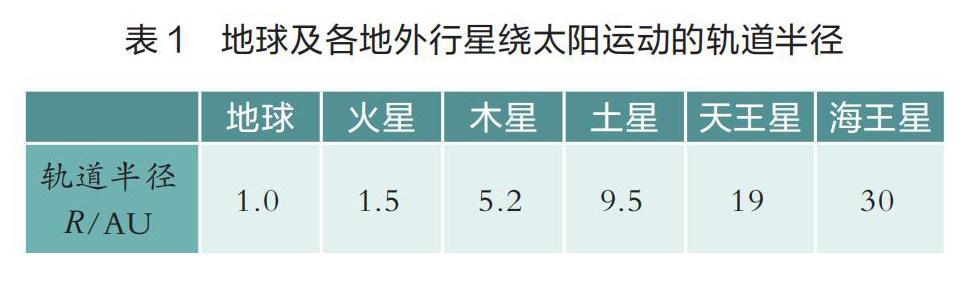
人教版《物理》必修第2冊72頁第6題：太陽系各行星幾乎在同一平面內沿同一方向繞太陽做圓周運動。當地球恰好運行到某地外行星和太陽之間，且三者幾乎排成一條直線的現象，天文學稱為“行星沖日”。已知地球及各地外行星繞太陽運動的軌道半徑（見表1），根據題中信息，試計算木星相鄰兩次沖日的時間間隔，哪顆地外行星相鄰兩次沖日的時間間隔最短？

審題是解決問題的第一步，學生通過讀題、分析題目條件，理解題目情境，建構物理模型。對于純文本題型，學生審題后應能用示意圖重構題目情境，在示意圖上標出關鍵狀態、物理量、受力、速度、加速度等信息。不少學生不會解題，原因之一是沒有讀懂題目，不能用圖畫表征題目情境，頭腦中沒有建立情境畫面，不能建立動態的情境畫面，難以模擬物體的運動情境動畫。對于此題，學生解題的困難之一是想象行星的運動圖景，在頭腦中想象各行星的運動及位置關系。

為引導學生解題，筆者在信息技術支持下開展了如下教學。

教師：請畫出第一次木星沖日時，木星、地球和太陽的位置關系。

絕大多數學生能畫出木星沖日時三者位置關系。

教師：第一次木星沖日，木星和地球繞太陽做圓周運動，哪顆行星轉動得快，哪顆行星轉動得慢？請想象不同行星繞太陽運動的動態畫面。

很多學生顯露茫然的表情，不能判斷木星和地球轉動快慢，無法建立木星和地球繞太陽轉動的動態情境。教師打開制作的幾何畫板課件，模擬木星沖日。學生觀看課件，尋找運動規律。

教師 ：木星和地球繞太陽做勻速圓周運動的角速度相等嗎？為什么？

學生：木星的角速度小于地球的角速度。木星軌道半徑大，根據開普勒第三定律可知，木星繞日運動的周期大，運動角速度較小。

教師：第二次木星沖日，地球和木星轉過的圓心角相等嗎？有何關系？

學生1：地球轉過的圓心角大。

教師：地球和木星轉過的圓心角有何定量關系？

學生1無法解答該問題。教師再次演示模擬動畫（如圖2）。再次觀看后，不少學生觀察出地球轉過的圓心角與木星轉過的圓心角之差為2π，但仍有部分學生無法理解該定量關系。教師安排如下學生分組做模擬實驗。

分組實驗：學生兩人一組，用紙揉成兩個大小不同的紙球，分別代表木星和地球;在白紙上畫半徑不同的兩個同心圓，圓心表示太陽，大圓、小圓分別表示木星和地球繞太陽運動的軌道。學生A手持“木星”，學生B手持“地球”。初始時，“木星”“地球”和“太陽”三者共線，且“木星”和“地球”位于“太陽”的同側。學生B手持“地球”繞“太陽”運動較快，學生A手持“木星”繞“太陽”運動較慢，當“木星”與“地球”再次位于“太陽”同側且三者共線時，停止運動。

學生分組實驗后，教師請兩名學生在黑板上模擬木星和地球的運動，演示木星沖日現象，在黑板上記錄下兩次沖日時地球和木星的位置關系。

設計意圖：教師組織學生分組實驗，培養學生協作學習意識和合作學習能力。兩名學生只有多次磨合，彼此協作才能取得較好的演示效果。學生在模擬活動實驗過程可體會、感悟行星運動快慢，總結兩次沖日間隔地球和木星轉過的圓心角關系。

教師：通過實驗，兩次木星沖日間隔，大家發現地球和木星轉過的圓心角有何關系？

學生2：ω_地t-ω_木t=2π。

教師：題目中沒有說明地球和木星的角速度，地球公轉周期T_地=1年作為已知量。如何表示上述關系？

學生2：t=2π。根據開普勒第三定律有?????????????????，解出木星公轉周期。

教師：請按照上述思路推導木星沖日的時間間隔表達式。

學生推理得到木星沖日時間間隔表達式，并根據表達式分析發現，行星運動周期越大，兩次沖日時間間隔越短，海王星的軌道半徑大，周期最大，海王星兩次沖日的時間間隔最短。

教師：能提出一個新問題并進行解答嗎？

（學生沉默不語，無法提出新的問題。）

教師：兩次木星沖日時，木星距離地球最近。（教師加強“最近”兩個字的語氣）能提出一個類似問題嗎？

學生：可以詢問第一次木星沖日到下一次木星和地球距離最遠時經過的時間間隔。

教師：這是一個不錯的問題。請大家畫圖分析，下一次木星和地球距離最遠時兩行星轉過的圓心角的關系。

學生：地球比木星轉過的圓心角多1個π。

部分學生很快看出結果，教師保持沉默，繼續讓學生畫圖分析，留給學生時間思索、解決問題。教師使用幾何畫板（課件）演示從第一次木星沖日到下一次木星和地球距離最遠的模擬動畫，引導學生觀看動畫演示，探究木星和地球轉過的圓心角關系。學生通過動畫知曉，地球和木星距離最遠時，二者轉過的圓心角相差π，根據圓心角關系求解時間。2分鐘后，教師請2名學生將寫在紙上的求解過程和結果上交，用交互式電子白板的投屏功能進行投影，分析作答情況。

教師借助幾何畫板進行動畫模擬解決了教學中的難點問題。很多工具既支持教師課堂講授演示使用，又支持學生在課內外自主探究。仿真實驗技術為學生提供自主探究的技術支撐，促進了教與學方式的改進。此課例的教學既體現了教師的課堂引導作用，又彰顯了學生的學習主體性，學生在學習中不僅聆聽教師講解，還在教師提示下積極思索，解決問題。

21世紀，教師要培養的是具有創造能力的創新型人才，而信息技術與學科教學深度融合是實現教育教學目標的重要途徑。信息技術與學科教學深度融合是提高教師教育教學能力、促進教師專業發展的重要時代機遇。教師是教育改革的踐行者，應積極投身于新一輪課程改革，積極探索信息技術與各學科教學深度融合的教學方法和路徑，探索有效支持“主導—主體相結合”教學結構的帶有教師個人烙印的新型教學方法。

注：本文系安徽省阜陽市2021年教育科學規劃課題“信息技術與高中物理教學深度融合的資源開發、路徑與教學的實踐研究”（課題批準號：FJK21032）的研究成果。

參考文獻

[1] 王慶環.“喬布斯之問”問出什么教育問題？[N].光明日報，2015-12-08（14）.

[2] 何克抗.信息技術與學科教學“深度融合”的路徑與實現方法[J].中小學數字化教學，2018（2）：17-20.

[3] 何克抗.如何實現信息技術與學科教學的“深度融合”[J].教育研究，2017，38（10）：88-92.

[4] 韓建光.物理深度學習與數字化教學融合的探索與實踐[J].中小學數字化教學，2017（3）：8-11.

（作者系安徽省臨泉第一中學物理教師）

責任編輯：祝元志