用數學思想引導生成課堂及簡評
王紅華


筆者曾受邀參加咸寧市名師工作室研討活動,會上研討了一節“一題一課”型的復習課.大部分教師在討論中提出,中考前的數學復習課難上,認為復習課是“三無”產品,即“無教材、無教參、無教案”,因此許多教師往往依賴各類教輔資料搞“題海戰術”,導致學生學習負擔加重,阻礙數學素養的提升.而“一題一課”的課型就是讓學生走出題海,減負增效.這種課型以一個問題為背景材料,深度挖掘問題的條件、結論和解決問題的思路,引導學生多角度思考,從知識體系的高度去變式拓展,探究新的問題解決方案,并提煉其中所蘊含的數學思想方法,揭示問題的本質,促進思維能力的發展,進而提升學生的關鍵能力和學科素養.
筆者以人教版八年級上冊第十三章第4節的課題學習“最短路徑問題”的問題1為素材,討論用數學思想引導基于“一題一課”型復習課的生成過程并作簡要評析.
1 課本問題呈現
問題 如圖1,牧馬人從A地出發,到一條筆直的河邊l飲馬,然后到B 地.牧馬人到河邊的什么地方飲馬,可使所走的路徑最短?
2 課堂生成思路
此問題也叫將軍飲馬問題,是每年各地中考的熱點之一.解決本問題可以作出點A關于直線l的對稱點A′,如圖2,連接A′B,交直線l于點C,即AC+BC最小.本問題通過軸對稱變換,將直線同側兩點中的一個點變換到另一側,而不改變路徑的總長度,利用“兩點之間線段最短”解決本問題.這其中蘊含化歸思想,在解決問題的過程中軸對稱變換起到了橋梁作用.
此問題為解決最短徑問題提供了思考方法,下面繼續對本問題進行思考.此問題中對象的特征是:有三個點,其中一個點在直線上,另兩個點實際上是兩定點且在直線的同側.用運動變化的觀點,從特殊到一般的思想去思考,能否由定點想到動點,而動點往往在某個幾何圖形上,由此我們可以聯想到點A,B在某個幾何圖形上,由靜到動多角度變式拓展,聯系前后所學數學知識,將此問題逐步推進,提出新問題,然后分析問題,解決問題,進而加深對知識的理解,提高綜合運用知識解決問題的能力,同時提升思維的廣闊性和深刻性.
2.1 聯系直線型生成
上述已經聯想到點A,B在某個幾何圖形上,可以用分類的思想,將初中幾何圖形簡單分為直線型、圓、一般曲線型(拋物線、雙曲線).最簡單的一種,如問題1:如圖3,直線l1與直線l2相交于點O,點B為一定點,若點A在直線l1上且與點B在直線l2的同側,點C為直線l2上一點,當點A與點C分別在何處時,AC+BC的值最小?
解法指引:
問題1與將軍飲馬問題不同之處在于點A不是定點,但A和B都在直線l2的同側,這與將軍飲馬問題中的對象有相似性,可以將此問題歸類為將軍飲馬問題,進而類比將軍飲馬問題的解決方法去求解.學生容易想到用以下思路一解決.
思路一:如圖4,作點B關于直線l2的對稱點B′,此時BC=B′C,求AC+BC的最小值,問題轉化為點到直線的距離.過點B′作直線l1的垂線,垂足為點A,連接AB′交直線l2于點C,即點A,C為所求點.
用整體的思想繼續思考,若將直線l1看作是“定”的整體,能否通過類比將軍飲馬問題加以解決?于是指導學生用以下思路二加以解決.
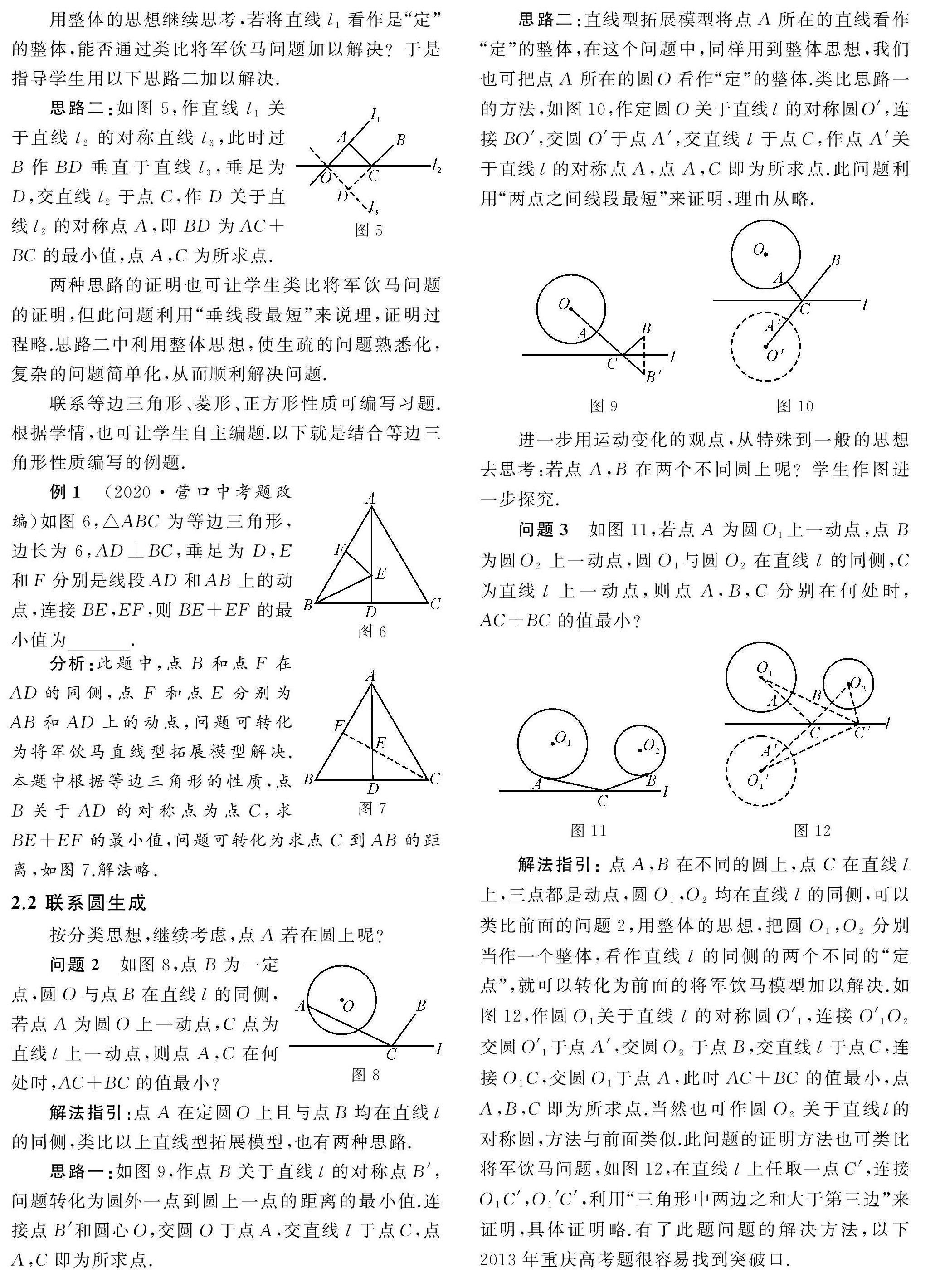
思路二:如圖5,作直線l1關于直線l2的對稱直線l3,此時過B作BD垂直于直線l3,垂足為D,交直線l2于點C,作D關于直線l2的對稱點A,即BD為AC+BC的最小值,點A,C為所求點.
兩種思路的證明也可讓學生類比將軍飲馬問題的證明,但此問題利用“垂線段最短”來說理,證明過程略.思路二中利用整體思想,使生疏的問題熟悉化,復雜的問題簡單化,從而順利解決問題.
聯系等邊三角形、菱形、正方形性質可編寫習題.根據學情,也可讓學生自主編題.以下就是結合等邊三角形性質編寫的例題.
例1 (2020\5營口中考題改編)如圖6,△ABC為等邊三角形,邊長為6,AD⊥BC,垂足為D,E和F分別是線段AD和AB上的動點,連接BE,EF,則BE+EF的最小值為? ??.
分析:
此題中,點B和點F在AD的同側,點F和點E分別為AB和AD上的動點,問題可轉化為將軍飲馬直線型拓展模型解決.本題中根據等邊三角形的性質,點B關于AD的對稱點為點C,求BE+EF的最小值,問題可轉化為求點C到AB的距離,如圖7.解法略.
2.2 聯系圓生成
按分類思想,繼續考慮,點A若在圓上呢?
問題2 如圖8,點B為一定點,圓O與點B在直線l的同側,若點A為圓O上一動點,C點為直線l上一動點,則點A,C在何處時,AC+BC的值最小?
解法指引:
點A在定圓O上且與點B均在直線l的同側,類比以上直線型拓展模型,也有兩種思路.
思路一:如圖9,作點B關于直線l的對稱點B′,問題轉化為圓外一點到圓上一點的距離的最小值.連接點B′和圓心O,交圓O于點A,交直線l于點C,點A,C即為所求點.
思路二:直線型拓展模型將點A所在的直線看作“定”的整體,在這個問題中,同樣用到整體思想,我們也可把點A所在的圓O看作“定”的整體.類比思路一的方法,如圖10,作定圓O關于直線l的對稱圓O′,連接BO′,交圓O′于點A′,交直線l于點C,作點A′關于直線l的對稱點A,點A,C即為所求點.此問題利用“兩點之間線段最短”來證明,理由從略.
0
進一步用運動變化的觀點,從特殊到一般的思想去思考:若點A,B在兩個不同圓上呢?學生作圖進一步探究.
問題3 如圖11,若點A為圓O1上一動點,點B為圓O2上一動點,圓O1與圓O2在直線l的同側,C為直線l上一動點,則點A,B,C分別在何處時,AC+BC的值最小?
1
2
解法指引:
點A,B在不同的圓上,點C在直線l上,三點都是動點,圓O1,O2均在直線l的同側,可以類比前面的問題2,用整體的思想,把圓O1,O2分別當作一個整體,看作直線l的同側的兩個不同的“定點”,就可以轉化為前面的將軍飲馬模型加以解決.如圖12,作圓O1關于直線l的對稱圓O′1,連接O′1O2交圓O′1于點A′,交圓O2于點B,交直線l于點C,連接O1C,交圓O1于點A,此時AC+BC的值最小,點A,B,C即為所求點.當然也可作圓O2關于直線l的對稱圓,方法與前面類似.此問題的證明方法也可類比將軍飲馬問題,如圖12,在直線l上任取一點C′,連接O1C′,O1′C′,利用“三角形中兩邊之和大于第三邊”來證明,具體證明略.有了此題問題的解決方法,以下2013年重慶高考題很容易找到突破口.
例2 (2013\5重慶高考)已知圓C1:(x-2)2+(y-3)2=1,圓C2:(x-3)2+(y-4)2=9,M,N分別是圓C1,C2上的動點,P為x軸上的動點,則|PM|+|PN|的最小值為(? ).
A.52-4
B.17-1
C.6-22
D.17
3
解析:
M,N分別是圓C1,C2上的動點,均在x軸的同側,問題歸類為以上將軍飲馬.聯系圓拓展模型,類比問題3的解法,如圖13,作圓C1關于x軸的對稱圓A,圓心為A(2,-3),半徑為1,圓C2的圓心坐標(3,4),半徑為3,|PM|+|PN|的最小值為圓A與圓C2的圓心距減去兩個圓的半徑和,
即(3-2)2+(4+3)2-1-3=52-4.故選答案:A.
2.3 聯系拋物線生成
用分類的思想進一步思考,若點A與點B分別在直線和拋物線上呢?引導學生探究,數形結合思想,最后拓展成如下問題.
4
問題4 如圖14,若A為直線l: y=x+1上一點且在x軸上方,B為拋物線y=x2-4x+5上一動點,C為x軸上一動點,求AC+BC的最小值.
解法指引:
分析題中已知條件,可以看出,點A,B,C均為動點,且點A,B均在x軸的同側,問題轉化為將軍飲馬問題.類比前面的方法,如圖14,作直線l:y=x+1關于x軸的對稱直線l1,易求得直線l1的解析式為y=-x-1.求AC+BC的最小值就轉化為求直線l1:y=-x-1上的點到拋物線y=x2-4x+5的最短距離了,此時可以平移直線l1至直線l2,當直線l2與拋物線y=x2-4x+5有且僅有一個交點B時,求得此時直線l2的解析式為y=-x+114,點B的坐標為32,54.過點B作BA′⊥l1,垂足為點A′,A′B交x 軸于點C,作點A′關于x 軸的對稱點A,即AC+BC的最小值為A′B,可求得A′B=1528.
3 課例評析
3.1 點成線,線成體,強化知識間的聯系
本節“一題一課”型復習課在素材的選擇上具有重要意義,選擇具有生長力的問題,以一個問題為點,聯系前后知識,梳理相關知識點,以思想方法為線索,在逐步變式拓展推進中,將知識點與思想方法融合,形成了知識結構體系.
3.2 思想方法引導,課堂生成行云流水
在變式拓展過程中,用運動變化的觀點,從特殊到一般,以分類思想、整體思想、數形結合思想、化歸思想為引導,聯系直線、圓及拋物線進行變式拓展,層層深入,自然生成一節“一題一課”型復習課,最后解決問題的方法動中取靜,透過表象找到本質.
3.3 對比分析,學生思維得以呈現
數學學習的本質是學習思維方法、提高思維能力.在數學思想方法的引導下,變式拓展問題,分析對比變式拓展前后的問題對象的共同特征,思考能否將問題轉化為拓展前的問題加以解決,讓學生從思維的角度找到解決問題的切入點.如,本文中讓學生分析變式拓展前后問題對象具有的共同特征,某兩個對象都在直線的同側,都是求最值的問題.讓學生經歷對問題的思考、拓展、對比分析、探索、提煉的過程,發展學生思維.
4 結束語
由于篇幅所限,本文只闡述了用數學思想引導生成一節“一題一課”型復習課的過程及簡要評析,在具體教學實施過程中,可根據學情,創造性地變式拓展提問,合理有序地組織學生進行復習探究活動,讓學生在活動的過程中,數學思維、數學技巧和數學方法得到有效演繹,從而幫助學生積累數學活動經驗,總結解題方法和規律,提升數學思維能力.
參考文獻:
[1]鄭新發.用活教材資源 生成智慧課堂[J].數學通訊,2016(6):1-5.
[2]李玉琪.數學中的邏輯思維方法與形象思維方法 [J].數學通報,1994(2).
[3]G\5波利亞.怎樣解題[M].涂泓,馮承天,譯.上海:上海科技教育出版社,2018.

