巧用錯題本，提高初中生數學解題能力

廖曉興

[摘要]分析學生“連續犯錯”的根本原因，探討糾正“一錯再錯”的方法，引導學生正確認識錯誤，開展有效指導。歸納解題策略，提高解題能力。精準收集分析，提高糾錯實效。關注“一錯再錯”的糾正效果，巧用錯題本，提高初中生數學解題能力。

[關鍵詞]根本原因;認識錯誤;歸納策略;收集分析;建立錯題本

初中數學教學中，普遍存在低效、無效化現象，教學過程中，不難發現許多學生在練習、作業或者考試時，出錯的題在下一次還會繼續犯錯的現狀。為此，我作為成員加入深圳市羅湖區《利用“錯題本”提高數學教學效率的研究》小課題進行深入研究，研究發現：巧用“錯題本”，可有效糾正“一錯再錯”的現象，提高初中生數學解題能力。

一、“連續犯錯”的根本原因

學生出現“連續犯錯”現象的根本原因：一是學生在學習新知時，沒覆蓋重點、難點和易錯點，致使訓練存在缺失、遺漏，導致踩坑、丟分;二是學生沒有養成訂正錯誤、標記錯題和分類收集錯題的習慣;三是糾錯方法與途徑缺乏專業的指導;四是學生對知識點間的聯結能力弱，不能舉一反三。

二、糾正“一錯再錯”的方法

（一）正確認識錯誤，開展有效指導

大部分成績停滯不前的學生，學習和做題時都是停留在舒適區，滿足于已掌握的題目，這一類題目屬于無效成功。但是，學生的有效錯誤比無效成功更重要。在教學過程中，正確認識有效的錯誤，指導學生將以下兩類有效錯誤收錄到錯題本中：第一類是考前已掌握，但考試時狀態不佳犯錯的題目;第二類是考試時盲目猜測，但經過評講后，學生能掌握的題目。讓學生訂正錯誤時，多停留一段時間，讓大腦充分思維，理解題目考察的知識點和解題技巧。此外，為切實減負，對一些簡單易懂的錯題，不必要求重復訓練。而一些難度較大的題目，學生不易理解和糾錯的，將其記錄在錯題本中，必要時，應指導學生進行多角度的訓練，使學生得到有效的糾錯。

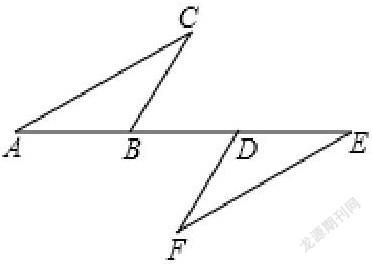
例如，基本式：如右圖，點A、B、D、E在同一直線上，AD=BE，BC//DF，∠C=∠F，試說明AC=EF。

由于AD和BE不是△ABC和△EDF的對應邊，證明△ABC≌△EDF時，學生容易出錯。

應引導學生先減去公共邊，AD-BD=BE-BD，即AB=DE。再使用AB=DE和其他條件（根據平行線的性質得出∠DBC=∠BDF，由等角的補角相等得出∠ABC=∠EDF，由全等三角形的判定定理）證明△ABC≌△EDF，最終得出對應邊AC=EF。

為達到糾錯效果，可通過下面的變式1、2進行多角度的訓練，由聯結公共邊證明三角形全等，并類比延伸到聯結公共角證明三角形全等。

變式1：已知點A、F、E、C在同一條直線上，AF=CE，BE//DF，BE=DF，求證：△ABE≌△CDF。

變式2：已知AB=AC，AD=AE，∠1=∠2，求證△ABD≌△ACE。

（二）歸納解題策略，提高解題能力

初中數學課程中，主要包括如下四大模塊。一是數與代數：實數、整式和分式（包括因式分解等）、方程和方程組、不等式與不等式組、函數等。二是空間與圖形：圖形的認識、圖形與變換、圖形與坐標、圖形與證明等（包括全等、相似、三角形、四邊形、圓等）。三是概率統計。四是實踐與綜合應用。在教學過程中，教師要引導學生對學習的各個新知識進行全面的歸納和梳理，讓學生掌握各個知識點、重點和關鍵點及知識體系等，并引導學生總結出相應的解題策略。如：一些特殊幾何問題，可通過畫輔助線、割補法及等量代換等。解決與圖像的選擇題，可運用數形結合法。求函數關系式時，運用待定系數法。因式分解中，運用拆項、添項法等……這樣，有助于學生對容易出現的各類錯誤進行糾正。此外，要指導學生進行各類題型的累加練習和一些特殊問題的練習等，讓學生見多識廣，不斷積累實踐經驗。實踐證明，通過上述方法，能有效地提高學生的解題能力，并減少解題錯誤。

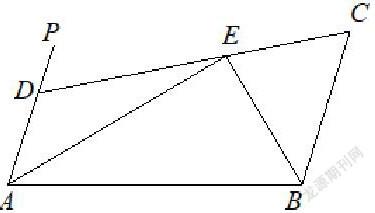
如右圖，AP//BC，∠PAB的角平分線與∠CBA的角平分線相交于E，CE的延長線交AP于D，試說明AB=AD+BC。

AD和BC是不在同一直線上的兩條線段，需要用三種方法等量代換：

1.全等三角形的兩條線段相等;

2.垂直平分線上的點到線段兩端的距離相等;

3.角平分線的點到角的兩邊距離相等。

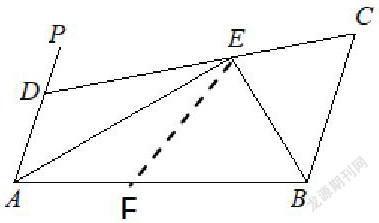
在AB上截取AF= AD，根據角平分線的性質證明△DAE≌△FAE。

結合等角的補角相等及平行線內錯角相等的性質，分別可得出：∠PDE=∠EFB，∠PDE=∠ECB，從而，可證△BFE≌BCE，得BF=BC，因此，AB=AF+BF=AD+BC，利用全等三角形的兩條線段相等，等量代換，證明等式。

（三）精準收集分析，提高糾錯實效

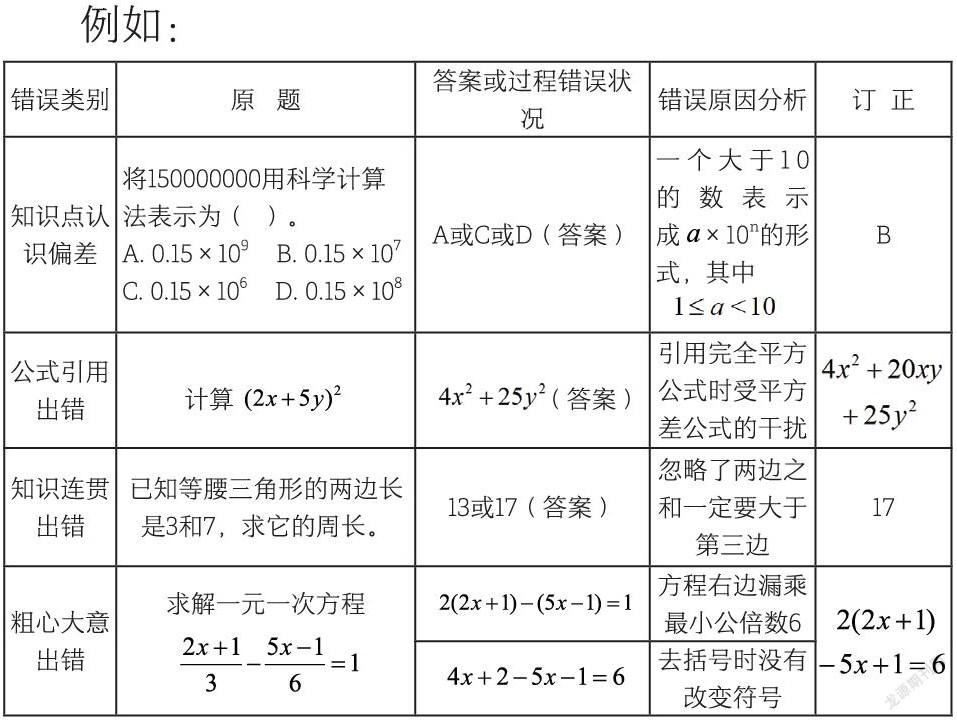
教學實踐中發現，學生容易出現的錯誤形式：1.知識點認識偏差。2.公式引用出錯。3.知識連貫出錯。4.粗心大意出錯（抄錯數字、上下前后答案對調、漏算、計算失誤等）。為了對分類收集錯題進行專業指導，我的做法是：不僅要針對普遍出現的錯誤進行收集，及時匯總個人重復犯錯的誤區，還要對壓軸題的解題思路進行梳理等。引導學生針對性地選擇錯題進行記錄，分析出錯的原因，并將其“抄”下來，明確其易錯類別，分析錯誤的原因，訂正錯誤，并建立錯題本。學生的學習過程，就是不斷充實和完善自我的過程，通過上述長期訓練，能有效地培養學生審題能力和對錯誤的辨析能力、分類能力、文字表述能力等，同時，要注意引導學生學會“舉一反三”，靈活運用，為糾正“一錯再錯”夯實基礎，最后達到預防直至避免錯誤。

例如：

三、“一錯再錯”的糾正效果

基于德國心理學家艾賓浩斯研究發現的遺忘曲線，在研究過程中，對學生答題出錯的現象和再次出錯的原因進行復盤和分析，不難發現，沒有整理糾錯習慣的學生，仍然時有再現“一錯再錯”的現象。有建立錯題本習慣的學生，能及時得到總結和梳理，“一錯再錯”的現象明顯減少。實踐證明，巧用“錯題本”能取得良好的糾錯收效，能提高初中生數學解題能力。

數學家華羅庚曾說：新的數學方法和概念，常常比解決數學問題本身更重要。在教學過程中，教師要對學生進行專業指導，歸納解題策略，引導學生分類收集有效錯誤，建立錯題本，通過巧用錯題本，能有效提高初中生數學解題能力。