專科護士陪伴式護理在小兒先天性多指(趾)畸形手術治療中的應用
朱玉婷 王哲 王瓊
山東大學齊魯醫院小兒外科,濟南 250000
多指(趾)畸形又被稱為重指(趾),主要發生在手足部位,多發生于嬰幼兒群體,是一種較常見的手足部先天畸形〔1〕。該類疾病雖對患兒手足功能的危害相對較低,但會嚴重限制其手足部位的正常發育,影響美觀,對患兒家屬也會造成不同程度的心理負擔〔2-6〕。手術是其重要的治療手段之一,圍術期的護理干預對于患兒的臨床療效非常重要。目前,社會人群對于醫療服務質量的要求不斷提高,常規的護理干預逐漸體現出部分局限性,如護理細節不完整、護理內容過度流程化等〔7〕。尤其對于手術患兒,因術后疼痛等影響,患兒會出現哭鬧、躁動等不良情緒,影響術后恢復。而常規護理針對性系統干預的措施嚴重缺乏〔8〕,從而導致其無法滿足患兒的基礎治療與康復需要,受此類原因影響,專科護士陪伴式護理模式開始逐漸形成。專科護士陪伴式護理是指手術前、手術期間和手術后為患者提供全方位的護理支持,從而提高手術的安全性和護理效果,優勢在于其全面性、個性化和協同性。本研究擬進一步了解該模式在小兒先天性多指(趾)畸形手術治療中的臨床應用效果。
1 資料與方法
1.1 一般資料
本項研究為隨機雙盲試驗,根據隨機試驗設計計算樣本量。納入山東大學齊魯醫院2020年1月至2021年12月收治的96例先天性多指(趾)畸形手術患兒作為觀察對象,患兒其他身體機能正常,無其他合并癥。納入標準:①符合手術適應證,且需進行手術治療;②年齡≤7歲;③患兒家屬均已簽署知情同意書。排除標準:①患兒自身存在傳染性疾病;②合并嚴重心、肝、腎等臟器功能不全;③合并心血管畸形。采用隨機數表法,按照1∶1的比例分為對照組、觀察組各48例。組間一般基礎資料比較差異無統計學意義(P>0.05),見表1,具有可比性。研究內容申報院內醫學倫理會審核通過(編號:20210376)。

表1 兩組一般資料比較(n)
1.2 研究方法
1.2.1對照組 予以常規護理干預。首先針對患兒多指(趾)部位予基礎檢查,了解其病情的基礎狀態,同時建立電子檔案,內容包括患兒姓名、性別、年齡、多指(趾)部位等內容,隨后上傳至本院醫療系統;主治醫師擬定治療手術方案,由護士告知患兒家屬相關治療流程以及注意事項,在此階段與患兒保持交流,通過玩具、音樂、視頻等方式分散患兒注意力,減輕患兒緊張情緒;待患兒情緒穩定后開始進行手術,術中嚴密監測患兒的生命體征變化,術后予以常規看護管理,如病房清潔消毒、營養補充、藥物支持、抗感染治療等,直至患兒康復出院。
1.2.2觀察組 予以專科護士陪伴式護理〔9〕,干預時間為30 d,具體護理內容如下:
1.2.2.1術前 患兒入院后,指定責任護士負責看護,逐漸增強患兒對護士的信任感,改善患兒的住院環境,張貼患兒喜歡的易撕兒童海報,改善患兒的緊張狀態。白班時,每間隔6 h進行一次病房尋訪,時刻關注患兒的情緒變化與生命體征變化;如患兒存在流涕、咳嗽、躁動等特殊情況需延長等待手術時間。同時,為患兒提供營養豐富的食物,嚴禁辛辣油膩飲食,防止患兒腹瀉。每天進行一次多指(趾)部位清洗。術前6 h禁飲禁食,由護士輔助患兒盡量排便。向患兒家屬分享治療成功的案例,增強治療信心,待患兒各項生理體征符合手術標準后開始進行手術。
1.2.2.2術中 手術期間,專科護士從旁陪護,手術室準備童趣互動工具,例如遙控小汽車、視頻動畫、可以播放兒歌的玩具等,承諾患兒在術后將上述玩具全部作為小獎勵給予患兒。每間隔5 min檢查一次相關手術設備,如手術刀片、可吸收線、醫用鉗等;同時,予以患兒柔軟肩墊,開展心電監護。護士需嚴格管理醫療器械,將雙極電凝、醫用鉗、整形鑷等進行合理擺放。確保無菌操作。在主治醫師完成手術后,將切除的多指(趾)部位放置于醫用托盤當中,妥善保存。
1.2.2.3術后 術后,將患者轉運至看護病房。取患兒平臥位,頭部偏向左側,嚴密監測其呼吸、心率等生命體征變化;同時,每間隔2 h進行一次排痰處理,保持患兒呼吸道暢通;做好保暖工作,覆蓋輕薄被子,減輕患兒軀體壓力;抬高患肢,利用醫用束縛帶或石膏進行固定。待患兒完全蘇醒后,通過疼痛評估方法,了解患兒的術后疼痛感;結合病情予以相應的鎮痛護理,方法包括分散注意力、藥物鎮痛等,護士可演繹患兒感興趣的動畫情節,講述兒童故事,并通過與其進行唱兒歌、小游戲等方式轉移其注意力,在此基礎上輔助患兒完成系統的康復訓練。
1.2.2.4出院 待患兒病情穩定且符合出院標準后,告知患兒家屬相關生活注意事項,同時建立院后交流跟蹤平臺,如微信群,與其時刻保持交流,及時了解患兒病情發展情況;耐心解答患兒家屬疑問,并提供相應的改善建議,叮囑復查時間。建立獨立的小兒先天性多指(趾)畸形康復公眾號,定期推送手術相關知識、術后恢復注意事項以及日常防護等內容的宣傳視頻。同時,由專科護士拍攝模擬康復訓練方法,例如患肢伸拉、腕關節與踝關節轉動等,每日堅持訓練10 min,直至患兒能夠自行完成。
1.3 觀察指標
1.3.1相關時間指標 由專人精確記錄兩組手術時間、術后復蘇時間以及住院時間。
1.3.2患兒術后疼痛程度 使用兒童疼痛評估量表法(FLACC)〔10〕評估患兒術后1、2、3 d的疼痛程度。通過觀察患兒表情、肢體動作、行為、哭鬧情況以及可安慰性等5方面進行評估,滿分為10分,分數越高代表疼痛感越強烈。該評分量表的Cronbach α系數為0.821 5~0.952 6。
1.3.3并發癥發生率 精確兩組入院30 d內的并發癥發生情況。
1.4 統計學分析
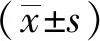
2 結果
2.1 兩組相關時間指標比較
觀察組患兒手術時間、術后復蘇時間、住院時間均低于對照組,差異均有統計學意義(均P<0.05),見表2。
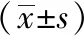
表2 兩組相關時間指標比較
2.2 兩組術后不同時間段的疼痛程度比較
重復測量方差分析顯示,兩組護理方法對患兒疼痛程度的影響存在交互、組間、時間效應,差異均有統計學意義(均P<0.05),見表3。
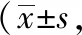
表3 兩組術后不同時間段的疼痛評分比較分)
2.3 兩組術后并發癥發生率比較
觀察組患兒出現關節僵硬、切口感染、靜脈危象各1例(2.08%),對照組出現關節僵硬5例(10.42%)、切口感染2例(4.17%)、靜脈危象3例(6.25%)。觀察組并發癥發生率[3例(6.25%)]低于對照組[10例(20.83%)],差異有統計學意義(χ2=4.360,P<0.05)。
3 討論
3.1 圍術期綜合護理可以縮短手術時間、術后復蘇時間和住院時間
多指(趾)畸形會嚴重影響兒童的心理健康,嚴重時還可能影響患兒的手足功能〔11-12〕。手術切除是治療這類患兒的常用方法,但是兒童心理發育不成熟,依從性較差,所以更加需要進行圍術期綜合干預。本研究結果顯示,觀察組手術時間、術后復蘇時間、住院時間均低于對照組,這與晉其云等〔12〕、賈飛飛等〔13〕的研究相符。其原因在于,專科護士陪伴式護理模式能夠將傳統意義上的護理措施進行細節優化與完善,主張護理的連貫性與綜合性,確保護理內容無縫連接,進而全面改善手術效果,實現縮短相關臨床時間指標的理想目的。
3.2 圍術期綜合護理可以減輕患兒疼痛、降低并發癥發生率
本研究結果還顯示,專科護士陪伴式護理管理模式對疼痛的改善效果更明顯,與溫雙娣等〔14〕、肖軍等〔15〕研究相符。說明該模式通過更加全面的疼痛管理,并聯合相應的康復鍛煉,可顯著緩解患兒術后不同時間段的疼痛感。干預后,觀察組患兒的并發癥發生率低于對照組,與代麗柯等〔16〕、曾秋茹等〔17〕的研究結果具有極高的相似性。由此可見,該護理模式能夠利用優質的術后跟蹤服務,時刻了解患兒病情的發展狀態,并為患兒家屬提供科學的護理方法與指導建議,最大限度地減少患兒的并發癥發生率。
本文還有以下不足:論文中可使用的樣本容量較小,導致結果的可靠性受到影響。下一步研究時,應該盡量增加樣本容量,以提高研究的統計學效力。
綜上所述,針對先天性多指(趾)畸形手術患兒,專科護士陪伴式護理能夠明顯縮短患兒的手術時間、術后復蘇時間以及住院時間,緩解患兒術后疼痛感,降低其術后并發癥的發生率,具有臨床推廣價值。

