一種抗能量分析攻擊的混沌密碼系統

羅玉玲，李天浩，肖丁維，丘森輝，3

（1.廣西師范大學電子工程學院，廣西桂林 541004；2.廣西多源信息挖掘與安全重點實驗室，廣西桂林 541004；3.廣西無線寬帶通信與信號處理重點實驗室，廣西桂林 541004）

如今，信息傳輸環境變得更加嚴峻，信息安全變得尤為重要，越來越多的學者參與到了密碼學這一研究領域中.為了提高信息傳輸的安全性，各種密碼算法被提出［1-4］，例如數據加密標準（Data Encryption Standard，DES），高級加密標準（Advanced Encryp?tion Standard，AES）.由于密碼學和混沌之間存在固有的關聯性（例如，對初始條件的敏感性，迭代結果的偽隨機性以及硬件實現的簡單［5-6］），使得混沌密碼系統成為一個可選方案.近年來，已經提出了許多基于混沌的文本加密［7-9］和圖像加密方案［10-14］，它們的安全性大多都是從數學、統計學特性進行分析的.然而從硬件角度來看，密碼系統在實際應用時，會泄露能量或時間消耗、電磁輻射等側信道信息［15-16］.側信道分析（Side Channel Analysis，SCA）就是分析這些側信道信息與數據或操作之間的相關性［17-18］.有學者證明常規的混沌密碼系統在實際應用中存在被破解的風險［19］，其設計的混沌密碼系統雖通過了常規的安全性能測試，但是硬件密碼系統在運行的過程中，不可避免地會泄漏能量.這些能量與加密操作中的中間數據有關，攻擊者則可以通過收集能量并進行分析攻擊從而得到敏感信息.

為了解決這類問題，本文提出了一種基于混沌的密碼系統，其在一個8 位微控制器上實現.在該系統中，由密鑰經過混沌映射生成輪密鑰與隨機序列數.隨后，將明文、輪密鑰與隨機序列數組合生成中間數據，使密鑰空間擴大了2128倍.此外，在該密碼系統中設計了四種加密操作順序，通過由隨機序列數生成的操作數控制，使得操作隨機化，以達到隱藏側信道信息的目的.并且，對中間數據進行了位級和字節級的擴散，提高了密文的擴散性能.最后，本文從常規安全測試和硬件安全兩個方面對其進行了安全性能分析.常規安全測試主要從字符頻率、隨機性、依賴性等進行測試，實驗結果證明，該密碼系統具有良好的安全性能.在硬件方面，利用相關能量分析（Correlation Power Analysis，CPA）攻擊方法驗證所提出的混沌密碼系統的安全性能.實驗結果證明，該密碼系統在完成加、解密的任務時，可以有效抵抗能量分析攻擊.

1 基礎知識

1.1 混沌映射

由于混沌系統具有良好的輸出遍歷性和對初始值的敏感性，所以目前經常用于密碼系統生成加密或解密所需的隨機數.基于眾所周知的陰影引理，許多人認為，通過迭代混沌映射生成的任何偽隨機數序列在很大程度上保留了原始混沌映射的復雜動力學.然而，研究者發現數字混沌映射的動力學肯定會退化到一定程度.了解數字計算機中混沌映射SMN的網絡結構，有助于在有限精度領域避免混沌動力學的不良退化，也有助于對混沌映射迭代生成的偽隨機數序列進行分類和改進［20］.

Logistic［21］和Tent［22］是非常經典的兩種混沌映射，并且具有良好的混沌效果，能滿足本文加密算法的需求，所以本文選擇使用Logistic 和Tent 兩種混沌映射，分別用于生成加密所需的輪密鑰和隨機序列數.本節將簡單介紹Logistic 和Tent 混沌映射的基本原理.

1.1.1 Logistic映射

Logistic 映射是一種應用廣泛的一維離散混沌映射.它被證明有良好的混沌性能，并且可以通過將初始值在[0，1]范圍內伸縮，從而生成[0，1]范圍內的混沌序列.它在數學上的定義式為

式中：a為控制參數，取值范圍為[0，4].

1.1.2 Tent映射

Tent 映射是另一種一維離散混沌映射.當其輸入值小于0.5時，將輸出擴展到[0，1]范圍內.當其輸出大于或等于0.5 時，Tent 映射會將其輸入值折疊到[0，0.5]的范圍內，然后再生成[0，1]范圍內的輸出.它在數學上的定義式為

式中：u為控制參數，取值范圍為[0，2].

1.2 分岔圖

分岔圖是將混沌的輸出序列隨著其初始值的混沌參數變化而引起迭代過程中輸出的變化可視化.圖1 給出了Logistic 和Tent 映射的分岔圖，可以看出，在整個參數范圍內，都會產生混沌現象.

圖1 分岔圖Fig.1 The bifurcation diagram

1.3 CPA攻擊

在密碼設備加密過程中，會生成一些與密鑰相關的中間數據.這些中間數據在處理時可能會通過能量、電磁等方式泄漏.CPA 攻擊是能量分析攻擊中比較強大的一種攻擊方法，它是利用了功耗與所處理數據之間的相關性，從而破獲敏感信息.

首先，攻擊者測量每次執行加密或解密操作時密碼設備產生的能量消耗.其次，攻擊者選擇一個中間值函數將明文或密文與假設密鑰相關聯起來，并以此函數來計算假設中間值，該函數的表達式為f(d，k)，其中d是明文或密文，k是密鑰的一部分.再次，中間數據通過能量模型轉化為假設能量消耗（常用的能量模型有漢明重量和漢明距離兩種）.最后，計算每個假設密鑰的假設能量消耗與實測能量跡之間的相關性，相關性最高的則為正確密鑰.用hd，i表示假設功耗矩陣中第i列的第d個元素，td，j表示實測功耗矩陣中第j列的第d個元素,和均表示均值.相關性計算公式為

2 密碼系統

該密碼系統在完成加、解密的任務時，可以有效抵抗能量分析攻擊.該密碼系統中采用的所有操作都是可逆的，所以是可以解密的.本節將對該密碼系統的結構和操作流程進行介紹.

2.1 操作流程

圖2 為提出的密碼系統的整體框架圖.其中每組明文和密鑰長度為128位，并將128位的明文和密鑰分為16字節.操作流程如下.

圖2 加密算法的總體結構Fig.2 The overall structure of encryption algorithm

第一步：根據每個密鑰字節，分別用Logistic 和Tent映射生成輪密鑰和隨機序列數.

第二步：將輪密鑰、明文和隨機序列數通過異或操作生成中間數據.其中隨機序列數也作為掩碼參與加密計算.

第三步：輪密鑰加操作.即每一輪新的中間數據與對應的輪密鑰進行異或操作.

第四步：隨機操作.對隨機序列數求均值得到操作數，通過依次對操作數從低二位到高二位進行判斷，然后選擇對應操作順序對中間數據進行加密.

第五步：進行擴散混淆操作.主要包括S 盒替換、移位異或、P盒換位等.

第六步：加密M輪后，形成密文.其中M的取值應該是合理的值，因為M太大的話，不僅會導致加密的時間過長，還會增加資源消耗成本，M太小的話，會導致密文的擴散和混淆性能不足.本文首先參考了以前研究者對加密輪數的取值［9，23］.此外，對于本文隨機操作中存在的四種情況，充分運用隨機序列數的每一位.基于此，本文將加密輪數M的值設為4.

2.2 輪密鑰和隨機序列數生成

每組輪密鑰由初始密鑰通過Tent 映射產生.首先將每組密鑰ki的范圍限制到[0，1]，并將其作為Tent映射的初始值xi，即xi=ki/255.

然后其初始值xi進行20 次迭代，并將得到的浮點數映射到[0，255]之間的整數，設第m組輪密鑰的第i個字節為xm，i，設輪密鑰為RK，則輪密鑰為

隨機序列數的生成與輪密鑰的生成操作基本一致，唯一不同的就是將Tent 映射改為Logistics 映射，設隨機序列數為RS，則隨機序列數為

Tent 映射和Logistic 映射參數的范圍分別為[0，2]和[0，4]，根據圖1 的分岔圖可知，Tent 映射的混沌參數r越接近2 和Logistic 映射越接近4 時，其混沌效果更好.本系統將Tent 映射的混沌參數r設1.999 887，Logistic 映射的混沌參數r設為3.999 888.將兩個混沌參數都設置為只有密文接受者才能知道的秘密參數.

相比于傳統的加密算法，攻擊者只需要猜測密鑰即可，本文由明文、輪密鑰和隨機序列數進行異或操作得到中間數據，其中隨機序列數不僅控制隨機操作，還作為掩碼參與加密操作.當攻擊者進行攻擊時，則需額外將掩碼計算在內，即擴大了密鑰空間.本文是對128 位的文本進行加密，掩碼也為128 位，所以密鑰空間從2128變為了2128×2128，即相比原本的密鑰空間擴大了2128倍.

2.3 掩碼操作

掩碼是保護加密系統免受CPA 攻擊的有效方法.它通過使用隨機生成的數字（掩碼）隱藏敏感數據，使功耗獨立于敏感數據.因為操作是基于屏蔽數據執行的，所以泄露的功耗與屏蔽數據相關，而不是與敏感數據相關，因此不可能利用功耗信息進行攻擊.

本文采用加性掩碼.掩碼由混沌映射產生.將中間數據a和掩碼m異或在一起，生成掩碼中間數據am，即am=a⊕m.如果屏蔽數據am是線性運算T的輸入，則輸出結果為

由于T()是一個線性運算，式（6）可以寫成T(am)=T(a⊕m)=T(a)⊕T(m).當需要去除掩碼時，即可以計算T(am)和T(m)之間的異或結果，即T(am)⊕T(m)=[T(a)⊕T(m)]⊕T(m)=T(a).

掩碼機制也存在一些缺點，特別是當一些中間數據用相同的掩碼隱藏敏感信息以減少掩碼的數量并加速操作時.例如，當中間數據a和b被相同的掩碼處理時，即am=a⊕m，bm=b⊕m.處理am和bm時的功耗分別表示為和它們與中間數據相關，即～(a⊕m)和～(b⊕m).差分功率也與am和bm的異或結果相關，因此功耗與中間數據a⊕b之間存在相關性.二階和更高階的DPA 或CPA攻擊可以使用這種相關性來進行攻擊［24］.為了克服這個限制，隨機操作被用來增強加密算法的安全性.

2.4 隨機操作

當執行CPA 時，首先需要對能量消耗數據進行對齊，即執行某一操作時產生的能量消耗可以定位到同一采樣點的每一條能量跡中.例如，在對密碼設備的一次能量消耗跟蹤中，第1 000個采樣點對應移位操作，對于其他的能量跡中，此采樣點也應對應于同一操作的能量消耗.如果能量消耗數據未對齊，則需要更多的能量跡來攻擊密碼系統［25］.其次，為了抵抗這種攻擊方式，可以通過將某一操作發生的時間隨機化這種方法來抵抗攻擊.例如，加密一個明文塊時，某個操作在第500 個系統時鐘執行，但是加密另一個明文塊時，該操作可能在第550 個系統時鐘執行.為了實現執行時間隨機化，添加隨機延時和操作順序隨機化是兩種常用的方法.然而如果添加太多的延時，會降低密碼系統的性能，因此本文選用后者以增強混沌密碼系統的安全性.本文設置了四種加密順序，在每一輪加密時，系統都會根據操作數來選擇具體執行哪一種加密順序.

首先對由初始密鑰經過Logistic 映射生成的隨機序列數求均值，得到一個操作數X，因為生成的隨機序列數每個值都在[0，255]，所以X的取值范圍也是[0，255]，然后將其轉化為一個八位的二進制，記為Xb.隨機操作的判定流程如圖3所示.

圖3 隨機操作判定流程圖Fig.3 The random operation judgment flow chart

每一輪加密對其中兩位進行判定，從最低兩位開始，然后每一輪左移兩位.每次判定會有四種情況，即00，01，10，11，因此該密碼系統設計了四種加密操作順序，以此對應于每種情況.例如，當情況為00 時，則執行第一種加密操作順序，情況為01 時，則執行第二種操作順序.該系統一共設置了四輪加密，每一輪判定兩位，四輪加起來剛好等于8 位，充分利用了Xb的每一位.

2.5 混淆和擴散

在密碼學中，混淆就是改變原本數據的值，使明文與密鑰的關系復雜化.擴散就是通過改變原本數據的值來將明文或密鑰的影響擴散到整個密文中［26］.它們分別通過置換和換位操作實現.例如：S盒置換和P 盒換位.本文使用S-P 網絡結構［27］，即交替使用置換和換位操作.在該密碼系統中，由于有四種操作順序，所以這里以00的情況舉例.

中間數據首先被S 盒替換混淆，S 盒是一個非線性替換表.本文采用的S 盒為AES 的S 盒，輸入一個[0，255]的值，經過S盒后替換成對應的值.

式中：di為S 盒的輸出，do為經過S 盒的輸出.然后使用向左移位的異或操作（LSX），將中間數據中的每個字節與其后續字節相關聯，即中間數據從高字節計算到低字節，最后一個字節保持不變.向右移位的加法操作（RSA）則相反，將中間數據與其前一個字節相關聯.即中間數據從低字節計算到高字節，第一個字節保持不變.中間數據的第i個字節用Si表示，將x向左和向右循環移位y位分別用函數SL(x，y)和SR(x，y)表示.則LSX和RSA的表達式為

為了要將每個字節的值控制在[0，255]內，所以在執行向右移位加法操作時，需要對其結果模256.

組合模塊一共包括三個操作，即P 盒換位、位序顛倒，以及位級移位.首先對得到的中間數據進行P盒換位操作.P 盒是通過隨機排列[0，127]的所有數字.在本文中，P 盒定義如表1 所示.即按照P 盒對128位中間數據進行重新排列.然后基于整個中間數據，即128 位，進行位序顛倒操作.位序顛倒操作為：將中間數據的第一位與最后一位的值互換，第二位與倒數第二位的值互換，以此類推.即

表1 P盒Tab.1 P-box

最后將128 位中間數據向左循環移動一位.即最后一位的值等于第一位的值，其他每一位的值等于后一位的值.得到一個新的中間數據.即

3 安全性能分析

本節選用廣泛使用的一些統計測試（包括字符頻率測試、信息熵測試、依賴性測試、SP 800-22 測試）來評估該密碼系統的安全性能.

3.1 字符頻率測試

在密碼學中，字符頻率是推測密鑰的重要途徑之一.一些替代密碼算法可以使用字符頻率來攻擊［28］.因此，字符頻率測試可以用來評價密碼算法的安全性能.一個良好的密碼算法所得到的密文分布應該是盡可能均勻的.本文將100 000 套（1 600 000 字節）隨機明文通過固定密鑰加密成密文，在加密過程中，明文和密文以ACSII 碼的形式存儲.然后對其明文和密鑰進行字符頻率計算.計算結果如圖4 所示.由圖4 可以看出，密文的ASCII 值大約都在0.003 9 左右，即1/256，分布十分均勻.因此，使用概率攻擊是很難破解該密碼系統的.

圖4 字符頻率測試Fig.4 Character frequency test

3.2 信息熵測試

熵最初是表示分子狀態混亂程度的物理量.后來，在密碼學中引入了熵的概念，即信息熵.信息熵被定義為離散隨機事件的出現概率.用p(xi)表示字節xi的ASCII值在整個密文中出現的概率，則隨機變量X的信息熵H(X)為

在理想狀況下，加密算法得到的密文分布是絕對均勻的，即p(xi)=1/256，i∈[0，255]，則等式可以轉換為

本文對不同字節數量的密文進行了信息熵的計算，并與其他論文提出的密碼系統進行了比較.如表2所示.

表2 信息熵Tab.2 Information entropy

當密文字節數為1 000 000 時，本文提出的密碼系統的信息熵為7.999 8，非常接近8.此外，無論密文字節數量是5 000或者10 000時，其信息熵都大于其他兩種密碼系統.這意味著該密碼系統具有良好的混淆性能.

3.3 依賴性測試

依賴性測試用來檢測密碼系統的擴散性.依賴性測試包括完備度dc、雪崩效應da和嚴格雪崩準則dsa三項測試指標.完備度是指密碼系統的任何輸出位都與所有輸入位有關.雪崩效應是指明文或密鑰的少量變化會引起密文的巨大變化.嚴格雪崩準則是指當任何一個輸入位被反轉時，輸出中的每一位均有0.5 的概率發生變化.計算這三個參數的方式如下.

具有n位輸入和m位輸出的函數表示為f：向量表示通過對向量第ith位進行補碼而獲得的.對第i位輸入位進行補碼導致第j位輸出位發生變化的輸入數為依賴矩陣A中第(i，j)元素，用ai，j表示，用函數#{}表示計算集合元素的數量，則ai，j為

同樣，對第i位輸入位進行補碼導致第j位輸出位發生變化的輸入數量為距離矩陣B中的第(i，j)個元素，用bi，j表示，用Hw(x)表示x的漢明重量，則bi，j為

通過上述的計算，完備度dc則可表示為

雪崩效應da為

嚴格雪崩準則dsa為

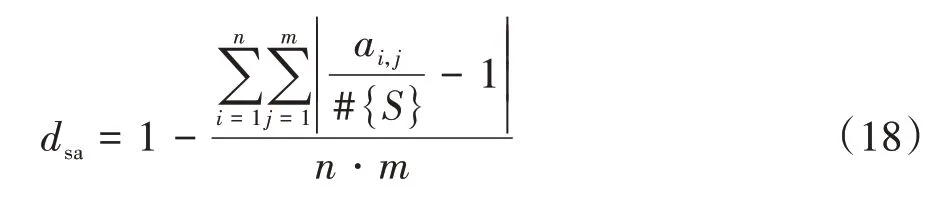
式中：S表示隨機選取的密文數量的集合.

根據加密輪數的增加的，對依賴性進行了測試，結果如圖5 所示.由圖5 可以看出，當在第四輪后，雪崩效應和嚴格雪崩準則值的變化趨于平穩，故本文將加密輪數M設為4.

圖5 不同輪數下da和dsa的值Fig.5 The values of da and dsa criteria in different rounds

一個出色的加密算法，應滿足dc=1，da≈1，以及dsa≈1.本文對所提出的密碼算法分析了10 000 000位隨機密文，通過上述公式計算得到測試結果分別為dc=1，da=0.999 77，以及dsa=0.997 478.并與其他論文提出的密碼系統進行了比較，結果如表3 所示.由表3 可以看出，所提出的密碼系統，在da和dsa上都優于所對比的其他密碼系統，即證明了該密碼系統有良好的擴散性能.

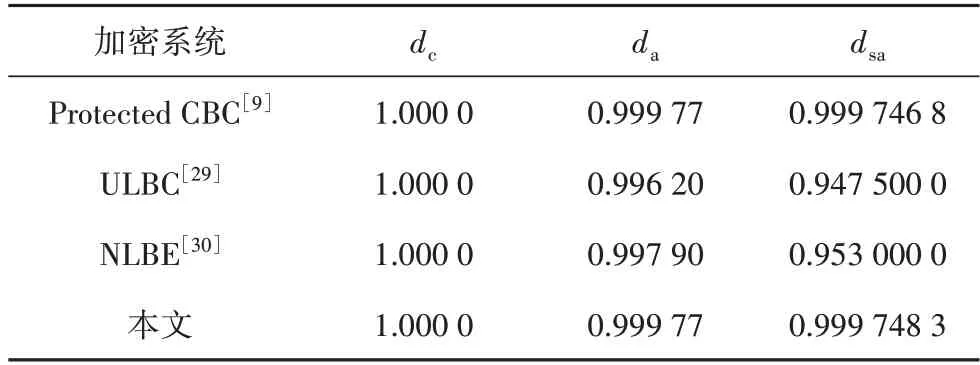
表3 依賴性測試結果Tab.3 Dependency test results

3.4 隨機性測試

在密碼分析領域，NIST 頒布了一種用于統計隨機數和偽隨機數的測試標準800-22（SP 800-22），它包括15 個測試項目.每個測試項目中，p值大于0.01則表示密碼算法通過了此項測試.一個加密算法如果能通過此測試，則表明它可以抵抗統計分析攻擊.本文對由隨機明文生成的10 000 000 位密文進行了測試，測試結果如表4 所示.由表4 可以看出，所提出的密碼系統通過了全部的15 個測試項目，證明了該密碼系統輸出序列的隨機性.

表4 SP 800-22 測試結果Tab.4 SP 800-22 test results

混沌系統的隨機性和遍歷性，可以有效避免弱密鑰的產生.傳統的一維混沌映射所迭代出來的序列可能是存在弱密鑰的，但是所提出的密碼系統并不是將經過迭代后的序列作為密文，而是經過了混淆和擴散操作后，生成密文.由字符頻率和隨機性等測試結果可知，所提出的密碼系統具有良好的隨機性能，即使輸入的隨機序列大多相同，生成的密文分布也是十分均勻的，即能夠有效避免弱密鑰的產生.

4 資源消耗及攻擊結果分析

4.1 資源消耗

本文設計的密碼系統通過Atmel XMEGA128-D4 微控制器實現，該芯片是8/16 位微控制器，時鐘頻率為7.37 MHz.然后與其他密碼系統進行了資源消耗對比，包括AES、CWSN［8］、Protected CBC［9］、CBC［19］、Masked AES［31］.本實驗通過數據內存、程序內存和時間消耗來衡量資源消耗.結果如表5所示.

表5 資源消耗Tab.5 Resource consumption

由于本文提出的密碼系統是基于混沌映射的，需要多次迭代計算，此外還有掩蔽和隱藏操作的存在，所以導致所提出的加密算法相比AES、CBC、CWSN，需要消耗更多資源.但是其時間消耗是小于CWSN 和Protected CBC 的.其中CBC 的混沌系統被證明不能抵抗能量分析攻擊與基于機器學習的能量分析攻擊［32-33］，Protected CBC 的混沌系統采用了掩碼的技術，雖然能抵抗能量分析攻擊［9］，但是相比本文所提出的混沌密碼系統，在數據內存、程序內存和時間上的消耗更多.所以本文設計的密碼系統在資源消耗上具有一定優勢.

4.2 CPA攻擊結果分析

為了進行CPA 攻擊，將該加密算法在Atmel XMEGA128-D4 微控制器實現，然后采集加密過程中的能量消耗.在這項工作中，采集了500 條由隨機明文、固定密鑰生成的能量跡.圖6 是能量跡中的一條.其中大概前1 700 個采樣點處于隨機數生成階段，1 700到2 800個采樣點則處于加密階段.

圖6 密碼系統的能量跡Fig.6 The power trace of the cryptosystem

首先采用一階CPA 對不同數量的能量跡進行攻擊，實驗結果如圖7 所示.由圖7 可以看出，即使隨著能量跡數量的增多，相比錯誤密鑰的相關系數，正確密鑰的相關系數隱藏在錯誤密鑰中，即無法通過CPA攻擊得出正確密鑰.

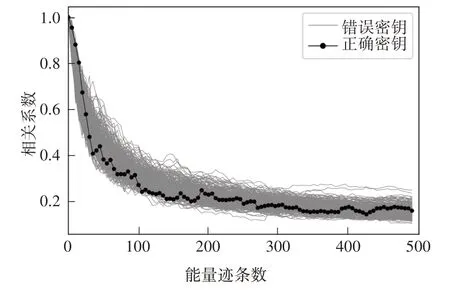
圖7 CPA攻擊結果Fig.7 CPA attack results

每個輪密鑰和一個操作數定義為一個假設組合，則中間數據的每個字節有216種假設組合.此外，由于該密碼系統設置了四種加密順序，所以攻擊者不能很好地確定攻擊點.假設每輪加密執行的是一種加密順序，且S 盒替換都是加密操作的第一步，則CPA的攻擊結果如圖8所示.

圖8 假設攻擊結果Fig.8 The result of the hypothetical attack

為了更直觀地了解攻擊結果，將相關系數排序，排序圖如圖9 所示.相關系數有了一個驟變到接近0.6 的過程，將該相關性的假設組合提取出來，發現一共有256 種可能，這意味著無法從最大的相關系數推斷出正確密鑰的組合.

圖9 假設攻擊結果排序圖Fig.9 The sorting of hypothetical attack result chart

但是在實際攻擊中，幾乎不可能存在這種加密情況，所以，本文做出了另一種假設，攻擊者默認第一輪加密都是執行S 盒替換，然后采用CPA 攻擊，攻擊結果如圖10所示.

圖10 隨機攻擊結果Fig.10 The result of random attack

可以看出，皮爾森相關系數僅在0.1 到0.25 之間，再將相關系數排序得到圖11.由圖11（a）可以看出：相關系數呈反雙曲正切函數分布，并且最大與最小的相關系數差異很小.然后將相關系數大于0.20的假設組合提取出來，如圖11（b）所示.可以看出最大概率與第二大概率相差不足0.02，且最大的皮爾森相關系數依然存在256 種可能，仍然是不能推斷出正確密鑰的組合.

圖11 隨機攻擊結果排序圖Fig.11 The sorting of random attack result chart

4.3 基于機器學習的攻擊結果分析

為了進一步驗證提出的混沌加密算法在抵抗能量分析攻擊中的效果，采用基于機器學習的攻擊方法［33］對該混沌加密算法進行安全性能分析.攻擊結果如表6所示.

從表6 可以看出，實際密鑰與攻擊所得的密鑰是不相同的.針對同一字節，攻擊所得密鑰與實際密鑰的相關性最小相差0.071 299，最大相差0.667 533.相差最小的情況下，實際密鑰在相關性中排名為17，所以無法得到實際密鑰.即該混沌密碼算法能夠很好地抵抗基于機器學習的能量分析攻擊.

表6 機器學習攻擊結果Tab.6 Machine learning attack results

5 結論

為了抵抗能量分析攻擊，本文設計了一種基于混沌的密碼系統.該系統利用兩個混沌映射Tent 和Logistic 分別生成輪密鑰和隨機序列數.中間數據由明文、輪密鑰以及隨機序列數處理后組成，使密鑰空間擴大了2128倍.同時由隨機序列數生成操作數，對執行操作進行隨機化處理，從而隱藏了側信道信息.此外，對于中間數據的處理基于位級和字節級擴散，這使得經過四輪加密后的擴散性能良好.實驗結果表明，該密碼系統能夠通過常規安全測試且具有較好性能，并且能成功抵抗CPA 攻擊.未來的工作是在提高密碼系統安全性能的同時，進一步減少硬件資源消耗與提高密碼算法的隨機性.