半實物射頻仿真的誤差聯合概率密度函數分析
唐 波, 劉乃文, 馬 靜, 郭琨毅, 盛新慶
(1. 北京科技大學計算機與通信工程學院, 北京 100083; 2. 北京仿真中心航天系統仿真重點實驗室,北京 100854; 3. 北京理工大學集成電路與電子學院射頻技術與軟件研究所, 北京 100081)
0 引 言
半實物射頻仿真是雷達導引頭系統研發過程中常用的一種測試方法,是介于外場試驗與全數字仿真之間的一種仿真技術,既在一定程度上克服了外場試驗所需費用較大的問題,又通過實物在回路而使仿真保持了相當高的真實度。現在世界上的一些主要國家和大型研發公司,都建立有半實物射頻仿真實驗室。例如英國的馬可尼公司、美國的埃格林空軍基地導彈仿真實驗室、陸軍高級仿真中心等。我國也在相關科研院所建立了半實物射頻仿真實驗室。半實物射頻仿真微波暗室中,多個輻射天線單元整齊排列,構成天線陣列墻。微波暗室的另一端是一轉臺,可以將待測雷達導引頭系統置于其上。為了仿真某一方向過來的點目標回波,可以使用在方向上包圍該點目標的相鄰的3個輻射單元。這3個輻射單元構成了一個三元組。通過調整三元組中每個輻射單元的饋電幅度,可以模擬該點目標在三元組構成的三角形內不同方向的回波,從而可以快速地仿真點目標在運動軌跡上每個位置處的散射回波。三元組仿真的目標方位位置可以由重心公式給出。
對于半實物射頻仿真,相關的研究文獻目前主要關注以下幾個方面:仿真誤差分析,近場誤差與近場修正,仿真對象的擴展,仿真誤差的抑制等。例如,文獻[4]研究了仿真的實時控制技術,文獻[5]研究了寬帶雷達的射頻仿真問題。由于器件以及模型的非理想性,射頻仿真不可避免地存在誤差。文獻[7]使用統計方法對射頻仿真系統的誤差以及可靠性進行了分析。文獻[8-9]建立了射頻仿真誤差模型。文獻[10-11]研究了近場效應、近場誤差的產生以及近場修正算法。文獻[12]研究了對多個散射中心進行半實物射頻仿真的問題和誤差分析。文獻[13]提出使用分集的方法來抑制仿真誤差。文獻[14-15]研究了幅度相位誤差對仿真誤差的影響。文獻[16]研究了天線方向圖、轉臺誤差等對仿真誤差的影響。文獻[17]從不同象限的天線接收信號強度著手對三元組近場誤差進行了修正。文獻[18]研究了耦合對半實物射頻仿真角度誤差的影響。文獻[19]研究了近場效應對仿真精度的影響。文獻[20]給出了比幅單脈沖導引頭仿真的近場修正表格。上述對半實物射頻仿真誤差的研究多從方位角誤差和俯仰角誤差分別進行研究,而沒有考慮到這兩個不同角度域上誤差的相關性;或僅考慮二維角度誤差幅值的均方根,而沒有考慮角度誤差的方向性分布。
隨著雷達技術的精進,對其半實物射頻仿真誤差的評估需要更精確地進行。仿真角度誤差是評估半實物射頻仿真系統的一個重要指標。因此,為了對仿真角度誤差進行更精確地描述,需要對其在二維角度域上的聯合概率密度函數(probability density function, PDF)進行研究。
因此,本文將從常見的饋電幅度誤差著手,研究其導致的仿真角度誤差在二維角度域上的聯合PDF分布。
1 三元組仿真的數學坐標系
半實物射頻仿真通過3個相鄰的構成正三角形的3個輻射單元,按照一定的幅度比例對3個單元進行饋電,其在空間中疊加生成的總的輻射場在轉臺處的能流密度或相位梯度沿著真實點目標的視線方向,從而仿真該點目標的散射回波。為了研究方便,建立如下坐標系:以轉臺位置處為坐標原點,轉臺與三元組的中心點的連線為軸,三元組的底邊與軸平行,三元組所在平面平行于面。

圖1 三元組仿真數學坐標系Fig.1 Coordinates system of three-unit-array simulation
三元組3個單元的坐標為(,,),=1,2,3,在球坐標系下表示為(,,),=1,2,3。將直角坐標(,,)對距離歸一化,得

(1)

(2)
同樣,可得目標的關于距離歸一化的直角坐標為
=sincos
(3)
=sinsin
(4)
=cos?1
(5)
則可定義目標在和方向(也即和方向)的角位置分別為
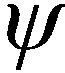
(6)
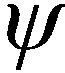
(7)
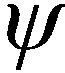
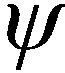

(8)

(9)
式中:(=1,2,3)為3個輻射單元的饋電系數,為實數。已假定各單元初始相位調整為同相。由重心公式,通過常規的矩陣求逆即得饋電系數關于單元位置和仿真點位置的表達:

(10)

(11)

(12)

2 仿真誤差的二維聯合PDF
在進行半實物射頻仿真時,由于器件性能和噪聲的限制,各單元的饋電幅度不可能絕對精確,而是會存在一定誤差,即、、存在誤差。該幅度誤差將會導致仿真給出的目標位置產生誤差。若、、的誤差記作Δ、Δ、Δ,則通過常規的偏微分運算可由式(8)得到方向上的仿真誤差為

(13)
式中:

(14)
同理:

(15)

(16)
將式(14)~式(16)代入式(13),得

(17)
同理可得方向仿真誤差為

(18)
由于Δ為饋電幅度誤差隨機變量,因而Δ和Δ也為誤差隨機變量,則ΔΔ的均值為

(19)


(20)
即

(21)
將式(21)代入式(19),得

(22)
另外,和方向上的仿真角度誤差方差為

(23)

(24)
則可由式(22)~式(24)得Δ和Δ的相關系數為

(25)
從而Δ和Δ的聯合PDF可以表示為

(26)
二維聯合PDF的對稱軸相對于軸的偏移角為

(27)
這表明,相關性的存在將會導致二維PDF的分布產生傾斜。
可以用長短軸之比

(28)
來表達仿真角度誤差在方向上差異性的大小,以定量評估在航跡方向以及垂直航跡方向的角度誤差之比的極值。
3 相關性與方差分析
首先討論一個特殊的待仿真點目標位置,即點目標處于三元組三角形中心的情況。此時==0,代入式(25)得

(29)
對于中心點目標,由于==,則式(29)可進一步化簡為

(30)
將圖1中給出的三元組各單元坐標代入可得=0。這表明,中心點處的仿真角度誤差在和兩個方向上不存在相關性。事實上,不論對圖1所示坐標系如何旋轉和平移,該結論都是成立的。這可由式(25)出發來獲得證明。由于(,)為三元組的中心點,因而可以記:
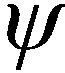
(31)
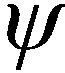
(32)

(33)

(34)

(35)

(36)
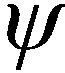

(37)
另外,可將式(31)~式(36)以及==代入式(23)和式(24),得

(38)

(39)

因而,在三元組中心點處,任意兩個正交方向上的仿真角度誤差皆不相關,且方差相等。
下面再對三元組內部對稱軸上的點目標仿真角度誤差進行分析。若點目標處于過單元1的對稱軸(軸)上,則此時==0,-=-(-),-=-,=,代入式(23)~式(25),得

(40)

(41)


(42)

若點目標處于過單元2或單元3的對稱軸上,則此時=或=,代入式(25),可知一般不為零。
以上為三元組內部點目標的仿真角度誤差情況。對于處于三元組3條邊上的點目標,其仿真角度誤差PDF分布將退化成一維的情況。此時,仿真角度誤差的PDF為沿著點目標所在三元組的邊的分布函數,即聯合PDF由面分布退化成了線分布。此時,由于仿真角度誤差沿著一條確定的直線分布,因而Δ和Δ之間存在一個確定的線性關系。記:
Δ=Δ
(43)

4 數值結果
下面對上述解析分析結果作數值仿真計算。仿真所用坐標系亦如圖1所示。三元組邊長張角為=36 mrad,幅度相對誤差的均方根為=002。針對(,)取值依次為(0003,0001 7)、(-0003,0001 7)、(0,-0003 5)、(0,0006 9)、(-0006,-0003 5)、(0006,-0003 5)、(0006,0003 5)、(-0006,0003 5)、(0,-0006 9)、(0,0013 9)、(-0012,-0006 9)、(0012,-0006 9)的12個待仿真點目標位置進行二維仿真角度誤差聯合PDF計算。這12個位置如圖2所示。這12個位置實際上處于尺寸為三元組1/3和2/3的兩個正三角形上,且處于三元組的3個對稱軸上。圖3給出了第8個位置處仿真角度誤差的聯合PDF三維圖。可以看到,聯合PDF的對稱軸相對于軸產生了傾斜。為了更好地觀察仿真誤差聯合PDF的分布,圖4給出了等值線圖。圖4(a)~圖4(l)分別依次給出了目標所在位置為第1~12處的仿真誤差聯合PDF的等值線分布。可以看到,位置1、2、5、6、7、8、11、12處的PDF產生了傾斜,其等概率密度線橢圓的對稱軸偏離了軸;而位置3、4、9、10處并沒有產生傾斜。注意到,位置3、4、9、10正處于三元組的對稱軸軸上,而此處相關系數為零。另外,2、5、8、11向著同一側傾斜,1、6、7、12向著同一側傾斜。這是因為軸右側的區域相關系數為負,而左側區域的相關系數為正。對比1、2、5、6和7、8、11、12可以看到,越偏離軸,橢圓越扁。

圖2 仿真目標位置示意圖Fig.2 Locations schematic diagram of the simulated targets

圖3 目標位置8處仿真誤差PDFFig.3 PDF of simulation error at location 8


圖4 二維誤差聯合PDF分布圖Fig.4 Two-dimensional error joint PDF distribution
雖然在推導誤差二維分布函數的過程中設立了具體的坐標系,然而在幅度重心公式的研究框架下,誤差二維分布函數在三元組中的分布圖與坐標系的選擇無關。仔細觀察圖4,這12個點的誤差分布圖正如其在三元組中的位置一樣,具有120°的旋轉對稱性,這與坐標系的選擇無關。
為了更全面地考察整個三元組內部各點處的仿真誤差PDF的特點,圖5給出了三元組內部各點處的和兩個方向上的仿真角度誤差的相關系數分布。圖5(a)給出了三維圖,圖5(b)給出了等值線圖。由圖5可以看到,相關系數在軸上為零,由軸向兩側的兩條邊,相關性逐漸增大。向右側邊是負相關增強,向左側邊是正相關增強。相關系數的分布是隨坐標系的選取而變化的,因而此處結果僅針對本文坐標系。

圖5 相關系數分布Fig.5 Correlation coefficient distribution
5 結 論
本文通過解析分析和數值計算,給出了半實物射頻仿真的仿真角度誤差的聯合概率密度分布。在三元組的3條中線上誤差橢圓的長短軸分別平行于三元組的中線與其對應邊。三元組外,在三元組中線延長線上的誤差橢圓分布也有相同的規律。通過對其有關參數——相關系數和方差進行研究,給出了其分布特點。在三元組中心點處,任意兩個正交的方向上其仿真角度誤差不相關,且任意兩個正交方向上的誤差方差相等,其聯合PDF的等值線分布圖是一系列的同心圓。當某個坐標軸為三元組的某個對稱軸而另一坐標軸與三元組一邊平行時,在該對稱軸上的各點處,兩個坐標方向上的仿真角度誤差不相關。且由該對稱軸分別向兩側,即兩個坐標方向上的仿真角度誤差的相關性越來越強。在該對稱軸的兩側,聯合PDF的等值線橢圓產生傾斜,且離開該對稱軸越遠,橢圓越扁,直到在左右兩個側邊上收縮成一條線。

