盾構隧道施工引起地表沉降的“五維”空間效應探索及其展望

于廣明，雷 軍，張鵬輝，陳 澤，梁冠文

(1.青島理工大學 土木工程學院，青島 266525；2.中國建筑第五工程局有限公司，長沙 410007；3.中國建筑五局華南公司，廣州 510000)

1 問題的提出

地鐵的建設既為現(xiàn)階段人們的出行提供了方便，也為將來城市地下空間的統(tǒng)一規(guī)劃和建設留下伏筆。然而，地鐵隧道施工過程中不可避免地會對地層產生擾動，造成地表沉降等地質災害，無論是對于地下管線還是地面已有建筑物都有不容忽視的影響，在某些復雜地質條件下甚至會造成更大的危害，如圖1所示，社會危害和經濟損失極其嚴重，已成為當今社會的熱點問題和隧道施工安全的重大難題，迫切需要地鐵隧道施工引起的地表沉降安全管控的分析理論與方法。因此，研究隧道施工引起地表沉降的機理和規(guī)律，進而在此基礎上研制隧道施工引起地表沉降的控制措施，社會效益、工程價值及其科學意義均十分明顯。

圖1 隧道施工引起地表沉降的危害

對于隧道施工引起的地表沉降特性及發(fā)展演化規(guī)律問題，國內外學者已有一定研究，PECK[3]在總結大量現(xiàn)場實測數(shù)據(jù)的基礎上提出地表沉降滿足高斯正態(tài)分布曲線，且認為地表沉降現(xiàn)象是由地層損失導致的，在不排水的條件下地表沉降槽體積與地層損失體積相同；劉寶琛等[4]對波蘭學者LITWINISZYN提出的隨機介質理論進行了進一步擴展，將巖土體當作一種隨機介質，建立了地表沉降計算的概率積分法，解決了地下開挖引起的地表沉降預測問題；王璐[5]研究了盾構隧道施工步長對地表沉降槽形狀的影響，得出大步長的沉降量相比小步長的沉降量大的結論；趙旭偉[6]研究了地層變形的空間效應和時間效應，分析了在時間軸上地表沉降槽的發(fā)展歷程；侯學淵等[7]通過將固結效應引起的附加沉降作為地層損失的一部分，對Peck公式做出修正，將地表沉降槽隨時間的演化規(guī)律通過公式的方法進行了描述；AHMED等[8]通過透明模型試驗模擬了隧道開挖過程，并認為受擾動的巖土體顆粒位移矢量指向隧道軸線下方仰拱附近或隧道中軸線方向。夏元友等[9]通過使用位移矢量方法研究了盾構施工引起的地表土體水平位移特性，在驗證了AHMED結論的正確性后，又提出了位移矢量角的概念。高守棟等[10]研究了地面出入式盾構隧道對周圍地層的擾動效應，驗證了地面位移與空隙水壓力之間的變化關系。秦東平等[11]利用三維非線性有限元模型和相關解析理論，研究了地鐵修建過程中地表變形規(guī)律。然而，上述學者多數(shù)是在X，Z兩個維度或X，Y，Z三個維度上分析和認識隧道施工引起地表沉降的展布，在三維空間中將盾構隧道施工引起地表沉降視為槽型，稱之為地表沉降槽，研究沉降槽在橫剖面和縱剖面上的幾何特性，例如Peck公式研究的是地表在不排水條件下沉降槽在橫剖面上的幾何特性，對于沉降槽形狀隨步長和時間的演化則沒有描述；少數(shù)學者對隧道施工引起地表沉降的時間效應進行了研究，初步涉及了隧道施工引起地表沉降在X，Y，Z，T四個維度上的演化問題。

但是，現(xiàn)場工程實踐證明，如深圳地鐵13號線留仙洞—白芒區(qū)間盾構隧道施工，地表沉降除了在X，Y，Z三個維度上展布且隨著時間T維度發(fā)展以外，還隨著掘進步長L這個維度不斷地演化，若想更加深入、更加精細認識和研究隧道施工引起地表沉降的復雜性，需要根據(jù)盾構隧道施工的特點及其引起地表沉降的真實過程，進一步研究地表沉降在掘進步長L維度和時間T維度上的演化特征和規(guī)律。因此，本文擬將隧道掘進步長L維度和時間T維度分離，探究地表沉降隨盾構隧道掘進步長和時間兩個維度的演化規(guī)律，揭示盾構隧道施工引起地表沉降的“五維”空間效應。

自然界中“五維”空間是否存在，能否在“五維”空間中認識和研究自然現(xiàn)象，目前仍是科學之謎，在這方面只有少數(shù)科學家有過揭示和研究，WESSON等[12]通過對電磁與引力兩大基本力統(tǒng)一模型的研究，將廣義相對論延申至五維空間，并得出一個五維度規(guī)張量的純量場；PRATEEK等[13]通過對實驗中微粒的觀察，發(fā)現(xiàn)有部分微觀粒子躍遷到了人類“看不到的空間”，它們其實離我們并不遙遠，只是很好地隱藏了起來，PRATEEK將這個“我們看不到的空間”稱為“第五維空間”。可見國際上學術界對“五維”空間的認可。所以，就自然現(xiàn)象的空間維度來講，可以肯定地說“分維是真例，整維是特例；三維、四維是暫時的，多維(分維、大于四維)是長遠的”，地表沉降現(xiàn)象的分維特征和多維性是其存在的必然，建立盾構隧道施工引起地表沉降的空間-步長-時間“五維演化理論”將成為可能[14]。

2 盾構隧道施工引起地表沉降的維度問題

2.1 地表沉降的二維闡述

隧道施工引起地表沉降是被擾動波及的地表上所有點的群體位移效應，不過最初為了工程方便或研究手段的限制，只分析隧道橫剖面上地表點的位移，即沉降曲線，如圖2所示；對某個地表點來講，其位移為指向隧道中心的矢量，分為沿垂直方向(Z)的“下沉”和沿水平方向(X)的“水平移動”。同理，對于隧道縱剖面上地表點的沉降表示也僅分析沿垂直方向和水平方向兩個維度的沉降曲線，此時一般只研究沿隧道中心線的縱剖面上地表點的沉降，如圖3所示。

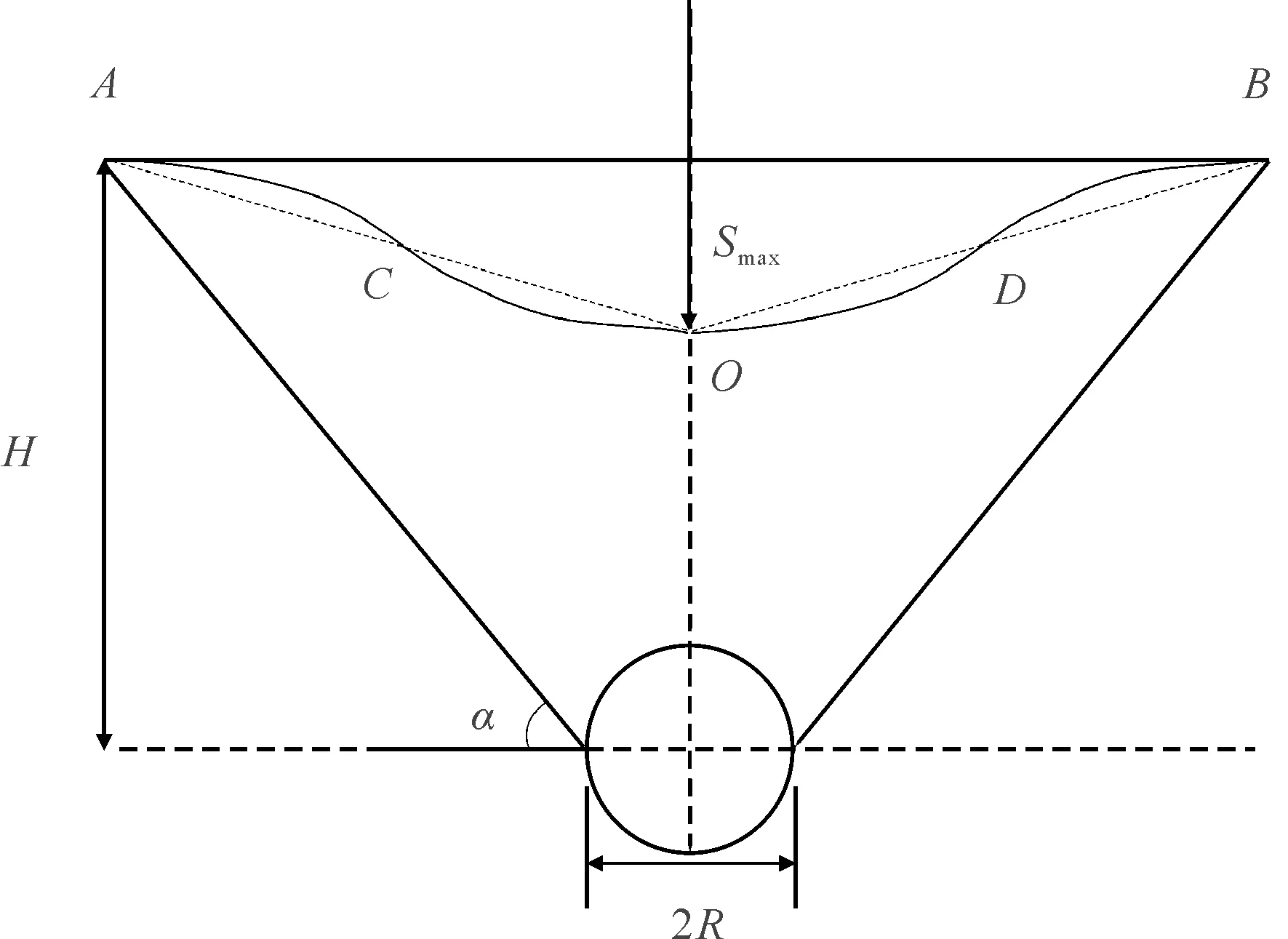
圖2 二維空間中地表橫向沉降曲線

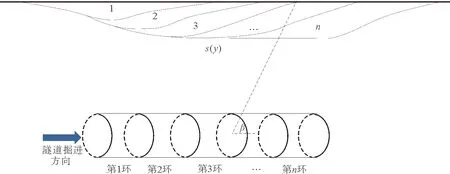
圖3 二維空間中地表縱向沉降曲線

2.2 地表沉降的三維闡述

然而，受隧道施工的擾動，地表點移動軌跡始終指向隧道開挖工作面的中心，其移動矢量在X，Y，Z三個維度上都有分量，如圖4所示，隧道施工結束且地表穩(wěn)定后，在地表形成三維的地表沉降槽，在隧道橫向X、縱向Y和垂直方向Z三個維度上展示著其發(fā)展特征，對于三維空間中的地表沉降則是上述二維空間中地表沉降曲線的“空間組合”，其形狀為中間深，兩側淺的沉降槽，如圖5所示。

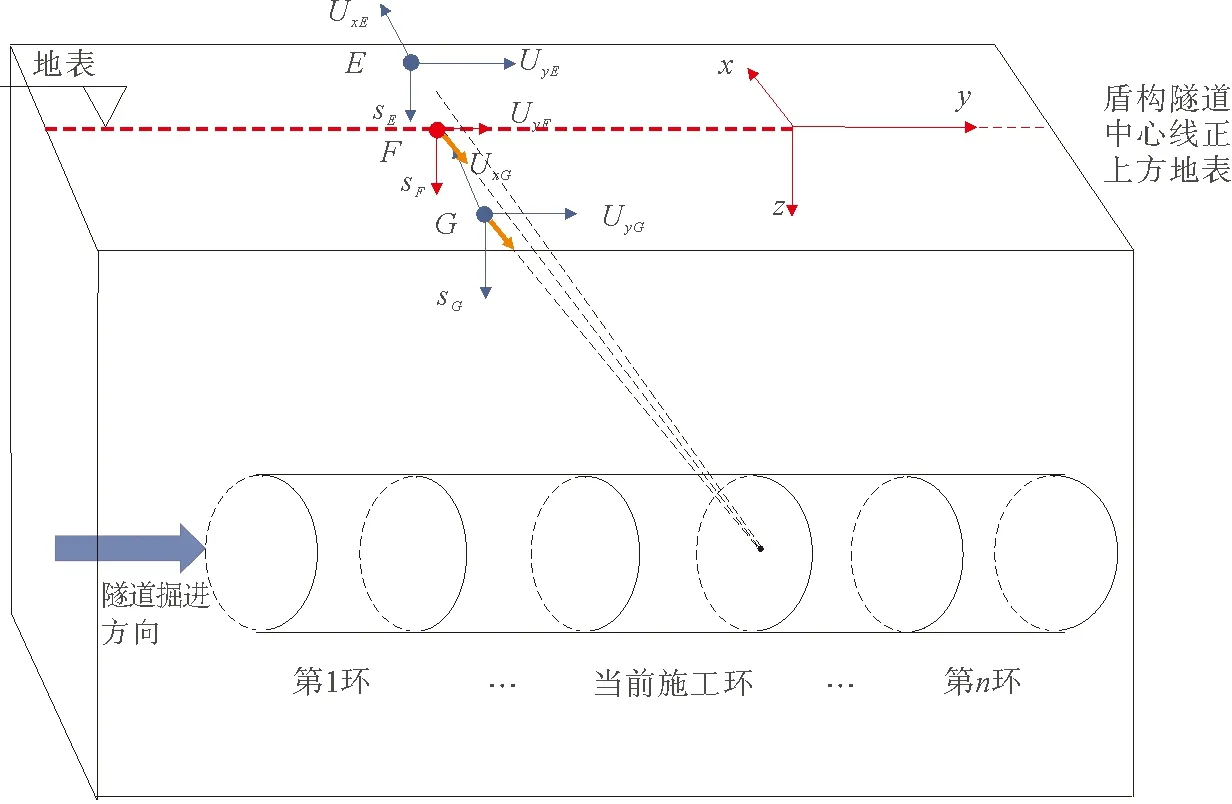
圖4 三維空間下隧道施工地表沉降位移矢量示意

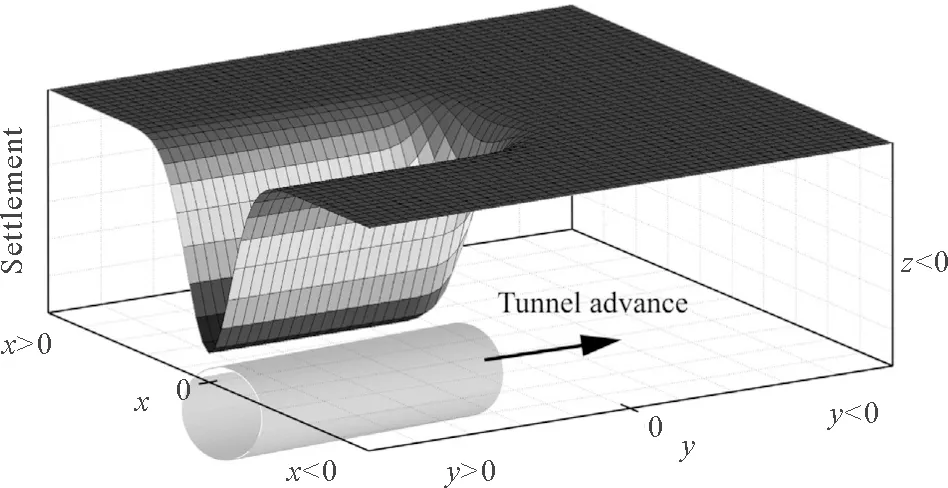
圖5 三維空間中地表沉降槽曲面[15]

2.3 地表沉降的四維闡述

對于盾構隧道施工引起地表沉降問題，盾構機掘進步長(L)是一個重要的影響因素。不難理解，隨著盾構機的向前推進，上述三維的地表沉降槽不斷演化并向前擴展，在三維空間中引入第四個維度，即盾構機掘進步長軸，研究三維沉降槽在步長軸(L)上的展布特征和發(fā)育規(guī)律，即地表沉降的“四維”效應，如圖5所示。

對于地表沉降槽隨盾構機掘進步長演化的證據(jù)還可以由地表上任意一點的移動軌跡來說明。選沿隧道中心線縱剖面上地表上A點，其位移矢量軌跡始終指向隧道掘進工作面的中心，緊隨盾構推進步長(盾構環(huán)數(shù))而發(fā)展演化，如圖6所示。地表沉降槽隨盾構推進步長發(fā)展演化恰是受擾動所有地表點隨盾構推進步長演化的群體效應。

圖6 地表沉降條件和隧道中心線縱剖面上地表任意一點的移動路徑[14]

2.4 地表沉降“五維”空間中“時間軸”詮釋

ALBERT在1905年研究狹義相對論時，提出了“時間和空間的相對性”“四維時空”“彎曲空間”等全新的概念。將時間和空間結合在一起，盾構隧道施工引起地表沉降“五維”空間中的時間軸詮釋也是以此為基礎。

地表沉降槽不僅隨著盾構機的向前推進而不斷向前擴展，而且其數(shù)值還會隨著時間(T)的推移而不斷發(fā)展增大，直至增大到隧道施工特定條件下(地質條件、隧道埋深、隧道尺寸、隧道施工工藝過程)的最大值。

事實上，盾構隧道施工引起的地表沉降取決于2個條件，一是隧道施工在地層中形成的臨空體，二是隧道上覆巖土層的重力，隧道施工在地層中形成臨空體后，上覆巖土層就會在重力作用下向著臨空體中心產生移動，發(fā)展到地表即為地表沉降，這是一個臨空體積不斷向上傳遞的時間過程，即本文將其視為的第五個維度——時間軸(T)。

在實際工程中，盾構機掘進步長是由推進環(huán)數(shù)來計量的，也即每環(huán)管片的長度，我國隧道管片的長度一般有1.0，1.2，1.5 m 3個尺寸，盾構機每當掘進一環(huán)，便停機安裝管片，此時隧道停止掘進，停機時間為1 h左右，即使在停機狀態(tài)，地表點的沉降仍然隨著巖土層中的臨空體積向上傳遞、運動擴散[16]，巖土層固結不斷地發(fā)生著，其時間效應仍然存在，也即在推進環(huán)數(shù)維持不變的情況下，地表沉降槽仍然隨著時間的延續(xù)而發(fā)生不斷的演化，所以將時間因素考慮在內綜合研究地表沉降槽的形成發(fā)展過程以及最后的地表沉降槽幾何特征是至關重要的。

綜上所述，地表沉降的“五維”空間效應是指在地表沉降槽的三維幾何特征(X，Y，Z)表述的基礎上，地表沉降槽在步長軸(L)和時間軸(T)上的演化過程。

因此，將盾構機掘進步長和時間作為兩個維度，研究地表沉降槽的演化規(guī)律更為合理，如圖7所示。

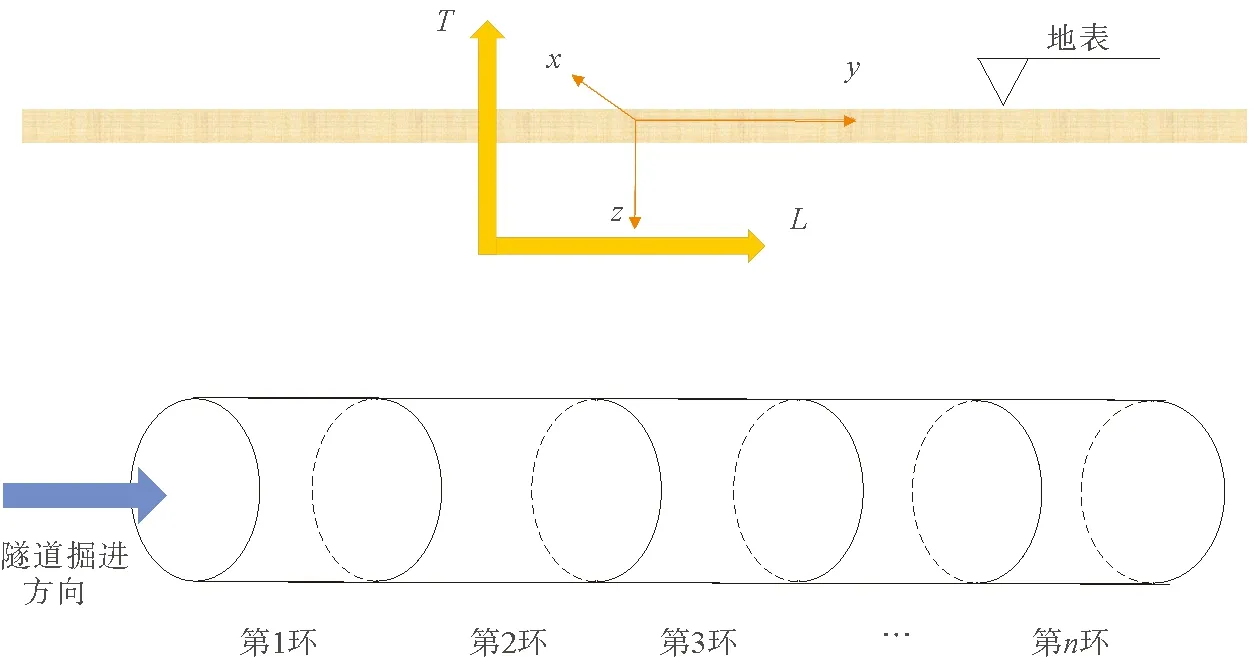
圖7 五維空間下隧道沉降模型坐標系示意

3 各維空間中地表沉降的特征表征

3.1 二維空間中(橫縱剖面)地表沉降幾何特征

二維空間中，地表沉降通過曲線的形式進行展現(xiàn)，故將地表沉降在二維空間中的表現(xiàn)形式定義為“沉降線”，依據(jù)概率積分法的幾何特征點與特征參數(shù)，如圖2所示：

1) 最大下沉點O。最大下沉點為地表沉降曲線上最大下沉值的點，對于單洞隧道施工來講，一般位于隧道開挖斷面的正上方。

2) 沉降邊界點A，B。盾構隧道施工對地表產生的影響是從隧道中心處向兩側逐漸遞減的。盾構隧道施工對地表不再產生擾動的最近點，即為沉降的邊界點。

3) 拐點C，D。拐點是指沉降曲線凹凸的分界點，其位置一般在隧道圍巖明顯變形區(qū)域的外邊緣的正上方，拐點C，D處的地表下沉值一般是地表最大下沉值的一半。

4) 隧道施工影響范圍。地表沉降兩側邊界點內的區(qū)域即為隧道施工對地表的影響范圍。隧道開挖的影響范圍與巖層狀態(tài)相關，一般用主要影響角正切值來反應。

5) 主要影響角α。沉降曲線外邊緣至隧道開挖斷面最外輪廓線底部連線與水平線的夾角稱為主要影響角，如圖2中角α。

6) 超前影響角β。盾構工作面前方地表開始移動的點與工作面的線連，此連線與盾構推進方向的夾角稱為超前影響角，如圖3中角β。

3.2 三、四、五維空間中地表沉降幾何特性

在三維空間中，地表沉降最終形態(tài)是一個“中間深，兩側淺”的沉降槽。

在四維空間中，地表沉降具有了隨著步長演化的特征，即不僅是地表沉降槽本身的幾何特征，地表沉降槽還隨著步長的逐漸推進而不斷發(fā)展演化。因此，將地表沉降在“四維”空間下的表現(xiàn)形式定義為“沉降超體”，其幾何意義為：將地表沉降槽三維圖形抽象為一個點(可視為點)，該點沿步長軸而發(fā)展演化，表現(xiàn)為“步長-沉降點”的矢量效應。

在四維空間的基礎上引入時間變量，不僅能夠認識地表沉降槽隨盾構施工步長的演化規(guī)律，也能得到沉降槽在隨步長演化的基礎上進一步隨著時間的演化規(guī)律，即在時間軸上的生長規(guī)律，將地表沉降在“五維”空間中的表現(xiàn)形式定義為“沉降卷超體” ，其幾何意義為：將地表沉降超體“步長-沉降點”矢量效應抽象為一個點，視該 “點”在沿時間軸發(fā)展演化，表現(xiàn)為“時間-步長沉降點”矢量效應。盾構隧道施工引起地表沉降的“沉降超體”“沉降卷超體”等概念的提出，為研究地表沉降的“五維”空間效應提供了新的思路。各維度地表沉降幾何特征及屬性如表1所示。

表1 地表沉降各維度空間下幾何特征、演化規(guī)律比較

4 沉降“五維”空間效應工程驗證

深圳市城市軌道交通13號線三工區(qū)留仙洞站—白芒站區(qū)間工程全長4.4 km，盾構機施工過程中地表沉降，現(xiàn)場布設大量地表沉降監(jiān)測點，用以觀測地表實時沉降數(shù)據(jù)，討論并驗證地表沉降的“五維”空間效應，取監(jiān)測點1—4說明本文的沉降時間效應，監(jiān)測點的布置如圖8所示。

圖8 留仙洞站—白芒站區(qū)間部分地表沉降測點示意

在深圳城市軌道交通13號線的現(xiàn)場施工過程中，留仙洞站至白芒站區(qū)間8月11日至8月13日因現(xiàn)場施工原因并未進行推進。左線盾構隧道滯留于225環(huán)，右線盾構隧道滯留于159環(huán)。3 d內地表沉降情況(圖9)能夠準確地反應地表沉降的時間效應問題。

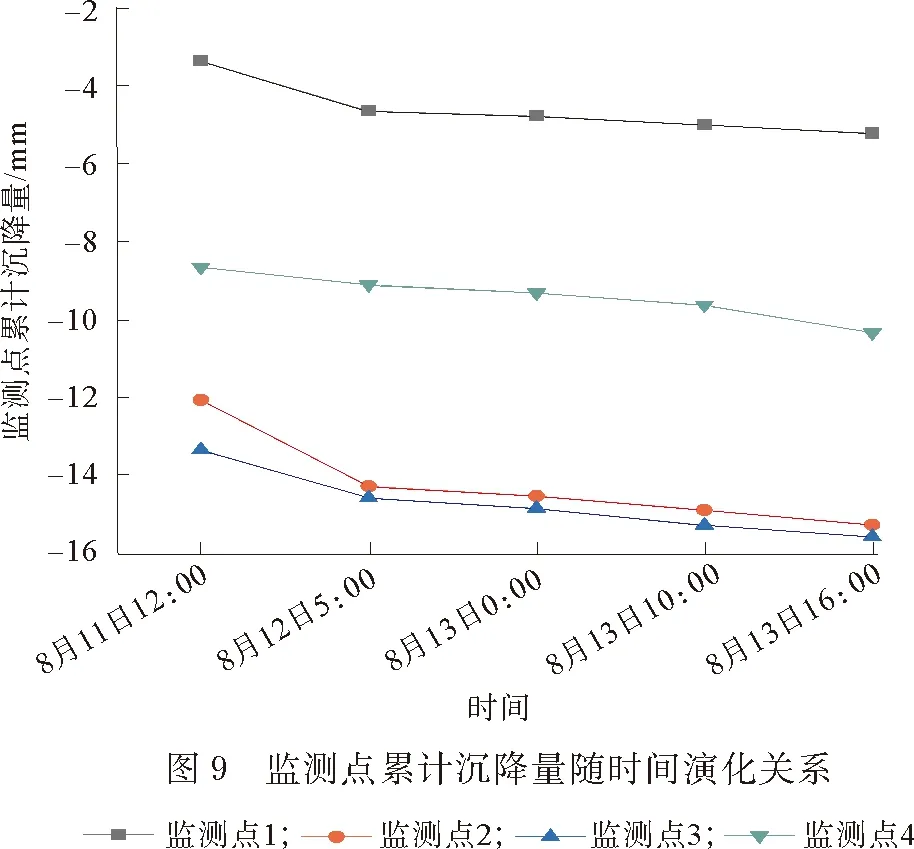
如圖9所示，地表沉降的發(fā)展過程具有明顯的時間效應。在左右線隧道盾構機停機狀態(tài)下，監(jiān)測點1—4均發(fā)生單獨于時間坐標軸上的沉降現(xiàn)象，即地表的沉降過程在不受盾構機推進擾動的情況下，僅隨時間的發(fā)展而發(fā)生沉降。位于隧道中心線上的監(jiān)測點2和監(jiān)測點3的地表沉降量較大，而對于偏離隧道中心線上的監(jiān)測點1所觀測到的地表沉降量較小(符合地表沉降的三維空間分布形態(tài))。在盾構機尚未推進至260環(huán)時，監(jiān)測點4因超前影響的原因，也發(fā)生了隨時間的沉降。

觀測左線盾構機從201環(huán)推進至222環(huán)，監(jiān)測點2(位于212環(huán))的整個沉降過程。監(jiān)測點2位于觀測區(qū)間的中間位置，能夠準確反映盾構機未到時、下穿時、穿過時整個周期的地表沉降隨盾構機推進步長的演化規(guī)律，如圖10、圖11所示。

由圖10可以發(fā)現(xiàn)，地表的沉降數(shù)據(jù)隨步長有明顯的變化，沉降的步長效應顯而易見。在盾構機離監(jiān)測點2較遠時，監(jiān)測點2因超前影響的原因，發(fā)生地表沉降，當盾構機離監(jiān)測點距離較近時，在盾構機的推力作用下，反而使監(jiān)測點2出現(xiàn)隆起，當盾構機推過監(jiān)測點2時，地表繼續(xù)沉降。在圖11中可以直觀地看出不同環(huán)區(qū)間地表沉降和隆起現(xiàn)象，且發(fā)現(xiàn)在盾構機靠近監(jiān)測點時，地表的變形速率最大，離監(jiān)測點較遠時沉降速率較慢。

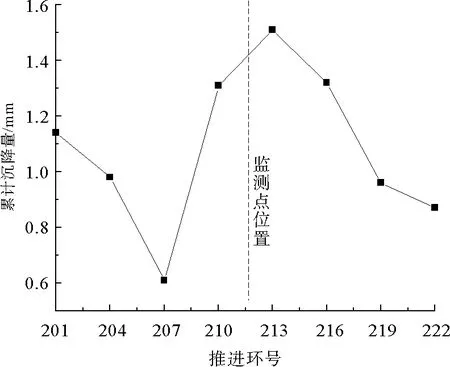
圖10 監(jiān)測點2累計沉降量隨盾構機推進環(huán)數(shù)演化關系

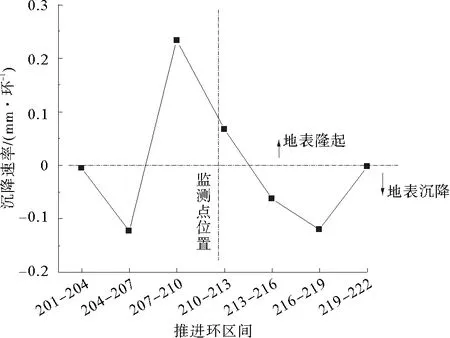
圖11 監(jiān)測點2沉降速率隨盾構機推進環(huán)數(shù)關系

綜上，由深圳市城市軌道交通13號線具體監(jiān)測數(shù)據(jù)可以得出，地表沉降的發(fā)展規(guī)律具有明顯的時間效應，地表三維沉降槽不但具有步長軸上獨立的演化規(guī)律，而且也存在時間軸上獨立的演化規(guī)律，因此地表沉降具有典型的“五維”空間效應得以證實。

5 盾構隧道施工引起地表沉降的“五維”研究展望

盾構隧道施工引起地表沉降“五維”空間效應是個全新的理念，仍有諸多問題需要進一步研究：

1) 在盾構隧道施工引起地表沉降的力學根源上，巖土體的自重可謂是“力源”，盾構隧道施工引起上覆巖土體的自重應力重新分布，在這個過程中巖土體將產生變形，這種變形是地表產生沉降的根源。因此，如何在五維空間中認識隧道上覆巖土體應力重新分布的狀態(tài)，并研究其變形規(guī)律，建立基于五維空間的隧道施工引起地表沉降的力學模型，乃是今后該專題研究的首要任務。

2) 在盾構隧道施工引起地表沉降數(shù)學計算模型建立上，盾構隧道施工在地下產生“臨空體”，臨空體向上發(fā)展的過程恰是被擾動的巖土體中空隙演化過程，可謂是“空隙元”，研究盾構隧道施工造成巖土體空隙元在五維空間中的擴散規(guī)律，并用微分方程加以描述，從而建立地表沉降的數(shù)學表達式，對地表沉降的“五維”效應進行數(shù)學計算。因此建立基于“五維”空間的盾構隧道施工引起地表沉降計算模型，也是該專題進一步研究的方向之一。

3) 在工程中，具體研究地表沉降的“五維”空間效應與地質條件參數(shù)、隧道幾何參數(shù)、隧道掘進參數(shù)等的具體關系，進一步驗證基于“五維”空間的盾構隧道施工引起地表沉降計算模型，并在現(xiàn)場實施可靠的監(jiān)測予以驗證，同時編制基于“五維”空間的盾構隧道施工引起地表沉降預計方法，以求更加深入認識和研究盾構隧道施工引起地表沉降的復雜性和真實過程，并能對工程中的地表沉降現(xiàn)象進行精準(空間上、時間上)的預測。

4) 在盾構隧道施工引起地表沉降多維空間的表示方法上，將張量分析、畫法幾何等應用于隧道施工引起地表沉降的五維空間效應研究中。地表點的位移是一個時刻指向隧道開挖工作面的“位移矢量”，由單個點的位移矢量到多個點位移矢量組成的三維沉降槽、再到四維的“沉降超體”、五維的“沉降卷超體”，實則是矢量圖形的變化過程，用恰當?shù)臄?shù)學手段和數(shù)學工具進行科學描繪，不僅對理解地表沉降多維演化規(guī)律具有重要作用，還會有助于理解地表沉降“五維”空間效應的物理機制，在后續(xù)研究中可以通過空間矢量運算或張量分析等數(shù)學工具，研究沉降槽的“五維”空間效應。

5) 在盾構隧道施工引起地表沉降五維空間的研究技巧上，“降維”的思想方法是研究高維空間的有力手段。對于地表沉降槽的“五維”空間效應研究，運用“降維”的手段可以使復雜多維度的地表沉降演化問題分析更加方便、直觀。任何一級低維度空間都是高一級維度空間的橫截面，并以高一級維度空間以多出的維度為軸線移動而形成的空間，例如二維空間下的地表沉降線就是三維空間下的地表沉降槽的剖面線，對于“四維”空間下的地表沉降超體，具體來說即是研究三維的沉降槽在步長軸的獨立變形規(guī)律，同理類比至“五維”空間，將“五維”空間沉降卷超體降維即為沉降超體(三維沉降槽+步長)，研究沉降超體在時間軸上的獨立變形規(guī)律，即可得到地表沉降的“五維”空間效應。因此，在研究盾構隧道施工引起地表沉降“五維”空間效應時，也可以借用“降維”分析的思想方法，這種“降維”的思想可以使得我們在研究高維問題時尋找到有力的突破點。如圖12所示，為地表沉降“五維”空間效應的研究方法。

圖12 地表沉降“高維空間”研究方法

6) 與隧道施工引起地表沉降已有經驗公式的銜接上，Peck公式、隨機介質理論(概率積分方法)在五維空間中的發(fā)展；

7) 在實驗室研究方面，構建“五維”空間的盾構隧道施工引起地表沉降相似材料模擬實驗模型，并進行相應的科學試驗驗證；

8) 在盾構隧道施工引起地表沉降的多維性研究上，隨著人們對科學真諦的追求，對自然或科學中分維、多維的研究興趣越來越濃厚，堅信盾構隧道施工引起地表沉降的多維性，包括地表沉降的“分維性”“五維效應”是真實存在的，那么如何在更精細的維度(分維)和更高級的維度(五維)上研究地鐵隧道施工引起地表沉降的特征和規(guī)律，進而在多維度空間建立地鐵隧道施工引起地表沉降的“空間-步長-時間演化理論”，乃是該專題今后研究的重要任務。

6 結束語

本文通過對盾構隧道施工引起地表沉降多維性的探索和深圳軌道交通13號線的長期跟蹤監(jiān)測，研究分析了三維地表沉降槽在步長軸和時間軸上的獨立演化特征和規(guī)律，證明了盾構隧道施工引起地表沉降“五維”空間效應的客觀存在性，盾構隧道施工引起的地表沉降具有典型的“五維”空間效應，具體表現(xiàn)為：“三維沉降槽”具有在步長軸上獨立的演化的特征，即“三維沉降槽”隨步長的推進而發(fā)生演化，形成“沉降超體”；而“沉降超體”又在時間軸上獨立演化，隨時間的增長而發(fā)生演化，即形成“沉降卷超體”。

然而，盾構隧道施工引起地表沉降“五維”空間效應是個全新的理念，仍有盾構隧道施工引起地表沉降“五維”空間效應的表示方法、力學機理、計算模型、預計方法等諸多問題需要進一步研究，本文只是拋磚引玉，今后將結合地鐵隧道建設項目具體實踐進行更加深入的研究。

致謝：感謝導師謝和平院士、張玉卓院士、Marek. KWASNIEWSKI教授、楊倫教授在學術思想上給予啟迪，感謝M. D. KOVALENKO教授和I. V. MENSHOVA研究員給予該問題研究的力學和數(shù)學啟發(fā)，張春會教授及李剛、李冉、張永義、朱向飛、張琳、師啟蒙等同學多次參加研討和搜集資料，在此一并表示感謝。