雙有源全橋DC-DC變換器的電流應力優化控制

曾寶寶，袁旭峰，鐘九牧，劉偉豐，張 港

（貴州大學 電氣工程學院，貴州 貴陽 550025）

0 引言

新能源高效利用已成為時代發展主題[1]。雖然以太陽能、風能為代表的新能源發電具有清潔、安全和可持續的優點，但其同時也存在能量波動性、間歇性的缺點，存在發電出力受環境影響較大、導致系統與負荷之間出現供需不平衡以及母線電壓穩定性較差的問題[2]。目前看來，儲能技術是解決該問題的有效辦法之一。儲能單元可較好地實現“削峰填谷”、抑制系統功率波動、穩定直流母線電壓等功能[3,4]。由于需要實現功率雙向流動、高低壓隔離等功能，因此，隔離型雙向DC-DC變換器成為儲能系統的核心環節[5,6]。

由于雙有源全橋（dual active bridge，DAB）DC-DC變換器具有能量雙向流動、功率密度高、高低壓側電氣隔離、較易實現軟開關等優點而被廣泛應用于交直流混合微電網、儲能系統、電動汽車等場合的能源變換系統[7-10]。

DAB變換器通常工作在移相控制方式下：在原副邊全橋以及各全橋內施加不同的觸發脈沖，在高頻變壓器一、二次側生成一定相移量的方波電壓，通過調節方波電壓之間的移相角來控制傳輸功率的大小及方向[11]。利用各移相角的最優組合，可以實現DAB的快速響應、傳輸功率、電流應力以及回流功率控制優化[12]。由于單移相控制的限制較大，雙重移相控制（dual-phase-shift control，DPS）、擴展移相控制（extend-phase-shift control，EPS）以及三重移相控制（triple-phase-shift control，TPS）等控制方法相繼被提出[13,14]。文獻[15]提出了虛擬直接功率控制的方法。該方法顯著提升了變換器在輸入電壓突變、負載突變等情況下的動態響應性能。文獻[16]提出了負載電流前饋的控制方法：在保證變換器動態性能的前提下，算法的運算量更小，可移植性高。文獻[17]在拓展移相控制方式下，提出了環內直接功率優化的方案：與最小電流應力控制相結合，提升變換器的穩態及動態性能，減小電流應力。文獻[18]詳細分析了在不同移相控制策略下 DAB變換器的最小電流應力特性，結果表明：在TPS控制下，變換器具有更小的電流應力，可全功率范圍實現開關管的軟開關，傳輸效率更高。文獻[19]利用二維遍歷算法，引入效率優化權重，構建了電流應力和傳輸效率的綜合優化目標；在不提高DAB電流應力的同時，有效提高了傳輸效率。

為提高變換器的動態性能以及傳輸效率，本文提出一種基于三重移相控制、結合模型預測及負載電流前饋控制、優化電流應力的方法：通過karush-kuhn-tucker（KKT）算法得到不同功率區間下DAB最小電流應力內外移相角組合；同時，內移相角經負載電流前饋控制優化，外移相角經輸出電壓預測模型優化，使得電流應力減小、變換器的動態響應能力顯著提高。最后，在仿真模型下，與傳統模型預測控制及電流應力優化控制進行對比，驗證了在輸入電壓突降、負載突增等工況下，該優化方案的正確性及有效性。

1 TPS控制下DAB工作特性

如圖1所示，DAB變換器等效拓撲由2個對稱的H橋、高頻隔離變壓器、等效漏感L以及輸入、輸出側電容 C1和 C2組成。其中，uab和 ucd為高頻腔內輸入、輸出方波電壓，i1和iC1分別為一次側輸入電流和輸入電容電流，i2和iC2分別為二次側輸出電流和輸出電容電流，高頻變壓器變比為n:1，R為等效負載電阻。DAB變換器功率的傳輸方向可以通過調節一次側方波電壓 uab和二次側方波電壓ucd之間的相移量來實現。通常，功率由相位角超前側流向滯后側，而變換器傳輸功率的大小則由uab和ucd的幅值和相位差決定。為討論方便，本文假設功率由uab流向ucd，變壓器變比n=1，電壓傳輸比k=U1/nU2，并規定k>1。

圖1 雙有源全橋雙向DC-DC變換器拓撲Fig. 1 Topology of dual active full-bridge bidirectional DC-DC converter

TPS控制下，D1為原邊H橋內移相角，即開關管S1超前S4的相移量占比；D2為橋間移相角，即開關管 S1超前 S5的相移量占比。應注意，D3定義為S1超前S8的相移量占比。當變換器工作在0≤D1≤D2≤D3≤1 及 0≤D2≤D1≤D3≤1 這 2 種工作模式下，剛好能實現全功率范圍的電流應力優化[18]。DAB變換器開關管觸發脈沖、電感電壓uL、電感電流iL波形如圖2所示。圖2中，Ts=1/(2fs)，fs為 DAB變化器開關頻率，t12和 t56為電感電流iL過零點。

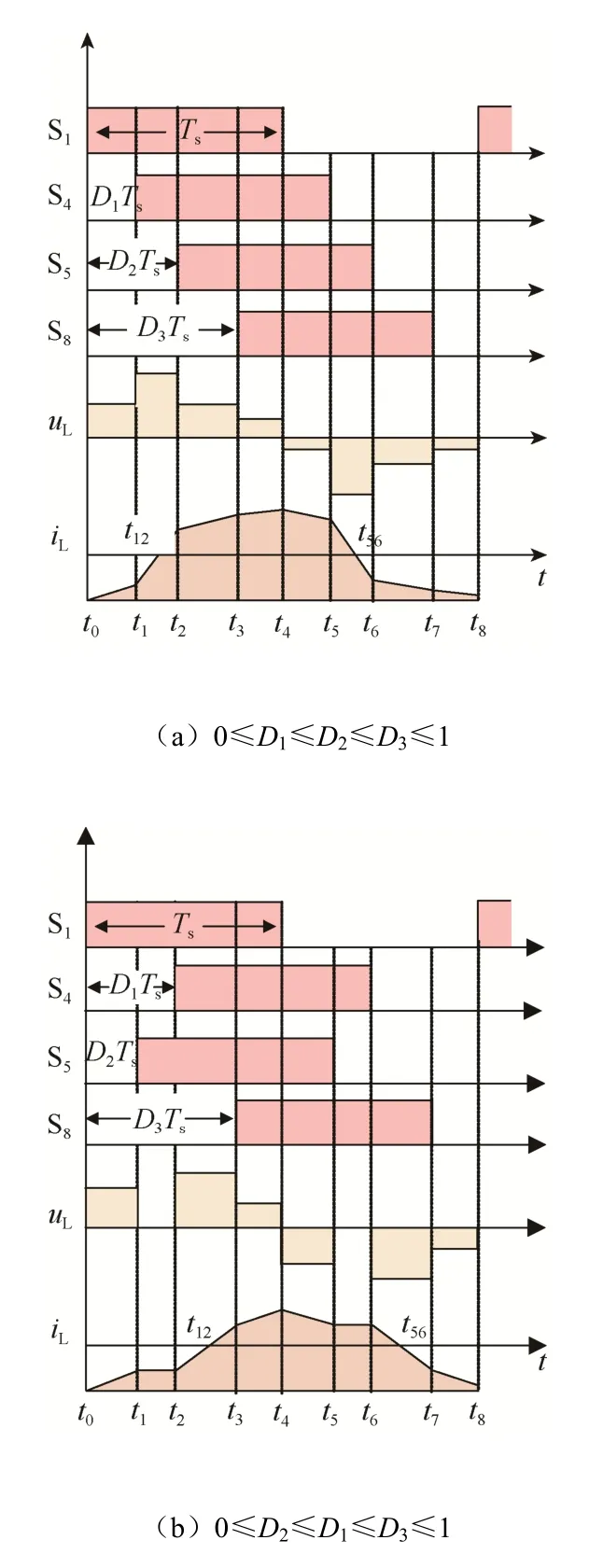
圖2 TPS控制下DAB變換器電壓電流波形Fig. 2 Voltage and current waveforms of DAB converter under TPS control

圖2（a）中，設 t0=0，則 t1=D1Ts，t2=D2Ts，t3=D3Ts，t1=Ts，t5=(1+D1)Ts，t6=(1+D2)Ts，t7=(1+D3)Ts，t8=2Ts。由于 iL(t0)=iL(t4)，可求得 0≤D1≤D2≤D3≤1模式下各時刻電感電流值為：

2 基于負載電流前饋控制的電流應力優化

通過此前分析可知，DAB傳輸功率及電流應力通常為移相比的多元函數。通過尋找移相比的最優組合，能得到較好的傳輸效率。在傳統控制策略中，通常由PI反饋得到變換器移相比，這極大降低了變換器的動態性能。本文擬基于TPS控制，先由負載電流前饋結合電流應力優化得到內移相比D1和D3，再由模型預測控制得到外移相比D2，在減小電流應力的同時，保證變換器的動態性能。

TPS控制下的傳輸功率及電流應力為D1，D2，D3的函數，可通過KKT算法尋找使得電流應力最小的移相比組合[17]。該方法的具體數學形式為：

式中：Y為優化目標函數；x為自變量；hi(i=1,2,···)為等式約束條件；gi(i=1,2,···)為不等式約束條件。文獻[20]施加傳輸功率、軟開關等等式及不等式約束條件，得到0≤D1≤D2≤D3≤1模式下最小電流應力內移相角D1和D3表達式為：

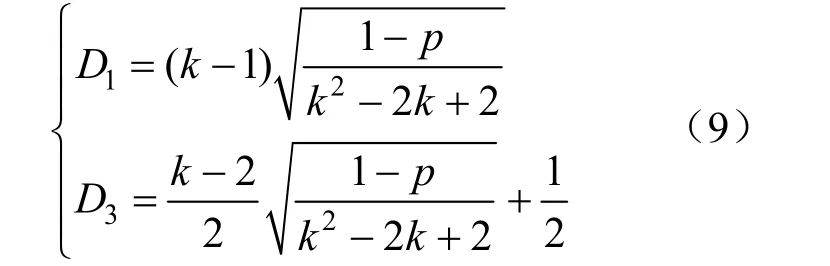
此時對應的功率區間為：(2k–1)/k2≤p≤1。在0≤D2≤D1≤D3≤1模式下，最小電流應力內移相角D1和D3表達式為：

此時對應的功率區間為：0≤p<(2k–1)/k2。

為穩定輸出電壓，引入負載電流前饋控制[16]，其結構示意如圖3所示。

圖3 負載電流前饋控制結構示意圖Fig. 3 Schematic diagram of load current feedforward control structure

由圖3知，輸出電壓參考值Uref與實時采集的輸出電壓U2作差后經過PI控制器（P=50，I=500）得到虛擬輸出電壓參考值；輸出電流參考值則由Uref、U2、i2得到，用Pm替換移相比中的標幺傳輸功率p。優化后的移相比如表1所示。

表1 負載電流前饋控制下電流應力優化移相比Tab. 1 Current stress optimization shift comparison under load current feedforward control

3 基于模型預測控制的動態響應優化

3.1 輸出電壓預測模型的建立

由圖1可知，TPS控制下DAB變換器的電路微分方程可表示為：

由于電感電流在一個周期內具有對稱性，根據式（4）（5）（11），結合圖 2，可分別求得TPS控制下DAB變換器處于0≤D1≤D2≤D3≤1和 0≤D2≤D1≤D3≤1模式的輸出電壓狀態空間平均方程：

對式（12）的輸出電壓微分項進行前向歐拉離散化處理，即：

可得：

3.2 外移相比的計算

為了穩定輸出電壓，在式（18）中增加由輸出參考電壓Uref與實時輸出電壓U2(k)的差值經PI調節得到的反饋調節電壓ΔU2。結合第2節分析得到的內移相比D1和D3，優化策略控制下移相比組合可歸納如表 2所示。系統控制結構圖如圖 4所示。

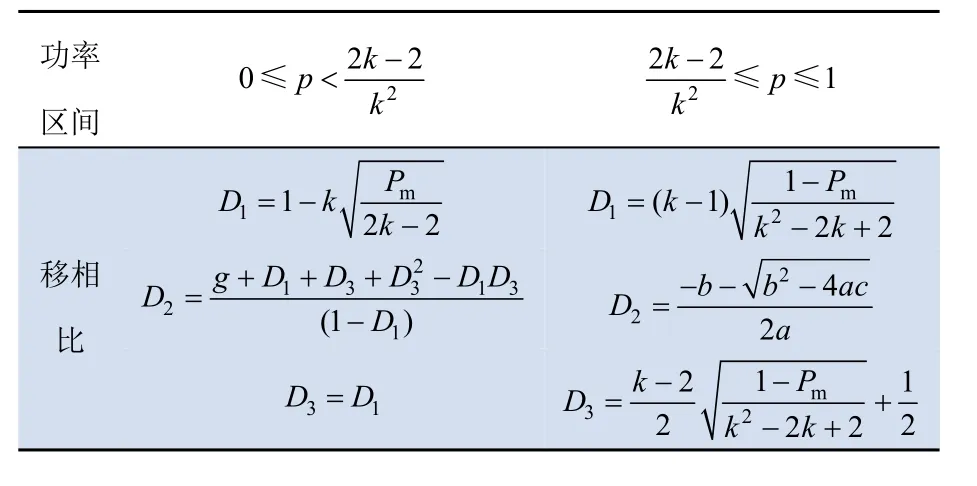
表2 優化策略控制下移相比表達式Tab. 2 Shift comparison expression under optimized strategy control

圖4 優化控制策略下系統控制結構Fig. 4 System control structure under optimized control strategy

4 仿真結果及分析

為進一步驗證理論分析的正確性與可行性，在 MATLAB/SIMULINK中搭建了仿真模型，模型參數如表3所示。

表3 SIMULINK仿真模型參數Tab. 3 Simulation model parameters of SIMULINK

4.1 輸入電壓突降下的動態性能

輸出電壓為30 V，負載電阻為30 Ω；在0.05 s時，輸入電壓由100 V跳變至70 V。圖5所示為傳統電流應力控制及優化策略控制下的輸出電壓、電流波形。由圖5可知，傳統電流應力控制下，電壓恢復時間約為30 ms且具有一定超調量；在優化策略控制下，輸出電壓基本保持不變。

圖5 輸入電壓突降時2種控制策略下的輸出電壓電流波形Fig. 5 The output voltage and current waveforms under two control strategies when the input voltage steps down

4.2 負載突增下的動態性能

電壓輸入為100 V，輸出電壓為30 V；在0.05 s時，負載電阻由30 Ω跳變到15 Ω。由圖6可知，傳統電流應力控制下電壓恢復時間約為20 ms，優化策略控制下輸出電壓基本保持穩定，動態響應時間可以忽略。

圖6 負載突增時2種控制策略下的輸出電壓電流波形Fig. 6 The output voltage and current waveforms under the two control strategies when load steps up

4.3 輸入電壓突降下的電感電流應力

輸出電壓為30 V，負載電阻為30 Ω；在0.05 s時，輸入電壓由100 V突降至70 V。圖7所示為傳統模型預測控制及優化策略控制下電感電流波形圖。由圖7可知，在傳統模型預測控制下，雖然動態性得到提升，但電感電流應力較大，在0.05 s時由17.6 A降低至11.2 A；在優化策略控制下，電感電流應力得到優化，由8.5 A降至6.1 A。

圖7 輸入電壓突降時2種控制策略下的電感電流波形Fig. 7 Inductor current waveforms under two control strategies when the input voltage steps down

4.4 負載突變下的電感電流應力

輸入電壓為100 V，輸出電壓為30 V；0.05 s時負載電阻由30 Ω跳變到15 Ω。圖8顯示了傳統模型預測控制及優化策略控制下電感電流波形。由圖8可知，在傳統模型預測控制下，電感電流由15.1 A提升至16.2 A；優化策略控制下，電感電流由9.3 A提升為12 A。

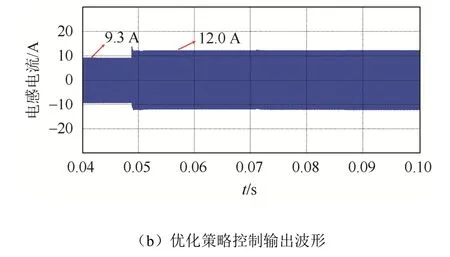
圖8 負載突增時2種控制策略下的電感電流波形Fig. 8 Inductor current waveforms under two control strategies when the load steps up

5 結論

針對DAB電流應力及動態性能問題，提出了一種模型預測及負載電流前饋控制的方法。仿真結果表明，與傳統電流應力優化控制策略相比，該方法提高了 DAB在輸入電壓突降及負載突增時的動態性能，輸出電壓基本保持不變，變換器的電流應力得到優化。