地震強度指標選擇對長周期鋼結構余震IDA分析的影響

王海東，張寅科

（1.湖南大學建筑安全與節能教育部重點實驗室，湖南 長沙 410082；2.湖南大學土木工程學院，湖南 長沙 410082）

引言

我國大陸的淺源地震可以分為三種基本類型，分別為主震型、震群型和孤立型，根據歷史震害資料，截止1987年為止，主震型和震群型地震共占88%，沒有強余震的孤立型地震僅占12%，當初期強余震的震級與主震接近時，地震烈度與主震相比增加半度及Ⅰ度［1－2］。近些年發生的集集地震和汶川地震在主震后也都伴隨發生多次強余震。而現有的國內外規范中都未將余震考慮到結構設計當中，結構設計可能偏向不安全。

國內外學者對結構在主余震作用下的定量分析方法進行了充分研究。張沛州等［3］提出了新的主余震序列分析結構抗震性能計算方法-MASA，分別運用到單自由度體系和不同延性的鋼筋混凝土框架結構，分析結果表明：余震顯著影響鋼筋混凝土框架結構的抗震性能，特別是低延性結構，并且影響程度直接與主震的震級相關；WEN 等［4］以5 層RC 結構為研究對象，提出了在主余震序列下結構易損性分析框架，研究結果表明：基于能量的結構損傷指標能更好地反映余震對結構的附加影響，隨著主震或者余震強度的增大，余震增大結構的損傷，當主震對結構損傷達到30%～60%，余震對結構易損性影響更大；TRAPANI 等［5］采用雙IDA方法分析了含有填充墻的RC 框架結構在主余震用下的易損性，研究結果表明：填充墻能夠顯著減少結構在主震作用下的損傷，同時減少了其在中震下的經濟損失，但要特別注意框架和填充墻之間的附加剪力需求，可能導致結構突然破壞；于曉輝等［6］利用Park-Ang 指數作為結構損傷指標，建立了基于logistic 回歸方法的損傷狀態相關余震易損性分析，并建立余震損傷狀態躍遷概率和余震易損性指數作為余震安全性評估的定量分析指標，研究結果表明：隨著主震損傷的提高，余震發生更嚴重破壞的概率顯著提高。

結構在較大地震作用下，性能會被削弱，產生塑性變形，剛度和強度退化，導致結構的周期延長，高階陣型的影響加強，為了降低結構分析的離散性，從地震強度指標入手，LUCO 等［7］提出了基于位移反應譜的IM1E&2E；KOHRANGI 等［8］建立了一段周期范圍內的加速度反應譜的指數平均數Saavg作為地震動強度（IM）指標；左占宣等［9］考慮結構損傷對自振周期的延長，基于等效單自由度結構周期，提出了等效周期譜加速度Sa（Teq）。并對結構在地震作用下，對地震強度指標的離散性和相關性進行了驗證研究。

現有的主余震分析框架中，都還是采用基于彈性周期的地震動強度指標，對于主震損傷結構可能不適用，并且各種改進IM指標的提出和驗證都是基于一次地震動，而對主震損傷結構在余震作用下的各IM指標的適用性和優劣性研究較少。基于此，本文選取各種改進后的IM 指標，先使得結構在主震作用下達到特定損傷，再進行余震的IDA分析，從離散性和相關性兩個維度進行對比研究，為選出適用于余震分析的IM指標做些基礎工作。

1 IM指標

峰值加速度（PGA）是我國抗震規范默認的IM 指標，用于定義地震風險和地震動強度的調幅參數；一階陣型譜加速度Sa（T1）是具有結構特性的IM 指標，用于歐美規范的地震風險定義和調幅參數，這兩個參數在結構抗震分析中得到了最為廣泛的應用。然而對于高聳的長周期結構、進入彈塑性階段的延性結構和受高階陣型影響的結構，PGA和Sa（T1）并不適用。國內外學者基于此，提出了各種改進后的IM指標。

1.1 基于加速度譜的IM指標

CHOPRA 等［10］基于割線剛度提出等效周期Teq代替一階振型周期T1，考慮了周期延長，一定程度上反映結構進入彈塑性的動力特性，Teq的計算公式為：

式中：μ為延性系數；α為雙線性本構關系中屈服后的切線剛度和初始剛度的比值。通過對結構進行poshover推覆得到能力曲線并根據FEMA-356［11］的方法理想化成雙折線曲線，求得μ和α分別為2.13和0.109。

CORDOVA 等［12］提出了考慮周期延長的地震動強度調幅參數，該公式同時反映了譜加速度和反應譜的形狀，計算公式為：

式中：參數a和c分別確定為0.5和2。

HASELTON 等［13］研究發現在倒塌分析中，大于一階陣型周期的周期所對應的加速度反應譜是更合適的IM指標，從而提出了以下公式：

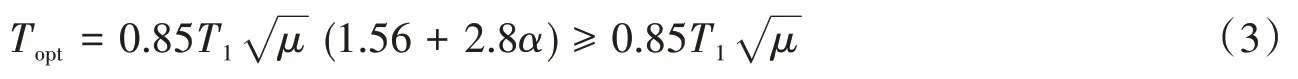
式中：參數μ和α和式（1）相同。

BOJORQUEZ等［14］基于一段周期范圍的加速度反應譜的幾何平均數，提出了新的IM指標，計算公式如下：

Np公式如下：

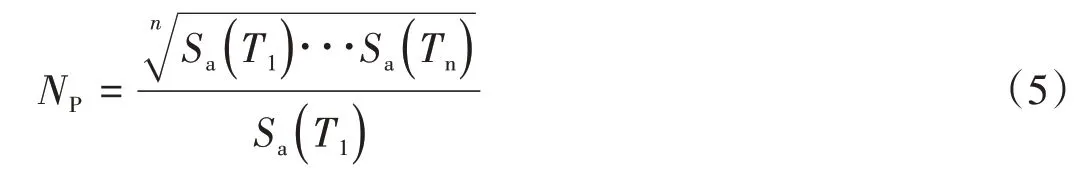
式中：Tn=2T1，α=0.4，周期間隔取0.2 s。

KOHRANGI等［15］提出了一段周期范圍內對數平均加速度反應譜Saavg，計算公式如下：

式中：周期段從0.2T1到1.5T1，周期間隔取0.2 s。

1.2 基于速度譜的IM指標

一些學者提出了基于速度反應譜的IM 指標，都是在一段周期范圍內進行速度反應譜的積分，只是系數和積分范圍不同，分別如下：

NAU等［16］提出的計算公式：

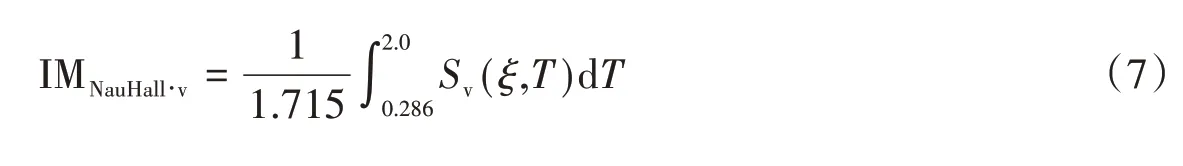
KAPPOS［17］提出的計算公式：

式中：t1=t2=0.2T1。

MATSUMURA［18］提出的計算公式：

式中：Ty為結構pushover曲線中的彈性周期。

1.3 基于位移譜的IM指標

LUCO等［7］既考慮了高階陣型的參與和結構非線性的影響，提出了基于位移譜的IM指標，計算公式如下：

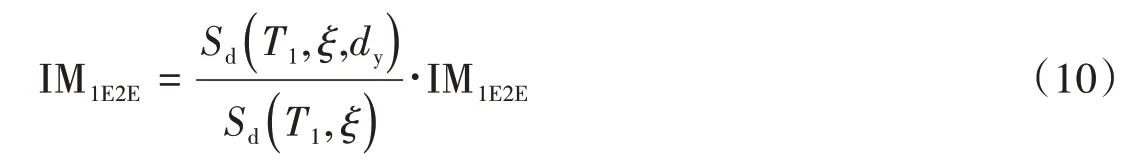
式中：IM1E2E的計算公式如下：

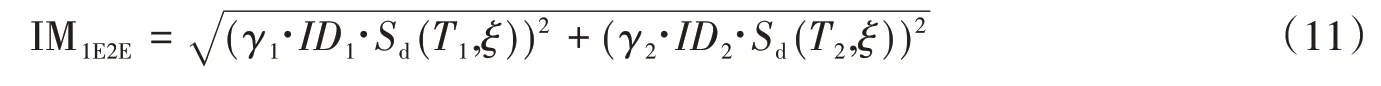
式中：各個參數詳見文獻［7］。

2 地震動記錄選擇

本文基于美國太平洋地震工程研究中心PEER（Pacific Earthquake Engineering Research）NGA-West2 強數據庫，選取20 條集集地震的主余震序列。挑選原則如下：（1）所選取的主余震地震動的矩震級Mw≥5.0；（2）多條余震中選取水平幾何平均峰值速度最大的余震；（3）水平幾何平均峰值加速度PGA≥0.05 g；（4）水平幾何平均峰值速度PGV≥3 cm/s；（5）根據SHREY 等［19］方法剔除近場脈沖地震動；（6）選取C 類場地，平均剪切波速Vs30在360～760 m/s。主余震序列的信息見表1

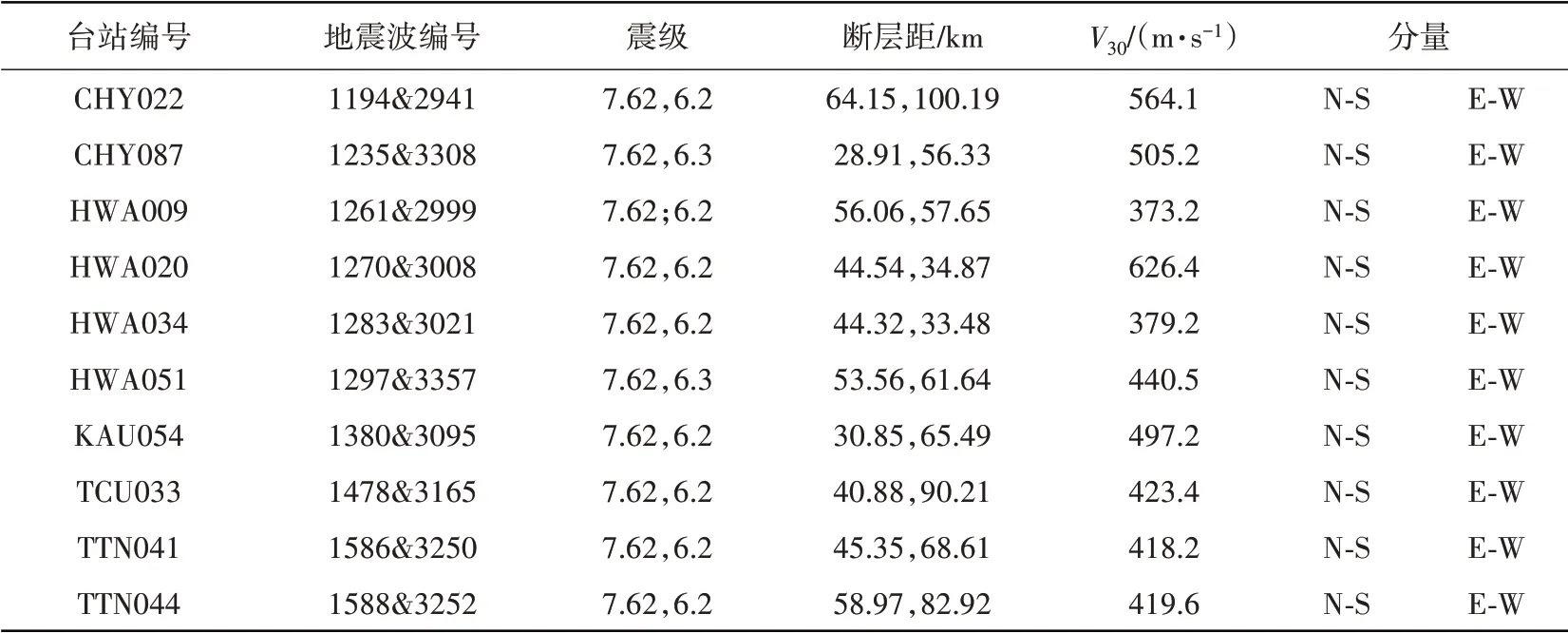
表1 選用的主余震序列信息Table 1 Summary of the selected mainshock-aftershock sequence

圖1給出了主震和余震的標準譜。由圖可見：在小于0.5 s時，主震與余震的標準譜接近，周期大于0.5 s后，主震的標準譜大于余震。

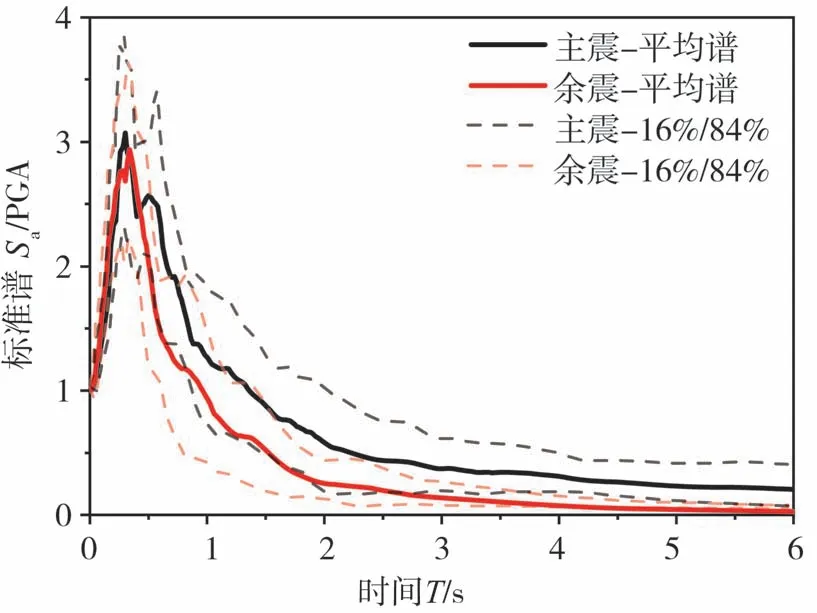
圖1 主余震序列的標準譜Fig.1 Normalized spectra of mainshocks and aftershocks

3 有限元模型的建立

3.1 模型的建立

本文的結構分析模型采用OHTORI 等［20］提供的9 層benchmark 模型，如圖2 所示，結構設計滿足1994 年的美國統一建筑規范的設計要求。雖然結構沒有被真實建造，但是作為SAC的benchmark模型，能夠提供大量的對比研究。結構的外圍被設計為抗側力框架，內部為抗剪連接的承重框架，選取N-S方向的一榀水平抗力框架進行分析。

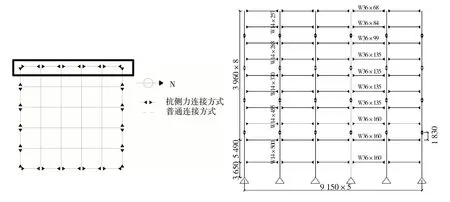
圖2 9層benchmark模型Fig.2 9-story Benchmark model

鋼框架使用SAP2000有限元軟件進行建模和非線性分析，梁柱構件為彈性單元，節點采用FEMA-365推薦的集中塑性鉸進行連接，塑性鉸位與距離節點0.1倍的桿件長度，柱底與基礎采用剛性連接。

3.2 模型驗證

彈性階段：結構的前三階周期分別為2.26 s、0.85 s和0.49 s，相對誤差分別為0.4%、0.35%和1.02%。

非線性階段：選取El Centro和Northridge兩條地震波進行結構分析，并與文獻［19］結果進行對比來驗證模型的準確性，結果見表2，最大誤差為9.21%，本文模型計算的結果總體上與文獻［19］相吻合，保證了模型的準確性。

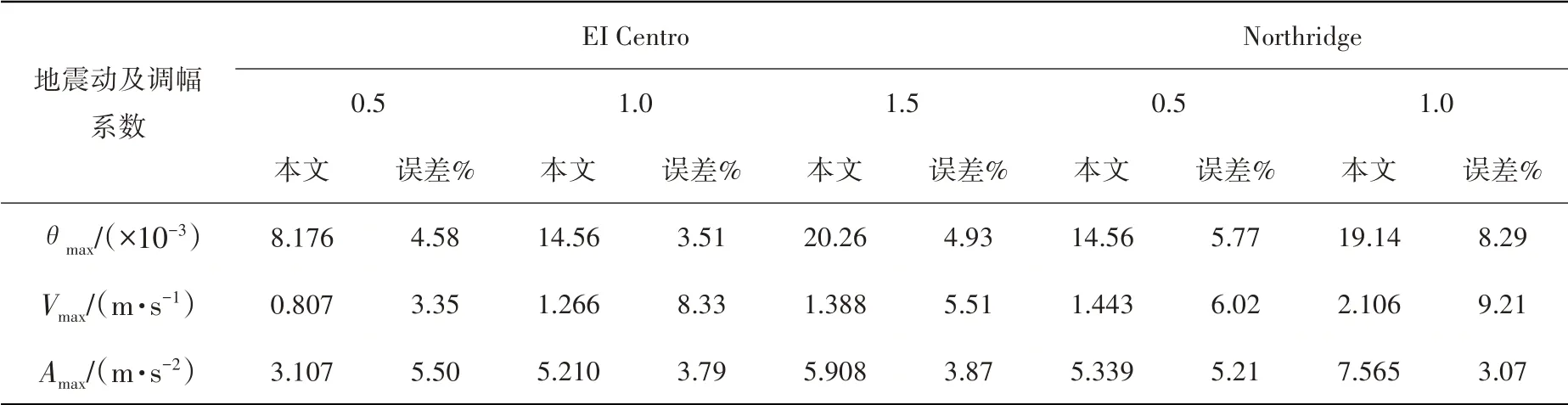
表2 地震作用計算結果的對比Table 2 Comparison of calculation results of seismic records

4 余震IDA曲線

4.1 結構損傷指標的確定

主震對結構損傷的準確量化，在余震易損性分析中至關重要，最大層間位移角是最為廣泛使用的結構損傷指標，能夠體現結構層間和整體位移延性的性能。最大殘余層間位移角在結構抗震性能評估中扮演著越來越重要的角色，結構震后殘余位移直接影響到震后是否需要加固以及加固成本［21］。哪一指標對主震損傷結構的判定更加準確，需要進一步討論。表3 分別為FEMA-273［22］以最大層間位移θmax和FEMA-P58［23］以最大殘余層間位移角θres作為結構損傷定義限值。

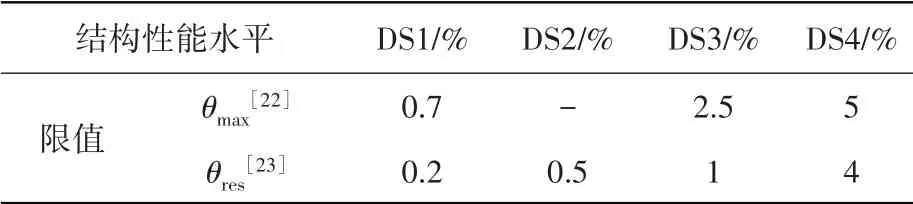
表3 結構需求指標的性能水平限值Table 3 Performance level limit of structural demand index

圖3（a）給出了主震分別以θmax和θres作為結構需求指標的IDA 簇。以θres為結構需求指標的IDA 簇與θmax相比，明顯更小，結構在達到最大位移之后，會有一定的位移恢復，隨著地震強度的增大，越接近倒塌，殘余位移和最大位移的IDA 曲線重合。單獨取一條IDA 曲線為例，分別標出各性能水平的限值，見圖3（b），DS1狀態下，Sa-res為0.25 g，Sa-max為0.09 g；DS3 狀態下，Sa-res為0.37 g，Sa-max為0.31 g；DS4 狀態下，Sa-res為0.92 g，Sa-max為0.66 g。θmax為結構需求的限值比θres保守，結構未發生殘余位移，說明結構還沒有屈服，未進入彈塑性階段，θres比θmax作為結構的DS1 狀態的限值更為準確，及沒有明顯的結構損傷；DS4 狀態定義為結構接近倒塌，以θmax限值作為界定，遠未達到結構接近倒塌的狀態及IDA 曲線接近水平段，θres更能夠反應結構的真實的DS4狀態。所以本文選擇最大殘余層間位移角θres作為主震對結構造成損傷量化的結構需求指標，余震的結構需求指標依舊采用最大層間位移角θmax。

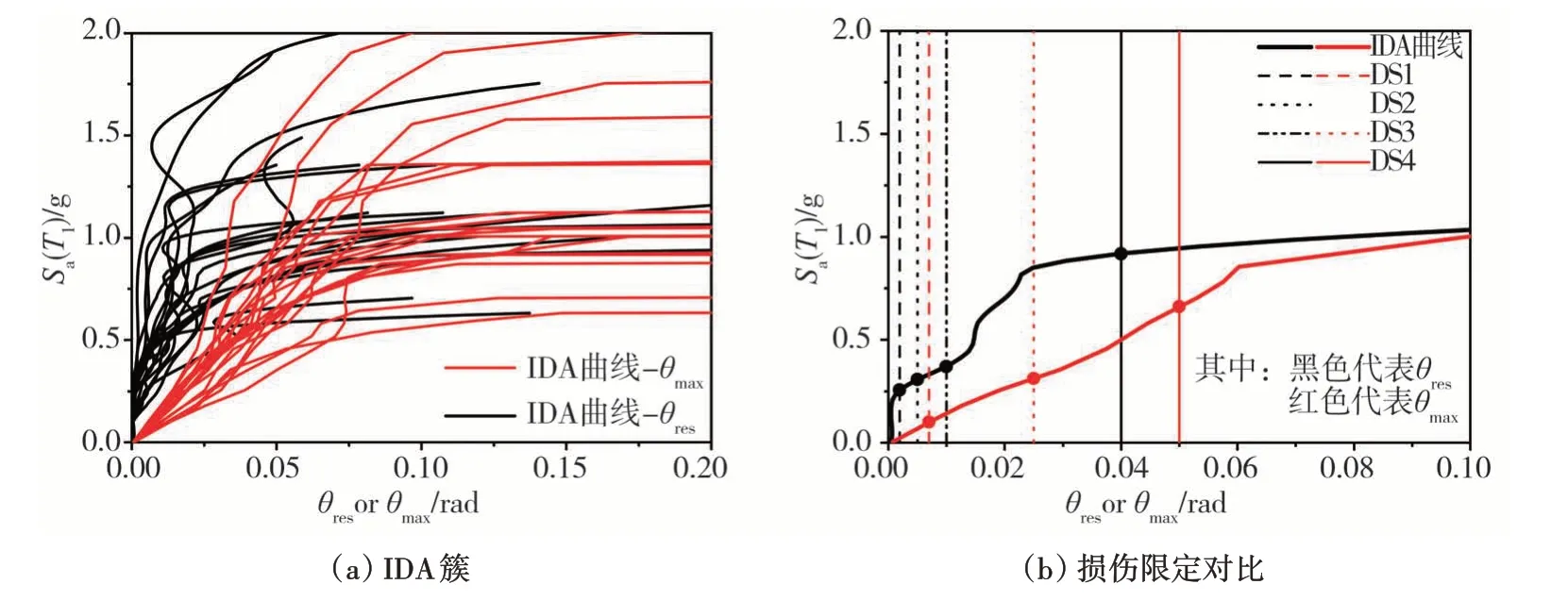
圖3 θmax 和θres作為損傷指標對比圖Fig.3 Comparison of θmax and θres as damage indexs

4.2 各性能水平下的余震IDA曲線簇

結構的余震分析前，首先需要將主震作用到結構上，使其分別達到完好無損和DS1～DS4 5 種結構初始性能水平狀態。主震和余震之間具有不同的極性［24］，當方向相同時，余震加劇結損傷，相反，會提高結構的抗倒塌能力，本文采用最不利狀態及正極主余震進行結構在余震作用下的IDA 分析。圖4 給出了5 種不同初始性能水平狀態下的余震IDA簇。余震IDA曲線的起點為主震造成的最終殘余位移。

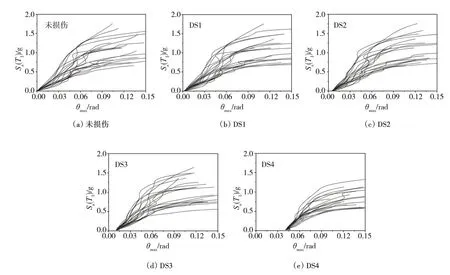
圖4 各初始性能狀態下IDA曲線簇Fig.4 IDA curves in different damage states

5 各地震動強度指標的對比

5.1 有效性評價指標

本文分別從離散性和相關性兩個方面評價地震動強度指標的有效性：離散性越小，使結構達到相同損傷時，各地震動之間的變異性越小；相關性越高，給定一組地震動之后，可以更加準確地預測結構的需求。

因為各IM 值之間的量綱和尺度不同，直接使用標準差來評價并不合理，本文采用變異系數指標Cv作為評價指標，消除了尺度和量綱的影響，更具有客觀性。在多條地震動下的IDA 簇中，特定結構需求下各條地震動的強度符合對數正態分布，其概率密度函數為：

式中：x為多條地震動使結構達到同一損傷狀態的IM 值；σ 為取對數之后的標準差；μ為取對數之后的平均值。

其變異系數Cv（X）的公式為：

相關性采用Pearson系數的r值來評價指標，其公式為：

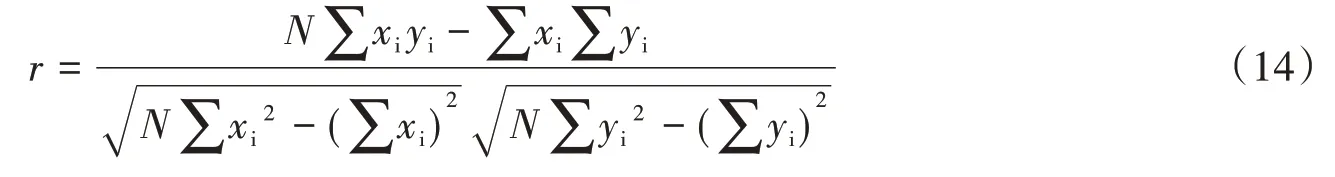
式中：xi為地震動強度指標的對數值；yi為結構需求指標的值。

5.2 離散性對比

結構確定的前提下，每條地震動都有唯一固定的地震動強度值，不隨其他因素變化而改變，所以只需計算一種地震動強度下的IDA 曲線，本文以譜加速度Sa（T1）作為IDA 計算時的地震強度指標，其余地震動強度下的IDA 曲線通過IM/Sa（T1）進行換算求的。再通過式（13）計算得到變異系數Cv，進行離散性的評價，圖5給出了不同性能水平下，各地震動強度指標的變異系數。可以看出譜加速度Sa（T1）對應平均變異系數為0.35左右，各個初始性能狀態下差距不大；基于一段周期內譜加速度幾何平均數的IMBoj&Lev結果最優，對各個初始性能狀態都能夠顯著減小IDA 曲線的離散性，對應的變異系數為0.25 左右，相對于譜加速度Sa（T1），離散性顯著降低了30%左右。其次是IMNav&Hall，在未損傷、DS1 和DS2 狀態下，θmax小于5%時，變異系數與IMBoj&Lev接近；θmax大于5%時，離散性增加，與Sa（T1）接近，在DS3 和DS4 狀態變異系數分別為0.25 和0.26 左右。離散性其余的IM指標與譜加速度Sa（T1）相比，對離散性減少程度有限，有些甚至會加大離散性。

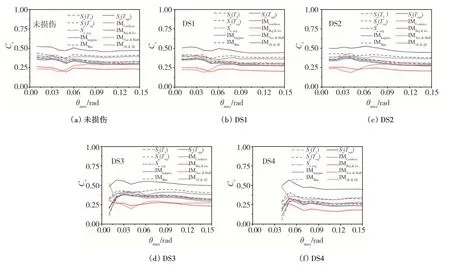
圖5 各初始性能狀態下IM指標的變異系數CvFig.5 Coefficient of variation Cv for IM in different damage states

5.3 相關性對比

根據IDA曲線，采用公式（14）分別計算10個地震強度指標在不同初始性能水平下的相關系數r，見圖6。當結構未損傷時，譜加速度Sa（T1）比其他地震動強度指標具有更強的相關性，其相關系數r=0.89，其他地震動強度指標的相關系數r在0.82～0.89；當主震對結構造成初始損傷，IMBoj&Lev和IMNav&Hall兩個地震動強度指標的優越性顯現，相比較與其他地震動參數，相關性更強，IMBoj&Lev和IMNav&Hall在DS1和DS2狀態下的相關系數r=0.93，DS3和DS4狀態下相關系數分別為0.90、0.84，譜加速度Sa（T1）在DS1和DS2狀態下的相關系數r=0.88，DS3狀態下r=0.84，DS4狀態下r=0.80，IMBoj&Lev和IMNav&Hall相對于譜加速度Sa（T1），相關性平均提高了6%左右。

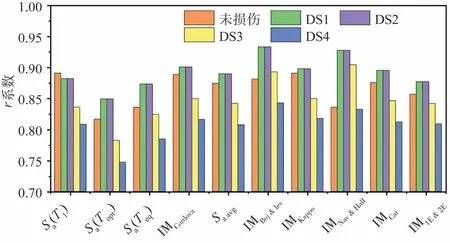
圖6 各IM指標的在不同性能水平的相關系數Fig.6 Pearson coefficients of IM in different damage states

隨著損傷程度的增加，同一地震動強度指標下，與結構需求指標的相關性下降，以譜加速度Sa（T1）為例，相關系數由r=0.88（DS1 狀態和DS2 狀態）分別下降到r=0.84（DS3 狀態）和r=0.80（DS4 狀態），最大下降了9%。圖7 給出了DS3 和DS4 狀態下以譜加速度Sa（T1）為例的地震動強度和結構需求指標的關系，從圖中可知隨著結構初始損傷的加劇，圖中的散點彎曲程度增加，地震強度指標和結構需求指標的對數線性相關性減弱，解釋了圖6中結構相關系數從DS1到DS4逐漸減小和IMBoj&Lev指標對相關性指標提高不顯著。

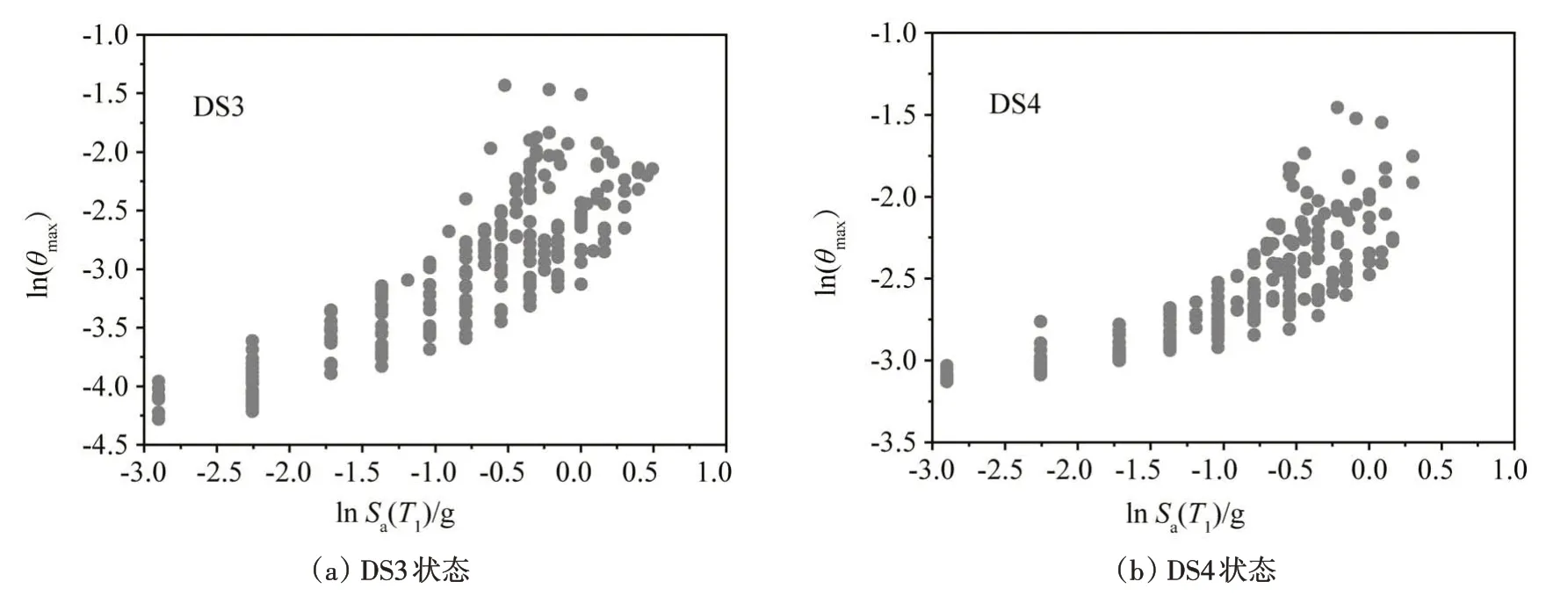
圖7 Sa（T1）和θmax的對數關系Fig.7 Logarithmic relationship of Sa（T1）and θmax

6 結論

本文通過選取20條集集地震的真實主余震序列，以9層benchmark鋼結構框架作為研究對象，探討了10種地震動強度值指標在主震損傷結構的余震IDA 分析中的優劣性，同時討論了最大層間位移角θmax和最大殘余層間位移角θres這兩種結構需求指標在主震對結構造成的損傷量化的選取。得出以下結論：

（1）最大殘余層間位移角θres更能夠準確地量化表示主震對結構造成的損傷，在余震分析中建議采用。

（2）IMBoj&Lev指標在各個初始性能水平狀態下，余震IDA 曲線簇的離散性最小。相對于Sa（T1），離散性降低了30%左右；其次是IMNav&Hall指標，但對應各個性能水平狀態下的離散性提高不太穩定。

（3）IMBoj&Lev和IMNav&Hall指標相對于其他地震強度指標，能更好地預測主震損傷結構余震地震動強度指標和結構需求指標的關系，比譜加速度Sa（T1）的相關性提高了6%左右；譜加速度Sa（T1）對未損傷結構具有更好的相關性預測。

（4）隨著主震對結構初始損傷的加劇，地震動強度指標和結構需求指標之間的對數線性相關性減弱。