嫦娥五號探測器多圈調相地月轉移應急軌道設計與分析

曹鵬飛，劉 勇，馬傳令，陳 明

(1. 北京航天飛行控制中心，北京 100094；2. 航天飛行動力學技術重點實驗室,北京 100094)

0 引 言

2020年12月17日，嫦娥五號返回器準確著陸于內蒙古四子王旗預定著陸區，至此，中國探月工程三期“繞”、“落”、“回”圓滿收官。此次嫦娥五號任務采用CZ-5運載火箭，于海南發射場發射，歷經發射段、地月轉移段、近月制動段、環月飛行段、著陸下降段、月面工作段、月面上升段、交會對接段、環月等待段、月地轉移段、再入回收段等11個階段，標稱軌跡控制為29次。

在任務準備時期，針對關鍵控制過程的應急軌道設計與標稱軌道設計同等重要。尤其是探測器入軌、近月制動、動力下降、月面起飛等決定任務成敗的關鍵弧段，必須給予充分的故障預案。嫦娥五號發射段，也稱上升段，指從運載火箭點火起飛開始至探測器與運載火箭分離為止，將探測器射入近地點高度約200 km，遠地點高度約38萬km的地月轉移軌道。在上升段末期，火箭二級發動機二次開機，軌道半長軸迅速增大，若期間火箭發動機發生提前關機故障，將直接導致探測器入軌(能量)半長軸不足。倘若半長軸偏差比較小，通過中途修正控制即可對軌道進行矯正；但當半長軸偏差比較大時，中途修正所需推進劑可能超出探測器余量，影響后續任務正常執行。針對該問題，文中提出多圈調相地月轉移軌道應急策略。

多圈調相地月轉移軌道的應用早期可追溯至中國嫦娥一號任務，其于2007年10月24日由長征三號甲(CZ-3A)運載火箭發射升空，之后進入繞地飛行的調相軌道。在經歷遠地點周期調整和近地點兩次較大機動后，分別進入周期為16 h、24 h、48 h的調相軌道，于地月轉移窗口打開時再次回到近地點，施加較大機動進入地月轉移軌道，于11月5日進入月球捕獲軌道，成為中國首顆月球衛星。嫦娥一號衛星通過逐步增加繞地軌道周期實現地月轉移，三次比較大的機動均是在近地點執行，對半長軸的抬升效率近乎最高。此次嫦娥五號任務，采用入軌直接地月轉移策略，但在應對火箭發動機提前關機故障時，嫦娥一號任務的轉移策略仍很有借鑒意義。

目前，關于月球轉移軌道的研究多集中在地月轉移軌道和月地轉移軌道部分。隨著火箭運載技術的發展，現月球探測任務多為入軌后直接地月轉移，而多圈調相地月轉移軌道需要在調相軌道等待數圈，總時間較長，因此相關研究和應用較少。國內較早有楊維廉等在嫦娥一號任務中較為詳細地給出了整體飛行軌道設計思路和調相軌道設計方法。國外較早由Dunham等、Uesugi等、Carrington等將調相思想引入探月飛行中，發現可以降低地月轉移燃料消耗并能擴展發射窗口等。因此，多圈調相地月轉移軌道多應用于早期火箭運載能力有限的探月任務，但在中國即將執行的探月四期和已進入“關深”階段的載人登月任務中，仍具有重要的應用價值，其軌道設計方法與軌道特性仍需進一步研究。

針對嫦娥五號任務上升段火箭二級發動機可能出現的提前關機故障，或發生入軌大偏差導致中途修正速度增量超限等問題，提出了多圈調相地月轉移控制策略。首先分析了不同入軌半長軸偏差、不同中途修正時刻與中途修正速度增量消耗之間的關系；其次，基于月球公轉周期，設計了解析窗口搜索與多圈調相地月轉移軌道一體化求解算法，實現了調相圈數、調相周期的快速規劃與地月轉移軌道的聯合求解，有效降低了速度增量消耗。通過實例，驗證了策略的正確性與可行性，并通過大量仿真算例分析了軌道特性。研究結果可應用于后續中國月球探測任務入軌期間的故障預案設計。

1 動力學模型

月球采樣返回任務背景復雜且工程要求苛刻，軌道求解精度要求更為嚴格。傳統的二體模型、雙二體模型和限制性三體模型等難以滿足軌道設計精度要求，必須考慮引入各種攝動加速度的高精度模型。

1.1 高精度動力學模型

在地心J2000坐標系中，考慮地球中心引力、日月引力攝動、地月非球形引力攝動和大氣阻力攝動等，探測器軌道動力學方程如式(1)所示：

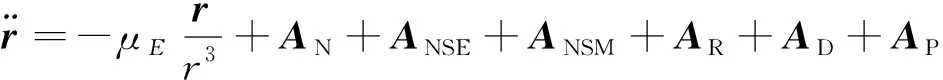
(1)

式中：為地心位置矢量；為地球引力常數；為N體引力攝動加速度，星體間空間幾何關系通過DE421星歷求解；為地球非球形攝動，取WGS84引力場模型6×6階計算；為月球非球形攝動，取LP165P引力場模型6×6階計算；為太陽光壓攝動；為大氣阻力攝動加速度；為推進加速度。忽略地球潮汐和相對論效應等微小攝動量的影響。

1.2 微分修正算法

微分修正算法和B平面參數在深空軌道設計中被廣泛應用，也是本文的基礎算法。

假設地月轉移軌道的約束變量為維的向量，控制變量為維向量。前者可根據月球探測任務目標軌道的要求而定；后者取轉移軌道修正點的軌道參數，一般為速度增量。二者之前存在函數關系，如下

=()

(2)

若控制變量初值為，對應的約束變量值為，將式(2)在處進行泰勒展開并取一階項，得：

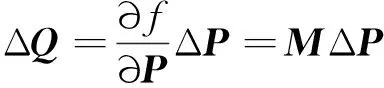
(3)

式中:為雅克比矩陣，反映了約束變量相對控制變量微小改變的敏感性，工程任務中可采用差分法進行數值求解。

已知與目標約束存在一定偏差-，則利用式(3)，可迭代計算出修正-所需的Δ，如下式

Δ=Δ

(4)

若≠，則可利用最小范數廣義逆計算Δ，如下式

Δ=(·)Δ

(5)

關于B平面參數的內容可參考文獻[8,19]，限于篇幅，這里不再進一步展開介紹。

1.3 火箭發動機提前關機故障對入軌影響分析

火箭發動機提前關機故障主要影響入軌軌道的半長軸和偏心率，對其它軌道參數影響不大。如圖1所示，給出了嫦娥五號任務上升段后期入軌半長軸隨時間變化趨勢圖。

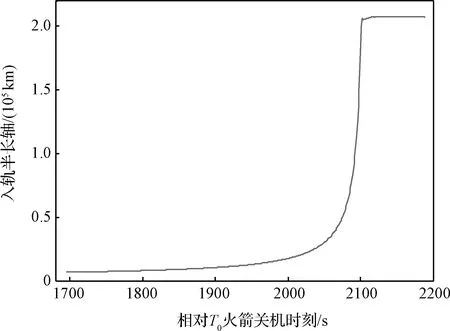
圖1 二級二次點火后半長軸變化趨勢圖Fig.1 The change trend of the semi-major axis after the secondary ignition of the secondary engine

由圖1可知，探測器正常入軌時刻為，在前約400 s內，軌道半長軸隨時間的推移近似指數增長，從約6×10km增加至約2×10km。若期間，火箭發動機發生提前關機故障，通常制定如下應急控制策略：1)在+17 h實施中途修正控制，繼續完成后續飛行任務；2)若半長軸偏差較大，提前實施中途修正控制，繼續完成后續飛行任務。如圖2所示，給出了不同提前關機時刻、不同中途修正時刻(相對)，中途修正消耗的速度增量變化情況。

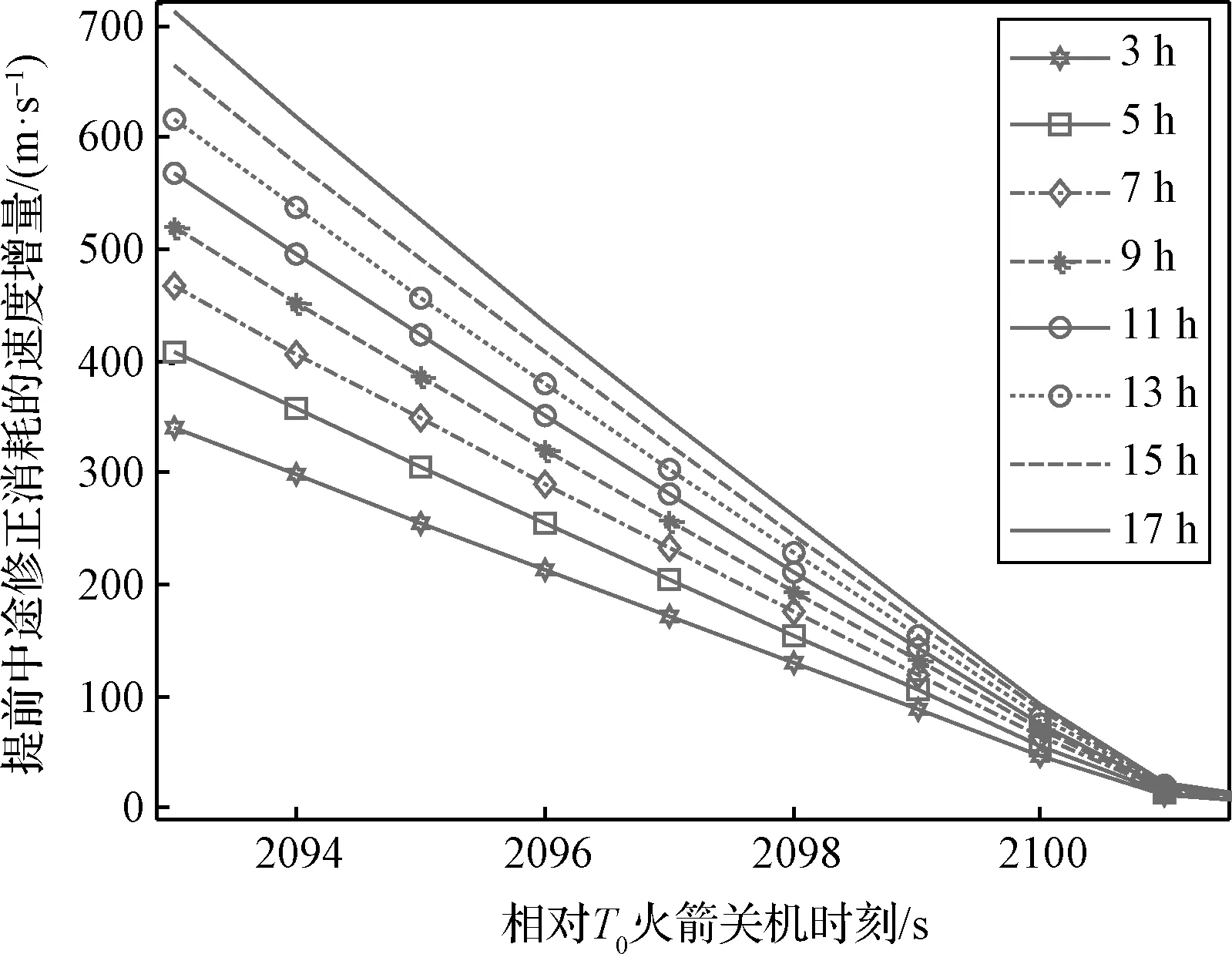
圖2 不同提前關機時刻、不同中途修正時刻對應速度增量消耗變化趨勢Fig.2 The change trend of incremental speed consumption corresponding to different early shutdown time and different midcourse correction time

由圖2可知，火箭發動機提前關機故障發生時機越靠前、中途修正時刻越靠后，中途修正消耗速度增量越多。嫦娥五號探測器標稱入軌半長軸為206817.8 km，若發生火箭發動機提前關機故障，在保證完成后續采樣返回任務的前提下，地月轉移段最大可用速度增量約為173 m/s。以此為上限，對比圖2和圖1可計算出不同中途修正時刻，對應的最小半長軸和最大入軌半長軸偏差Δ，結果見表1。

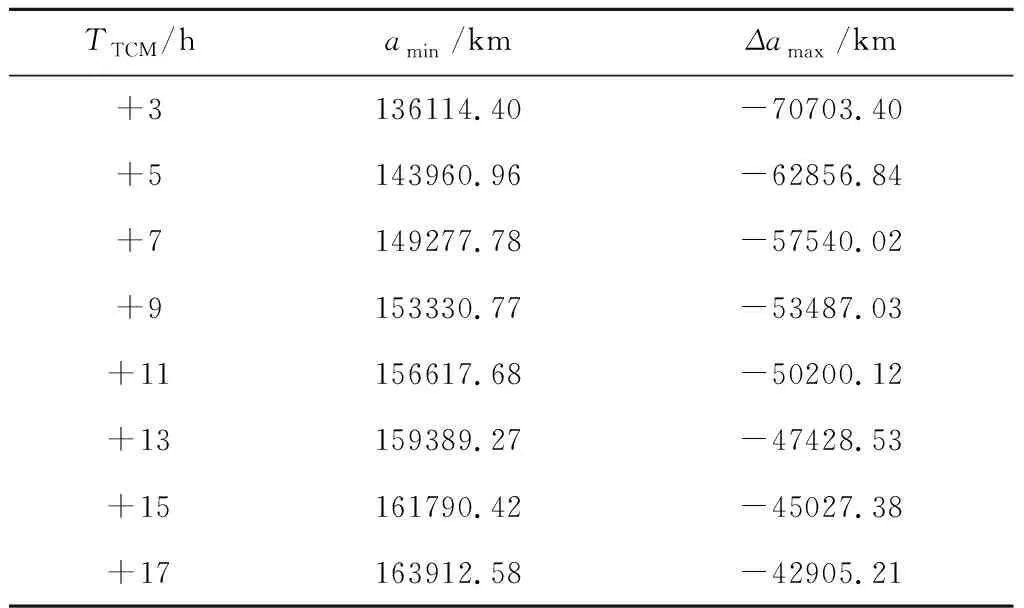
表1 不同修正時刻對應的最大半長軸偏差Table 1 The maximum semi-major axis deviation corresponding to the different midcourse correction time

由表1可知，中途修正時刻越靠后，所能修正的半長軸偏差越小。+3 h中途修正控制對應的最大半長軸偏差約為7.070×10km，若半長軸偏差進一步增大，中途修正消耗的速度增量將超限。

2 多圈調相地月轉移軌道設計

針對月球探測器入軌半長軸偏差超出中途修正能力問題，本節給出多圈調相地月轉移軌道方案，并制定高精度模型下的求解策略。

2.1 多圈調相地月轉移軌道方案

在進行月球探測任務發射窗口規劃時，為應對可能出現的火箭推遲發射等情況，通常要求至少連續兩個月存在發射窗口。

若當月窗口的上升段出現火箭發動機提前關機故障導致半長軸偏差過大超出中途修正能力，或入軌后出現短期內無法排除的故障等，均可采用多圈調相地月轉移軌道方案。如圖3所示，給出一個典型的多圈調相地月轉移軌道示意圖。由于火箭發動機提前關機，探測器入軌后進入半長軸偏差較大的繞地橢圓軌道，運行一圈再次到達近地點時施加調相機動進入調相軌道，在調相軌道上運行數圈于最后一次到達近地點時施加地月轉移機動進入地月轉移軌道，之后擇機實施中途修正控制以修正定軌和控制偏差，到達近月點時實施近月制動被月球捕獲。

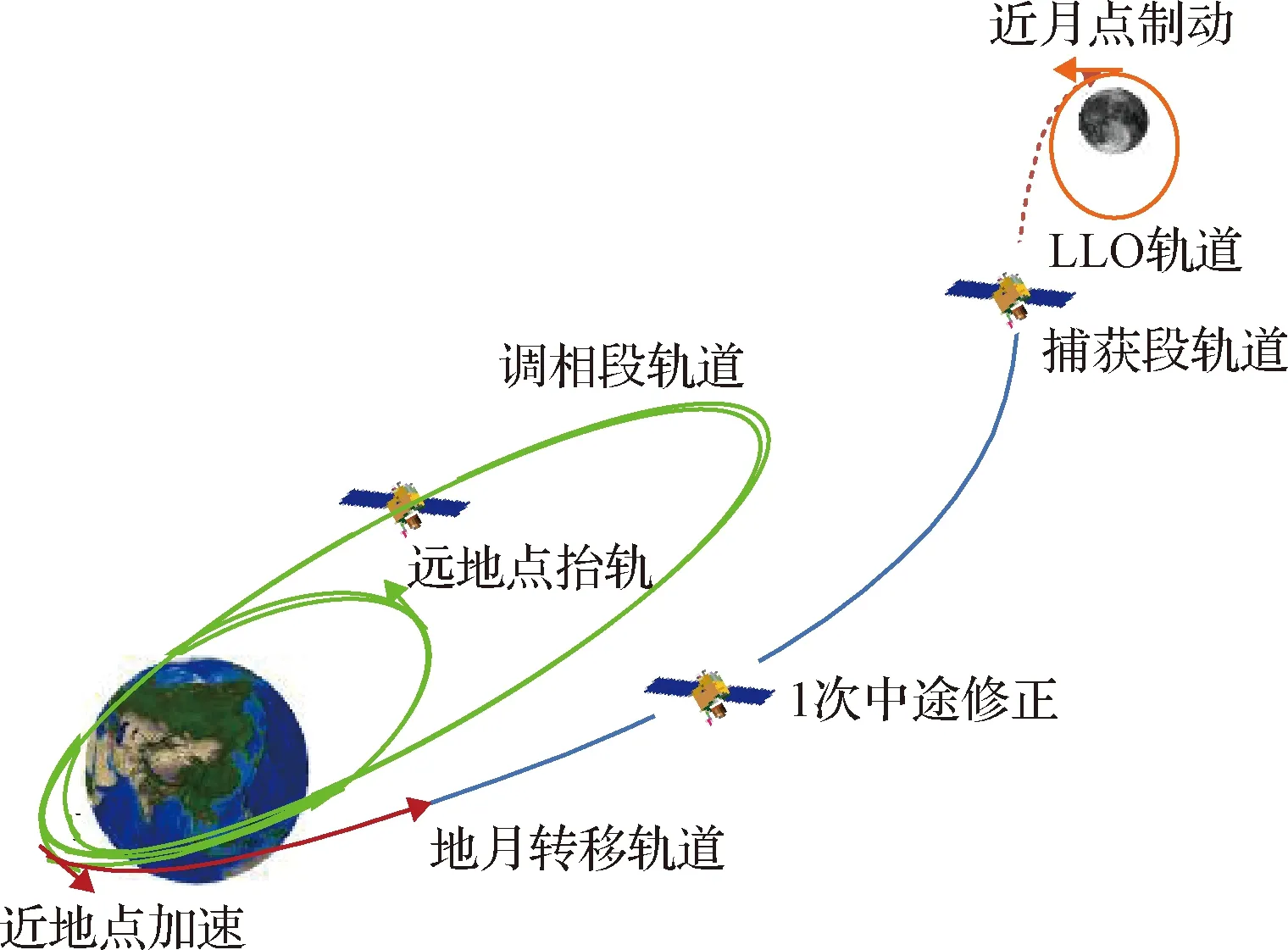
圖3 多圈調相地月轉移軌道示意圖Fig.3 Diagram of the multi-cycle phase modulated Earth-Moon transfer trajectory

2.2 多圈調相轉移軌道優化模型

下文從設計變量、約束條件和目標函數三方面給出多圈調相地月轉移軌道優化模型。

由圖1可知，火箭發動機提前關機故障發生時機不同時，入軌對應的半長軸偏差也不同。本節給出適用于不同半長軸偏差的多圈調相地月轉移軌道規劃模型。設計變量為：近地點高度、遠地點抬升機動脈沖Δ、總轉移時間Δ(包含調相段時間與地月轉移時間)、調相軌道圈數、調相機動時刻、調相軌道周期Δ、調相機動脈沖Δ，以及地月轉移時刻、地月轉移時間Δ、地月轉移機動脈沖Δ。上述設計變量均已知時，在高精度模型下可確定一條多圈調相地月轉移軌道。

下文給出各設計變量確定方法，一般由任務給定，參考嫦娥一號任務取600 km；選在探測器入軌后首次回到近地點的時刻；選在探測器最后一次過近地點的時刻；Δ與可由式(6)確定，如下

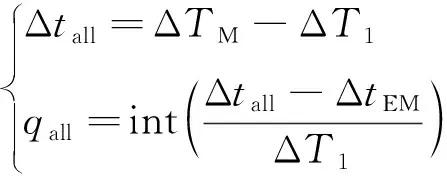
(6)

式中：Δ為月球公轉軌道周期，取27.32 d；Δ為入軌偏差軌道周期，根據定軌結果確定；int為向下取整符號。由與Δ，進一步可由式(7)確定Δ，如下

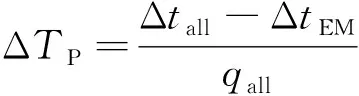
(7)

因此，一條多圈調相地月轉移軌道可由式(8)所示的四個元素確定，即

=[Δ,Δ,Δ,Δ]

(8)

由于多圈調相地月轉移軌道瞄準下個月奔月，總的轉移時間相對固定，這里以總速度增量消耗為優化目標，即目標函數為

min=Δ=Δ+Δ+Δ

(9)

2.3 多圈調相轉移軌道求解策略

針對上述優化模型求解問題，提出如下控制策略，具體流程如圖4所示。

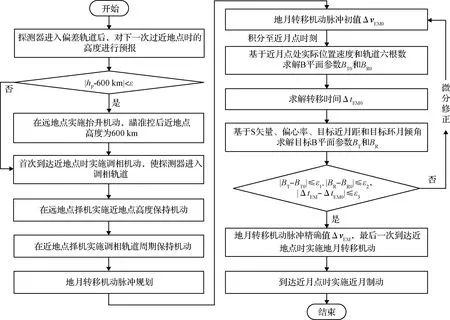
圖4 多圈調相地月轉移軌道求解流程圖Fig.4 Solution flow chart of the multi-cycle phase modulated Earth-Moon transfer trajectory

(1)遠地點機動抬高近地點。受大氣阻力、月球引力等攝動影響，探測器在偏差軌道上運行一圈后可能存在撞地風險。因此，入軌后應首先對下一次過近地點時的高度進行預報。若高度低于600 km，則在遠地點施加機動脈沖Δ，將近地點抬高至600 km；反之，則取消機動脈沖Δ。

(2)近地點機動進入調相軌道。根據式(6)和式(7)規劃與Δ，期間為避免推進劑額外消耗，應以升軌調相為主，即調相軌道半長軸大于入軌偏差軌道半長軸。若調相軌道的遠心距大于地月距離，可以考慮降軌調相。

(3)遠地點高度保持。探測器在調相軌道運行期間，每一圈均需進行近地點高度預報，若高度低于600 km，則需在遠地點實施抬升機動，脈沖記為Δ，將近地點抬高至600 km，否則進入(4)。

(4)近地點周期保持。預報圈后探測器最后一次到達近地點的時刻，若與偏差較大，則需在近地點實施周期保持機動，脈沖記為Δ，否則進入(5)。

(5)近地點地月轉移機動。在探測器到達地月轉移入口時，施加Δ進入地月轉移軌道，瞄準地月轉移時長、到達近月點時的高度和月固系軌道傾角為標稱值。在求解Δ時，可采用二體活力公式解析求出初值Δ，然后在高精度模型下將近月點高度約束與傾角約束轉化為B平面參數，采用微分修正策略迭代求解。

(6)中途修正。根據近月點參數偏差情況擇機安排中途修正控制，控制目標與地月轉移機動相同。

(7)近月制動。探測器到達近月點時，實施近月制動控制，以實現月球捕獲，控制目標是目標半長軸。

3 實例驗證與軌道特性分析

3.1 多圈調相地月轉移求解策略校正

以嫦娥五號任務2019年窗口上升段末期彈道為例給出設計實例，參數配置如下：探測器標稱入軌時刻為9 Nov 2019 07∶26∶24.061 LCLG，由于發射火箭提前關機故障造成入軌時刻為9 Nov 2019 07∶24∶50.105 LCLG，軌道六根數見表2。其中，為半長軸，為偏心率，為軌道傾角，為升交點赤經，為近地點幅角，為真近點角。半長軸偏差約9.88×10km，由表1可知，該半長軸偏差已超出+3 h中途修正能力。

表2 地心J2000坐標系下軌道根數Table 2 The orbit elements under the J2000 coordinate system

以上述偏差軌道為輸入，地月轉移時間設為112 h，采用2.3節的求解策略，計算多圈調相地月轉移軌道，得到的軌道飛行軌跡如圖5所示，相應的軌道參數及各次機動消耗的速度增量見表3。其中，Δ為近月制動速度增量；為到達近月點時刻，日期為11 Dec 2019 00∶00∶00.000 LCLG。

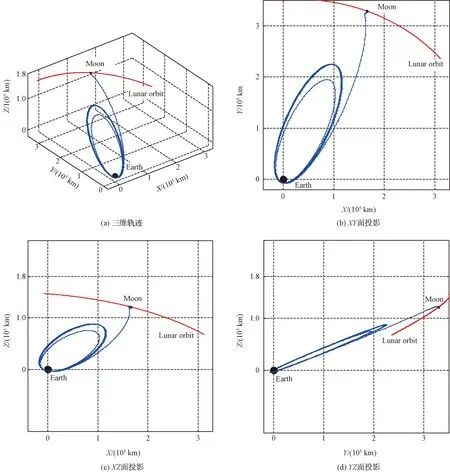
圖5 J2000坐標系下不同視角的多圈調相地月轉移軌道飛行軌跡Fig.5 Multi-cycle phase modulated Earth-Moon transfer trajectory with different perspectives under the J2000 coordinate system

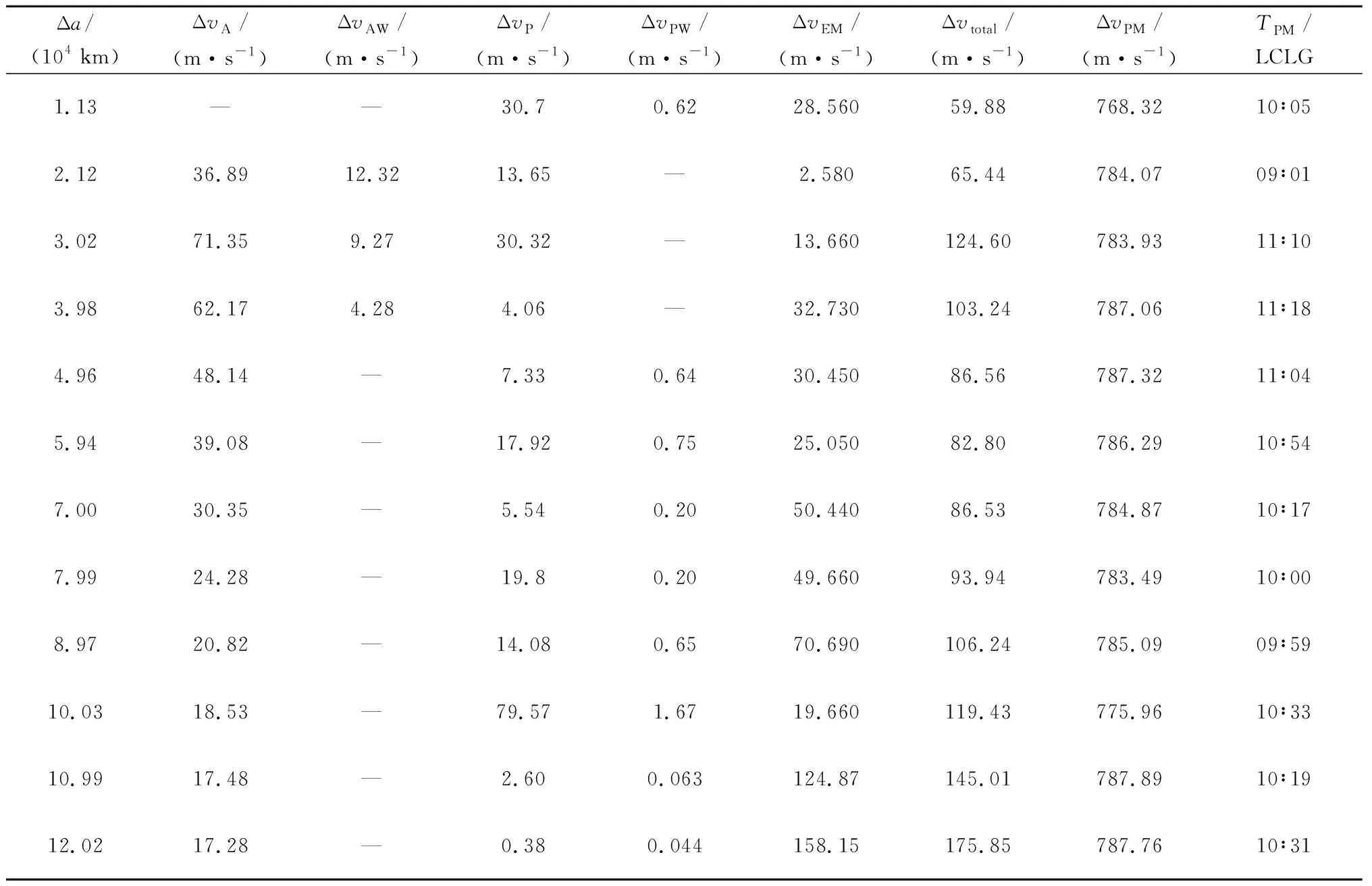
表3 多圈調相地月轉移軌道參數Table 3 The orbit parameters of multi-cycle phase modulated Earth-Moon transfer trajectory

此計算過程在計算機CPU為2.67 GHz的Matlab環境下進行，單條軌道的計算時長不超過30 s。因此，利用該方法進行多圈調相地月轉移軌道設計時，收斂速度很快，適合用于大規模的軌道特性分析。

3.2 多圈調相地月轉移軌道特性分析

在任務設計階段，工程人員往往對單條軌道參數并不關心，而是更加注重這一類軌道的一般規律和特性。本節在3.1節算例的基礎上，取不同的火箭提前關機時刻，模擬不同的入軌半長軸偏差，范圍設置為1×10～1.2×10km，約以1×10km為步長，以此為輸入分析多圈調相地月轉移軌道特性。

首先，分析半長軸偏差和地月轉移速度增量消耗之間的關系。在二體模型下利用活力公式，解析計算入軌偏差軌道與遠地點在月球的轉移軌道在近地點處的速度差，從而得到地月轉移機動速度增量。

如圖6所示，給出了不同半長軸偏差對應的地月轉移機動速度增量變化趨勢圖。二體模型下，隨著半長軸偏差從1×10km增至1.2×10km，地月轉移機動所需的速度增量從0附近單調遞增至150 m/s，符合所需軌道能量隨半長軸偏差增大而增大的特性。

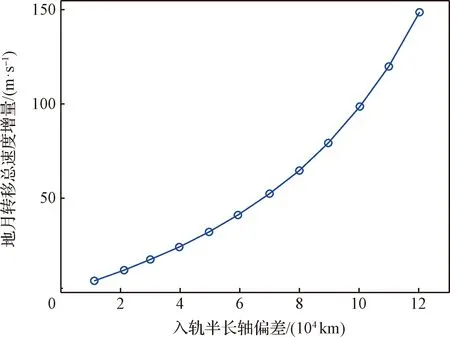
圖6 二體模型下半長軸偏差與地月轉移速度增量之間的關系Fig.6 The relationship between the semi-major axis deviation and the speed increment of the Earth-Moon transfer maneuver under the two body model

采用2.3節求解策略，逐條計算出由不同半長軸的偏差軌道出發，經多圈調相、地月轉移后，達到近月點的轉移軌道，各次機動消耗的速度增量、到達近月點的時刻信息見表3。對應的半長軸偏差與地月轉移段總速度增量之間的關系如圖7所示。

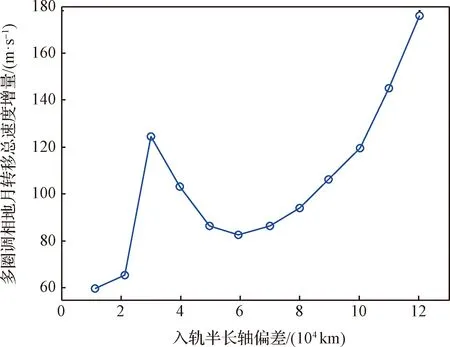
圖7 高精度模型下半長軸偏差與地月轉移段速度增量之間的關系Fig.7 The relationship between the semi-major axis deviation and the speed increment of the Earth-Moon transfer segment under the high precision model

由圖7可知：(1)與二體模型不同，高精度模型下多圈調相地月轉移段所需的速度增量隨著半長軸偏差的增大，并非單調遞增，而是呈先增大后減小再增大的變化趨勢；(2)當半長軸偏差約為3×10km，速度增量消耗達到極大值，當半長軸偏差約為6×10km，速度增量達到極小值；(3)半長軸偏差大于6×10km時，隨著半長軸偏差的增大，速度增量消耗也增大，這明顯是因為所需增大軌道能量隨半長軸偏差增大而增大的緣故。

3.3 月球引力攝動影響分析

仿真中發現，探測器在不同偏差軌道上運行，受地月關系影響，遠地點在月球影響球邊緣或進入月球影響球內時，易受月球引力影響被月球“加速”，或被月球“減速”，由此將導致探測器近地點高度抬升或降低。當軌道近地點高度低于一定程度時，需要進行近地點高度保持控制。為分析圖6與圖7所呈現特性差異的原因，分析半長軸偏差和近地點高度保持與抬升速度增量之間的關系，如圖8所示。

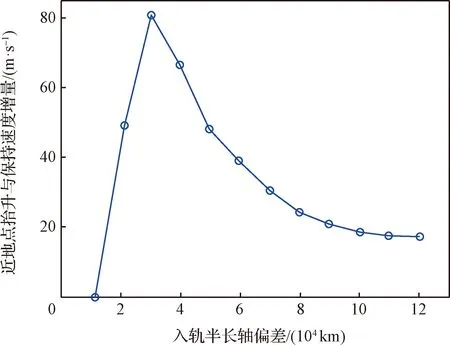
圖8 半長軸偏差與近地點高度抬升與保持的速度增量之間的關系Fig.8 The relationship between the semi-major axis deviation and the speed increment of perigee elevation and maintenance

由圖8可知：隨著半長軸偏差的增大，近地點高度抬升與保持的速度增量從0先急劇增大后緩慢減小，當半長軸偏差為3×10km，速度增量達到極大值。原因如下：當半長軸偏差為1×10km時，探測器在遠地點附近將被“加速”，近地點高度抬升無撞地風險，因此不需要進行高度保持控制；當半長軸偏差為3×10km，探測器在遠地點附近被“減速”最嚴重，由此導致近地點高度抬升與保持消耗的速度增量最多。

4 結 論

本文針對嫦娥五號任務上升段末期可能出現的火箭發動機提前關機故障，及半長軸偏差較大問題，提出了多圈調相地月轉移軌道應急控制策略。設計了解析窗口搜索與多圈調相地月轉移軌道一體化求解算法，有效降低了速度增量消耗，擴大了半長軸偏差適應范圍。并在仿真中發現，受月球引力攝動影響，多圈調相地月轉移段所需的速度增量隨著半長軸偏差的增大呈先增大后減小再增大的變化趨勢，在半長軸偏差約為3×10km時，地月轉移總速度增量消耗達到極大值。