環向肋增穩的薄壁圓筒結構定向拓撲優化方法

粟 華，陳偉俊，龔春林，李 鵬

(1. 西北工業大學航天學院,陜西省空天飛行器設計重點實驗室，西安 710072；2. 湖北航天技術研究院總體設計所，武漢 430000；3. 西安現代控制技術研究所，西安 710065)

0 引 言

飛行器結構總體設計通常在方案設計階段進行，該階段設計空間大、約束少，方案需要進行多輪迭代。因此，需要詳細結構模型求解緩慢的精確求解方法并不適合在該階段使用。廣泛應用于飛行器艙段的薄壁圓筒結構通常需要承受較大的軸向載荷，并且需減輕自重滿足質量約束，實際應用中常采用薄壁圓筒內加筋的結構形式，以較小的附加質量使結構滿足設計指標。這類結構的加筋形式將直接影響飛行器性能，因此發展一種高效快速適用于結構總體設計階段的，兼顧結構加工性與穩定性的薄壁圓筒內加筋結構形式優化設計方法具有重要意義。

傳統的薄壁圓筒加筋設計方法通常基于等效思想，通過經驗公式確定均布加筋的數目與形式。Phillips等、Wodesenbet等基于結構單胞的內力分析提出了改進的等效剛度模型。王博等基于單胞結構等效剛度使用漸進均勻化方法完成了薄壁圓筒結構的快速屈曲優化。基于等效思路的設計方法能夠實現結構的輕量化改進，但該類方法在設計伊始就確定了基本的加筋的布局形式，優化設計空間較小，優化能力有限。由于以最大剛度為目標的結構拓撲優化結果可以反映結構的傳力路徑，沿著此路徑布置材料可以獲得材料利用率高的輕質結構，基于拓撲優化的薄壁結構加筋形式設計方法表現出巨大的潛力。為了使拓撲優化結果具有適合薄壁結構加工的形式，Zhou等提出了一種考慮拔模約束的拓撲優化方法，可得到類拔模形式的薄壁加筋結構形式，但僅限于平面結構。張衛紅等提出了一種背景網格法,可以實現任意形狀的結構加筋方向拉伸約束的高質量加筋布局優化，但該方法需額外引入一套符合結構形貌的背景網格，造成前處理和求解困難。上述方法僅考慮了結構剛度最大化問題，并未考慮結構的穩定性。有研究者也在尋找兼顧薄壁結構穩定性的方法。郭中澤等、鐘煥杰均將結構的屈曲系數作為附加約束引入結構拓撲優化問題，減重的同時保證了結構穩定性要求。但是這些方法都會面臨較為復雜的特征值求解問題，計算耗時量較大導致其難以進行快速迭代，不適用于飛行器結構總體設計階段的研究工作。

為了解決上述不足，讓拓撲優化更加貼近工程實際，文中提出了一種高效快速且結果工藝性好，具有較好的工程應用價值的環向肋增穩的定向拓撲優化方法，如圖1所示。

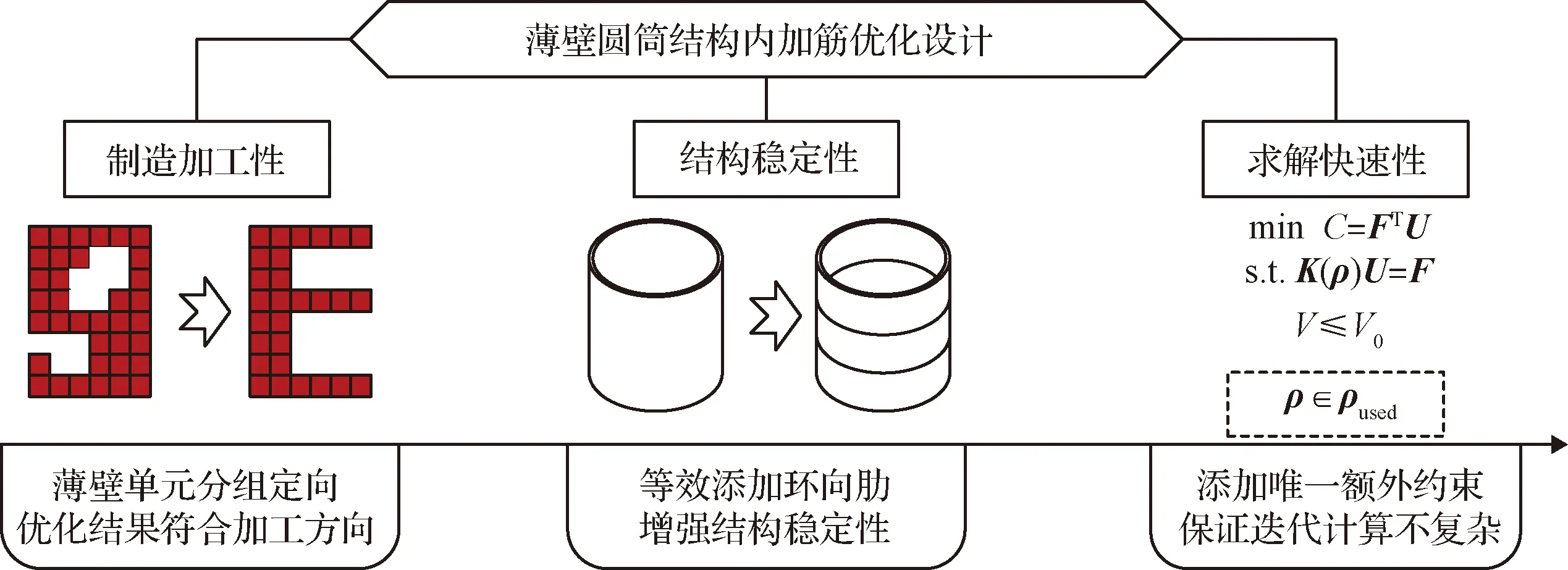
圖1 環向肋增穩的定向拓撲優化方法Fig.1 The characteristics and procedure of the oriented topology optimization of thin-walled structure with circumferential rib enhancement of stability

該方法通過對表面薄壁單元的定向分組，完成設計空間的重定義，保證優化過程中壁厚方向的一致性，使結果具有較好的加工性；通過添加環向肋結構進行穩定性增強；通過重定義撲優化設計空間，僅添加唯一的單元分組約束，避免了引入額外的復雜穩定性求解過程，保證求解快速性。

首先基于有限單元定向分組方法進行設計空間重定義，提出了確定環向肋和修正設計空間的方法；然后給出了該方法基于修正設計空間的剛度最大化拓撲優化模型；最后運用該方法對運載火箭級間段結構進行優化設計，得到了具有較好實用性的優化結果并與其他優化方法進行對比分析。

1 基于經典變密度法的結構拓撲優化問題定義

變密度法參數較少，迭代穩健，構造問題模型方便，是一種廣泛使用的通用拓撲優化方法，本文以該方法作為基礎展開研究。

變密度法使用相對密度量描述單元存在性與材料屬性之間的關系，使用相對密度概念將拓撲優化問題的設計變量從“0～1”離散型變量轉變為趨向兩端分布“0～1”連續變量，將不易求解的離散性問題轉化為容易求解的連續性問題。綜合考慮求解效率與結果準確性，選擇使用各項同性材料懲罰模型(SIMP)模型：

=

(1)

式中:為相對密度下的彈性模量;為材料真實彈性模量;為有限單元相對密度;為懲罰因子，綜合求解效率與結果的準確性;值取3。

對結構進行剛度最大化的拓撲優化設計，因結構的柔度與剛度為倒數關系，故該問題等效為結構柔度最小化設計問題。將柔度表示為單元密度的函數，構建體積約束下的最小柔順度問題模型：

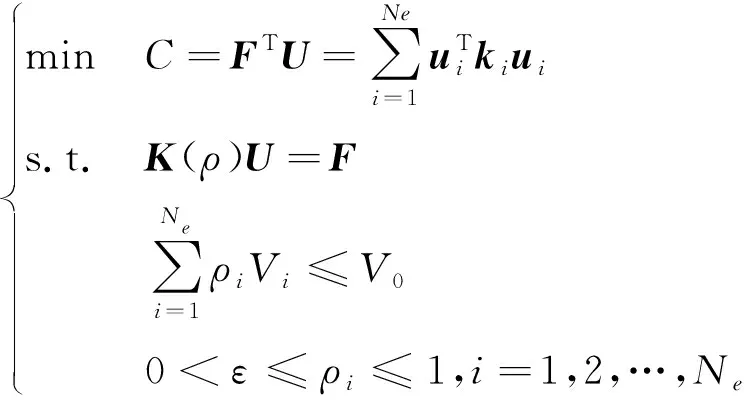
(2)

式中:為第號單元的相對密度;為避免相對密度為0造成求解困難的一小值;為設計域內單元總數;,和分別為總體剛度矩陣、位移向量和荷載向量;為第個單元的剛度矩陣，是相對密度的函數;是總體體積分數約束上限;是第個單元的體積。

目標函數對設計變量的敏感度為:

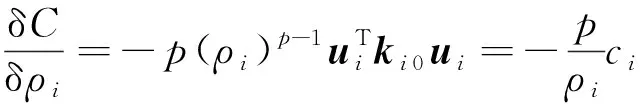
(3)

式中: 0為第個單元實際的剛度矩陣;為第個單元的應變能，負號表明向著柔度減小的方向進行。

2 依據表面單元的定向分組方法

變密度法將每個單元的相對密度作為設計變量，優化結果易存在內部空洞，所得結果雖然符合優化問題的約束，但不符合薄壁結構的實際加工特征。這里引入定向分組方法解決此問題。

飛行器艙段結構通常為薄壁蒙皮加筋形式，表面蒙皮厚度只有加筋高度的十分之一。因此常采用平面板單元模擬蒙皮區域，實體單元模擬加筋設計區域進行建模分析。由于結構的薄壁特性，實體單元可以依據外層平面單元的法向方向分成如圖2所示的若干單元組。

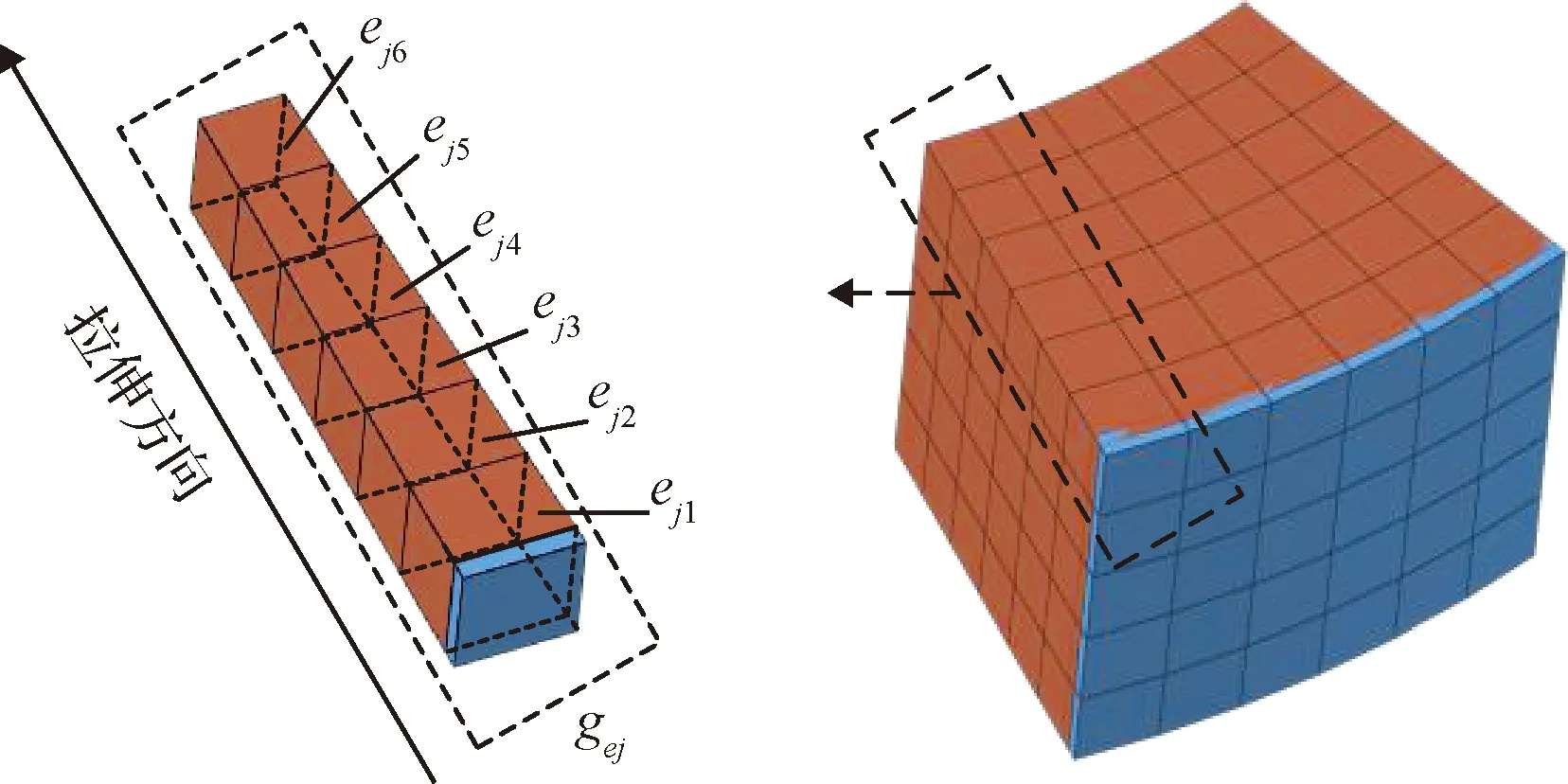
圖2 單元分組示意Fig.2 Illustration of elements group

圖中最外層平面單元組成的薄壁表面為非優化區域，內部的實體單元組成內壁優化設計空間。

基于這種分組方式進行的拓撲優化過程與使用機加或化銑手段的結構制造過程在空間形式上具有一致性，易于建立有限單元間的對應關系。并且該分組過程僅在模型前處理過程中只執行一次，迭代優化過程不會引入額外約束，工作量較小，計算速度較快。因此，以單元組作為設計空間基礎單位的拓撲優化方法可以在結構總體設計階段快速得到具有較好加工性的優化結果，下面給出分組的具體方法。

記圖2所示第組定向劃分的實體單元組為：

={1,2,…,}

(4)

式中:為單個有限單元信息;1至為同屬第分組的單元對應單元號。

記為第組單元的相對密度;為單元分組總數，同一組單元擁有相同的相對密度，即：

=1=2=…=，=1,2,…,

(5)

則有以“組密度”重定義的設計空間：

={1,2,…,}

(6)

至此，組成設計空間的基本單位從各有限單元的相對密度變為各單元組的相對密度，優化過程中將以單元組整體的有無進行迭代，保證了拓撲優化結果具有定向性。

3 引入穩定性增強的分組拓撲優化策略

由于薄壁結構容易發生屈曲失效，在考慮結構剛度的基礎上還應考慮薄壁結構的穩定性。本節將給出基于歐拉穩定理論的薄壁結構環向穩定性增強策略，并將其引入連續體拓撲優化中得到增強穩定性的定向分組拓撲優化方法。

3.1 穩定性增強策略

由于剛度最大化的拓撲優化結果將保留結構傳力路徑上的材料，在軸向載荷作用下總會存在部分縱向分布的材料以滿足結構剛度要求，而環向方向的材料是否保留沒有明確的規定，因此可以通過添加環向肋的方法進行穩定性增強。

在結構總體設計階段，通常基于無初始變形和缺陷的理想情況考慮薄壁圓筒類結構穩定性問題。大量試驗結果表明，對于這種情況，基于線性歐拉屈曲理論給出的薄壁結構整體屈曲臨界載荷與試驗結果符合較好。因此，可采用臨界應力公式快速計算薄壁結構的屈服載荷：

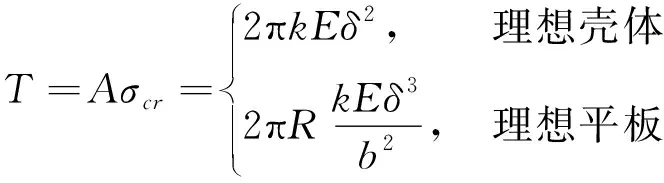
(7)

式中:為屈服載荷;為截面面積;為殼體半徑;為為臨界應力;為穩定系數(結構形式不同而不同);為材料彈性模量;為殼或板的厚度;為板發生屈曲方向的邊長。

確定環向肋的方法如下：

(1)環向肋位置確定

在初始設計階段首先應確保兩相鄰環向肋之間的壁板滿足局部穩定性，如圖3右上的單獨環狀壁板所示。圖中為薄壁圓筒結構總高度，其余符號同式(7)中含義。

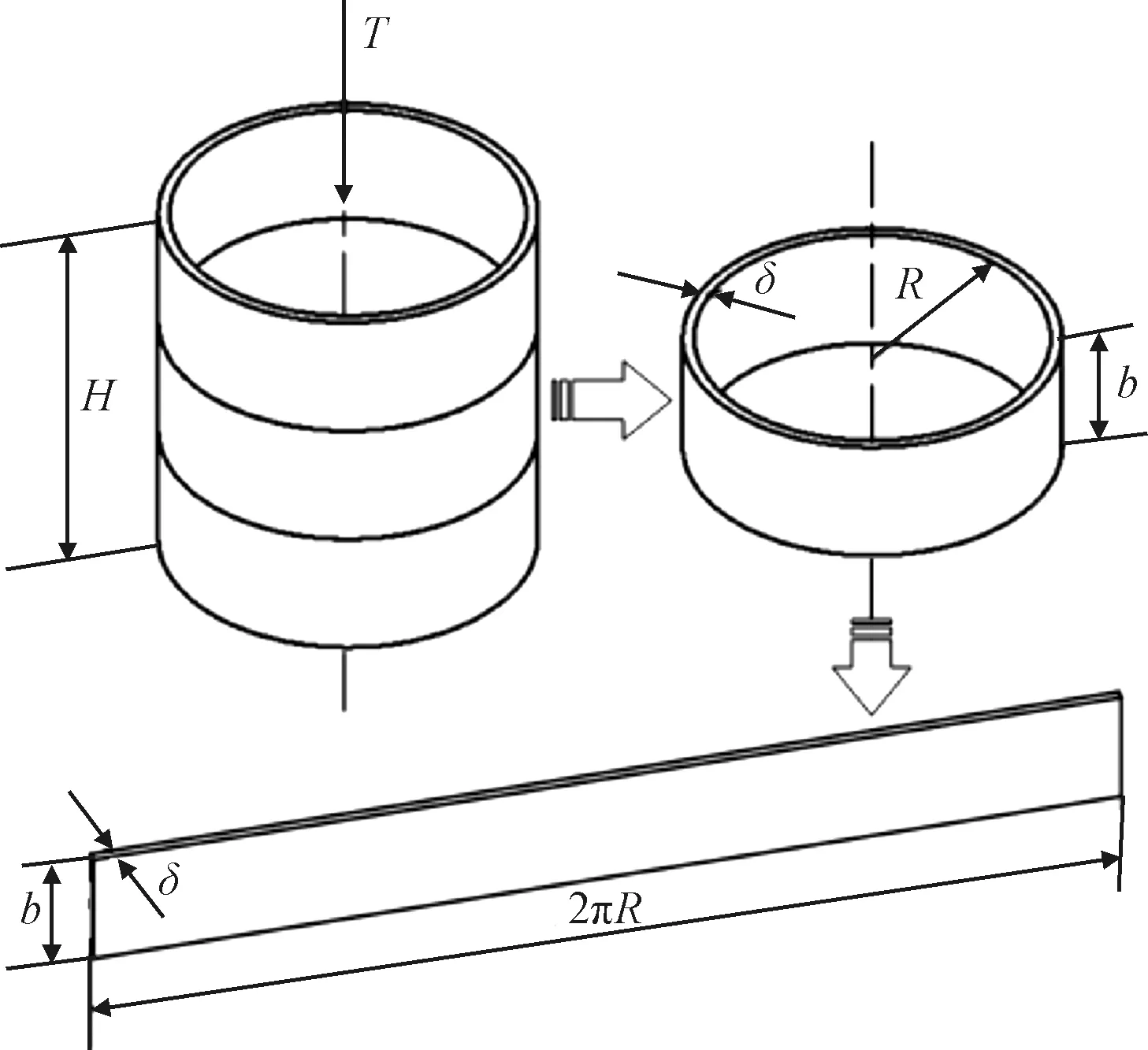
圖3 環向肋計算中相關參數示意Fig.3 Illustration of parameters used in calculating the number of circumferental ribs

由于薄壁結構壁厚和半徑相比很小，環向肋之間的局部穩定性可以近似處理為平板穩定性問題。將兩環肋間的薄壁部分展開為一平面板，由試驗結果統計獲得，對于環向肋加強結構取0.9，則可以通過上式確定兩環向加強結構的最大間距：

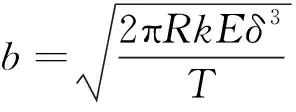
(8)

通過計算殼體總高與環向肋最大間隔的倍數，確定當前設計方案中需要引入的環向肋數目：

(9)

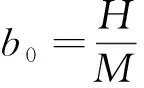
(10)

通過間距確定環向肋加強的位置：

=，=0,1,2,…,

(11)

(2)環向肋寬度確定

軸向載荷下環向肋加強結構的總載荷與光殼結構的總載荷計算公式：

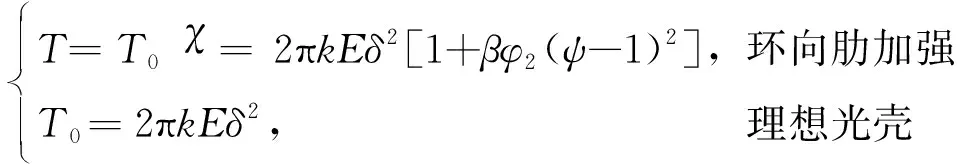
(12)

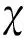
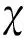
(13)

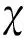
殼的環向加勁系數為：

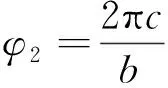
(14)

式中：為環向肋寬度；為兩環向肋間距，對應的空間位置如圖4所示。依據文獻[13]中給出的實驗數據點進行線性擬合可以得到用表示的，則項可表示為：

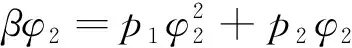
(15)

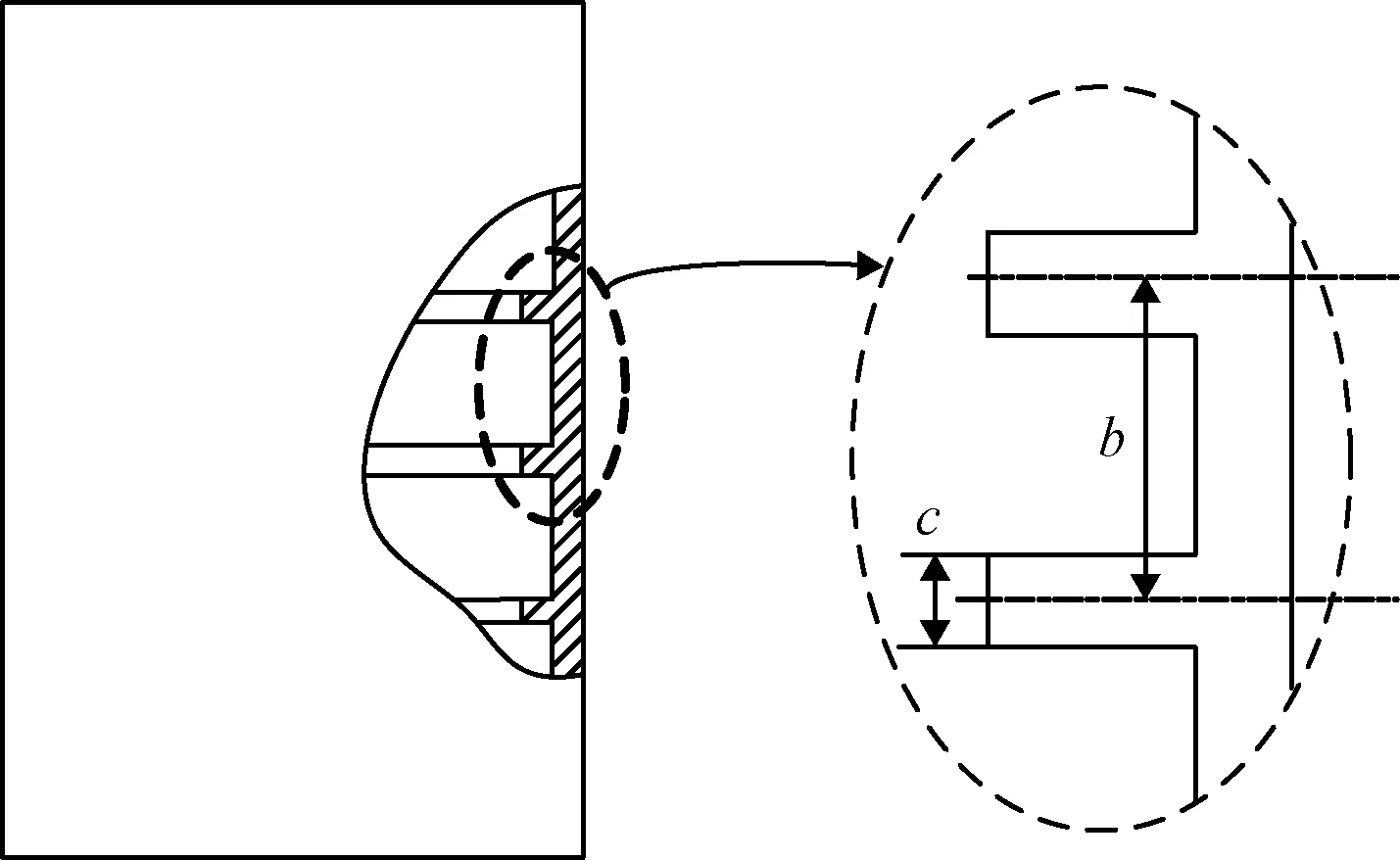
圖4 環向肋間距與肋寬示意Fig.4 Illustration of spacing distance and width of circumferential rib

式中：,為線性擬合后的擬合系數，該式為二次函數，由其特性可知在可行域內必然存在唯一極值，記該值為2，將該結果代入式(14)，得到能夠提供最大穩定性增強效果的環向肋寬度：

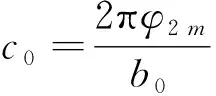
(16)

至此，需要添加的環向肋已被完全確定。這些環向結構與剛度優化后得到的縱向結構可以相互形成類似網格加強的結構，進一步提升結構的承載能力，保證該穩定性補償策略的有效性。

3.2 修正設計變量空間

將位于環向肋體積范圍內的單元剔除出優化設計空間，其單元相對密度恒為1，這樣不需要其他復雜的約束條件即可保證組成環向肋的單元在優化過程中一直存在，達到在有限單元模型中等效添加環向肋的目的。本小節將給出確定組成環向肋單元的方法。

由于環向肋為定截面形式，通過指定環向肋的添加位置和縱向寬度(坐標)范圍即可確定環向肋的體積范圍。

1)確定環向肋基準單元的位置

由于有限單元的離散性，加肋位置與單元位置必然存在誤差。本文以單層實體單元作為環向肋定位基礎單元，認為當某一層單元的縱向坐標與加肋位置之間滿足式(17)即可作為待定的基礎單元。

|-|≤05

(17)

式中：為對應第個單元的坐標；為某一環向肋的理論位置；為單元的高度。

在添加環向肋加強的位置處，基準單元的縱向坐標存在單元中心位置距離環向肋位置小于或等于半個單元縱向高度的兩種情況。

在小于半個高度的情況下，存在唯一確定的符合要求的單元縱向()坐標，即可作為第個環向肋的基準單元位置；在等于半個高度的情況下，存在兩種符合要求的單元縱向坐標,，分別位于環向肋加強位置的上下對稱兩側，取位于環向肋理論位置上方的作為確定環向肋位置的基本位置。

2)確定環向肋縱向寬度范圍內的所有單元

環向肋的寬度應當符合最大穩定性增強的寬度。有限單元模型中對模型進了離散化處理，將對應的寬度處理為單元的層數：

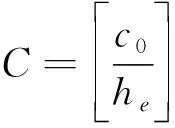
(18)

式中：為對應環向肋寬度；等效為的單元層數。

基于第個環向肋的基準單元位置與所需單元層數，得到不在環向肋體積范圍內的，組成實際設計空間的實體單元集合為：

={|≠(+)}

(19)

式中:=1,2,…,，=0,1,2,…,，為實際環向肋個數。基于第二節的分組定義，組成實際設計空間的單元組集合為：

={|used∈}

(20)

式中:=1,2,…,，=1,2,…,，為集合內元素總數。則在實際拓撲優化過程中使用的設計變量為各單元組的相對密度：

={|∈}=1,2,…,

(21)

式中:為實際使用的優化變量集合。至此完成對設計變量空間的修正。

3.3 建立拓撲優化流程

基于3.2小節所確定的修正后的設計空間，可以得到考慮穩定性的定向分組拓撲優化方法。該方法的數學模型為：

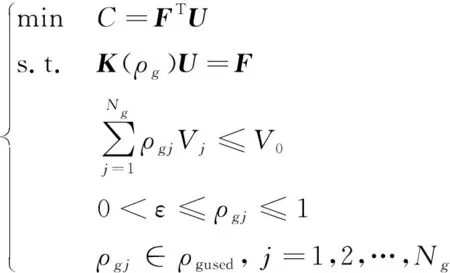
(22)

式中:各符號意義與式(2)、式(5)和式(21)相同，該模型已經使用分組定義并重新修正后的設計空間used，目標函數相對于設計變量的敏感度：

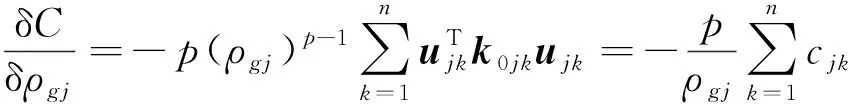
(23)

式中:,和0分別為第組中第個單元的應變能、節點位移矩陣和初始剛度矩陣，為單元組包含的單元數量，其余符號與式(21)同義。

采用最優準則法完成問題求解，環向肋增穩的定向拓撲優化方法流程如圖5所示。

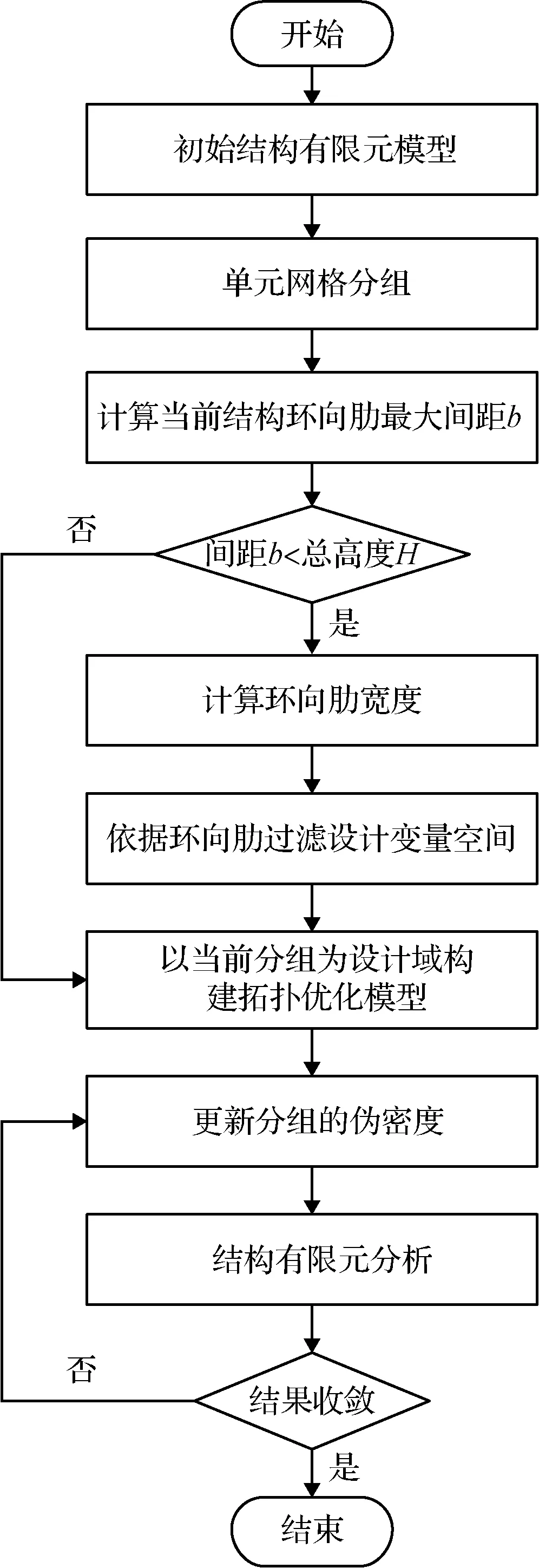
圖5 考慮穩定性的定向分組拓撲優化方法流程Fig.5 The flow of grouping oriented topology optimization method

4 算例分析

某火箭級間段為薄壁圓柱殼體加筋結構，初始設計結果如圖6所示。該級間段結構高度為720 mm，直徑為2300 mm；縱向加強筋為52條；環向肋加強肋為7條。級間段的原始結構及其蒙皮厚度、橫縱加強筋的高度與厚度如圖6所示，蒙皮厚度1.5 mm，各加強筋的高度為30 mm，縱向加強筋厚度為15 mm，環向肋的厚度為20 mm。級間段結構的殼體與縱向、橫向加強結構均使用2214牌號鋁合金，材料參數依據文獻[16]確定。該級間段設計承受載荷為總大小1800 kN的軸向力，該力均布在結構頂端,結構底端面固支約束。

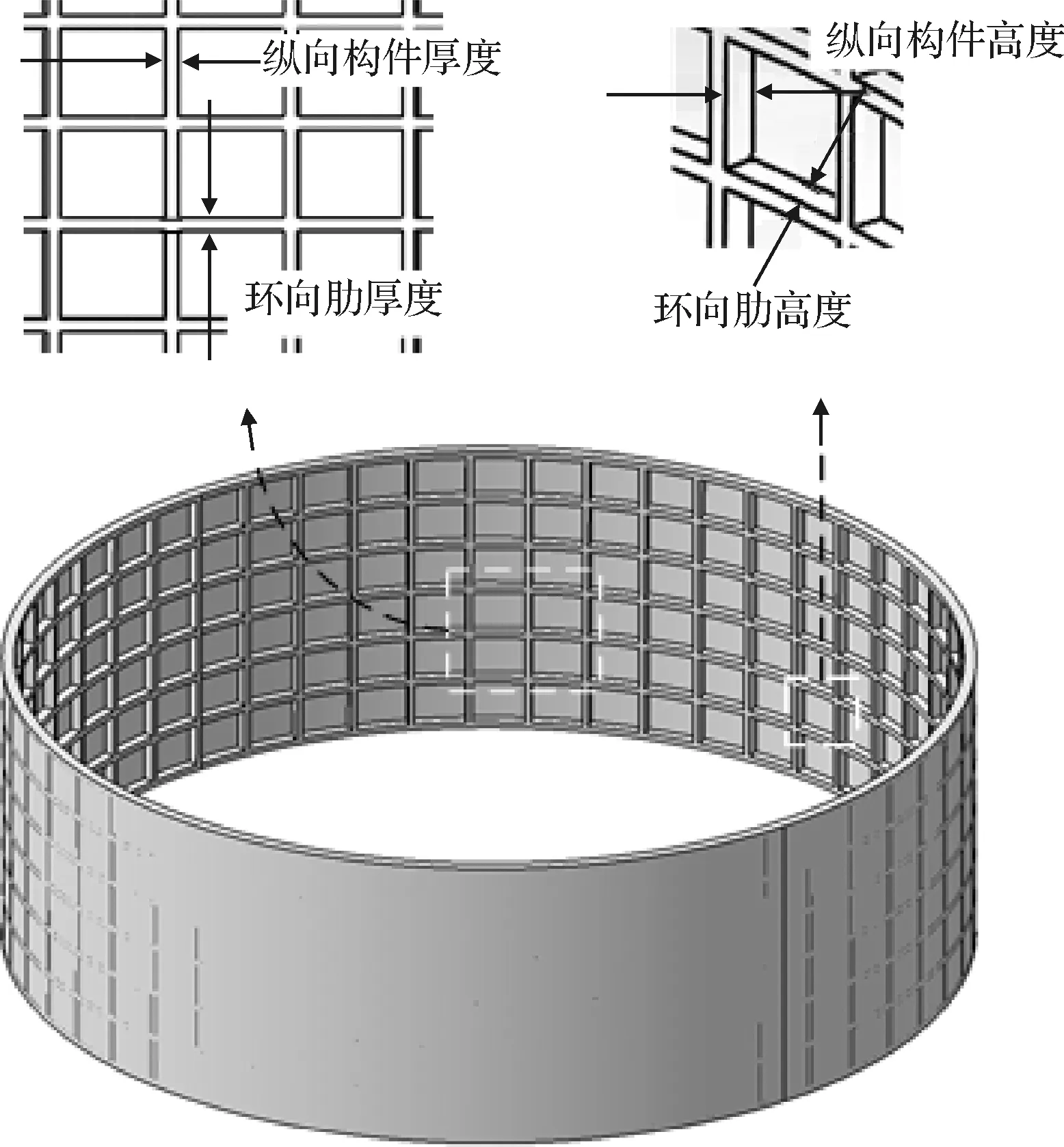
圖6 火箭級間段原始結構與相關參數定義Fig.6 Original structure of rocket Interstage and definition of related parameters

采用本文提出的方法對該級間段重新進行優化設計。以連續飽滿的薄壁圓筒結構為初始設計樣式，建立如圖7(a)所示的有限單元模型：該模型外表面為平面單元，內部為六面體實體單元，單元尺寸為10 mm，共80000個單元，81600個節點。

圖7 有限單元模型與優化結果Fig.7 Finite element model and topo-optimized result

采用3.1節的穩定性增強策略，得到肋間距應小于227.1 mm，故采用5根環向加強肋，其肋寬度為28.6 mm，布置高度分別為0、180、360、540、720 mm。對設計空間進行修正，將在環向肋體積范圍內的30400個單元剔除設計空間，保證環向肋結構在迭代過程中一直存在，得到實際拓撲優化設計空間，圖中環狀部分是不納入拓撲優化設計空間的環向肋等效單元。

使用準則優化法對該問題進行求解，經過28次迭代得到優化結果，最終確定的拓撲形式如圖7(b)所示。

由式(22)可知，該優化模型只引入了設計空間范圍的額外約束，該約束只在優化空間初始化時生效一次，不涉及后續迭代，求解效率高。模擬結構外層薄蒙皮的平面單元一直存在，與加筋設計域的實體單元共節點相連，具備模擬薄壁圓筒結構外層蒙皮和內部加強構件相互作用的能力，計算結果可信。

從獲得的拓撲優化結果形式上可以清晰地判斷出該結構具有5個環向肋和24個縱向加強構件。這些構件由于單元定向分組的原因，內部均沒有孔洞出現，邊緣與外層蒙皮垂直，符合結構的薄壁特性，具有較好的加工性。

對優化結果進行穩定性分析，失穩模式如圖8所示：

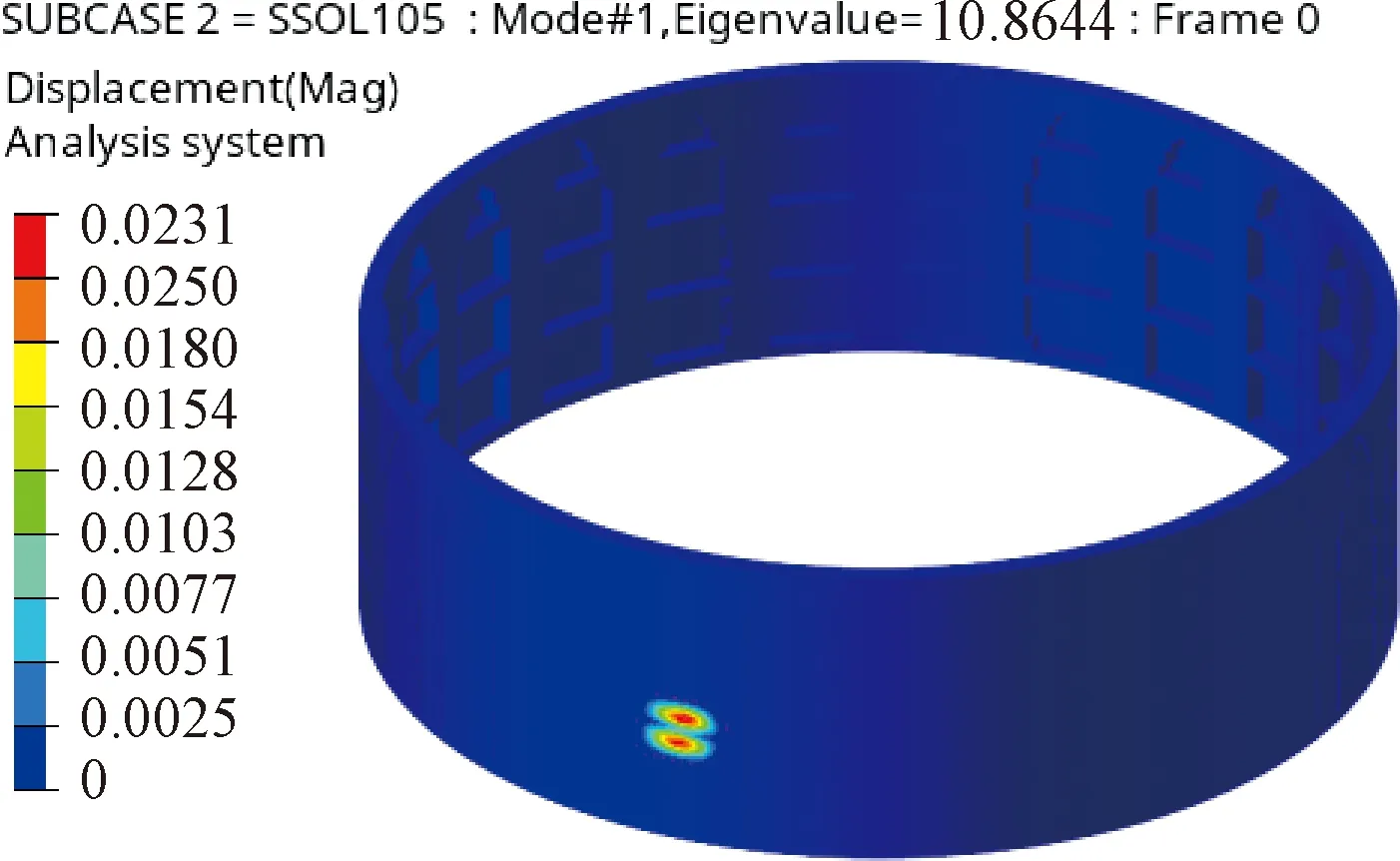
圖8 優化方案一階失穩形式Fig.8 First order buckling mode of optimized scheme

優化后方案的屈曲系數為10.86，說明優化后結構在設計載荷下不會發生失穩，穩定性較為充裕。

優化后的結構具有較好的加工性和穩定性，表明本文方法充分考慮了結構的薄壁特征，且該方法額外約束較少、計算效率高，是一種適合應用于飛行器結構總體設計階段的拓撲優化方法。

5 對比與討論

5.1 與基于經驗公式設計方法的原始結構比較

對原始方案進行穩定性分析，失穩模式如圖9所示。

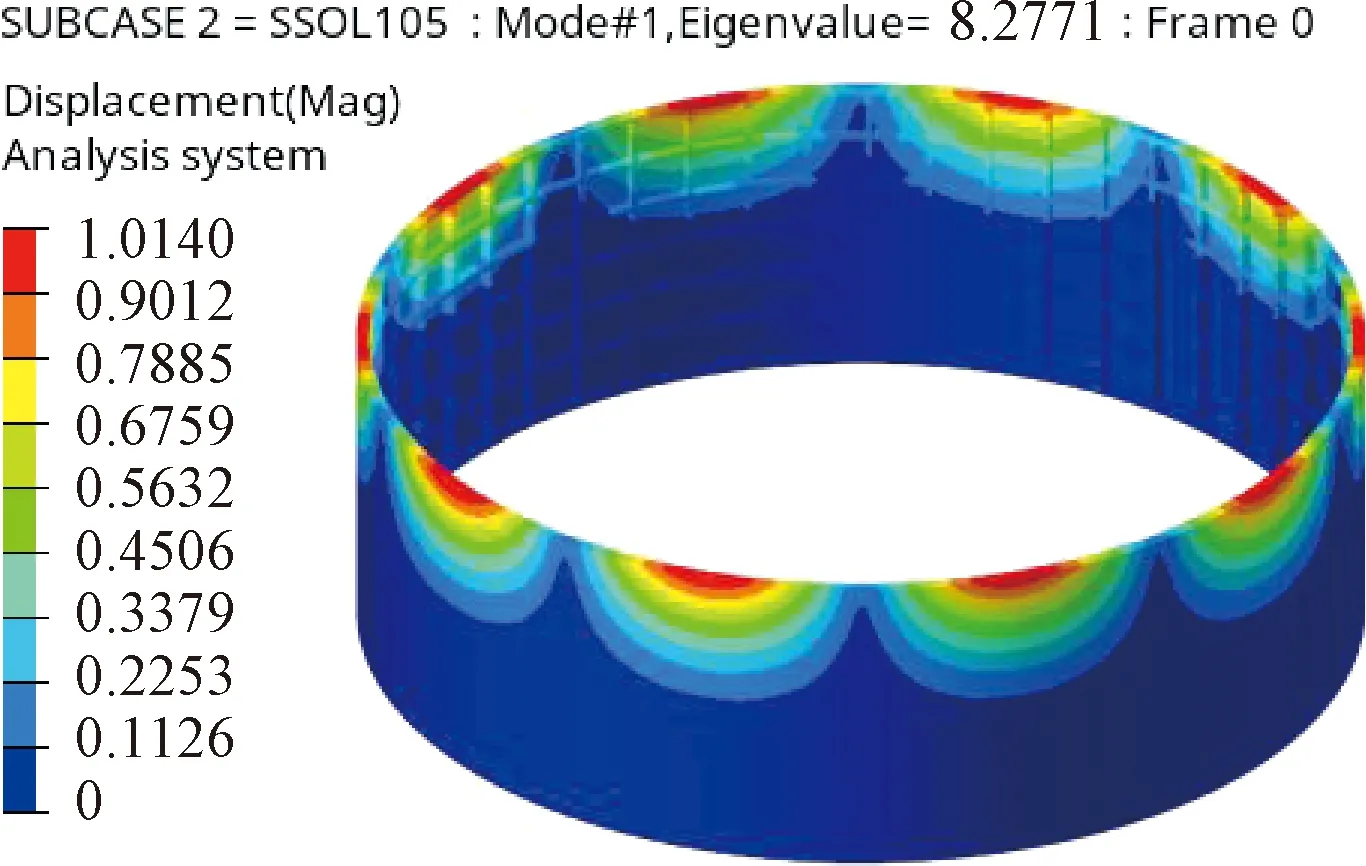
圖9 原始方案一階失穩形式Fig.9 First order buckling mode of original scheme

原始方案通過經驗公式方法計算得到加筋的數目,完成了拓撲形式的定義。該方法計算快捷，組成整體結構的各構件在初始階段就完全確定，加工性好。但是該方法的設計空間有限，不能做到沿傳力路徑的材料分布，材料利用率較低，結構質量大。

拓撲優化結果與結構原始方案相關參數對比如表1所示

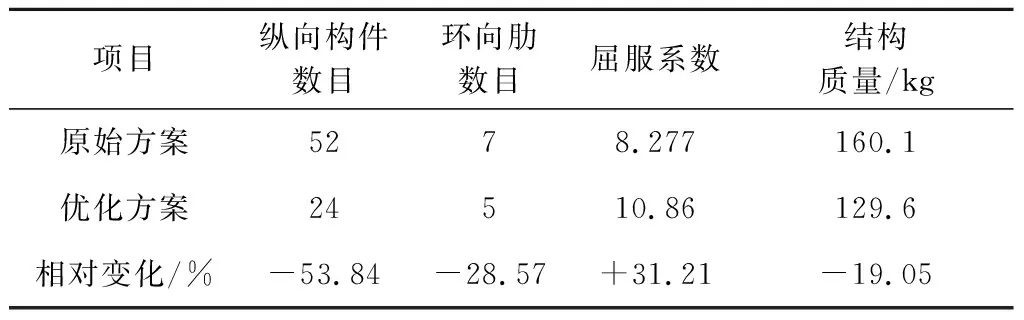
表1方案相關參數對比Table 1 Comparison of relevant parameters

相比于原始方案，優化后的結構縱向構件與環向肋數目均顯著下降，使得結構整體減重19.05%，并且能夠滿足設計指標，說明結構的材料利用效率得到了提升。

屈服系數上升31.21%。這是因為優化后結構的縱向材料沿著傳力路徑分布，分布寬度相比原始方案更大，具有更好的整體剛度，抵抗變形能力更強，使得引發結構失穩的初始形變更難產生，結構屈服系數上升。并且由于結構橫縱加強構構件數目變少，形成了單胞較大的疏網格加筋形式，結構將首先發生局部屈曲。相比于原始方案首先發生整體屈曲的情況，優化后的結構更不容易發生整體塌縮，具有更高的可靠性。

5.2 與只考慮剛度最大化優化方法比較

若只考慮剛度最大化的結構拓撲優化，將得到如不含圖7中環向肋的結果如圖10所示。該結構具有較好的加工性，質量為109.7 kg，結構屈服系數為9.879。

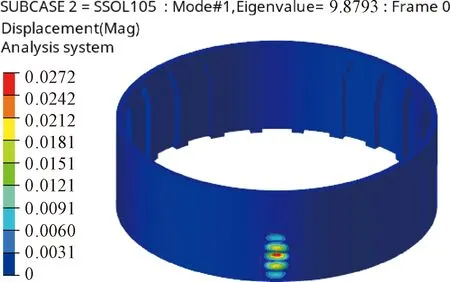
圖10 優化后結構的一階失穩模態(最大剛度方法)Fig.10 First order buckling mode of optimized scheme (max stiffness)

相比于第四節的計算結果，結構屈服系數下降9.03%，質量下降15.35%。這種變化表明：本文方法通過添加環向肋，以多付出15%的質量換取10%的穩定性補償。雖然質量上增加了20 kg，但考慮到結構本身承受的設計載荷較大，在穩定性上的補償最終表現為承載能力提升近180 kN，這種穩定性增加所帶來整體性能提升相比于減重效果更加優越。并且由于沒有添加環向肋，結構外層薄蒙皮被分為了較大縱向區域。該區域發生屈曲時雖然也是局部屈曲，但是形式相比第四節中的結果更加嚴重。

因此本文方法對結構性能的綜合提升優于只考慮剛度最大化的優化方法。

5.3 與只考慮穩定性最大化的優化方法比較

Altair公司的optistruct結構優化求解器具有穩定可靠的求解算法，優化能力已經得到多方認可。本小節將對圖7(a)所示的有限元模型使用optistruct軟件進行只考慮穩定性最大化的拓撲優化。

拓撲優化后的結構形式如圖11所示，可以確認大致存在5個縱向加強構件。這些構件材料分布的形式破碎，難以按照結果進行制造，可加工性很差。

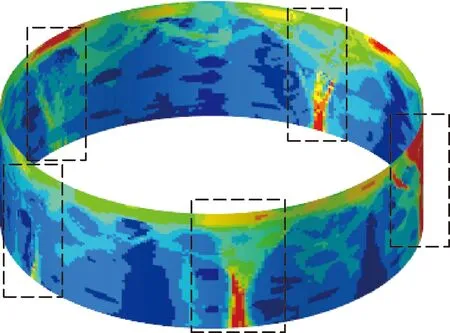
圖11 優化后的結構形式Fig.11 The form of optimized structure

該結構對應的一階失穩模態如圖12所示，屈服系數為6.177，相比于原始結構和本文方法分別下降了25.37%和43.12%。這是由于這種方法沒有考慮結構剛度，導致材料趨向結構失穩波形的樣式分布，而不沿著傳力路徑分布。這樣得到的結構抵抗變形能力較差，載荷作用下容易發生較大擾動引發屈曲，導致穩定性系數較低。

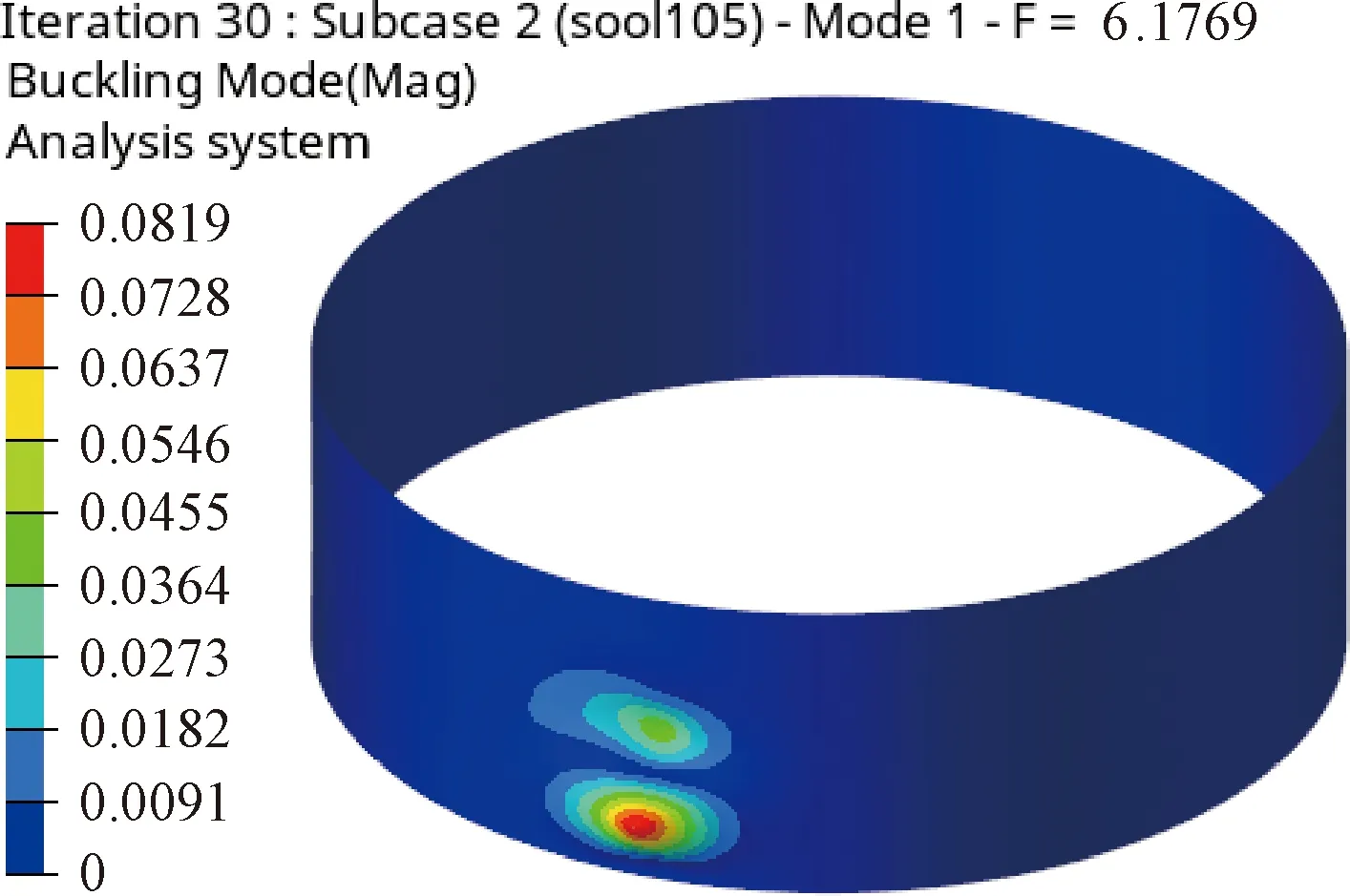
圖12 優化后結構的一階失穩模態(最大穩定性方法)Fig.12 First order buckling mode of optimized scheme (max stability)

因此本文方法在優化后結構的加工性和穩定性方面都更具優勢。

同時應注意到本文關于穩定性方面的計算采用使用于理想殼體和理想平板的經驗公式(7)，直接用于加筋薄壁結構的計算會造成穩定性設計余量較大的問題。這種非穩定性最優的考慮會導致結構增重，但本文針對的是處于飛行器總體設計階段的結構快速迭代問題，該階段可知的載荷工況較少，設計結果會作為結構詳細設計階段的輸入。相對較大的穩定性系數能夠保證結構在面對一些突發干擾和初始設計階段未曾考慮過的工況下正常工作，并且會給結構詳細設計階段提供更大的設計空間，便于進行結構精細化設計。相比于嚴格的穩定性系數邊界約束，這種考慮穩定性的方式會帶來更大的工程收益，實用性更高。

綜上，相比于幾種傳統的設計方法，本文提出的方法能夠更好地考慮薄壁結構的加工性與穩定性，得到綜合性能更優的設計方案。

6 結 論

本文針對在結構總體設計階段對飛行器艙段常用的薄壁圓筒結構進行拓撲優化時未考慮結構薄壁特性導致優化結果實用性欠佳的問題，提出了一種適用于飛行器總體設計階段的環向肋增穩定向分組拓撲優化方法。該方法主要有兩點改進：

1)通過采用定向分組的方法重新定義傳統拓撲優化方法的設計變量，保證拓撲優化結果形式符合薄壁結構的加工特點。

2)引入穩定性增強策略，通過修正設計空間范圍的方法等效添加環向肋，在不增加計算復雜度的基礎上增強了結構的穩定性。

文中給出的仿真實例說明了該方法的有效性，后續研究中將依據優化后的加強筋殼體，進一步計算環向加強筋分布，進行參數優化，通過拓撲-參數的組合優化以獲取性能更加優秀的結構，并嘗試將該方法拓展至非對稱性薄壁結構。