基于分布式剪刀構型控制力矩陀螺的大尺寸空間結構振動抑制

郭川東，胡 權，方麗萍，張景瑞，張 軍，李公軍

(1. 北京理工大學宇航學院，北京 100081；2. 北京控制工程研究所，北京 100094)

0 引 言

隨著對高功率通信和高分辨率觀測等航天任務需求的提升，航天器的太陽翼、天線、桁架機構等柔性部件的尺寸已經由十米量級向幾十米、甚至上百米量級發展。柔性部件在受外部擾動或進行姿態機動時容易產生振動，進而可能對高精度航天任務產生影響，因此需要對此類柔性部件進行主動振動抑制。傳統的集中式控制策略采取在中心剛體上安裝執行機構、利用中心剛體與柔性部件的剛柔耦合作用實現柔性結構振動抑制；或在柔性部件根部安裝阻尼器，降低結構振動對本體姿態運動的影響。但隨著航天器尺寸增大，柔性結構甚至成為系統主體，傳統的集中式控制策略已經很難實現對此類大尺度柔性航天器的姿態控制和振動抑制，則必須采用分布式控制策略，在航天器上分布式安裝執行機構和傳感器。

角動量交換裝置由于輸出力矩精確、連續且不消耗推進劑，被廣泛用于柔性航天器結構振動抑制。D’Eleuterio和Hughes首先提出在柔性結構上連續分布角動量交換裝置來實現振動抑制和形狀控制，即得到陀螺柔性體。Damaren和D’Eleute-rio最早研究了陀螺柔性體的最優控制問題及能控性和能觀性問題。Shi和Damaren研究了在固支邊界條件的柔性板末端安裝單個CMG，基于Lyapunov方法設計了框架角的控制律，主動增加結構阻尼以快速衰減振動。Hu等假設在柔性結構上分布安裝CMG，在考慮CMG動力學特性的前提下，建立了陀螺柔性體的動力學模型，并進行了陀螺柔性體的姿態控制和振動抑制。Guo等在柔性航天器上分布安裝CMG，提出了一種新的基于模態力補償器的姿態機動控制策略，抑制了撓性航天器姿態機動時的振動。賈世元等基于最優控制理論，使用遺傳算法求解了CMG在約束邊界柔性結構上的優化配置問題。但是，上述研究均基于較為理想的假設，并未考慮在工程中使用CMG的一些約束，例如，目前得到的CMG操縱律大都為魯棒偽逆操縱律，在應用中會引入誤差，且求解時計算量較大，會造成控制閉環中的延遲，降低振動抑制效果。

剪刀構型CMG廣泛應用于航天器姿態控制及柔性結構振動抑制,由一對同步進動的CMG組成，其輸出力矩方向恒定。Yang和Chang在空間桁架上安裝一對剪刀構型CMG，桁架一端可繞固定轉軸機動，另一端載有貨物或航天員，通過設計雙陀螺系統運動同步的自適應控制策略實現了桁架大范圍機動。Zhou等針對上述系統，基于Lyapunov方法設計了一種自適應非線性反饋控制器，通過實現剪刀構型CMG同步驅動完成桁架機動。為了提高高超聲速滑翔飛行器的突防能力，Zhao等提出了一種采用剪式控制力矩陀螺的機動控制方法，并設計了基于反饋線性化和線性二次型最優算法的解耦控制器。Jin將剪刀構型CMG安裝在柔性桁架端部，設計一種改進的PD控制器實現桁架機動，同時利用自適應反饋非線性控制策略實現桁架主動振動抑制。目前在公開文獻中，尚未見到使用微型剪刀構型CMG實現大型結構振動抑制方面的工作。注意到其構型簡單、操縱律易設計，本文深入研究基于該構型CMG的大尺寸空間結構振動抑制，重點分析剪刀構型CMG出現的一種“死區”現象，并設計易于工程應用的操縱律。

本文章節安排如下：第1節將建立分布式安裝有剪刀構型CMG的約束邊界柔性結構的動力學模型；第2節將基于Lyapunov方法設計剪刀構型CMG的操縱律，以期實現柔性結構振動抑制；第3節對所設計操縱律進行分析和改進；第4節通過數值算例驗證改進的剪刀構型CMG操縱律；最后，第5節將對全文作總結。

1 系統模型

具體研究對象為分布式安裝有多組剪刀構型CMG的約束邊界柔性結構，同組兩個CMG安裝在同一個平面內，其轉子轉速和框架轉向正方向如圖1所示。系統的連體坐標系為，分布安裝的第組剪刀構型CMG安裝平面坐標系定義為p;每組兩個CMG完全相同，分別編號為,a和,b，CMG框架坐標系g,a,g,b和轉子坐標系r,a,r,b原點均位于節點g。

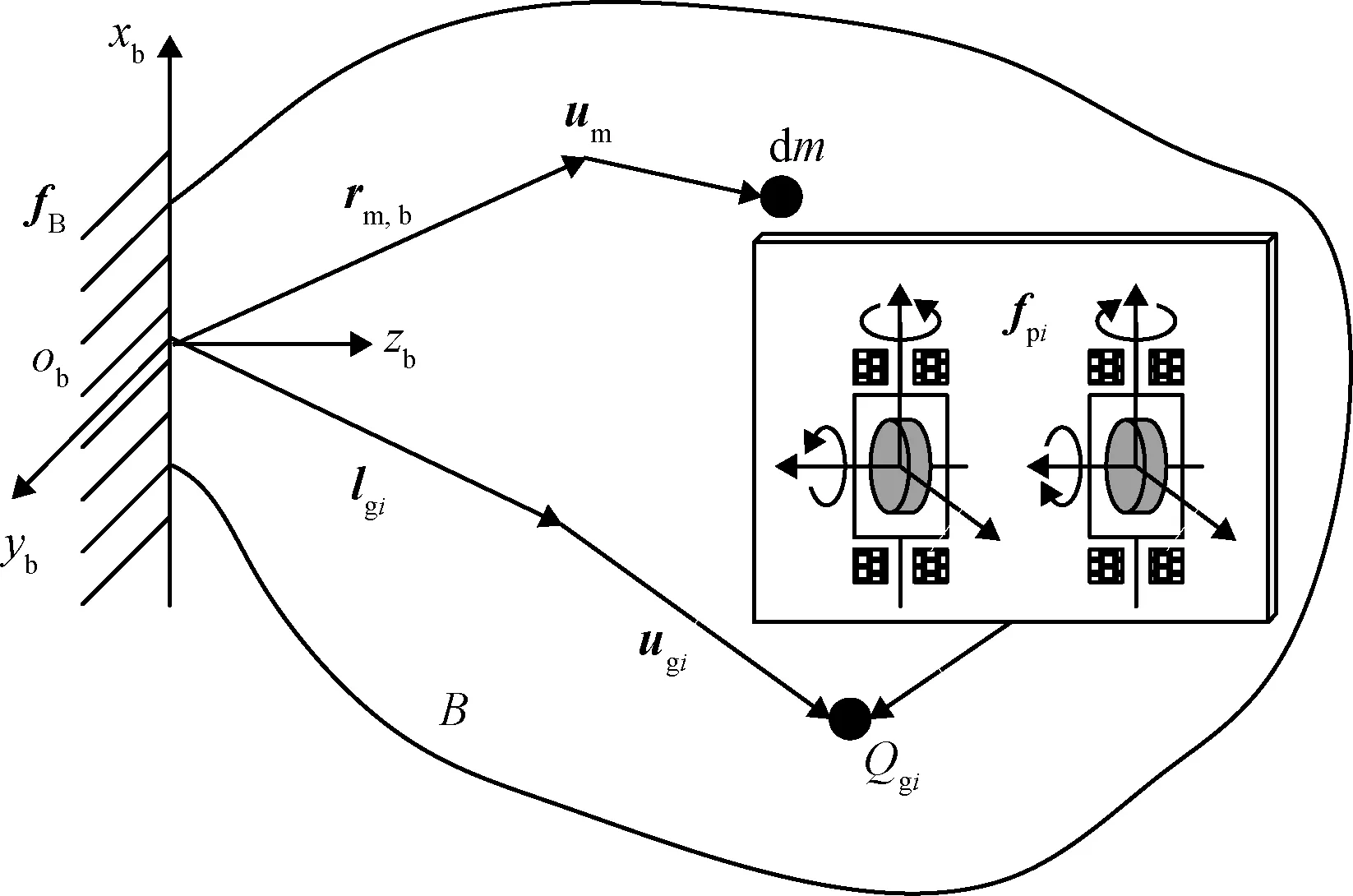
圖1 安裝有剪刀構型CMG的柔性結構示意圖Fig.1 Flexible structure with distributed V-gimbaled CMGs

1.1 剪刀構型CMG

如圖2所示，當剪刀構型CMG輸出力矩時，每個CMG的框架和轉子均轉向相反、轉速相等，則兩個CMG的力矩值分別為

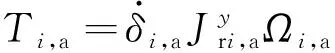
(1)

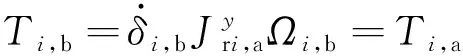
(2)

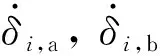
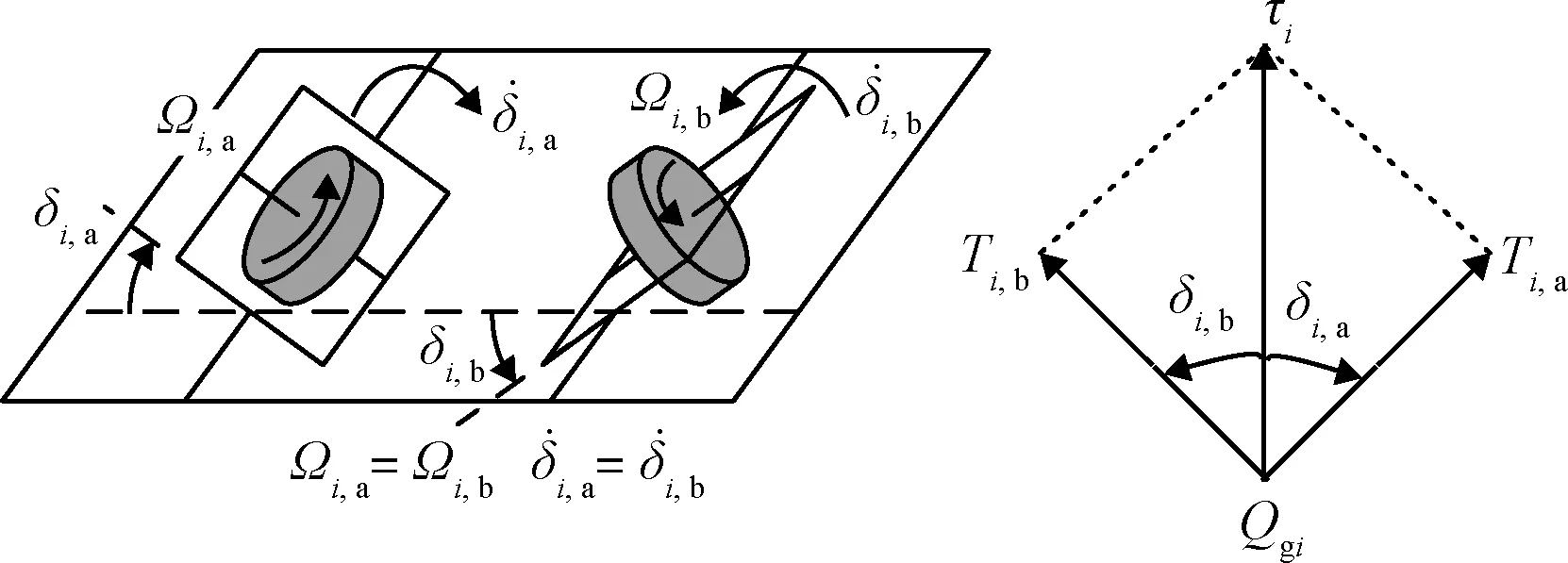
圖2 剪刀構型CMG示意圖Fig.2 Sketch of V-gimbaled CMGs

容易看出，合力矩的方向垂直圖2所示安裝平面，其值有

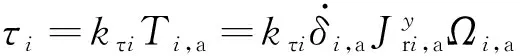
(3)

式中：為變系數，其值有

=2cos,a

(4)

式中：,a為第組剪刀構型CMG中第個CMG轉過的框架角，,a∈[-180°,180°)。在框架角小角度運動假設下，可近似認為=2或=-2。由式(4)易得

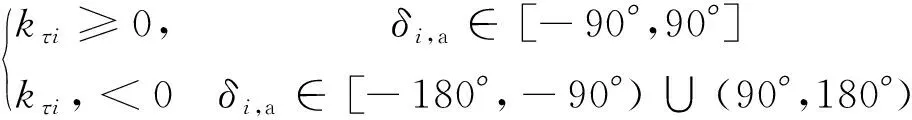
(5)

1.2 動力學模型

在文獻[11]和[21]中，Hu等在考慮CMG動力學特性以及CMG與柔性結構之間的相互作用情形下，推導了該系統的動力學方程。在假設柔性結構發生小范圍彈性變形的假設條件下，其上質量微元d相對于的彈性變形和彈性轉角采用模態展開法描述，

=

(6)

=

(7)

式中：∈3×,∈3×分別是d的平動模態向量和轉動模態向量；∈×1為柔性結構的模態坐標，為用于描述柔性結構彈性變形的模態階數。

由于研究對象為約束邊界柔性結構，因此只需要考慮柔性結構的振動方程。基于文獻[11]中式(7)，消去方程組的高階非線性項，并保留了CMG與柔性結構之間的相互作用，得到結構振動方程為

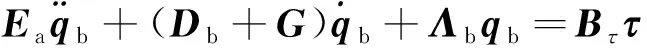
(8)

式中：∈×是一個對稱矩陣，表示受CMG影響的柔性結構模態質量矩陣；∈×和∈×為對角矩陣，分別表示柔性結構本身的阻尼矩陣和剛度矩陣；∈×是一個反對稱矩陣，表示CMG與柔性結構的耦合系數矩陣；是由CMG的框架轉動所產生的作用于柔性結構的廣義模態力，是CMG的力矩系數矩陣；=[,…,]，其中是第組剪刀構型CMG的輸出力矩。

這里變量,和由以下公式給出，

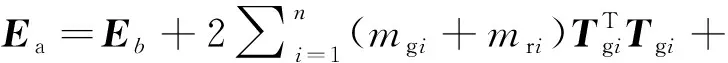
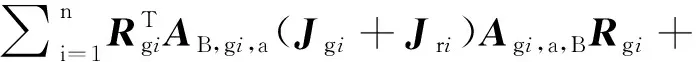
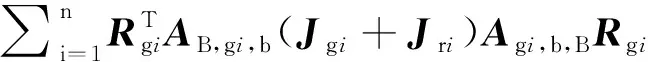
(9)

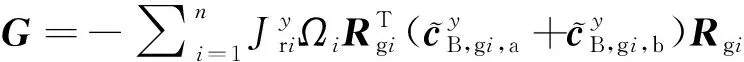
(10)

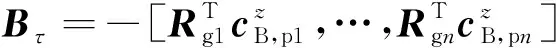
(11)

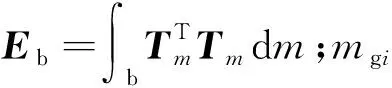
假設在柔性結構上共位安裝組剪刀構型CMG和角速度計，選取為第組剪刀構型CMG力矩輸出方向上的分量，由微機電系統(MEMS)角速度計測得，即有

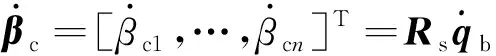
(12)

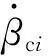
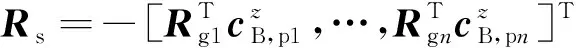
(13)

對比式(1)與式(13)可以看出，

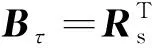
(14)

從式(8)可以直觀看出，當需要抑制柔性結構的階振動時，需要使用的剪刀構型CMG的數量應滿足≥。當需要抑制的模態階數較多時，所需要的CMG的數量也隨之增加。利用剪刀構型CMG開展柔性結構振動抑制，適合于長桿、帆板、桁架等較為簡單的柔性結構。

2 剪刀構型CMG操縱律設計

基于上一節的系統動力學模型，選取Lyapunov函數，

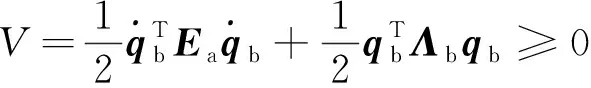
(15)

對其求導有，

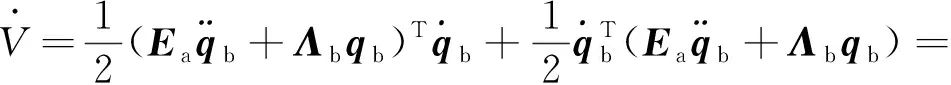
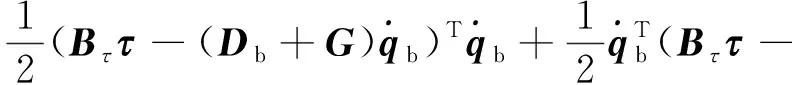
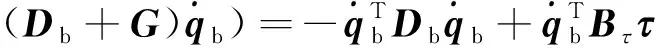
(16)

在第二步利用了的反對稱性。設計角速度反饋控制律為

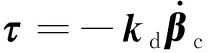
(17)

式中：=diag(,…,d),d>0，則有

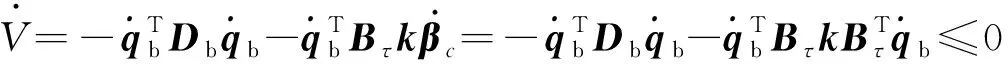
(18)

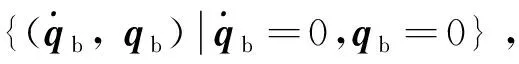
由式(17)即有，對第組剪刀構型CMG有

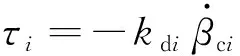
(19)

將式(3)代入式(19)可得

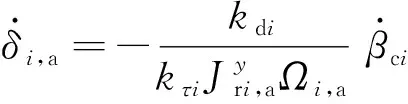
(20)

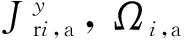
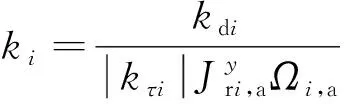
(21)

即有>0，結合式(5)，則CMG操縱律修正為

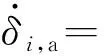
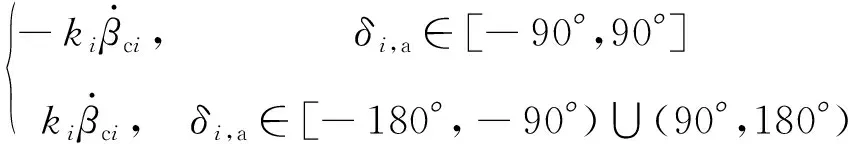
(22)

由于兩個CMG的框架轉向相反、轉速相等，則有

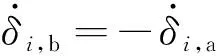
(23)

至此已經得到了在約束邊界柔性結構上分布安裝組剪刀構型CMG時，實現柔性結構振動抑制的剪刀構型CMG的操縱律。只需選取適當的反饋增益>0，即可保證系統的漸近穩定性。

3 操縱律分析及其改進

3.1 操縱律分析

以10 m長的柔性桁架為仿真對象，桁架質量為11.49 kg，基頻為1.8238 Hz。在桁架端部安裝兩組剪刀構型CMG，如圖3所示，兩組剪刀構型CMG輸出力矩均在桁架本體系的方向上。第一組剪刀構型CMG安裝在桁架端部，用于演示式(22)和(23)所示操縱律,抑制桁架在方向上的振動；第二組剪刀構型CMG安裝在距離桁架端部0.5 m處，用于激勵方向上的振動，單個CMG的質量約1.25 kg、轉子角動量為0.3 N·m·s，框架角速度最大幅值為90(°)·s。不考慮CMG內部的摩擦和力矩“死區”等問題。掛載CMG后桁架基頻降低至1.1459 Hz。

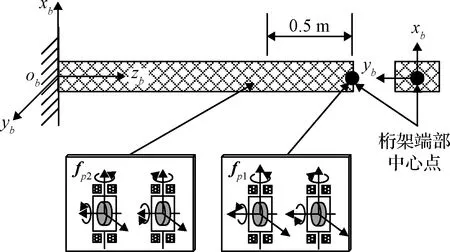
圖3 CMG安裝示意圖Fig.3 Sketch of V-gimbaled CMGs locations

第二組剪刀構型CMG驅動采用正弦激勵規律，即

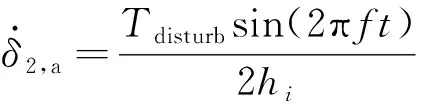
(24)

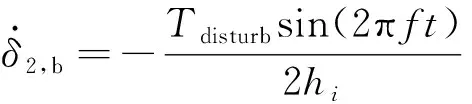
(25)

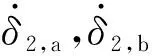
在仿真中，前10 s對桁架施加激勵，不施加主動控制，此時參數選擇為=01 N·m,=116 Hz；10 s后激勵結束，采用式(22)和(23)的操縱律開始施加主動振動抑制，設置控制增益=800。為了避免框架軸電機長期高速驅動，設定框架軸的最高轉速為57.3(°)·s。在工程試驗過程中，CMG按設定的操縱律工作，發現在試驗最開始的一小段時間內，CMG存在啟動延遲。為了考察CMG在較為極端情況下的工作能力，并重現工程試驗中的啟動延遲現象，在操縱律分析過程中,假設初始時第一組剪刀構型CMG工作在“零力矩”狀態，即=90°,=-90°。

桁架端部中心點位置如圖3所示，以桁架端部中心點在桁架本體坐標系下的變形作為考察桁架變形量的依據。經過20 s仿真，得到桁架端部中心點的變形情況,如圖4所示。可以看出，自第10 s振動抑制開始后，端部中心點變形并沒有按期望變小，而是出現了異常的增大；桁架振動抑制的效果并不明顯。

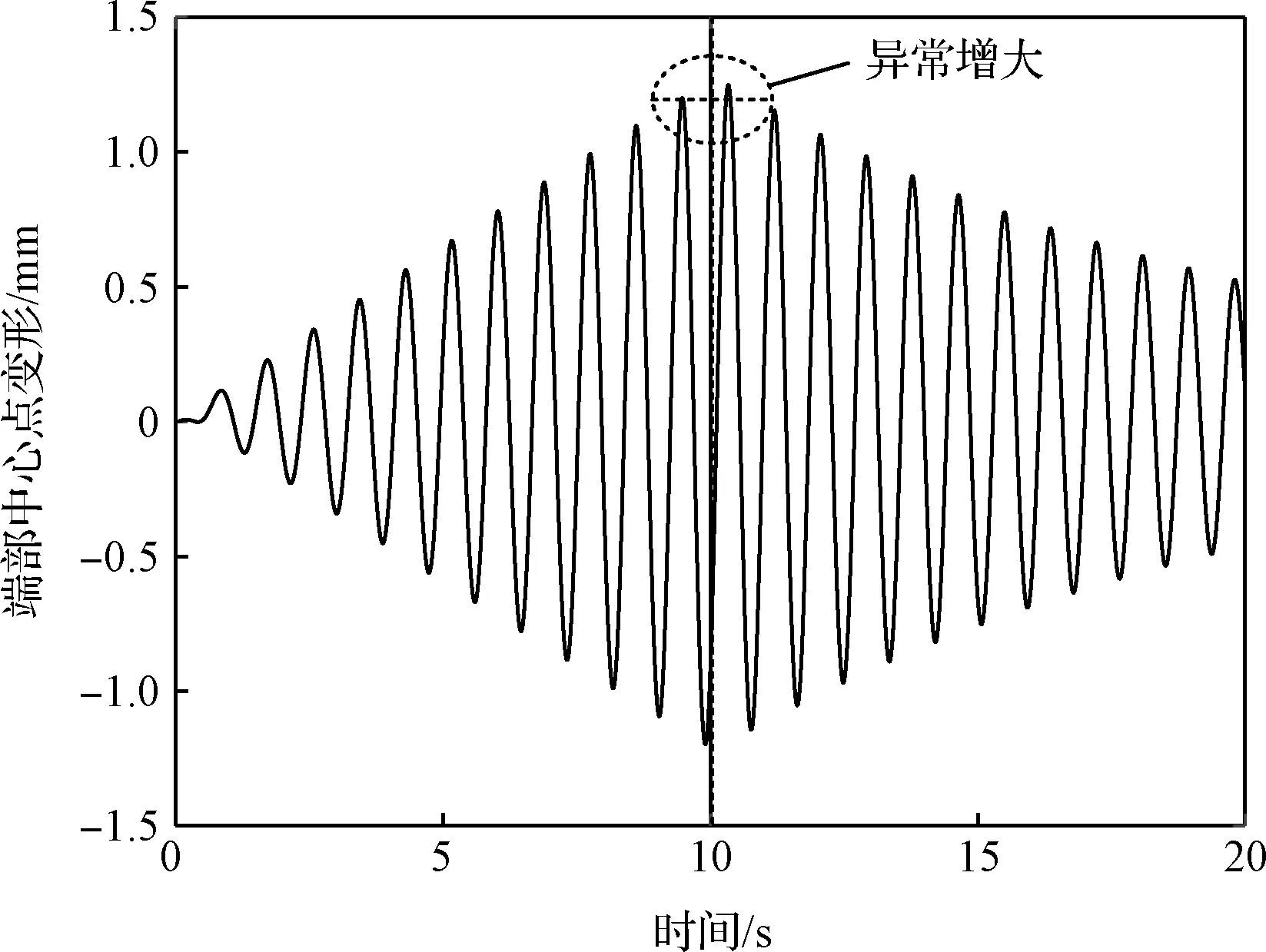
圖4 桁架端部中心點變形(振動抑制效果不明顯)Fig.4 The deformation of the center point on the end of the truss (poor vibration suppression effectiveness)

第一組剪刀構型CMG框架軸運動規律如圖5所示，可以看出，在10 s～10.3 s，短短0.3 s時間內，框架軸運動方向進行了數十次切換，進入一種類似“死區”的狀態。這種短時間內的密集切換，在工程上難以實現，也是在工程試驗過程中出現CMG啟動延遲的原因。在工程試驗過程中，這種情況持續的時間會更長，嚴重影響振動抑制的效果。

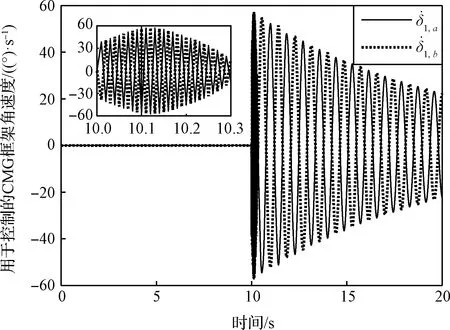
圖5 第一組CMG框架角速度(振動抑制效果不明顯)Fig.5 The gimbal angular velocity of the first pair of CMGs used for vibration suppression (poor vibration suppression effectiveness)

為深入分析“死區”產生的原因，繪制10 s后第一組剪刀構型CMG安裝位置處MEMS角速度計測量值、第一組剪刀構型CMG中號CMG的框架角速度以及號CMG的框架角度的三維曲線，如圖6所示。圖中深色曲線(黑色虛線框圈出)為“死區”狀態下的曲線，淺色曲線(右上)為CMG正常工作時的曲線。可以明顯看出，“死區”狀態出現在角速度計測量值為負值的時候，此時框架角在90°附近擺動；在“死區”狀態下，當框架角大于90°時，框架角速度為負值，此時框架角減小；當框架角減小至90°以下時，框架角速度切換為正值，此時框架角增大。框架的運動陷入“死區”循環。當角速度計測得的值轉為正值時，框架軸運動才脫離“死區”，但框架軸脫離“死區”后并未取得較好的振動抑制效果。結合式(22)可知，式(22)給出的CMG操縱律為分段函數形式，存在-90°和90°兩個分段點，“死區”出現在分段點附近。

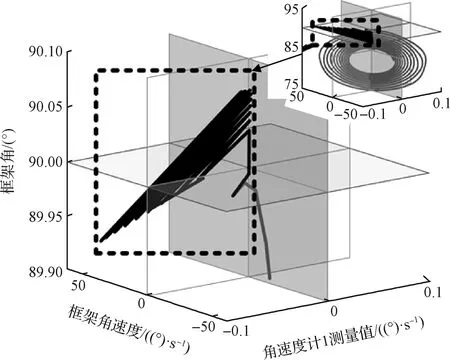
圖6 第一組CMG框架軸運動分析Fig.6 Analysis of gimbal motion of the first pair of CMGs for vibration suppression

該仿真工況較好還原了工程試驗中出現的啟動延遲現象，也能解釋啟動延遲出現的原因，有助于開展操縱律的更新設計。

3.2 避“死區”操縱律設計

為了使框架軸運動能快速轉出“死區”，對剪刀構型CMG操縱律作出調整，設計一種避“死區”操縱律,如圖7所示。

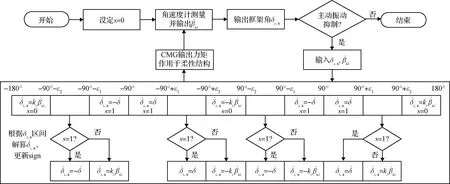
圖7 應用避“死區”操縱律實現柔性結構振動抑制流程圖Fig.7 Flow chart of vibration suppression for flexible structures by applying “dead zone avoidance” steering law

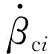
4 仿真校驗

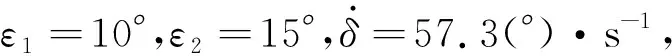
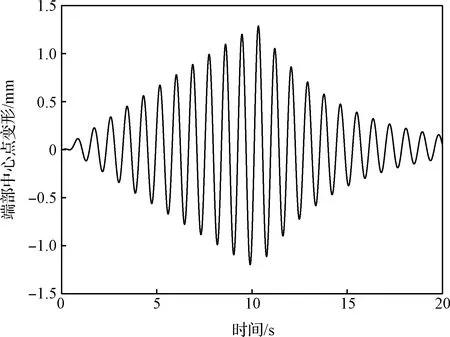
圖8 桁架端部中心點變形Fig.8 The deformation of the center point on the end of the truss

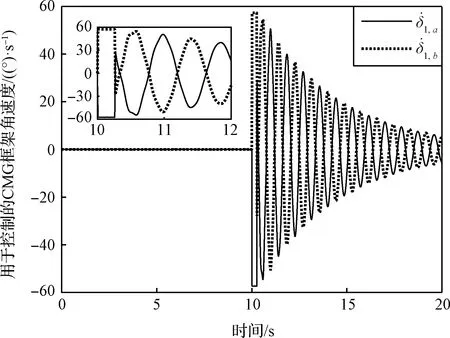
圖9 第一組CMG框架角速度Fig.9 The gimbal angular velocity of the first pair of CMGs used for vibration suppression

框架角的運動曲線如圖10所示，可以看出，振動抑制開始之后，CMG框架角快速運動到(-75°,75°)區間內，即圖7中的(-90°+,90°-)區間，實現了持續地輸出振動抑制力矩。

圖10 第一組CMG框架角運動曲線Fig.10 The gimbal angular of the first pair of CMGs used for vibration suppression

同時模擬了10 s激勵結束后不施加主動振動抑制的情形，得到不施加主動振動抑制時端部中心點變形情況如圖11所示，對比圖8施加主動振動抑制時的結果，可以看出利用剪刀構型CMG很好地實現了柔性結構的主動振動抑制。

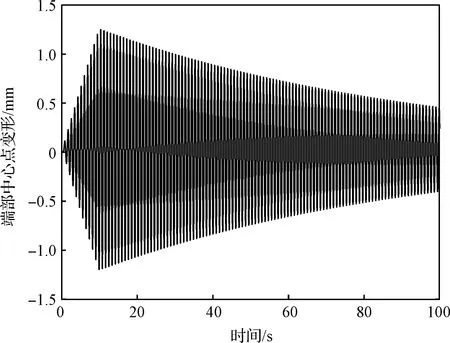
圖11 無控時桁架端部中心點變形Fig.11 The deformation of the center point on the end of the truss without active vibration suppression

5 結 論

本文以約束邊界空間柔性結構為研究對象，在結構上分布安裝剪刀構型CMG，通過建立系統動力學模型，基于Lyapunov方法設計了剪刀構型CMG的框架軸操縱律。以單部10 m長的柔性桁架為仿真對象，在桁架上安裝兩組剪刀構型CMG，一組用于激勵桁架產生振動，另一組應用所設計控制方法進行振動抑制仿真。在仿真中發現所設計的操縱律存在“死區”問題，進而改進了所設計框架軸操縱律，設計了一種可避“死區”的操縱律。仿真結果表明，所設計避“死區”操縱律可以較好實現桁架振動抑制，且改善了振動抑制的性能。

值得注意的是，在柔性結構上安裝CMG，會增加結構質量、降低結構頻率。針對這一問題，可以在兩方面開展進一步研究：一方面，研發集成化、小型化的CMG；另一方面，賦予CMG更多功能，如利用CMG內部的高速轉子進行能量存儲，同時通過CMG框架轉動輸出分布式控制力矩用于柔性結構振動抑制，從而減輕系統中能量存儲系統的質量，可進一步彌補在柔性結構上安裝CMG帶來的質量增加，同時降低對CMG微型化的要求，獲得更大的可靠性。