基于雙目手眼相機的自動化精度測試系統
唐艷慧,任 宏,劉巧元,姜金辰,王 帥,孫海江
(中國科學院長春光學精密機械與物理研究所,長春 130033)
0 引言
視覺測量技術根據相機獲取視覺測量的信息從而對目標的位置和姿態進行測量。通過相機獲得目標圖像生成匹配的像對,再利用目標在相機左右目的視差及模型參數反推其在三維坐標及位姿。相機和雙目模型就是對上述過程的數學描述。在執行空間操作任務時,首先需要獲取的就是目標航天器與服務航天器的相對位姿和運動等信息。視覺測量精度有精度高、隱蔽性強、體積小、設備相對簡單、成本低等優勢,成為首選測量方法。機器視覺因具有靈活性被廣泛應用在各種控制系統中,而視覺位姿測量作為核心的視覺技術得到廣泛關注。
近些年,航測相機在航天航空任務中占有核心地位,相機性能指標直接影響獲取信息的準確性。在航測相機研制過程中需要對其內外參進行嚴格校準,測試相機精度從而實現精確定位[1]。位姿測量精度是相機重要指標之一。現有的精度測試方法多為單點測量,不僅慢且覆蓋面小。精度測試的指標應在使用前進行嚴格檢測,保證其達到設計要求[2-3],為后續執行任務做好保障工作。本實驗提供了自動化位姿測量相機精度測試平臺,克服現有的精度測試問題,可以多點,多位移,多角度,全視場進行精度測試。且可以調節目標運動速度同時進行視覺捕捉實驗。為今后同類型的平臺提供參考價值。
1 手眼相機平臺
隨著航天、航空事業發展,機械臂成為無人機或輔助航天員出艙工作的重要設備,位姿測量手眼相機作為機械臂視覺引導,視覺伺服的重要組成部分[4-6],根據實際需求設計了手眼相機自動化精度測試系統。視覺模塊如圖1所示。
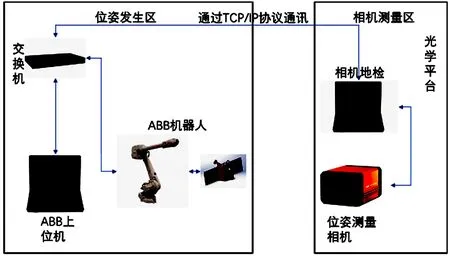
圖1 視覺模塊示意圖
工業機器人選用不確定度為15μm的IRB-2600型號的ABB工業機器人,通過上位機指令控制機械臂運動,手眼相機實際應用如圖2所示。通過上位機機械臂與相機采集的位姿互相通信,從而達到自動化測試的效果。

圖2 手眼相機實物
2 手眼相機自動化測試系統
2.1 相機標定
雙目立體視覺是基于三角原理進行三維信息的獲取,基于視差原理的一種方法。該過程可以模擬人眼的立體感知過程。目標是求出三維空間中目標物體相對于相機坐標系的三維坐標,用來進行后續的坐標變化以及機械手控制。
圖3所示為雙目立體視覺系統三維模型圖,相機左右目的投影中心連線的距離為基線,用B表示。相機左右目同時觀看物體P時在相機的成像點分別為(pleft=Xleft,Yleft);(pright=Xright,Yright)。將相機放置同一平面上,成像點P的Y軸坐標是相同的,故Yleft=Xleft=Y。由三角關系可以得到如下關系式:
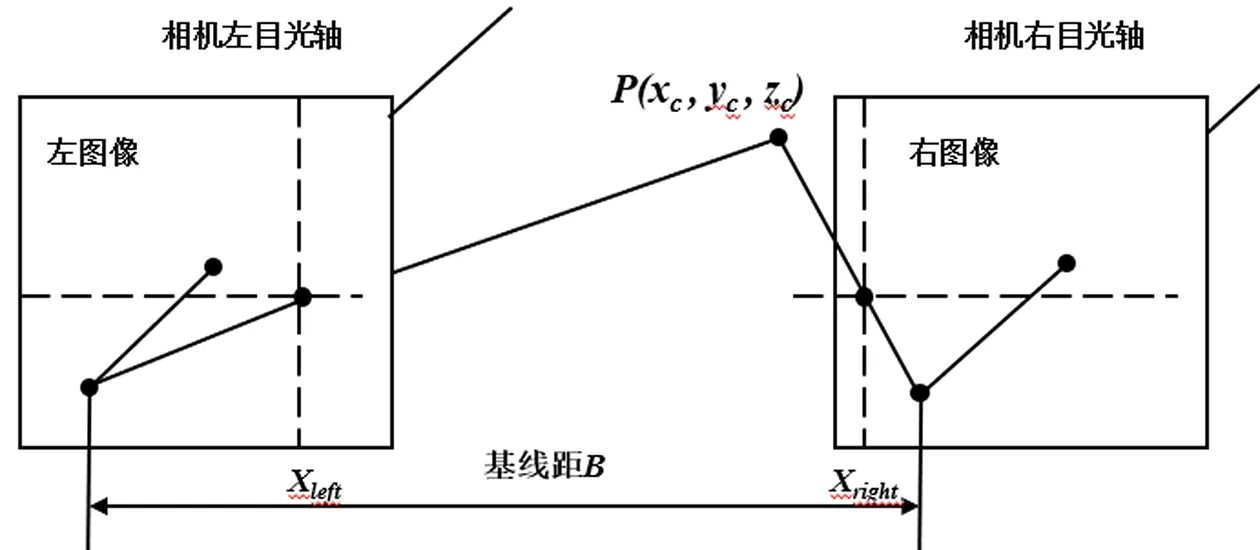
圖3 雙目立體視覺系統三維模型
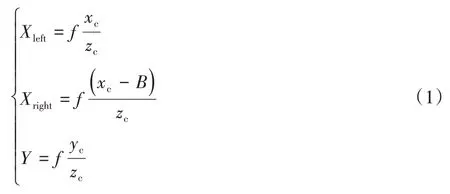
視差被定義在相同點相機左右目X軸向的偏差,即:
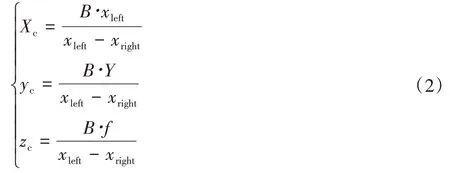
通過上式即可求出空間中任意一點三維空間中的坐標。
張正友相機標定方法選用棋盤格作為相機的標定板。在標定的過程中,假定標定棋盤格所在的平面為世界坐標系中Zw=0的平面上,將棋盤格上的某個角點設置為原點,理論上只要知道棋盤格每一個格子占據的尺寸,就能得出所有棋盤格內角點的世界坐標。同時棋盤格內角點的像素坐標可以通過圖像處理的方法計算得出,從而借助于平面單應性、非線性優化等理論求解出相機的內外參數,相機標定后得到了內參和外參進而得到了物點和像點間的映射關系,所得參數如表1所示。表中參數A表示相機的內部參數矩陣;fx、fy為像平面中的有效焦距,u0、v0為圖像的主點坐標,γ為相機的坐標軸之間的不垂直因子;k1、k2、k3、p1、p2為徑向、切向畸變參數;矩陣R和矩陣T為相機的旋轉矩陣和平移變量,表示相機左目坐標系轉換到相機右目坐標系的旋轉矩陣和平移向量。

表1 相機標定的參數
本質上來說雙目立體視覺,是相機左目和右目再看同一個目標點時,連接探測器上的像點和相機投影中心進行反投影,兩條光纖的交點位置實際就是目標的位置。
2.2 機械臂末端執行器坐標系與基座坐標系的轉換
機械臂運動的姿態一般是XYZ三軸旋轉方向,歐拉旋轉變化矩陣是由3個非交換的旋轉矩陣相乘計算,旋轉次序不同共分為12種不同類型的歐拉角。該機械臂末端執行器坐標系與基座的坐標系轉換的歐拉角順序為ZYX型,轉換的關系用旋轉矩陣R zyx(α,β,γ)表示,轉換示意圖如圖4所示。
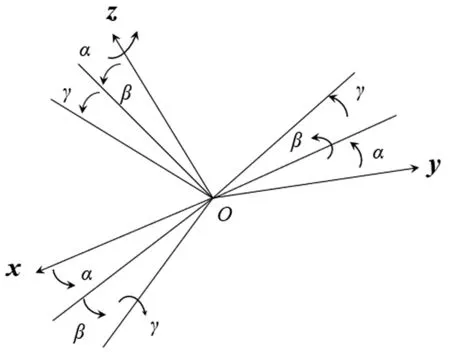
圖4 歐拉角旋轉示意圖
圖4所示為機械臂末端執行器坐標系先繞著z軸旋轉α角,再繞y軸旋轉β角,最后繞x軸旋轉γ角,得到了基座的坐標系,轉換公式為:
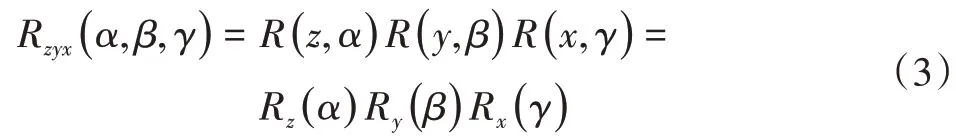
由式(3)可計算出機械臂末端執行器坐標系和基座坐標系旋轉矩陣的結果:
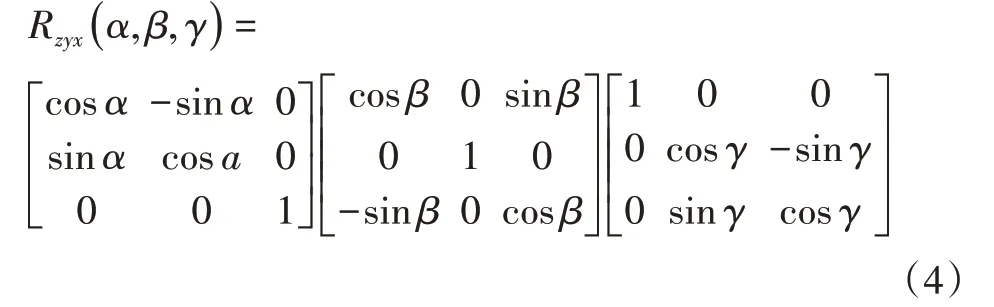
通過式(4)可知手眼相機標定前需要知道機器人坐標系旋轉矩陣的旋轉順序。
2.3 手眼相機精度測試坐標轉換關系
坐標系轉換關系如圖5所示。坐標系轉換用4×4矩陣描述,歐拉角采用ZYX順序,即旋轉矩陣R=rotz×roty×rotx。箭頭指向標識源坐標系與目的坐標系,X為法蘭坐標系和目標外部基準坐標系轉換關系,T1為關節測量臂測量目標及其工裝外部基準轉換關系,T2為相機外參,相機與相機外部基準轉換關系,T3(n)為相機輸出位姿,T4(0)為初始相機外部基準坐標系與目標外部基準坐標系轉換關系,T4(n)為相機外部基準坐標系與位移后目標外部基準坐標系轉換關系,T3'(n)為通過下式解算出相機測量目標位姿真值。
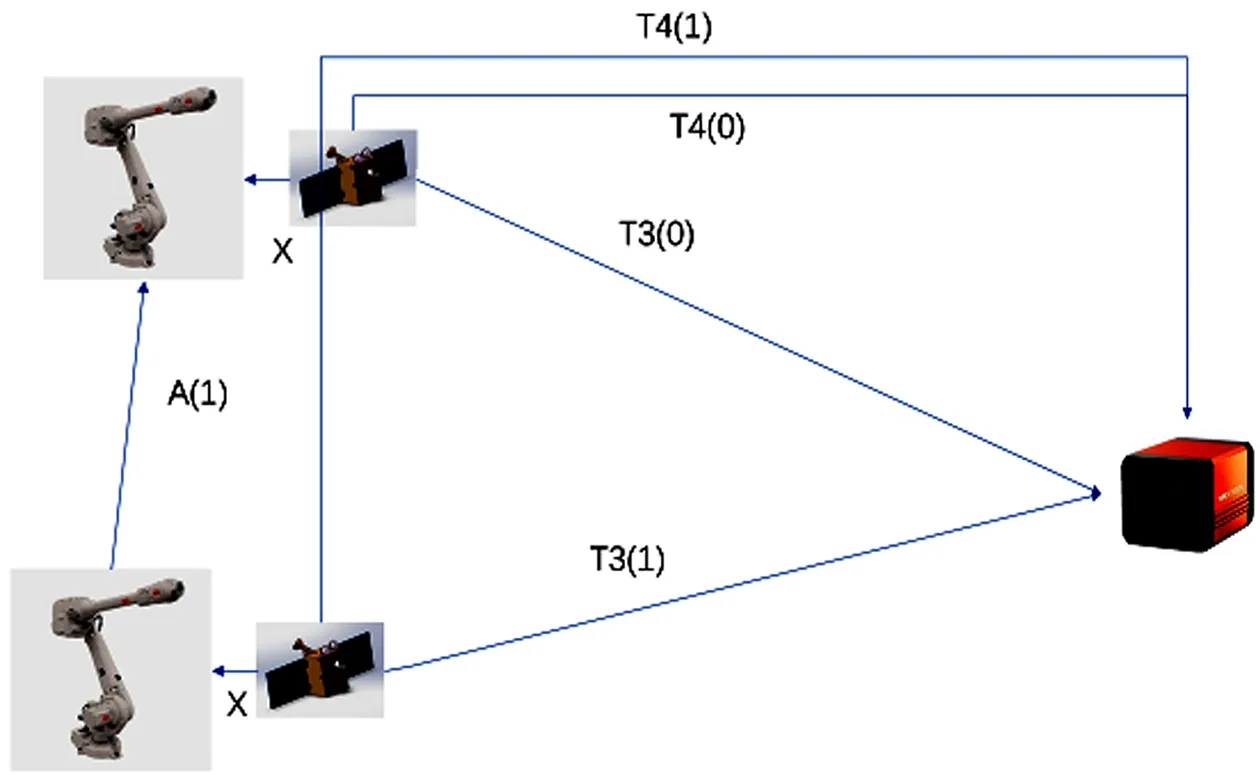
圖5 手眼相機關系轉換
以初始點為外部基準,運用Matlab隨機生成ABB運動軌跡,軌跡文件記錄軌跡點與初始點六自由度偏差A(n),上位機控制機械臂逐點運動并記錄輸出位姿T3作為測量值,外參T2作為已知量,根據下式子求解T3'(n);
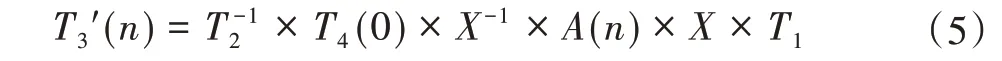
3 軟件設計實現
在vs2017作為上位機軟件開發平臺,結合C++與其他的庫函數進行控制程序的二次開發,界面如圖6所示。運用張正友標定法選用5×5的圓點標定板作為校準物體,選用圓形標定板是因為圓的確定相對精準,可以使用圓外圍的像素減少了圖像噪聲的影響。標定板上25個已知特征點如圖7所示,可以采用最小二乘法求解降低誤差的影響。本實驗搭建了自動化標定平臺,將機械臂末端法蘭上采集的標定板圖像輸入到上位機軟件中進行計算,由圖所示可以獲得相機的內參數和外參數,為后續精度測試提供保障工作。
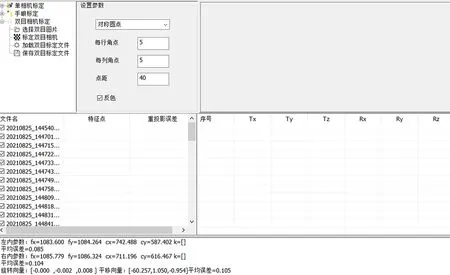
圖6 標定MFC界面

圖7 標定板
4 實驗結果及分析
手眼相機測量精度前的標定的本質是AX=XB的求解過程,在實際的應用中,A和B都會不可避免的存在誤差。對于本文研究的手眼系統,A的誤差表示機械臂的相對運動誤差,B的誤差表示相機運動的估計誤差,影響手眼相機標定方法的精度。所搭建的手眼相機自動化標定平臺測試精度結果如表2所示,RMS表示均方根,公式不再贅述。
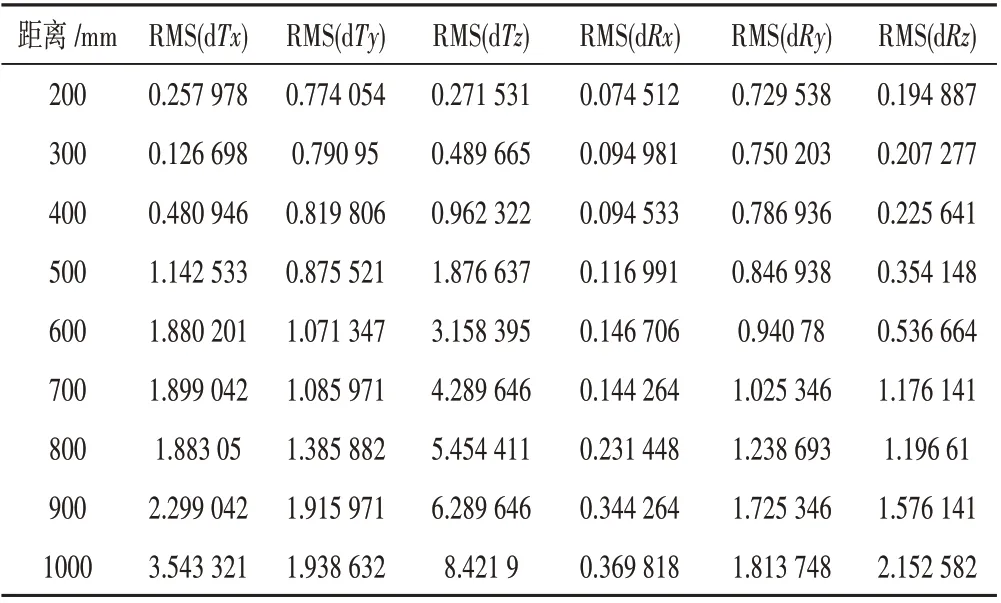
表2 雙目精度測試結果
為驗證標定的精度,將標定的結果代入相機模型進行誤差分析得到了如圖8~9的誤差分布曲線。
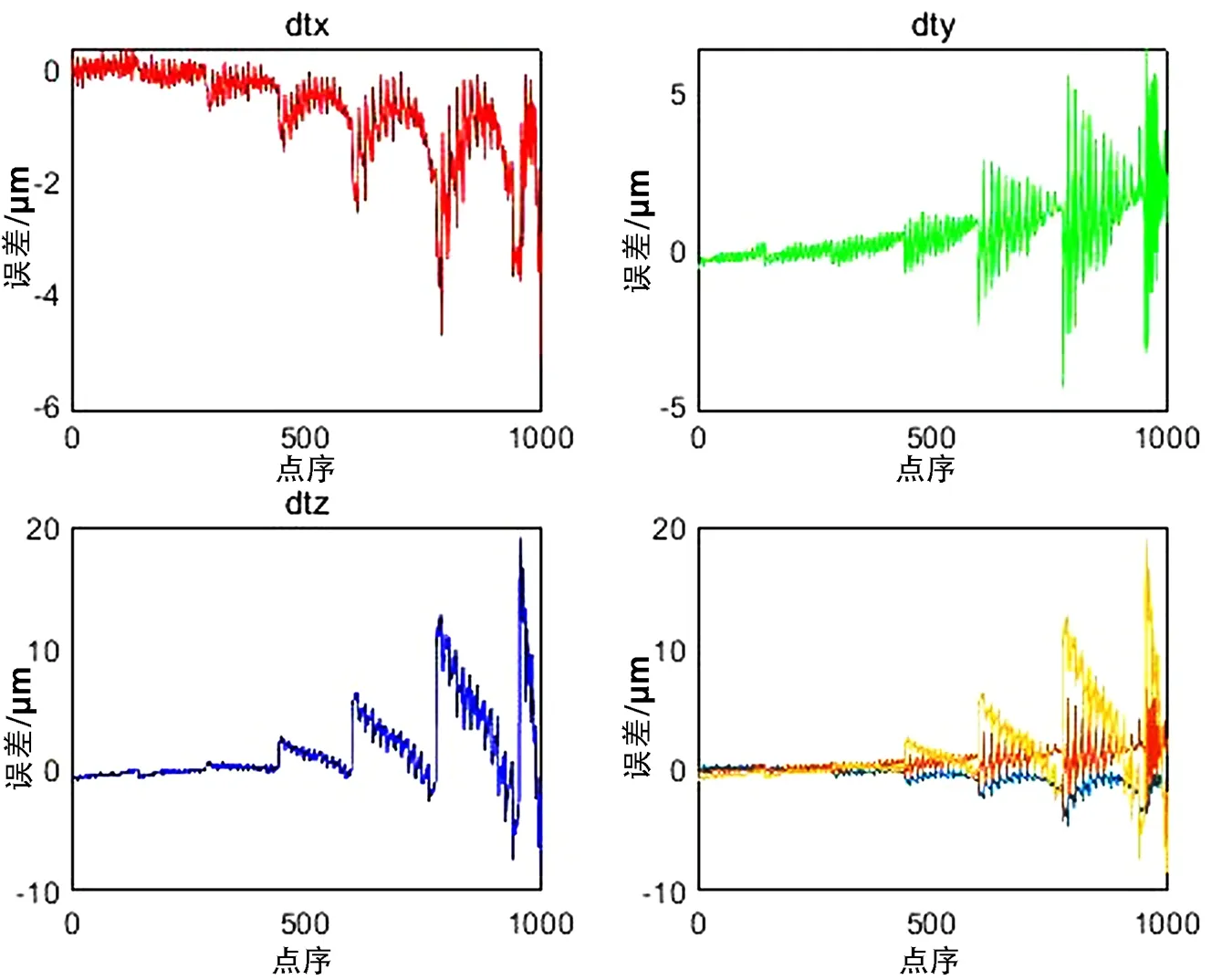
圖8 雙目平移誤差
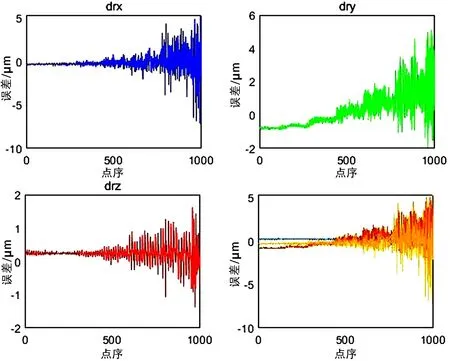
圖9 雙目角度誤差
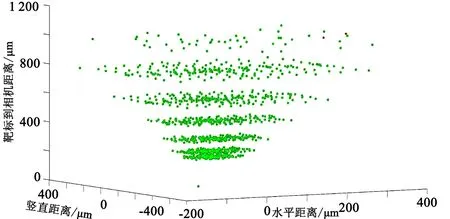
圖10 雙目測試點三維分布(綠色點不超差、紅色點超差)
5 自動化標定平臺的不確定度分析
手眼相機自動化精度測量存在不確定誤差,由于關節測量臂定位誤差23μm,工業機器人重復定位誤差15μm,在標定過程中標定板不可避免會存在1個像素的誤差。因此用不確定度μc來評估系統誤差,由下式各個不確定度分量合成,μ1表示關節測量臂誤差,μ2表示機械臂誤差:

由式(6)可算自動化平臺的不確定度誤差約為27.5μm,由此可知自動化測試平臺的精度高,試驗的重復性良好,滿足了測量精度的要求,滿足實際的使用需求。
6 結束語
本文根據機器視覺高精度應用要求,在實際應用的手眼相機中,搭建了一套自動化精度測試平臺,開發出兼顧精度和低人力成本的雙目自動化精度測量平臺,從實驗中對位姿測量精度進行驗證,對手眼相機系統進行標定試驗并驗證視覺定位的精度分析,實驗結果表明,在此平臺下手眼相機系統定位精度達到了27.5μm,且解放雙手,通過上位機之間的相互通訊減少人為操作,此平臺具有較高精度及穩定性,滿足實際航空航天的應用需求,具有很大的實際使用價值。

