三軸線運輸車連桿轉向機構動力學建模與參數辨識*
楊飛雪,康紹鵬,強紅賓,劉凱磊,吳 昊
(江蘇理工學院機械工程學院,江蘇 常州 213001)
目前,常用的多剛體系統動力學的建模方法主要有牛頓-歐拉法、拉格朗日方程法以及凱恩法[1-3]。而參數辨識主要有最小二乘法[4]、神經網絡法、遺傳算法等。牛頓-歐拉法原理明朗并且能夠較為清晰地描述三軸線連桿轉向機構,而最小二乘法能夠較為簡便地求得未知數據,所以文中采用牛頓-歐拉法對三軸線運輸車連桿轉向機構進行動力學建模[5-6],采用最小二乘法對三軸線運輸車連桿轉向機構的動力學模型進行參數辨識。
1 連桿轉向系統數學模型
1.1 數學建模原理
牛頓-歐拉法是多剛體動力學領域使用較為廣泛的建模方法,它首先需要建立慣性坐標系和機體坐標系,再分別對多剛體系統的各個桿件進行受力分析,列寫力和力矩方程,最后結合運動學方程得到完整的動力學模型。以下方程組(1)中兩個等式分別為Newton和Euler方程:
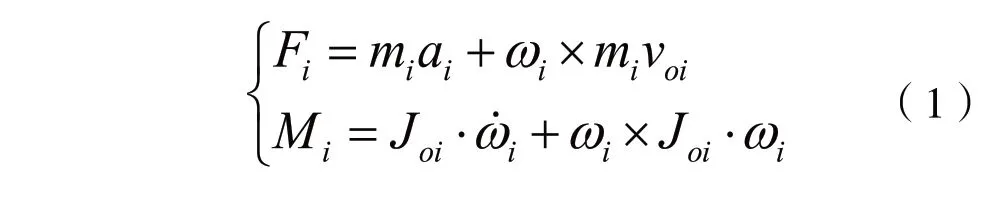
式中,Joi是第i個桿件對質心的慣量張量,ωi和分別為第i個桿件的角速度和角加速度,voi是第i個桿件的質心速度,mi是第i個桿件的質量,αi是質心加速度,Fi和Mi分別為主矢和主矩。
1.2 動力學建模
如圖1所示,三軸線連桿轉向機構中每個軸線有八個輪胎,從左到右分別為第一軸線、第二軸線和第三軸線。其中,由鉸接在車架上的液壓缸的伸縮帶動轉向臂轉動一定的角度,然后帶動鉸接在轉向臂上的兩個橫拉桿運動,而橫拉桿推動車輪上方的懸掛機構,懸掛機構帶動輪胎的轉動從而實現車輪按一定的角度進行轉向。與此同時,轉向臂的轉動還會帶動縱拉桿完成下一軸線的轉向臂的轉動,實現軸線車的整體轉向[7]。
針對圖1 建立第一軸線外側的連桿轉向[5]的動力學模型,如下所示。
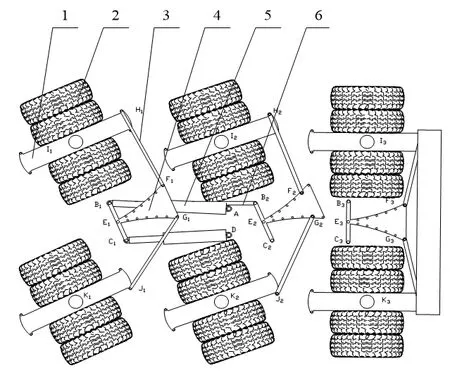
圖1 三軸線連桿轉向圖
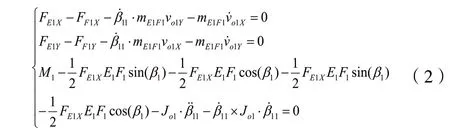
式中:FE1X是車架施加在轉向臂中心上的約束反力的x分量,FF1X是轉向橫拉桿施加在轉向臂上的約束反力的x分量,mE1F1是轉向臂的質量,FE1Y是車架施加在轉向臂中心上的約束反力的y分量,FF1Y是轉向橫拉桿施加在轉向臂上的約束反力的y分量,M1是轉向臂的主動轉向力矩,Jo1是主動杠的轉動慣量。
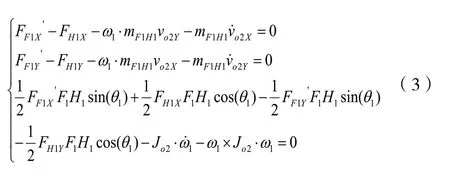
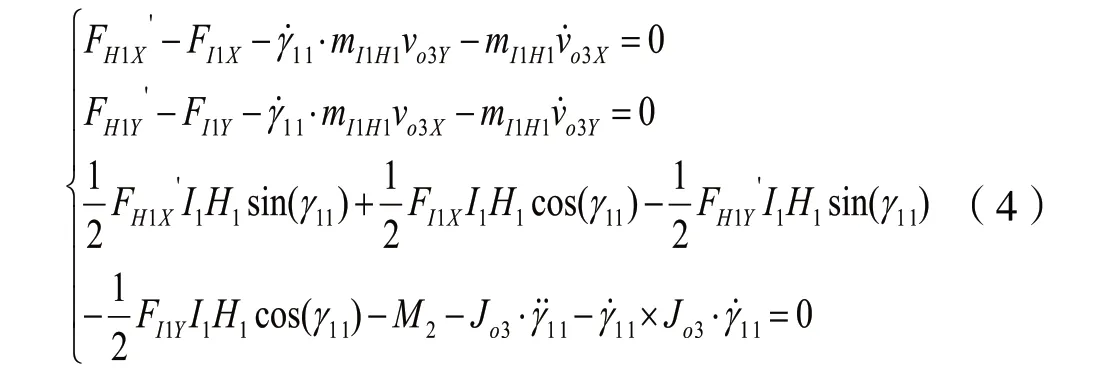
2 參數辨識
2.1 動力學方程線性化
將式(2)、(3)、(4)所建立的三軸線運輸車第一軸線外側連桿轉向機構動力學方程轉化成如下數學表達式:

其中,A1表示一個信息矩陣,x1表示待辨識參數。
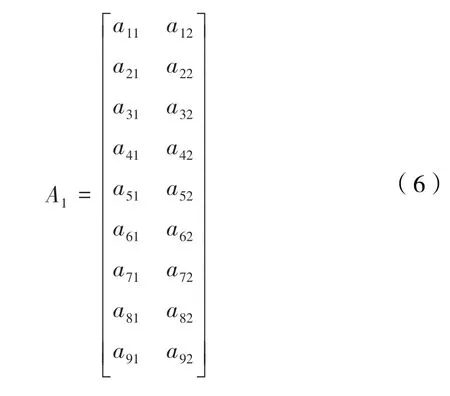
在公式(6)的矩陣中的元素如下所示:

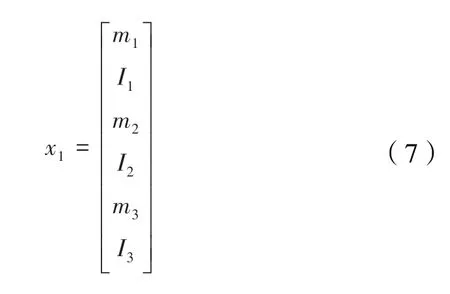
同理,第一軸線內側、第二軸線外側和第二軸線內側的數學模型可以表達為類似的數學表達式。四部分的數學表達式可以統一為公式(8)。

2.2 激勵軌跡的選擇與優化
軸線車只有在實際工作中才能進行參數辨識,也只有實際應用才有意義。因此,在進行參數辨識時,要事先設計讓軸線車充分運動的激勵軌跡,同時還要對軌跡進行優化,使激勵軌跡在滿足軸線車實際約束的同時,又能最大化地激發所有需要辨識的參數,減小誤差。因此,在軸線車的動力學參數辨識過程中,目前常用的激勵軌跡主要有多項式軌跡和周期性軌跡,多項式軌跡常用于軌跡簡單、精度要求不是很高的機器人,而周期性軌跡常用于軌跡復雜且具有循環性,同時精度要求相對較高的機器人。因此,本文選擇采用周期性軌跡規劃,將周期性軌跡設計為正弦函數和余弦函數的組合形式,通過有限次的迭加構成,也就是數學中的傅里葉級數。軸線車第i個關節的角位移的軌跡,可以用以下形式表示:
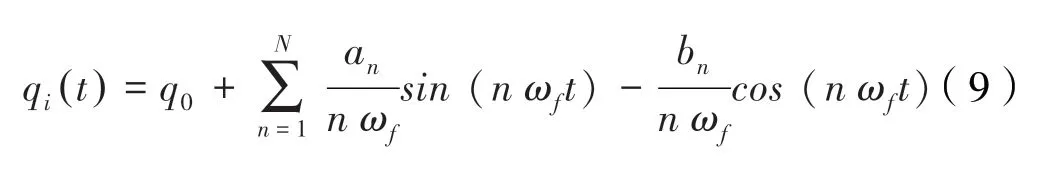
其中,ωf是傅里葉級數的基頻。傅里葉函數的周期為2π/ωf。每一個傅里葉級數包含2N+1 個參數:an和bn(n=1,…,N)是正弦和余弦函數的幅值,q0是機器人產生激勵時的關節補償。
對于一個不穩定的線性方程Ax=b,系數矩陣A和右端b都會產生一個不受控制的誤差,而矩陣A的條件數則反映了這個線性方程的性態。條件數越大,解的誤差越大,方程組被認為是病態的;條件數越小,可以認為方程組是良態的;當條件數為1 時,認為方程組的狀態最好。矩陣A的條件數定義為:
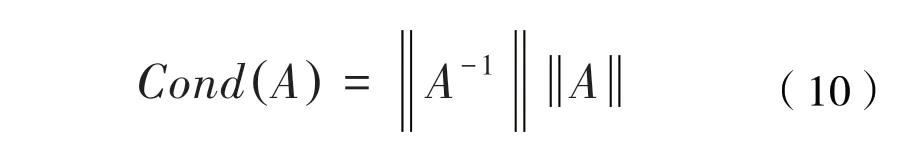
于是,確定優化激勵軌跡的問題就變為確定系數(an、bn和q0)來使觀測矩陣A的條件數最小。傅里葉函數中系數比較多,使用一般的試湊的方法計算量大并且很難得到準確值,因此必須選擇某種優化算法進行參數選擇。本文采用Matlab 中的fmincon 函數來確定激勵軌跡參數。
在三軸線運輸車連桿轉向機構中轉向臂中心會帶動其余轉向連桿進行相應的從動運動,所以只需要賦予轉向臂中心一個激勵軌跡。由式(9)可知,需要優化的參數是ai、bi(i=1,…,N)和q0,其中N=1,因此共有3個參數需要優化。
通過Matlab 中fmincon 函數并結合式(10)將激勵軌跡的求解優化問題轉化為以下的最值優化問題:
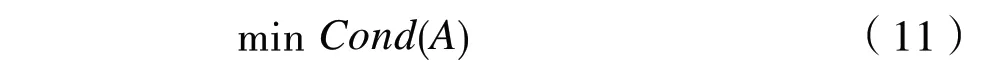
通過fmincon 函數求解出傅里葉級數參數,如表1所示。

表1 傅里葉級數最優激勵軌跡優化后參數
得到激勵軌跡如圖2所示。
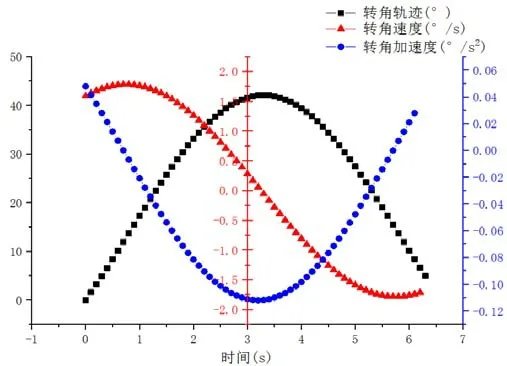
圖2 傅里葉級數激勵軌跡角度、角速度、角加速度
2.3 動力學參數辨識方法
針對動力學參數辨識,目前常用的方法主要有最小二乘法、神經網絡法、遺傳算法和極大似然估計法等。本文采用最小二乘法對已建立的動力學模型進行參數估計。
在Adams 與Simulink 的聯合仿真中,讓Adams 模型按照最優激勵軌跡運行時,實時測量相應鉸接點的轉動以及相關鉸接點的受力情況[8-9],經過計算可以得到信息矩陣A和受力矩陣b。根據式(8)可以通過最小二乘法計算參數x的值,計算方法如式(12)所示。

2.4 三軸線運輸車連桿轉向機構參數辨識
通過Adams 與Simulink 的聯合仿真將Adams 中的數據在Simulink 中通過最小二乘法進行處理可以得到三軸線連桿轉向系統中各桿件的物理參數[10]。具體參數如表2所示。
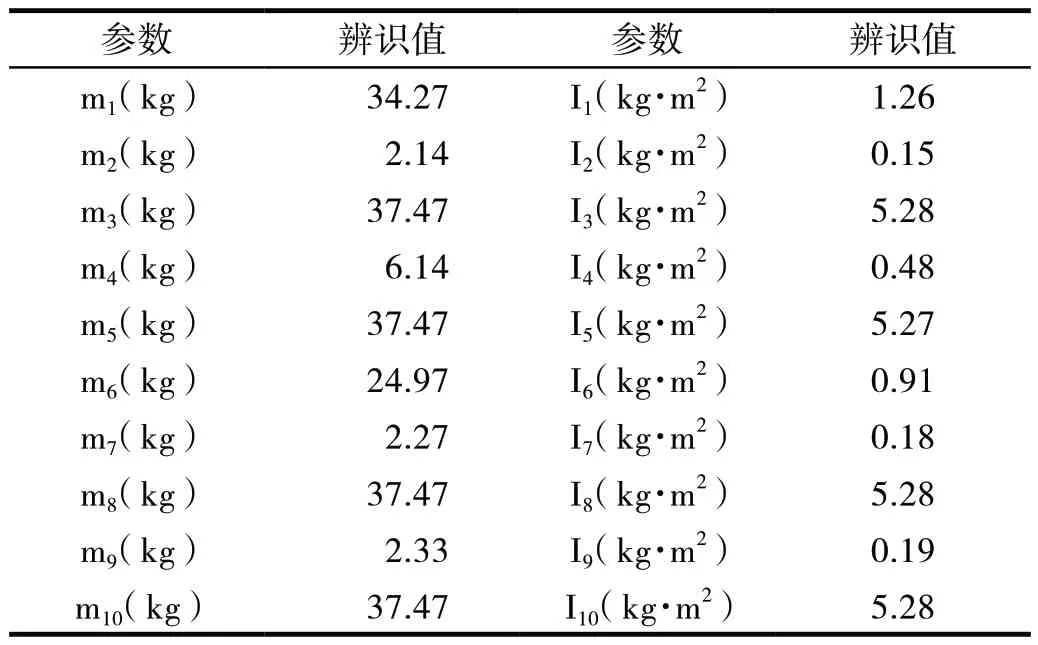
表2 三軸線運輸車連桿轉向系統動力學辨識參數
3 結語
本文通過牛頓-歐拉法對三軸線運輸車連桿轉向機構進行了動力學建模并將動力學模型進行了線性化處理。在此基礎上,選擇傅里葉級數形式的函數作為參數辨識的激勵軌跡并進行了最優化得到最優激勵軌跡。最后,采用最小二乘法并通過Adams 與Simulink 的聯合仿真,得到三軸線運輸車連桿轉向系統中各桿件的動力學參數。

