驅動耙耙齒受力分析及產品優化*

李生泉，李棟梁，楊海森，王慶凱，查開旭

（1.蘭州現代職業學院理工分院，甘肅 蘭州 730207；2.蘭州蘭石集團有限公司，甘肅 蘭州 730087）

0 引言

耙齒作為動力驅動耙的主要工具，是完成驅動耙破土、切割、攪散等操作的關鍵零件，在本次優化前的型式試驗中，目前產品出現了如圖1 所示的根部斷裂、刃部向內彎曲的嚴重質量問題，直接影響到產品的后續生產和定型[1-4]。為了短時間內找到失效原因，加快產品研發周期，本次優化在受力分析的基礎上，借助有限元手段進行了品質改善活動。

圖1 耙齒工具失效狀態

1 耙齒工具的受力分析

為了計算耙齒發生斷裂和變形時的應力，確定仿真分析時耙齒承受的最大負載，需要計算耙齒工作時的最大阻力。驅動耙作業時每個耙齒上受到的最大阻力可以認為是耙齒發生碰撞、“卡死”時的最大反作用力，本次優化過程對最大阻力的確定采用了“扭矩分配法”計算、“功率分配法”驗證的思路。

1.1 “扭矩分配法”計算阻力

確定拖拉機輸出軸輸出扭矩為T0，考慮到機器實際使用時各種情況的發生，特別是例如“大馬拉小車”的違規作業現象，根據有關標準及研究[5-8]，動力輸出軸允許輸出最大功率P0選擇為275 kW、PTO 轉速選擇為最小檔位540 r/min，將各個參數帶入式（1）求得輸出軸輸出扭矩T0為4 863.43 N·m。

式中：T0——動力輸出軸輸出最大扭矩；P0——動力輸出軸允許輸出最大功率；n0——PTO最小轉速。

同時，考慮到扭矩損失，輸出軸實際最大扭矩按照經驗值0.92 計算，帶入式（2）求得最終動力輸出軸輸出最大扭矩為4 474 N·m。

式中：T——最終動力輸出軸輸出最大扭矩。

考慮到“大馬拉小車”的極限作業情況，作業時拖拉機懸掛的驅動耙選擇為10 組刀具的小型驅動耙，帶入式（3）求得每組刀具上分配的扭矩Ti約為447 N·m。

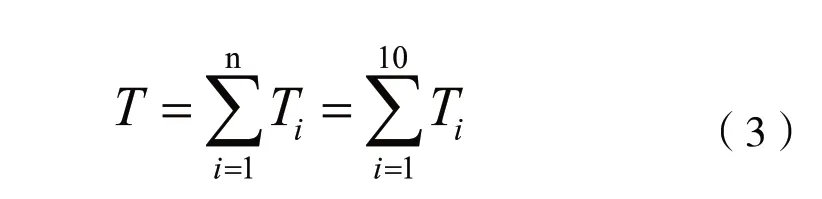
式中：Ti——每組耙齒上的最大扭矩；n——驅動耙耙齒組組數。

目前，常見驅動耙產品的耙齒間距約為24 cm～ 30 cm，優化產品每組耙齒間距0.245 m，為了計算耙齒上受到的最大沖擊力，耙齒刃部旋轉半徑R取0.12 m。根據驅動耙工作時利用每組耙齒上的力偶矩破土機理，當耙齒工作遇到暗石、樹根等堅硬物體發生碰撞、卡止現象時，由式（4）可以計算得到兩耙齒上的反作用力F0為1 990 N。

式中：F0——耙齒上的反作用力；R——耙齒間距。

當耙齒一側受到阻力無法轉動時，一組耙齒中只有一個耙齒受到阻力，此時耙齒受力演變為單齒受力模式，公式（4）演變為式（5），可求得耙齒上的最大反作用力F0為3 725 N。

1.2 “功率分配法”驗證阻力

如前文所述后傳動軸輸入功率取275 kW，考慮到拖拉機扭矩儲備因素以及驅動耙減速器和變速箱功率損失，功率損失系數η根據經驗取0.98，耙齒組數也取10，根據式（6）、（7）求得每組耙齒上的功率Pi為26.95 kW。

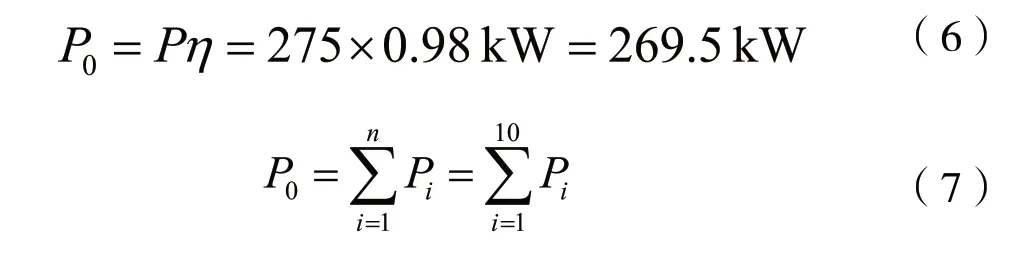
目前，常見驅動耙產品耙齒轉速一般為300 r/min～ 450 r/min，PTO 轉速與耙齒速度配置如表1 所示，R取0.12 m，耙齒轉速n取300 r/min，根據式（8）可求得每個耙齒上的破碎力F為3.58 kN。

表1 PTO轉速與耙齒速度配置

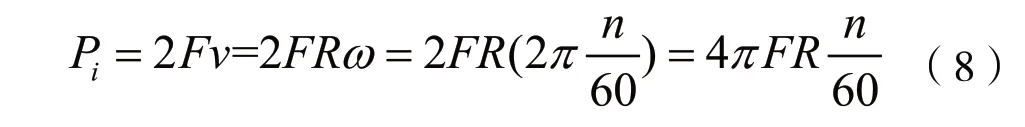
可見，用“扭矩分配法”計算的阻力與用“功率分配法”驗證的阻力相差不大，故本次優化時耙齒工作時的最大阻力取3.72 kN。

2 耙齒工作失效時受力分析

目前，耙齒失效形式主要為耙齒斷裂、內彎，仿真分析時必須研究耙齒工作時的運動狀態，以進一步確定載荷施加位置。耙齒作業時的運動軌跡如圖2 所示[9]，假設機器前進的方向為x軸方向，耕幅方向為y軸方向，耙齒上任意一點P的角速度選擇為ω、半徑為耙齒間距R，機器行進速度為vm，時間為t，根據耙齒運動軌跡可得到式（9）所示的耙齒P點（圖2 中第三象限點）的運動方程。

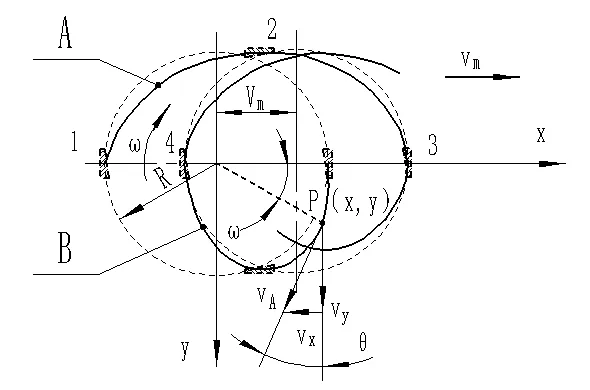
圖2 驅動耙耙齒運動軌跡圖

如前文所述，R取0.12 m、n取300 r/min，大馬力拖拉機進行耕種作業速度一般為0.8 m/s～2 m/s，vm取1.5 m/s，根據式（10）可求得vxmax為1.5 m/s，vymax為0.12 m/s。

對運動方程（9）求導，可以得到P 點的瞬時速度方程式（10）。

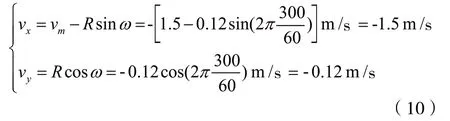
將式（10）演化為式（11），得到如圖3 所示的耙齒工作時刃部角度為85.4°（4.6°），這個角度也是耙齒安裝角度的設計來源。

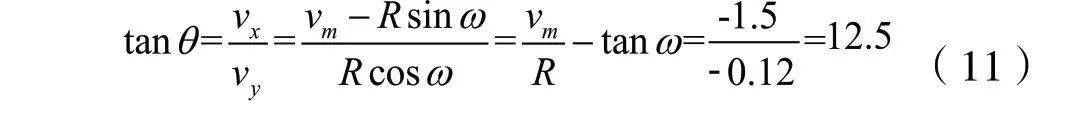
圖3 耙齒與箱體的安裝角度

根據式（11），當PTO 輸出功率達到275 kW 時，耙齒上出現最大破碎力的位置如圖4 所示，且拖拉機前進速度越大，θ 角也越大，耙齒切割土壤時產生的阻力也會明顯增大。

如圖4 所示的機具作業時，兩耙齒轉動形成的軌跡路線分別為A和B，耙齒在y軸負方向一側工作是在未破土的情況下切割土地，而在y軸正方向一側運動是在前面耙齒已破土的情況下切割土地。所以當耙齒在如圖4 所示的整周轉動中，與拖拉機前進方向一致的點2 處受到的反作用力F2要大于點4 處受到的反作用力F4、點3 處受到的反作用力F3要大于點1 處受到的反作用力F1。這就是實際工作中耙齒彎曲失效時偏向內側、耙齒斷裂失效時偏向刃口側的原因。所以在進行仿真分析時，考慮斷裂情況的載荷應該施加到如圖5 所示的刃口位置，考慮彎曲情況的載荷應該施加到如圖6 所示的側面位置，且彎曲的仿真分析中輸出值為應變值，斷裂的仿真分析中輸出值為應力值。

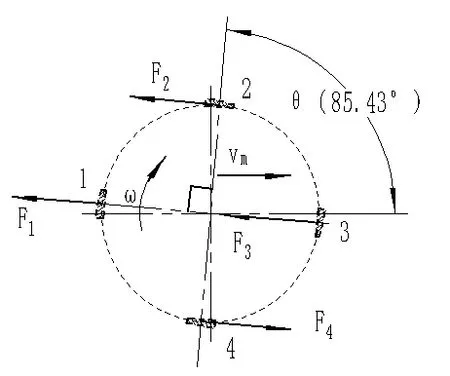
圖4 驅動耙耙齒的運動

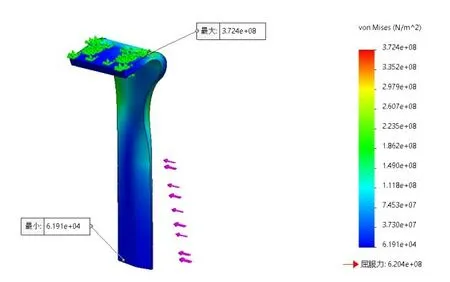
圖5 應力分析

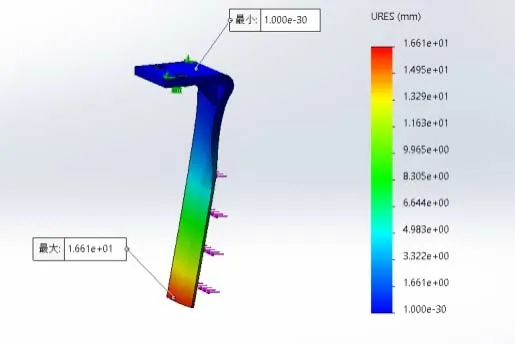
圖6 應變分析

3 試驗設計

根據已有設計經驗和產品特點，在保證耙齒硬度的基礎上[10]，本次耙齒的優化設計擬采取的優化途徑有三種：第一種是在外觀形狀上采取“直拐”式，如圖6 所示，該形狀和目前產品的形狀是當前世界上驅動耙耙齒產品的兩種代表形狀，另外為了避免耙齒向內彎曲，在耙齒彎曲位置設計了加強筋結構；第二種方法是增加耙齒厚度，考慮到后期耙齒這種易損件的加工工藝和成本，此次優化設計直接采用耙齒整體加厚的方法；第三種方法是采用某品牌產品的特殊材料。將以上三種方法編號為A、B、C，獲得如表2所示的試驗變量表。

表2 變量表

根據現代試驗方法中的交叉試驗思路，由于本次試驗只有三個因素A、B、C，為了獲得最優組合，本次試驗可直接進行全面試驗，即有8 種改進方案的仿真試驗（見表4），其中1號方案為當前產品的形狀、厚度、材料的仿真對比項。

3.1 仿真試驗階段

根據試驗設計方案，在建模軟件中完成各優化方案下耙齒模型的建立，按照圖5 和圖6 中耙齒安裝實際位置進行約束添加，之后根據前文計算和分析，在圖5 所示的刃部、圖6 所示的側面添加載荷，完成有限元網格劃分后，在刃部加載的情況下計算應力、在側面加載的情況下計算位移，經過8 次仿真計算，得到試驗結果數據。

3.2 NC函數構造

田口魯棒優化是現代優化設計中常用的方法，常用NC 函數和信噪比（SNR）函數來獲得魯棒性較好的優化方案[11-12]。

構造NC 函數時要考慮到多個優化目標的同時，將優化時間、經費以成本形式納入函數，以確保獲得最優方案，本次優化構造的NC函數為式（12）。

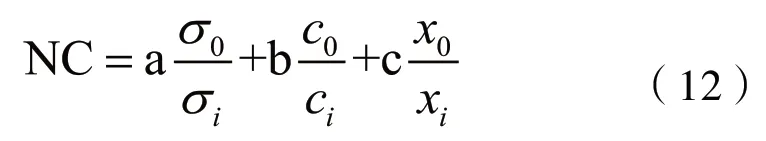
式中：a、b、c——加權因子；σ0——原應力；c0——原制造成本；x0——原位移；σi——第i種方案應力；ci——第i種方案的優化成本；xi——第i種方案的位移。

式（12）中各構造參數的取值如表3 所示，其中加權因子a、b、c 數值的選取基于對應參數對本次優化的重要程度，考慮到產品質量的保證，a、b、c 中與產品質量的相關因子取值較大。

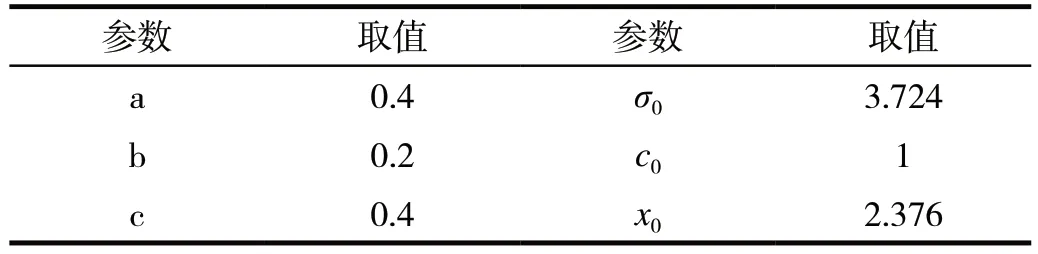
表3 系數表

3.3 信噪比（SNR）計算

試驗數據的平均值無法代替數據的穩健性，由于耙齒失效形式最終體現在應力和應變上，所以本次優化采用的是望小特性的SNR：

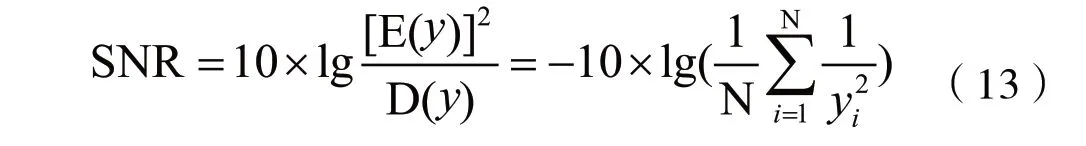
式中：yi——試驗目標值；N——試驗次數。

3.4 數據處理

根據仿真試驗結果填寫表4 中的最大應力和最大位移，計算NC和SNR后，進行其他參數的計算。

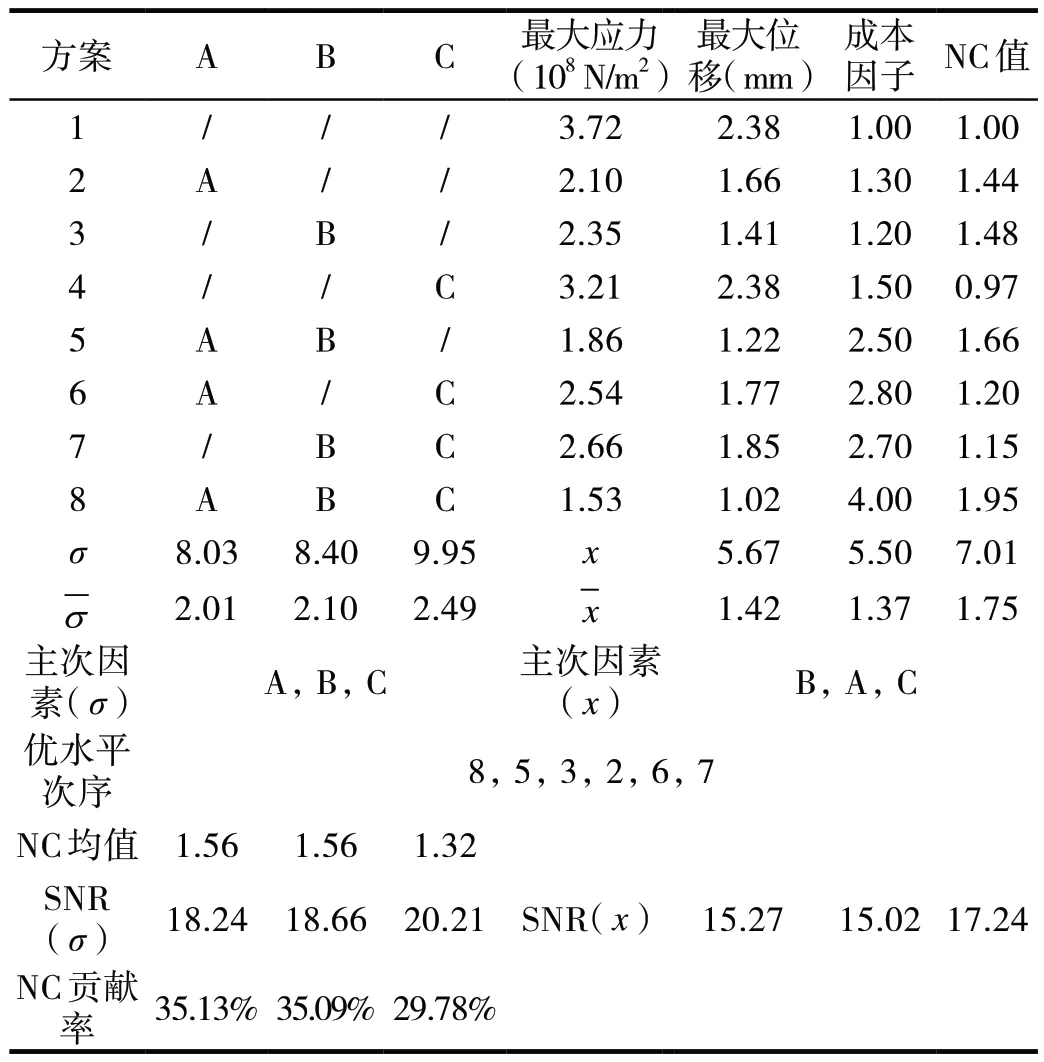
表4 試驗數據

3.5 數據分析

在表4 中，由得到的NC 值發現單變量方案4 的NC 值小于原模型下的NC 數值1，可以將這種方案淘汰；其他6 種優化方案的優水平次序為8、5、3、2、6、7。根據仿真試驗得到的應力和位移值，借助現代試驗方法中的數據處理方法，可以得出試驗中三個因素的重要順序：其中變量A 下的應力最小，位移次之；變量B 下的位移最小，應力次之；變量C 對優化目標重要程度最差，變量C 參與下的應力和位移不僅沒有明顯改善，反而增加優化成本，變量C 的魯棒性很差，這一變量應該被淘汰。雖然第8 種方案的優水平最高，但是考慮到產品試制階段現狀、銷售現狀和優化成本，第8種方案的成本過高。

為了方便比較各變量的試驗結果，完成NC 目標均值、NC 貢獻率和信噪比（SNR）坐標圖的繪制，如圖7 所示。

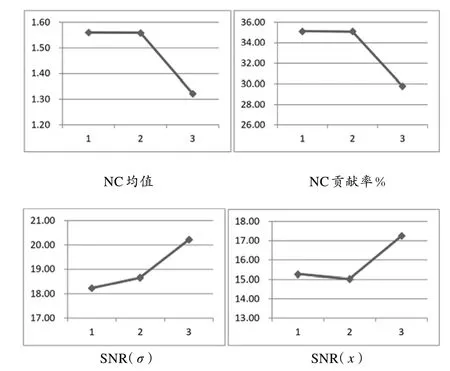
圖7 方案優化結果數據

為了進一步選取符合實際生產情況的優化方案，需要對試驗結果進行魯棒分析[13]。由NC 目標均值坐標圖可以看出耙齒形狀和厚度對此次優化的魯棒性性較好；由應力、應變信噪比坐標圖可以看出耙齒形狀和厚度的優化數據具有很好的穩定性，并且兩者的穩定性相差也不大；由NC 均值貢獻率坐標圖可以看出耙齒形狀對優化目標貢獻最大，厚度對優化目標的貢獻率稍低于耙齒形狀的貢獻，材料對優化目標的貢獻最小。所以本次優化中，形狀、厚度兩變量對優化目標的作用相當，魯棒性能、優化成本也相當，應該予以選取對應方案。

4 結論

基于以上分析，魯棒優化下的優化方案可確定為：在當前試制階段放棄材料這種周期長、不易采購的優化手段，而采用只增加厚度（2 mm）的第3 種優化方案進行試驗及推廣，后期批量生產時采用成本稍高的第5種方案。另外，考慮到耙齒受力較大的情況，將來從整機質量提升角度看，后期也可以通過在驅動耙前端加裝深松鏟機構以進一步減小耙齒受力[14]，或者將耙齒安裝形式進一步優化為具有安全銷形式的快換耙齒[15]，以進一步延長耙齒使用壽命。