基于正弦曲線和圓弧的無碳小車的S 形軌跡和凸輪設計*
吳東昊,顏景潤,康 凱,鄭永杰,任志國,劉麗娟
(河北建筑工程學院機械工程學院,河北 張家口 075000)
全國大學生工程訓練綜合能力競賽要求選擇環形運行方式的無碳小車在比賽場地中運行S 形軌跡,成功繞過障礙樁,而且運行的圈數越多,繞過的障礙樁的個數越多,比賽的成績越好。因此,無碳小車軌跡和凸輪的合理設計決定著無碳小車能夠繞過障礙樁,成功運行設定的S 形軌跡,并能夠使每一圈的軌跡有效重合,從而在比賽場地中完成多圈運行[1-3]。
1 軌跡設計
驅動車場地為5 200 mm×2 200 mm 長方形平面區域,比賽賽道分為半徑為550 mm 的半圓形賽道和長度為3 000 mm 的直線賽道,在半圓形賽道上的起點、中點和終點處放置了3 個直徑20 mm、高度200 mm 的障礙樁,在直線賽道上每間隔1 000 mm 放置了4 個同樣的障礙樁。由于無碳小車兩后輪連接線的中心點在該場地中運行的S 形軌跡是上下對稱的,所以只設計了無碳小車兩后輪連接線中心點的一半軌跡,另一半的軌跡只要按照設計好的軌跡進行對稱即可得到[4]。無碳小車兩后輪連接線中心點的一半軌跡,如圖1 所示,其中黑色粗實線表示驅動車場地的邊界,空心小圓圈表示障礙樁的位置。
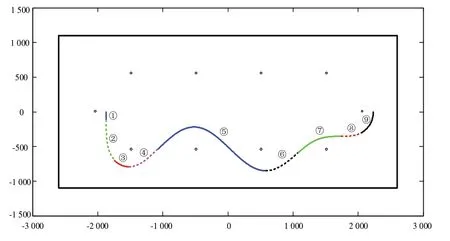
圖1 無碳小車兩后輪連接線中心點的一半軌跡
無碳小車兩后輪連接線中心點的軌跡設計采用正弦曲線和圓弧相結合的方式,從起始位置出發,第一段軌跡是直線,第二段軌跡是正弦曲線,第三段軌跡是圓弧,第四段軌跡、第五段軌跡、第六段軌跡、第七段軌跡和第八段軌跡是正弦曲線,第九段軌跡是圓弧。無碳小車兩后輪連接線中心點的軌跡采用圓弧設計,是因為圓弧的曲率是不變的,可以在兩段正弦曲線之間起到一個過渡作用,使得凸輪的形狀更加平滑[5-6]。
正弦曲線的表達式為y=A*sin(pi*x/B),式中A為振幅,B為半周期。首先確定正弦曲線的半周期B,然后通過前后兩段曲線在連接點處的斜率或曲率相等求得振幅A,最后通過上下左右平移曲線使得其和上一段曲線相接。當前后兩段曲線的曲率都等于0 時,通過旋轉使得前后兩段曲線在連接點處的斜率相等。
以第五段正弦曲線為例,根據該曲線經過的點確定半周期為1 100,然后根據前后兩段曲線的斜率相等,即A*pi/B=tan(sita4),求得A=315.13,最后將曲線向左平移x3(end)、向下平移y3(end),使其和第四段曲線相接,得到第五段曲線的函數為y=315.13*sin(pi*(x-x3(end))/1 100)+y3(end)。
對于圓弧曲線,需要求得圓弧的半徑和圓心。圓弧的半徑通過上一段曲線終點處的曲率可以得到,圓弧的圓心通過解方程組可以得到,圓弧的圓心和上一段曲線的終點過一條直線,該直線的斜率為上一段曲線終點處斜率的負倒數,可以得到兩個方程,上一段曲線的終點也是圓弧上的點,可以得到一個方程,從而通過解方程組可以求得圓弧的圓心[7-8]。
由于無碳小車兩后輪連接線的中心點在該驅動車場地中運行的S 形軌跡是上下對稱的,所以無碳小車兩后輪連接線中心點的軌跡在起點和終點處的斜率要垂直于比賽場地的水平中心線[9-10]。在起點處,軌跡是一條豎直的直線,在終點處,軌跡是一段圓弧,該段圓弧在終點處要垂直于比賽場地的水平中心線,再根據求圓弧圓心的過程,可以得到式(1)、式(2)和式(3):
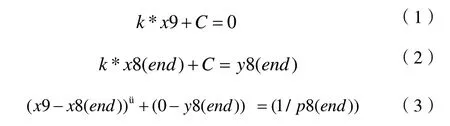
其中,x9 為該段圓弧圓心的橫坐標;k為過圓心和上一段曲線終點的直線斜率,k=tan(arctan(A1*pi/B)-sita7);x8(end)和y8(end)分別為上一段曲線終點的橫坐標和縱坐標;p8(end)為上一段曲線終點處的曲率,p8(end)=A1*pi2/B2。
根據式(1)、式(2)和式(3)可以得到式(4):
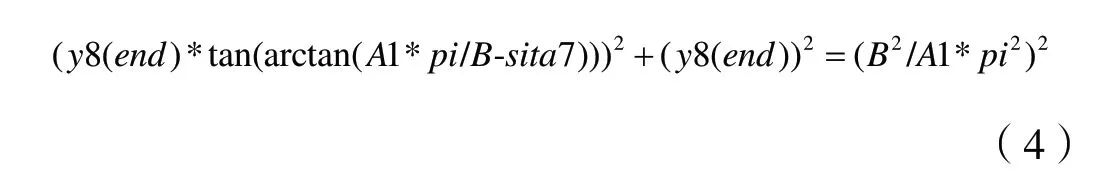
然后采用迭代法求第八段正弦曲線的參數,迭代法的過程如圖2所示。
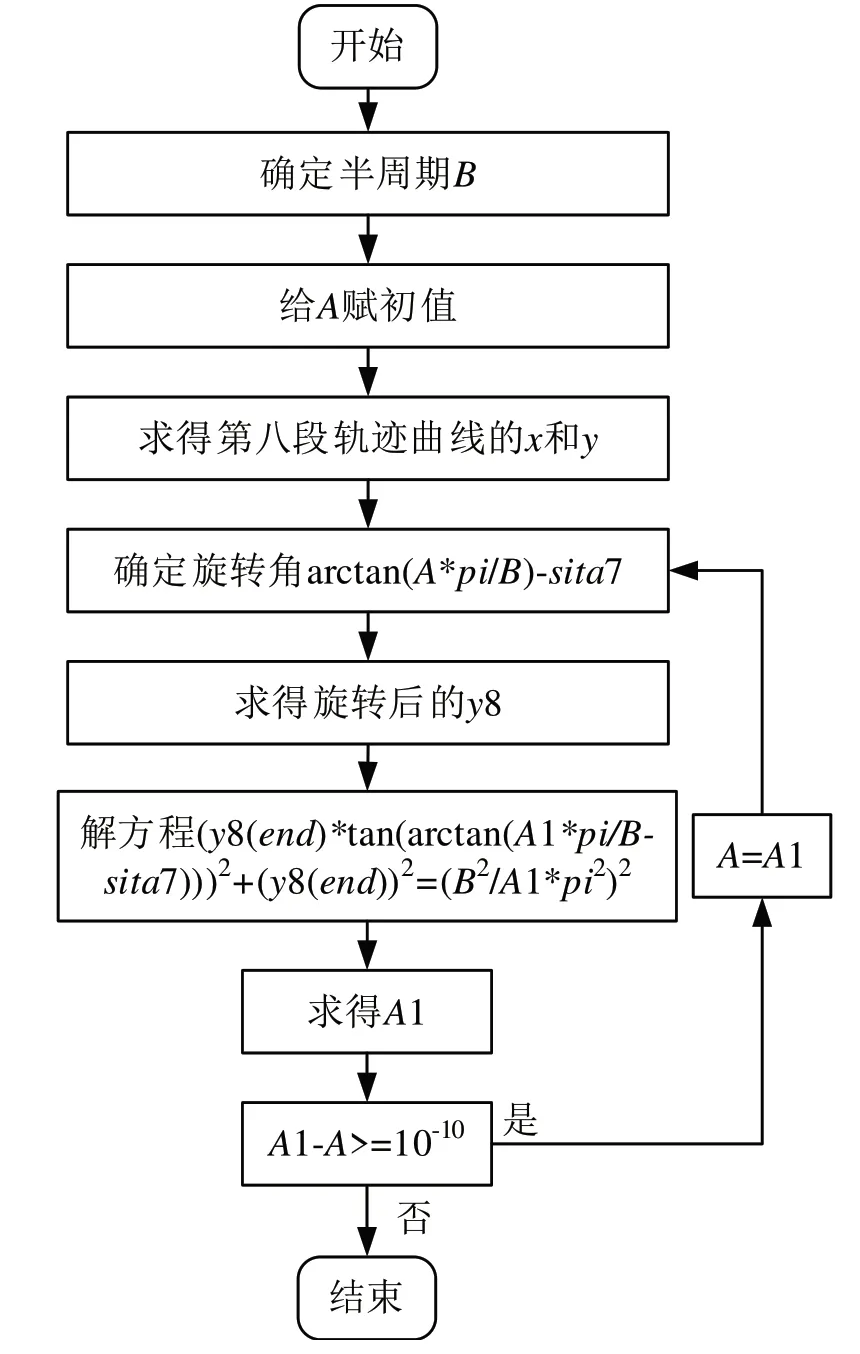
圖2 迭代法的過程
對于無碳小車前輪和兩個后輪的軌跡,根據式(5)、式(6)和式(7)可以得到前輪和兩個后輪的一半軌跡。
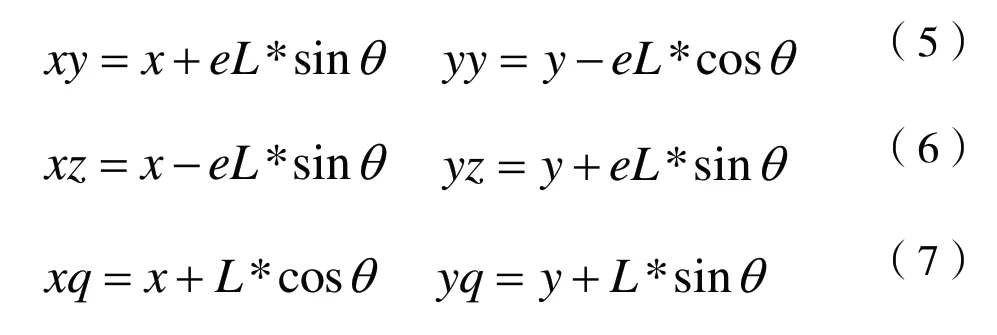
其中,x、y表示兩后輪連接線中心點軌跡的橫坐標和縱坐標,xy、yy表示右后輪軌跡的橫坐標和縱坐標,xz、yz表示左后輪軌跡的橫坐標和縱坐標,xq、yq表示前輪的橫坐標和縱坐標,eL表示兩后輪到其連接線中心點的距離,L表示前輪到兩后輪連接線中心點的距離,θ表示兩后輪連接線中心點軌跡的切線和橫坐標軸的夾角。
對于無碳小車前輪和兩個后輪的另一半軌跡,由于兩個后輪的軌跡是關于比賽場地的水平中心線對稱的,將得到的兩個后輪的一半軌跡進行對稱即可得到兩個后輪的另一半軌跡;但是由于無碳小車前輪的軌跡不是關于比賽場地的水平中心線對稱的,所以需要通過無碳小車兩后輪連接線中心點的另一半軌跡得到前輪的另一半軌跡。無碳小車前輪、兩個后輪和兩后輪連接線中心點的軌跡,如圖3 所示,其中實線表示前輪軌跡,單點劃線表示右后輪軌跡,雙點劃線表示左后輪軌跡,虛線表示兩后輪連接線中心點軌跡。
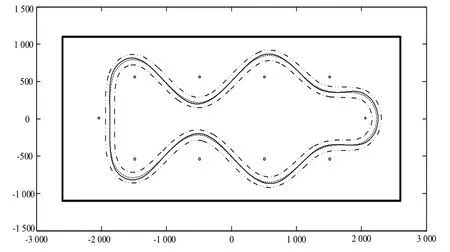
圖3 前輪、兩個后輪和兩后輪連接線中心點的軌跡
2 凸輪設計
完成無碳小車兩后輪連接線中心點的軌跡設計后,首先通過軌跡函數可以求得軌跡的曲率,再根據式(8)求得前輪轉角。
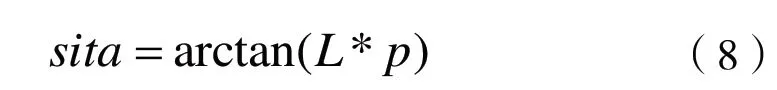
然后利用前輪轉角結合凸輪基圓半徑求得凸輪的推程,如果無碳小車左轉,根據式(9)求得凸輪推程;如果無碳小車右轉,根據式(10)求得凸輪推程。
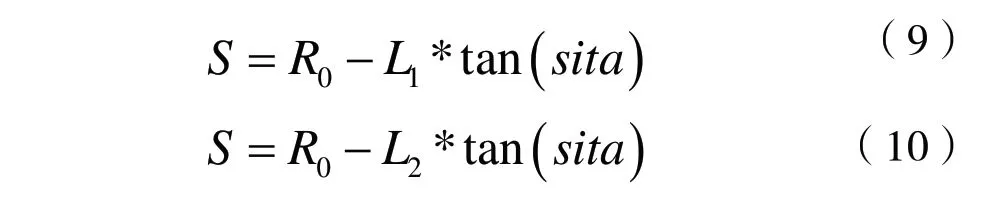
其中,S為凸輪推程;R0為凸輪基圓半徑;考慮到凸輪厚度,L1和L2分別為前輪到凸輪右邊和左邊的距離。
最后根據無碳小車兩后輪連接線中心點的軌跡求出兩后輪連接線中心點每一步運動的距離,利用式(11)求出主動輪每一步運動的距離,主動輪每一步運動的距離占主動輪運動總距離的比例與2*pi的乘積即為該推程所對應的凸輪轉角。
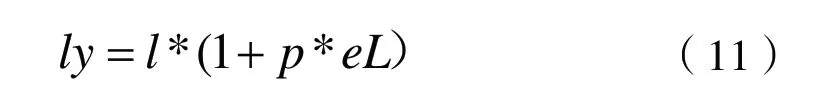
根據凸輪轉角和凸輪推程得到的凸輪形狀,如圖4所示。
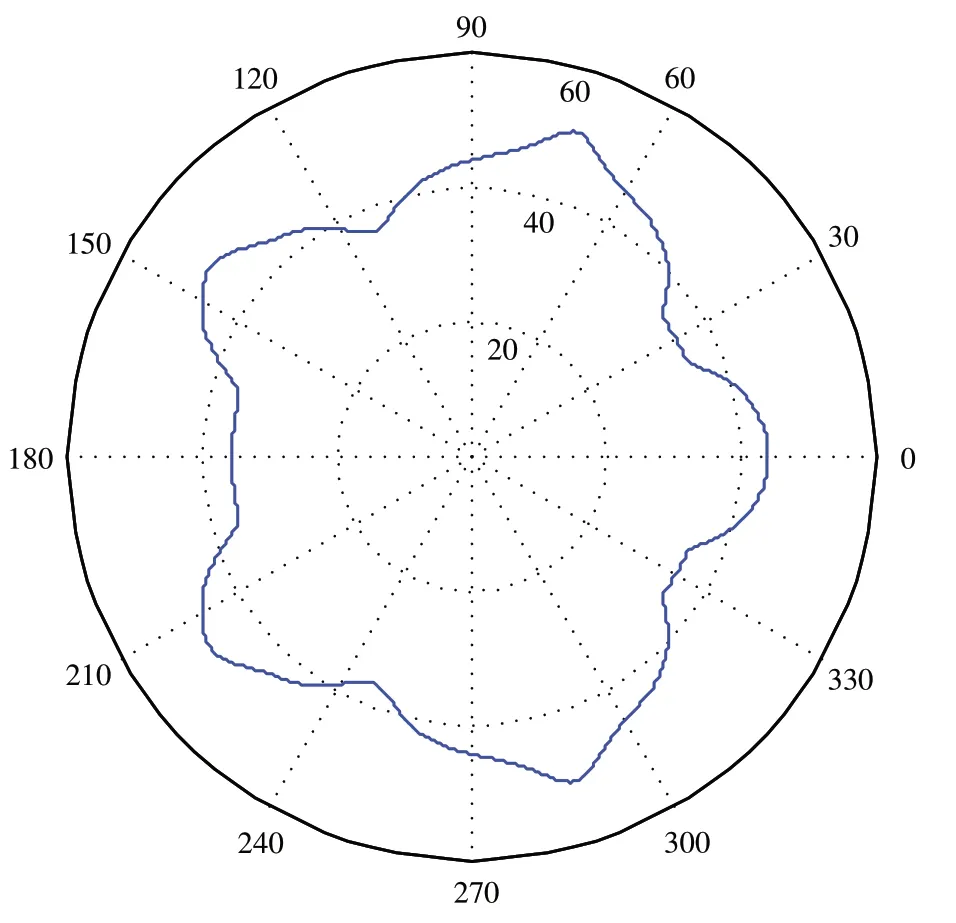
圖4 凸輪形狀
3 結論
首先采用正弦曲線和圓弧進行無碳小車兩后輪連接線中心點軌跡的設計,圓弧在兩段正弦曲線之間的過渡作用,使得凸輪的形狀更加平滑;然后利用Matlab 進行編程,驗證了軌跡和凸輪設計的合理性;最后經過實驗驗證,無碳小車能夠有效地繞過障礙樁,完成S形軌跡,滿足競賽的要求。

