基于P-NAEKF 算法的汽車行駛狀態估計

戴凌宇，馮張棋，馬成宇，胡子添

(1.南通大學 電氣工程學院，江蘇 南通 216000;2.江蘇大學 汽車與交通工程學院，江蘇 鎮江 212013;3.江蘇大學 汽車工程研究院，江蘇 鎮江 212013)

0 引言

近年來，自動駕駛技術飛速發展，其安全性被社會廣泛關注。隨著自動駕駛技術離開實驗室走向社會，將面臨更加復雜的交通狀況，為了確保車輛自身的安全性，它需要準確感知面臨的環境并做出合理決策［1］。目前很多高精度的傳感器因為產品價格問題不能普及到所有的汽車，有些關鍵狀態參數難以直接量測，所以需要使用一些較為廉價的傳感器先獲取一部分狀態信息，利用這些信息對不宜直接測量的關鍵車輛狀態進行估計，有效保障汽車安全自動駕駛［2］。

目前針對汽車的狀態估計的方法主要有:擴展卡爾曼濾波、無跡卡爾曼濾波、容積卡爾曼濾波、粒子濾波、滑模觀測器和神經網絡的方法［3-8］。趙強等［9］考慮車輛側向運動、橫擺運動和側傾運動，建立非線性模型，設計了擴展Kalman濾波器來過濾噪聲追蹤實際值;方賢生等［10］將模糊控制引入到無跡卡爾曼濾波算法中，提出了一種模糊自適應無跡卡爾曼濾波算法完成車輛狀態參數估計;邢德鑫等［11］針對車輛狀態估計中的強非線性、噪聲非高斯問題設計了一種自適應容積粒子濾波狀態估計器。以Kalman 濾波理論為基礎的車輛狀態估計方法是當前研究的主流方向［12］。

郝亮等［13］基于3 自由度的車輛模型采用標準的擴展卡爾曼濾波(EKF)方法對橫擺角速度和質心側偏角進行了估計，仿真驗證了其有效性，但其噪聲特性是通過試驗和經驗得到的，難以驗證其準確性，影響了濾波效果;Li 等［14］提出了基于多種傳感器信息融合的EKF 汽車狀態估計方法，雖然考慮了多種噪聲特性集合，但本質上還是假設噪聲統計特性已知，適用范圍有限;李靜等［15］提出了一種自適應容積卡爾曼濾波，它是將標準的容積卡爾曼濾波(cubature kalman filter，CKF)與Sage-Husa 次優估計算法結合在一起，對部分車輛參數實時在線估計，雖然該方法解決了噪聲協方差的估計問題，但是Sage-Husa 次優估計方法容易使噪聲協方差失去正定性而導致濾波發散。

根據上述討論，以往對于EKF 在車輛狀態估計的研究中，在噪聲協方差的不準確性問題上還存在一些不足，為了改善這一問題，本文分析了噪聲協方差不準確給狀態估計結果帶來的影響，給出了2 種噪聲協方差的估計方法:基于Sage-Husa的次優估計方法和基于粒子群的噪聲協方差優化估計方法，分析了Sage-Husa 次優估計算法容易發散和過于依賴統計特性的不足，選擇粒子群算法對不精準的噪聲協方差進行優化估計，并將這一部分作為參數估計模塊與傳統EKF 算法相結合，提出噪聲自適應的EKF 算法(P-NAEKF)，該算法能在噪聲協方差不準確時對其進行估計修正，大大提高了濾波精度，經過仿真驗證，這種算法能夠完成車輛行駛狀態的準確估計。

1 3 自由度車輛模型

1.1 模型構建

構建基于縱向車速，橫擺角速度和質心側偏角的3 自由度模型［13］如圖1 所示。

圖1 3 自由度非線性模型示意圖

圖1 中，XOY 是以車輛質心為原點的坐標系，其中:X 軸與車輛的縱向對稱軸重疊，并且選擇向右為正方向;Y 軸通過車輛的質心，并選擇向上為正向。選擇質心側偏角，橫擺角速度和縱向速度為狀態量，選擇縱向加速度為量測量，選擇橫向加速度和方向盤轉角為控制量構建如下的3 自由度非線性汽車狀態方程:

式中:β 為車輛質心側偏角;ω 為車輛橫擺角速度;u 為車輛縱向速度;ax為車輛縱向加速度;ay為車輛側向加速度;δ 是車輛的前輪轉角。

1.2 模型轉換

使用擴展Kalman 濾波算法對式(1)進行狀態估計，假設u 在采樣周期T=0.01 s 內不變，將汽車狀態方程離散化:

將式(1)與式(3)聯立方程組并移項可得

式中，相關參數值如表1 所示。

表1 車輛參數

2 傳統EKF 算法及問題描述

2.1 傳統EKF 算法

基于式(3)和式(4)可知狀態方程和量測方程可以表示為:

式中，狀態變量x=［β，ω，u］T，輸出變量z=［ay］T，控制變量u=［δ，ax］，wk-1與vk為互不相關的高斯白噪聲，且服從正態分布。

傳統的EKF 用于汽車狀態估計時，噪聲協方差R 和過程噪聲協方差Q 往往是通過不斷調試或是經驗得到的［16］，此時可以得到EKF 的迭代方程:

式中:A 和H 是通過求取狀態x 的雅可比矩陣得到的，將式(4)和式(5)展開可得式(13)和式(14)，再依據式(15)和式(16)求解得到A 和H。

2.2 性能匹配分析

在實際汽車狀態估計時，復雜的路況環境是千變萬化的，傳感器受到干擾往往會導致噪聲協方差存在誤差，對濾波性能的干擾是極其巨大的［16］。當系統存在不匹配的噪聲方差，可以得到:

式中:Rk表示真實的量測噪聲協方差;Qk|k-1表示真實的過程噪聲協方差;上標f 表示實際應用假設值;ΔRk和ΔQk|k-1表示實際應用假設值和真實值的偏差。

在濾波過程中，通常用估計誤差協方差來表示濾波估計的均方誤差(mean squared error，MSE)，根據不準確的噪聲方差和乘性噪聲相關系數，得到不準確的均方誤差(FMSE)為:

其中

式中，上標f 表示濾波器實際的計算值，但是這個計算值與真實值存在一定的偏差，所以并不是真實的MSE。真實的均方誤差(TMSE)為:

其中

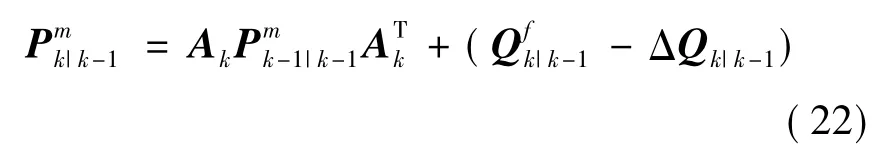
對比式(19)和式(21)可以發現，當噪聲協方差存在誤差時，仍然使用不精準的噪聲協方差來設計Kalman 濾波器，將會導致估計誤差協方差與真實的TMSE 存在偏差，Kalman 濾波器的精度降低，因此有必要設計一種噪聲自適應濾波算法解決噪聲協方差不精準的問題。

3 2 種參數優化估計方法

3.1 基于Sage-Husa 的噪聲協方差估計方法

Sage-Husa 算法［17］是一種利用協方差特性估計噪聲協方差的方法，該方法已得到證明，現作簡要描述:

式中，dk=(1-c)/(1-ck+1)，0＜c＜1 為遺忘因子。

但是直接使用這種算法估計噪聲協方差存在一些問題:

1)式(23)和式(24)中運用了減法運算，雖然能夠滿足無偏估計的要求，但容易使得噪聲協方差失去正定性導致濾波發散。

2)過于依賴噪聲統計特性，估計效果取決于信息的好壞。

3.2 基于粒子群算法的噪聲協方差估計方法

3.1 節中介紹了基于Sage-Husa 的噪聲協方差估計方法，但存在一些問題，于是本小節以汽車狀態估計擴展Kalman 濾波器為研究對象，針對過程噪聲協方差和量測噪聲協方差不精準的情況，提出一種新的估計方法即粒子群算法估計噪聲協方差。

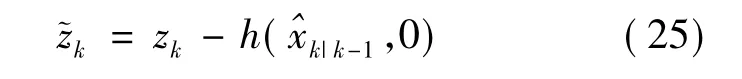
新息協方差的計算值為:

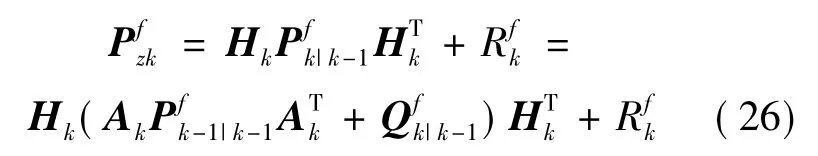
新息協方差的實際值為:

根據式(23)式(24)可以得到:

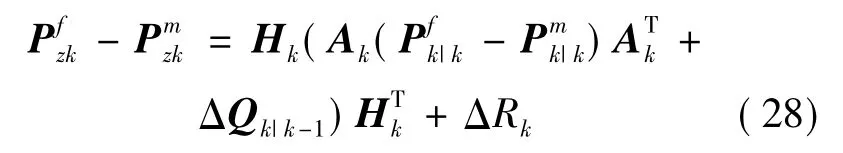
為了保證ΔRk和ΔQk|k-1盡可能小，設置適應度函數:

在每次迭代后，產生一組最優值，即個體最優值(gbest)和全局最優值(pbest)，粒子通過最優值更新位置和速度，即:

通過迭代尋優得到適應度最小的粒子位置b=(b1，b2，…，bD)T，即得到噪聲協方差的估計值:

該算法與3.1 節提出的傳統Sage-Husa 方法相比，保證了正定，提高了算法的收斂性。

參數估計算法流程圖2 所示。

圖2 噪聲協方差估計算法流程圖

4 P-NAEKF 算法

基于3.2 節的參數估計方法，可以得到較為準確的噪聲協方差的值，將這種參數估計方法嵌入傳統的EKF 算法中，可以得到P-NAEKF 算法。

P-NAEKF 算法流程如表2 所示。

表2 P-NAEKF 算法流程

5 仿真分析

5.1 Carsim 與Matlab/Simulink 聯合仿真平臺

在本文中，首先在Carsim 中搭建車輛模型，并設定工況［18］，將其與Matlab/Simulink 中建立的傳統的EKF 算法模塊與本文的P-NAEKF 算法模塊聯合仿真，對汽車的縱向車速、橫擺角速度和質心側偏角等相關參數進行實時估計，并對比估計結果，驗證P-NAEKF 算法的優越性。

聯合仿真平臺如圖3 所示。

圖3 Carsim 與Matlab/Simulink 聯合仿真平臺框圖

工況設定:選取Carsim 中自帶的雙移線工況，路面附著系數為0.855，其他車輛參數見表1 所示，準確的噪聲參數為:

將傳感器測量的縱向加速度、側向加速度以及方向盤轉角信號作為估計模塊輸入信號，3 個輸入信號如圖4—6 所示。

圖4 側向加速度輸入信號

圖6 方向盤轉角輸入信號

5.2 參數估計

本章節使用2 種參數估計方法對噪聲協方差進行估計，進行50 次蒙特卡洛實驗，并對估計效果進行比較，結果如圖7 所示。

方法1:傳統的Sage-Husa 算法，對應文中3.1節提出的方法;

方法2:基于粒子群算法的參數優化估計方法，對應文中3.2 節提出的方法。

這一部分對過程噪聲協方差進行了估計，比較2 種不同的估計方法，觀察圖7 可以清晰地發現，方法2 的估計效果明顯好于方法1，且50 次的結果均穩定在真實值附近，誤差在0～±2.5 之間，仿真表明方法2 能夠較好地估計過程噪聲協方差。

圖7 過程噪聲協方差估計結果

這一部分對量測噪聲協方差進行了估計，使用了方法1 和方法2 并做了比較，從圖8 可以清晰地發現，方法2 的估計效果明顯好于方法1，且50次的估計結果穩定在真實值附近，誤差在0～0.02之間，仿真表明方法2 能夠較好地估計量測噪聲協方差。

圖8 量測噪聲協方差估計結果

綜上所述，本文提出的參數優化估計方法可以在噪聲協方差不準確情況上估計出準確的噪聲協方差，為車輛狀態估計提供保障。

5.3 汽車狀態估計

為了便于描述，現對狀態估計算法做如下簡化定義:

算法1:傳統的EKF 算法即2.1 節介紹的算法，其中噪聲協方差使用不準確的固定值:

算法2:本文提出的P-NAEKF 算法，對應第4章提出的算法，其中已知不精準的噪聲協方差與算法1 設置一樣，實際算法采用的噪聲協方差通過5.1 節的方法2 估計得到。

通過傳統EKF 算法估計的縱向車速以及本文提出的P-NAEKF 算法估計的縱向車速與Carsim輸出參數值進行對比分析。縱向車速的狀態估計仿真結果如圖9 和圖10 所示。

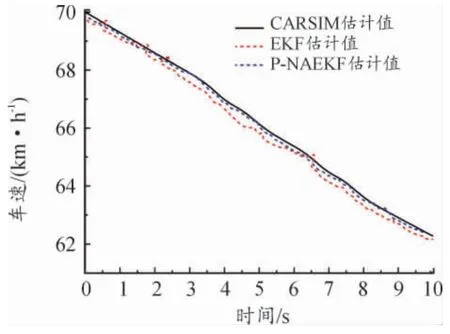
圖9 縱向車速曲線

圖10 縱向車速濾波偏差曲線

從圖9 和圖10 可以發現，P-NAEKF 算法的估計效果明顯優于EKF，最大誤差僅為0.2 m/s，數值波動能夠處于穩定狀態，且與實際數值接近;而EKF 的最大誤差達到了0.5 m/s。

通過傳統EKF 算法估計的橫擺角速度以及本文提出的P-NAEKF 算法估計的橫擺角速度與Carsim 輸出參數值進行對比分析。橫擺角速度的狀態估計仿真結果如圖11 和圖12 所示。

從圖11 和圖12 可以發現，P-NAEKF 算法的估計效果明顯優于EKF，其估計值一直處于真實值附近，誤差很小，而傳統的EKF 在某些時刻存在發散現象。

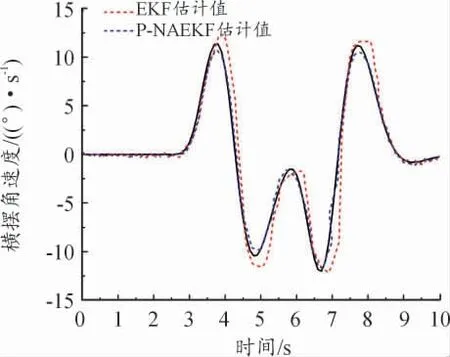
圖11 橫擺角速度曲線

圖12 橫擺角速度濾波偏差曲線

通過傳統EKF 算法估計的質心側偏角以及本文提出的P-NAEKF 算法估計的質心側偏角與Carsim 輸出參數值進行對比分析。質心側偏角狀態估計仿真如圖13 和圖14 所示。

從圖13 和圖14 可以發現，P-NAEKF 的估計效果大大優于EKF，傳統EKF 在10 s 的時間里存在不止一次的發散現象，而P-NAEKF 算法保持較好的收斂性，其估計值位于真實值附近，最大誤差僅為0.2°左右，數值波動能夠處于穩定狀態。

圖13 質心側偏角曲線

圖14 質心側偏角濾波偏差曲線

根據仿真實驗，可以得到:在噪聲協方差獲取數值不精準的情況下，P-NAEKF 可以通過基于粒子群的參數優化估計方法對噪聲協方差進行矯正，因此P-NAEKF 具有優異的估計精度和良好的收斂性，能夠較好地解決噪聲協方差獲取不準確的情況下的車輛行駛狀態估計問題。

6 結論

1)構建了基于縱向車速，橫擺角速度和質心側偏角的3 自由度模型，考慮了縱向車速和傳統汽車狀態參數之間的非線性關系，更嚴謹地解決汽車狀態估計問題。

2)提出了基于粒子群算法的參數優化估計方法，并通過Matlab 仿真與傳統的Sage-Husa 算法進行對比，驗證了本文提出的參數估計方法的優越性。

3)提出了基于NAEKF 算法的汽車行駛狀態估計方法，通過聯合仿真驗證了該算法在噪聲協方差不準確的環境下可以提供更加準確的車輛狀態估計。