例析古典概型的交匯問題
■鄭 瑋
古典概型是一種概率模型,是概率論中最直觀和最簡單的模型。在這個模型下,隨機試驗的所有可能結果是有限的,并且每個基本結果發生的可能性是相同的。下面例析古典概型的交匯問題。
一、與集合有關的概率問題
例1 已知集合A={2,3,4,5,6,7},B={2,3,6,9},在集合A∪B中任取一個元素,則它是集合A∩B中的元素的概率為( )。
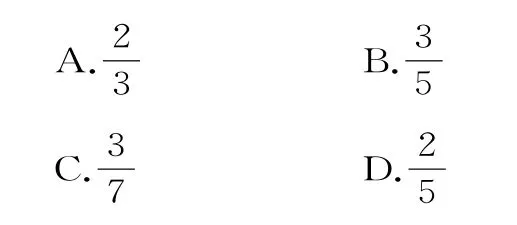

評注:古典概型的兩個基本特征,即有限性和等可能性。在應用古典概型的概率公式時,關鍵是正確理解隨機事件和樣本點的關系,事件和樣本空間的關系。
二、與函數有關的概率問題
例2 已知a∈{-2,0,1,2,3},b∈{3,5},則函數f(x)=(a2-2)ex+b為減函數的概率是( )。

評注:涉及函數的概率問題,解題的關鍵是求出所求事件包含的樣本點的個數。
三、與向量有關的概率問題
例3 設連續擲兩次骰子得到的點數分別為m,n,令平面向量a=(m,n),b=(1,-3)。

四、與幾何圖形有關的概率問題

評注:求與幾何圖形有關的概率問題,應充分利用幾何圖形的性質。
五、與游戲有關的概率問題
例5 某兒童樂園在“六一”兒童節推出了一項趣味活動。參加活動的兒童需轉動如圖1所示的轉盤兩次,每次轉動后,待轉盤停止轉動時,記錄指針所指區域中的數。記兩次記錄的數分別為x,y。獎勵規則如下:①若xy≤3,則獎勵玩具一個;②若xy≥8,則獎勵水杯一個;③其余情況獎勵飲料一瓶。
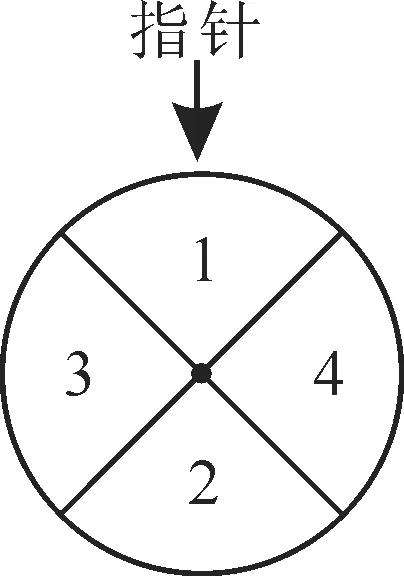
圖1
假設轉盤質地均勻,四個區域劃分均勻。小亮準備參加此項活動。
(1)求小亮獲得玩具的概率。
(2)請比較小亮獲得水杯與獲得飲料的概率的大小,并說明理由。
解:用數對(x,y)表示小亮參加活動先后記錄的數,則樣本空間Ω與點集S={(x,y)|x∈N*,y∈N*,1≤x≤4,1≤y≤4}一一對應。因為S中元素的個數是4×4=16,所以樣本點的總數n=16。

評注:生活中的概率游戲問題,背景真實,內容鮮活,具有知識性、娛樂性、趣味性和益智性。
六、與取球有關的概率問題
例6 一個盒子里裝有標號1,2,3,4的4個形狀大小完全相同的小球,先后隨機地選取2個小球,根據下列條件,分別求2個小球上的數字為相鄰整數的概率。
(1)小球的選取是無放回。
(2)小球的選取是有放回。
解:記事件A=“選取的2個小球上的數字為相鄰整數”。


評注:對于不放回抽樣,計算樣本點個數時,既可以看成是有順序的,也可以看成是無順序的,其最后結果是一致的。但不論選擇哪一種方式,觀察的角度必須一致,否則會產生錯誤。對于有放回抽樣,在連續取出兩次的過程中,因為先后順序不同,所以(a1,b),(b,a1)不是同一個樣本點。解答本題的關鍵是要分清“無放回抽取”與“有放回抽取”,且每一件產品被取出的機會都是均等的。

