飛機(jī)降落過程數(shù)學(xué)模型研究

黃河基，陳世杰，馬珺凌，郭嘉俊，周以明（中國民航大學(xué)理學(xué)院，天津 300300）

飛機(jī)最危險(xiǎn)的十一分鐘：起飛三分鐘，降落八分鐘，這是因?yàn)樵谄痫w、降落過程中大多處于對流層，此處的氣流變化較為顯著，且高度有限，飛行員不能夠很好地對飛機(jī)做出修正，一旦沒有控制好力度，很容易造成飛行事故。本文通過建立飛機(jī)降落過程的物理模型、數(shù)學(xué)模型，得到兩段飛機(jī)降落時(shí)的二次曲線，并利用Matlab對各個(gè)階段的數(shù)據(jù)進(jìn)行了擬合分析，從而分析各個(gè)階段飛機(jī)的受力情況，得到所需要提供的力的大小，最后針對數(shù)值計(jì)算結(jié)果對模型進(jìn)行修正、改進(jìn)。

一、飛機(jī)降落過程的力學(xué)模型

飛機(jī)在降落過程中一共收到四個(gè)力的作用（如圖1所示），分別為：升力、阻力、飛行員提供的推力和飛機(jī)的重力（飛機(jī)在空中的阻力一共包括摩擦阻力、壓差阻力、干擾阻力、激波阻力和誘導(dǎo)阻力。但其中摩擦阻力、壓差阻力、干擾阻力和激波阻力都與升力無關(guān)，即為廢阻力，因此此處只考慮誘導(dǎo)阻力的影響）。

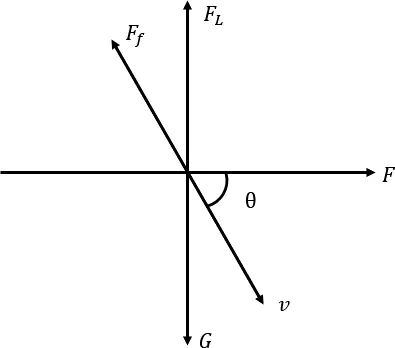
圖1 飛機(jī)降落時(shí)的受力情況

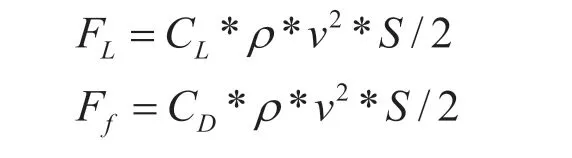
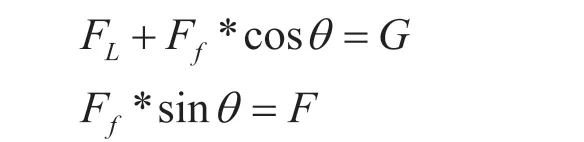
（其中FL為升力、Ff為阻力、F為飛行員提供的推力、G為飛機(jī)的重力、θ為阻力與水平方向的夾角、v為飛機(jī)的飛行速度、S為飛機(jī)的機(jī)翼面積、CL為飛機(jī)的升力系數(shù)、CD為飛機(jī)的阻力系數(shù)。）

二、飛機(jī)降落過程的數(shù)學(xué)模型

本文模型搭建是在一個(gè)二維平面中搭建的，也就是模擬飛機(jī)不受橫向作用影響的理想下降過程。

根據(jù)飛機(jī)在降落過程的速度恒定不變，并且在降落的初始和末尾豎直方向上的速度均為0，因此可以考慮將它分解成兩個(gè)二次曲線來進(jìn)行建模[1]。

因此本文建立的數(shù)學(xué)模型將飛機(jī)的整個(gè)降落過程分為兩個(gè)部分且均為二次曲線（如圖2）。

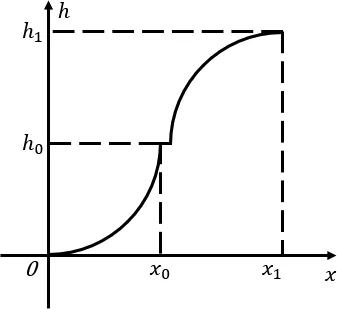
圖2 飛機(jī)降落的曲線

第一階段為從巡航高度開始降落，并且始終保持勻速，即在這個(gè)階段始終保持受力平衡，因在下降過程中影響飛機(jī)升力和阻力的一些因素的參數(shù)大小不斷變化，本文擬合變化曲線后取了最優(yōu)值以將其變?yōu)橐粋€(gè)定值以便搭建模型。

第二個(gè)階段為進(jìn)近階段，即飛機(jī)降落的最后一個(gè)階段，在這個(gè)階段之前，飛行員需要預(yù)留一小段與目的地的距離，能夠更好地將飛機(jī)飛行方向調(diào)整到落地方向以及跑道方向，但在進(jìn)行數(shù)值計(jì)算時(shí)，由于這段距離很小，所以可以忽略不計(jì)。

第一階段：

下落曲線為：

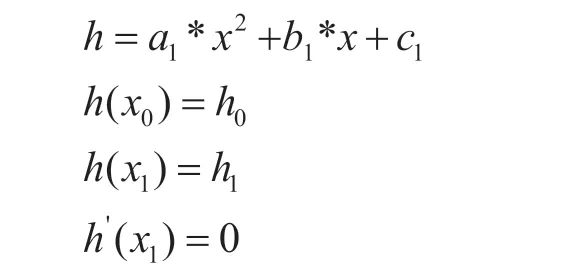
解得：

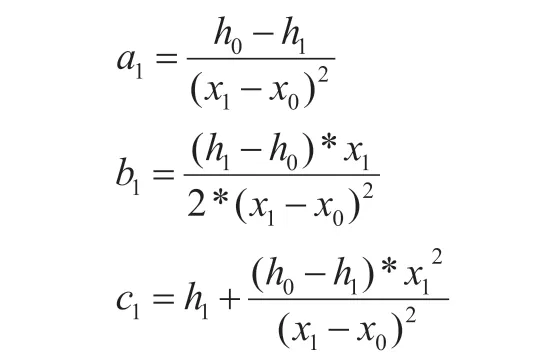
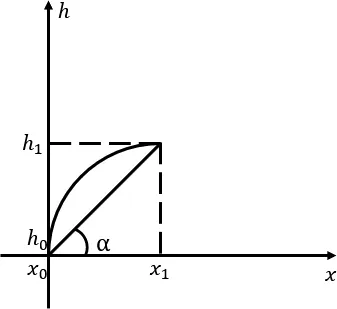
圖3 飛機(jī)降落的第一階段

第二階段：

下落曲線為：

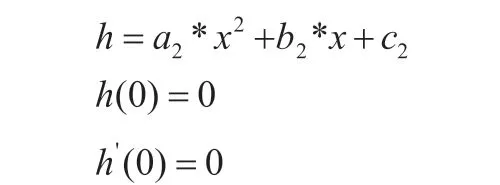
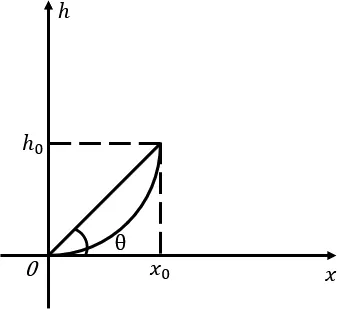
圖4 飛機(jī)降落的第二階段

解得：

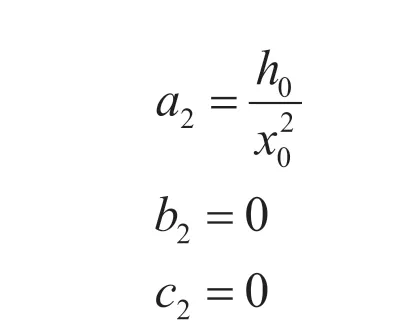
由于空氣密度會隨著海拔高度的不斷變化而變化，因此需要確定空氣密度與海拔高度之間的函數(shù)關(guān)系。

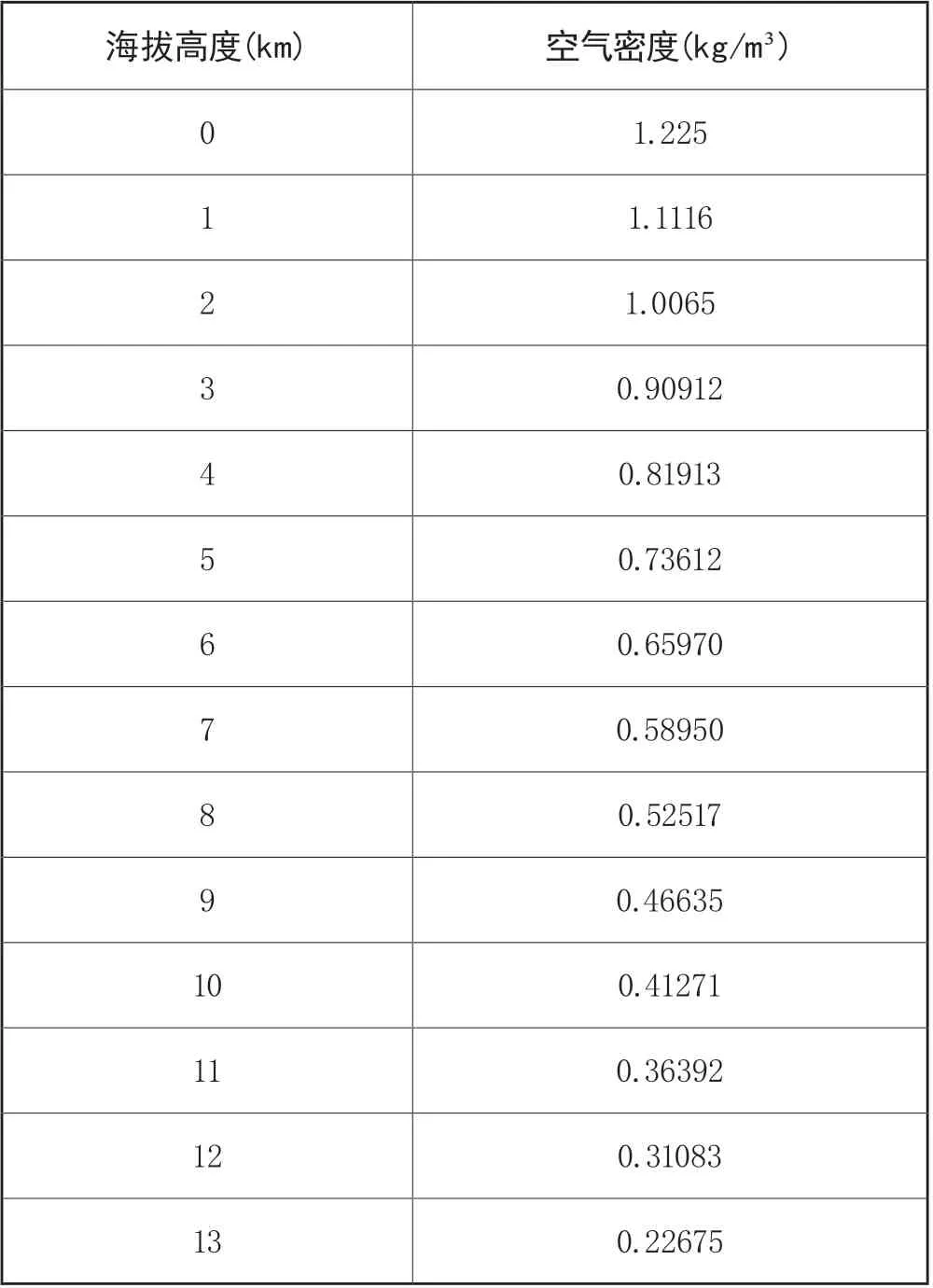
表1 空氣密度ρ與海拔高度間的關(guān)系

運(yùn)用Matlab將給定參數(shù)進(jìn)行擬合之后得到空氣密度與高度的關(guān)系式。

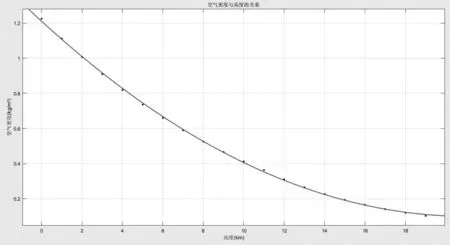
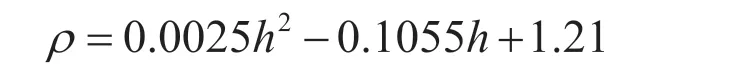
綜合以上所有數(shù)據(jù)以及建立的力學(xué)模型，通過受力平衡可以預(yù)測在不同階段的不同高度下飛行員所需要提供的水平推力大小。

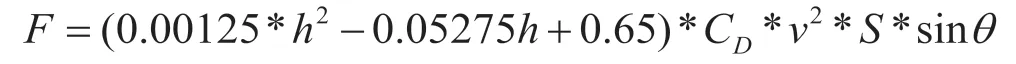
（其中θ為阻力與水平方向的夾角、v為飛機(jī)的飛行速度、S為飛機(jī)的機(jī)翼面積、CD為飛機(jī)的阻力系數(shù)、h為海拔高度。）

三、數(shù)值分析與計(jì)算

波音公司的飛機(jī)作為現(xiàn)在比較常見的民航機(jī)型，選取此公司的機(jī)型做模型數(shù)據(jù)以用于建模和計(jì)算，現(xiàn)民航對于波音737的使用較多，則此處選取波音737-700機(jī)型，所以得到機(jī)翼面積為125.1（m2），巡航速度為852.9（km/h）。

在飛機(jī)降落的過程中，飛機(jī)的降落姿態(tài)呈抬頭，重力的受力方向不與升力相同，存在一個(gè)抬頭角度，抬頭方向與其速度方向并不一致，而抬頭角度的確定由具體情況而定，本文考慮飛機(jī)始終保持平飛狀態(tài)，因此可以取飛機(jī)飛行的迎角始終為0，即得到升力系數(shù)：0.1，阻力系數(shù)：0.2。

目前客機(jī)正常巡航高度為11(km)，進(jìn)近高度為1(km)。因此設(shè)定降落第一階段的初始高度為h1=11(km)，第二階段的初始高度為h0=1(km)。

考慮到安全因素，飛機(jī)在豎直方向的加速度a≤g/10［g為重力加速度，此處取9.8（m/s2）］。

飛機(jī)在豎直方向上的速度vy是海拔高度h關(guān)于時(shí)間t的導(dǎo)數(shù)，vx是水平距離x關(guān)于時(shí)間t的導(dǎo)數(shù)，豎直方向上的加速度是豎直方向上速度vy關(guān)于時(shí)間t的導(dǎo)數(shù)，因此可以得到方程組：

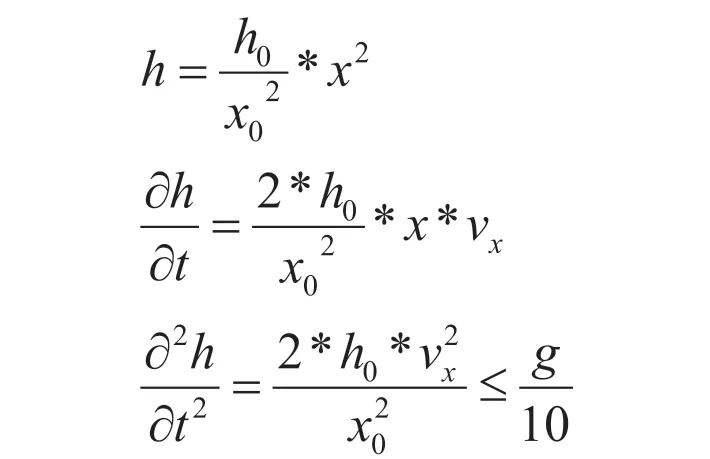
因?yàn)樾枰珳?zhǔn)且安全著陸，因此我們需要得到下降點(diǎn)距離目的地的兩個(gè)水平距離的最小值。

由上述不等式解得第二階段降落的水平安全距離：

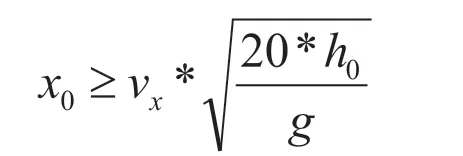
同理可得第一階段降落的水平安全距離：

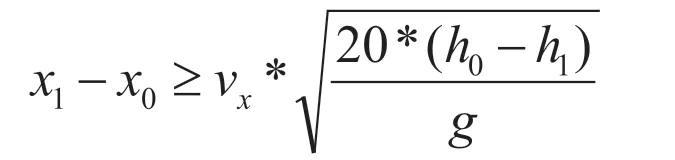
解得兩個(gè)階段下降點(diǎn)距離目的地的兩個(gè)水平距離的最小值：

設(shè)位移偏角為α，速度的偏角為θ，由于模擬的二次曲線可以理解為平拋運(yùn)動，而由平拋運(yùn)動的運(yùn)動規(guī)律則可得到：

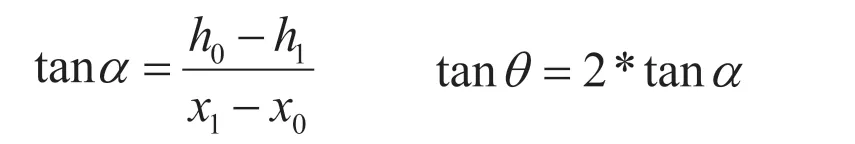
解得水平夾角θ：

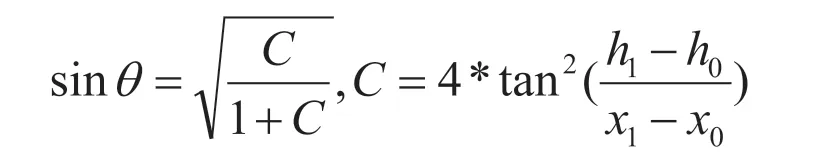
代入數(shù)據(jù)之后得到F的大小，F(xiàn)在不同高度的大小：

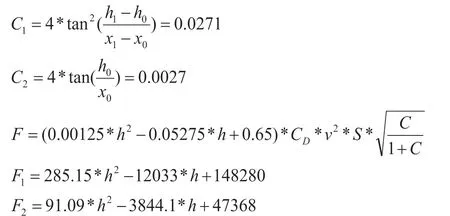
（其中F1為在第一階段的推力的大小，F(xiàn)2為在第二階段的推力大小。）

四、結(jié)束語

則在飛機(jī)飛行高度h≤1(km)時(shí)，通過這個(gè)降落模型飛機(jī)可以由公式F2來參考發(fā)動機(jī)的推力大小。在飛機(jī)飛行高度h＞1(km)時(shí)，飛機(jī)可由公式F1來參考發(fā)動機(jī)的推力大小。

經(jīng)計(jì)算：

F1（h=11)=136532.12(N)

F1（h=1)=50420.15(N)

F2（h=1)=43614.99(N)

F2（h=0)=47368(N)

則第一階段的發(fā)動機(jī)推力在50 420.15(N)至136 532.12(N)之間，第二階段的發(fā)動機(jī)推力在43 614.99(N)至47368(N)之間，模型構(gòu)建完畢。