綜掘巷道架管機三節臂的軌跡分析與優化
王小龍,洪東炳,賈志軍,2,朱鵬坤
1安徽理工大學機械工程學院 安徽淮南 232001 2安徽省智能礦山裝備與技術工程實驗室 安徽淮南 232001
隨 著礦山提、運、采、掘四大裝備自動化、智 能化水平日益提升,輔助安裝設備的機械化、自動化和智能化水平的提升就顯得尤為重要。井下架管機是一種重要的輔助安裝設備,通過核心部件機械臂來實現運管、架管、接管和固管等功能。為了提高架管效率,國內外學者對機械臂進行了大量研究,王君等人[1]通過 MATLAB Robotics Toolbox 對 UR5 機器人建立模型,再對其進行軌跡規劃與仿真的研究,驗證了機器人運動模型和 3 次多項式插值算法的正確性和合理性;李威等人[2]對三節臂挖掘裝置建立運動學模型,采用遺傳算法對優化模型求解,并對實例進行分析,驗證了此優化方法有較高的應用價值;于瑞等人[3]基于雜交算法對機器人的運動時間實現了最優軌跡規劃。以上述相關研究為基礎,結合煤礦巷道的實際工作要求,筆者采用 3-5-3 多項式插值算法對三節臂進行軌跡規劃,結合粒子群算法,實現了速度約束下三節臂軌跡規劃時間的優化。
1 綜掘架管機的結構設計
目前大部分礦區仍然采用人工架管的方式,尤其在兩淮地區,架管效率較低。煤礦巷道斷面通常選擇直墻半圓拱形,凈斷面寬度為 4.2 m,高度為 3.4 m,管道安裝高度在 1.7~2.6 m,在沒有適合的輔助安裝設備下,工人勞動強度大,急需改善。
1.1 架管機的工作原理
針對上述工況,筆者設計了一種煤礦輔助設備架管機,其結構如圖 1 所示。架管機主要由牽引機構、行走機構、架管機構、鉆孔機構、載人作業機構和運管機構等部分組成。架管機通過牽引機構到達指定工作位置,由鉆孔機構對工作區域進行打孔作業,之后架管機構夾取管道,將其提升到一定高度,再協同載人作業機構將管道固定。其中,核心部件架管機構三節臂的運動軌跡決定了架管工作的效率,因此筆者對架管機構三節臂進行了軌跡優化分析。
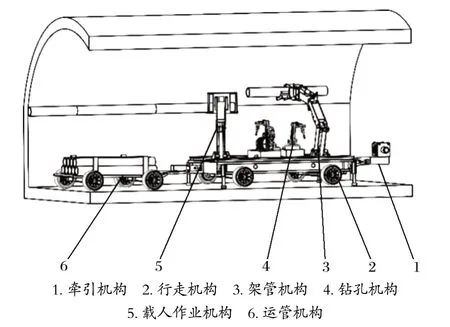
圖1 架管機結構Fig.1 Structure of pipe erector
1.2 架管機三節臂結構
架管機三節臂結構如圖 2 所示,主要由回轉裝置、第一節臂、第二節臂、第三節臂、夾管器和相應的液壓缸組成。與兩節臂結構相比,三節臂增加了架管的高度,通過輔助液壓缸可以調節夾管器的角度。
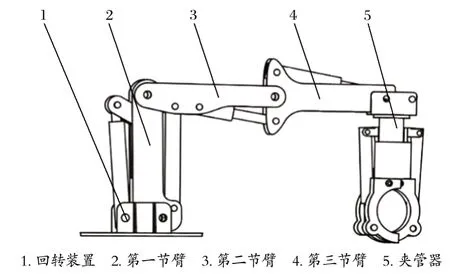
圖2 架管機三節臂結構Fig.2 Structure of three-section arm of pipe erector
2 架管機三節臂的軌跡規劃
為了清楚描述三節臂工作時的路徑狀態,判斷末端位置是否滿足巷道架管要求,筆者采用粒子群優化算法,以 3-5-3 多項式插值算法[4]對其運動過程中的關節位置、速度、加速度進行規劃,優化三節臂的工作時間。
2.1 多項式插值函數構造
3-5-3 多項式規劃是指在關節規劃中,關節在時間t1采用 3 次多項式進行規劃,在時間t2采用 5 次多項式進行規劃,在時間t3采用 3 次多項式進行規劃。在工作空間內,對三節臂進行軌跡規劃,設置其工作路徑,利用 3-5-3 次多項式對三節臂進行插值,設置 4 個插值點,用θij表示關節i插值的角度,其中i=1,2,…,n,n表示關節數,j=1,2,3,4,表示插值的 4 個序號。
第i個關節 3-5-3 樣條多項式的通式為
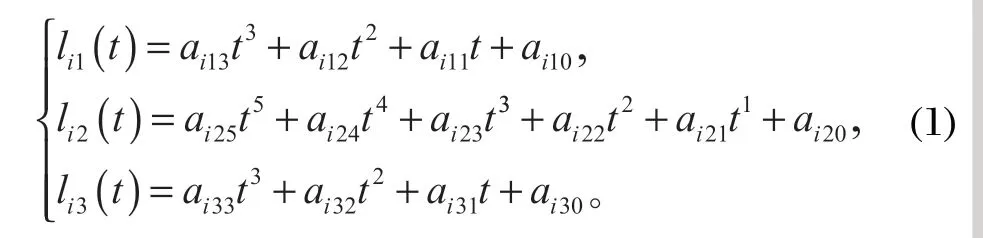
式中:li1(t)、li2(t)、li3(t) 分別代表第i段關節在 3 次多項式的運動軌跡、5 次多項式的運動軌跡、3 次多項式的運動軌跡;其中,未知系數a可根據約束條件求出,并根據約束條件和約束邊界求出矩陣A[5],用θ=[θi0,θi1,θi2,θi3] 代表第i個關節的 4 個插值點 (弧度值)。已知條件為第i個關節的初始點θi0、路徑點θi1和θi2、末端點θi3以及起止速度 0,則
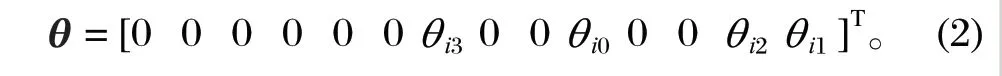
根據已知條件,推導出求解未知數a與插值點的關系式為
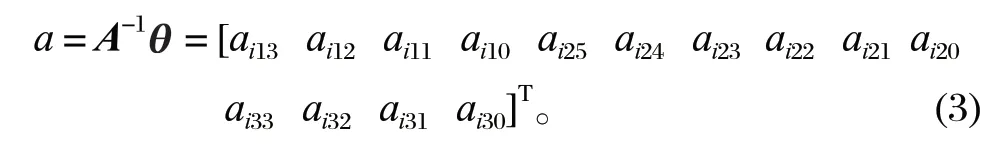
2.2 基于粒子群算法的軌跡優化
粒子群算法[6]是對軌跡時間優化的一種方法,是在鳥群捕食過程中受到的啟發,將每個個體看作 D 維空間內一個微粒,在搜索空間內以一定速度運動,通過個體之間相互協作和競爭來尋找最優解。在粒子群算法中,將每個需要優化的變數視為一個粒子,每個粒子都有一個適應值,由被優選函數所確定,并利用這種適應值的大小來確定粒子的最優值。在 D 維搜索空間內,每個粒子都有一個位置xi和一個速度vi,粒子經過的地方都會出現 2 個最優位置,即粒子所經歷最優適應值的位置pi和所有微粒群體目前所經歷的最優位置pg。當 2 個位置都不存在最優解時,第i個粒子就會通過式 (4)、(5) 繼續k+1 次迭代來更新自己的位置和速度,直到找到最優的適應值。
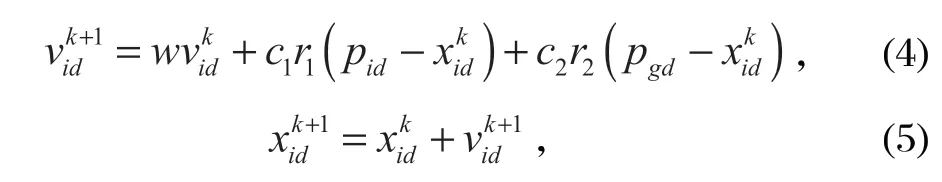
式中:vid∈[-Vmax,Vmax];w為慣性權重;c1、c2為學習因子;r1、r2為 [0,1] 之間隨機任意值;xid∈ [-xmax,xmax]。
當xid和vid符合約束條件時,就用邊界值代替,其約束條件為式中:t1、t2、t3為適應值函數。
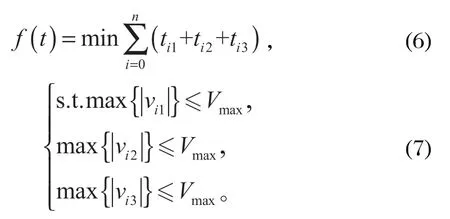
為了方便計算,將t作為自變量,搜索維度降到三維,求解位置矩陣。
粒子群算法對三節臂第i關節進行時間最優規劃的步驟為:
(1) 選取初始化種群規模,確定迭代次數,在三維空間內隨機初始化粒子的位置xi和速度vi;
(2) 給出慣性權重w和學習因子c1、c2;
(3) 計算粒子的適應值及粒子群體適應值;
(4) 調用適應度函數 fitness Trac,計算系數矩陣A,求出關節極值速度Vmax,若滿足約束條件,則說明t1、t2、t3有效,否則說明當前值無效,flag 返回 false;
(5) 根據式 (4)、(5) 優化粒子的速度vi和位置xi;
(6) 判斷粒子的速度vi和位置xi是否滿足邊界條件,若超出邊界條件,則用邊界值代替;
(7) 獲取粒子個體最優pi和粒子群體pg,判斷是否滿足結束條件,若不滿足,則回到步驟 2,反之則終止迭代。
3 仿真與分析
3.1 三節臂的運動學模型
筆者采用改進 D-H 法坐標系[7]建立架管機三節臂的運動學模型,忽略三節臂的外形和尺寸,將其結構進行簡化,得到機械臂各個關節的坐標系,如圖 3 所示。確定架管機三節臂的參數,得到 D-H 參數,如表 1 所列。
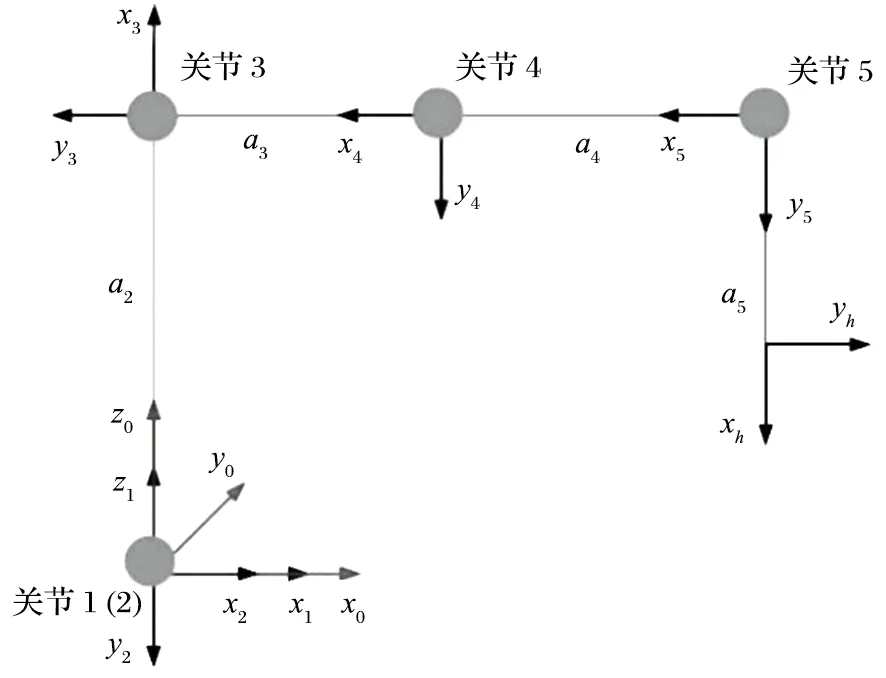
圖3 三節臂連桿坐標系簡圖Fig.3 Sketch of coordinate system of three-section arm linkage
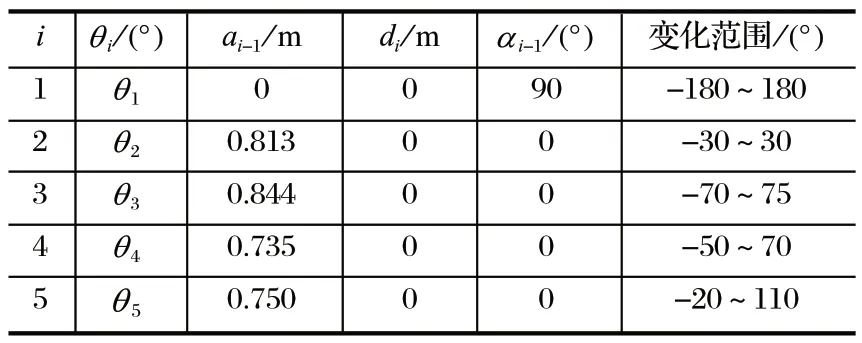
表1 架管機三節臂的 D-H 參數Tab.1 D-H parameters of three-section arm of pipe erector
以基座坐標系為基準,依次完成各個關節坐標系的轉換,坐標系 {i=1} 到 {i} 的變換矩陣ii-1T由 4 個基礎變換矩陣相乘得到,
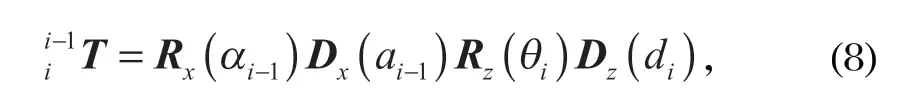
其中
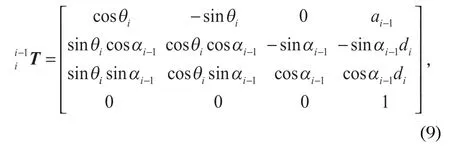
式中:ai-1表示從zi-1到zi沿xi-1測量的距離;αi-1表示從zi-1到zi沿xi-1旋轉的角度;θi表示從xi-1到xi沿zi旋轉的角度;di表示從xi-1到xi沿zi測量的距離。
由表 1 可知,每個相鄰連桿的位置變換矩陣相乘,即可得到三節臂的末端矩陣
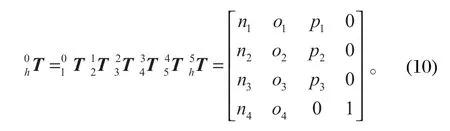
3.2 仿真結果分析
給出三節臂的 4 個位置,即起始點θi0、抓取點θi1、路徑θi2和終止點θi3,利用 3-5-3 多項式插值進行仿真,關節空間角度插值點如表 2 所列。在架管機三節臂工作時,為了架管過程中管道平穩性和安全性,關節 1 回轉盤需要處于靜止狀態,因此,關節 1 的 4 個位置始終為 0。
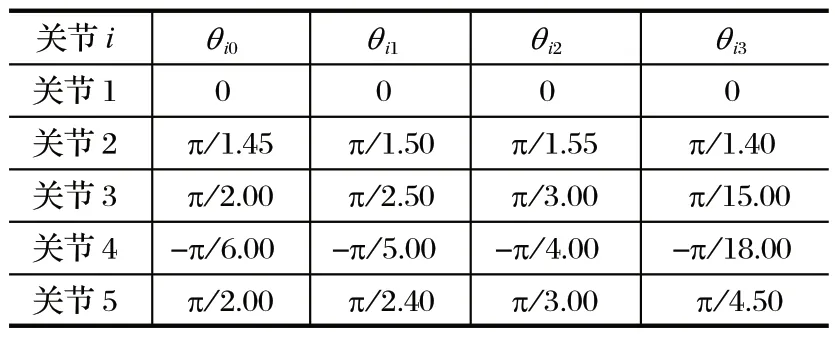
表2 關節空間角度插值點Tab.2 Interpolation points of joint space angle
根據粒子群算法最優規劃步驟,利用基于粒子群的 3-5-3 多項式插值算法,確定每段插值的最優時間。確定插值的粒子種群數為 50,迭代次數為 100,粒子的慣性權重w=0.8,學習因子c1=c2=2,允許的最大速度Vmax=3 rad/s,起止點的速度和加速度都為 0,得到關節位置進化圖,如圖 4 所示。由圖 4 可以看出,在速度約束下,4 個關節最優粒子pg位置進化曲線中,關節 2 經過 56 次迭代趨于收斂;關節 5 經過 18 次迭代后快速收斂;其余收斂均在 20~40 次之間。所以關節 5 相對平穩,說明在架管過程中末端夾管器處于穩定運動狀態。
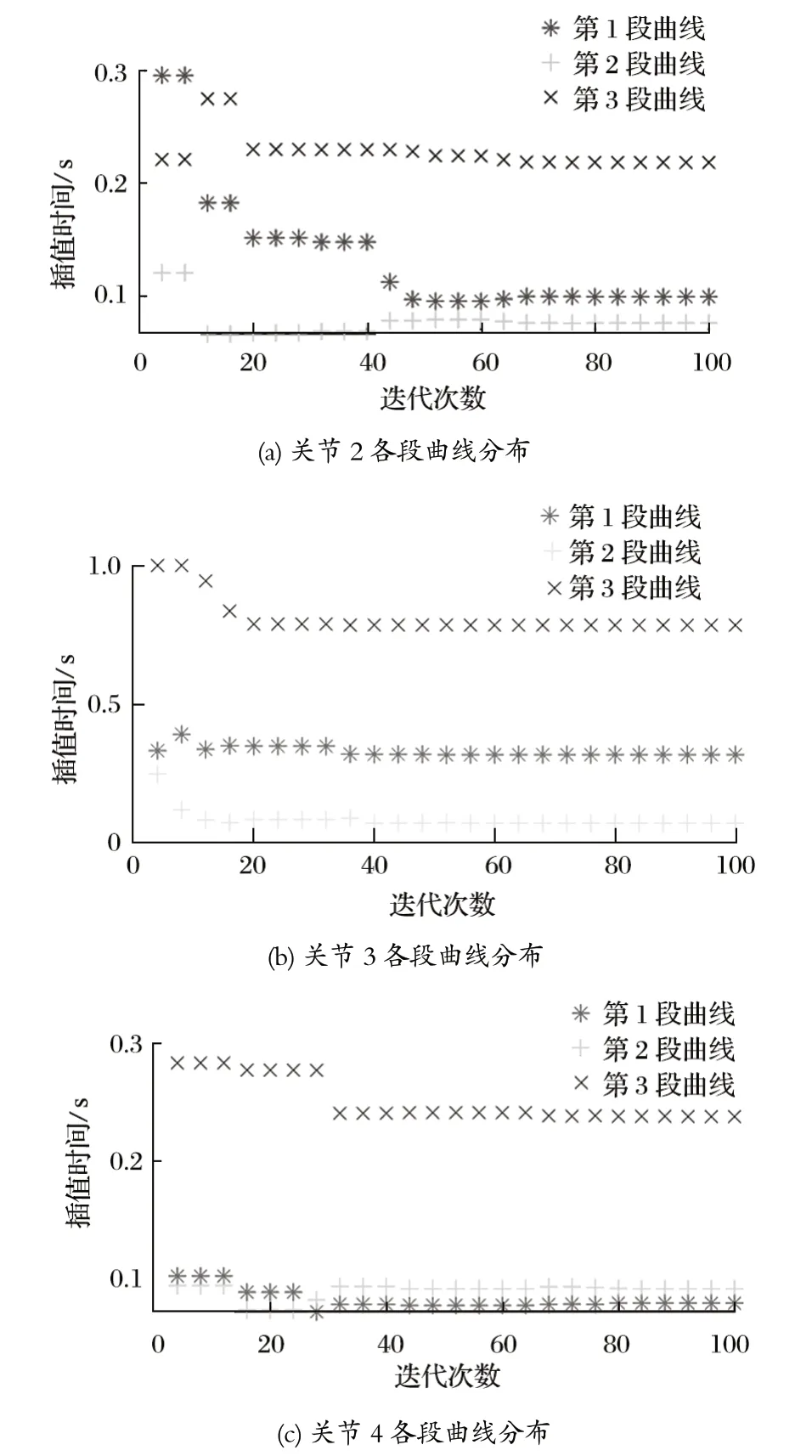
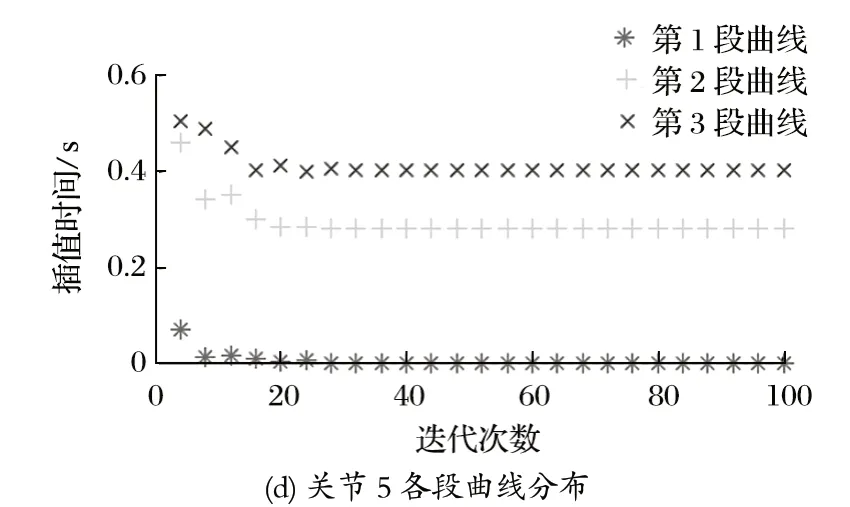
圖4 關節位置進化圖Fig.4 Evolution of joint position
3-5-3 多項式插值仿真軌跡曲線如圖 5 所示。在給定各段時間具體插值準則的情況下。初始和終點的速度和加速度都為 0,滿足運動學約束要求,其中t1=1,t2=1,t3=1;三節臂關節位置在每個時間段運動時間跨度大,速度未接近最大值,加速度在 2 s 左右出現跳變。
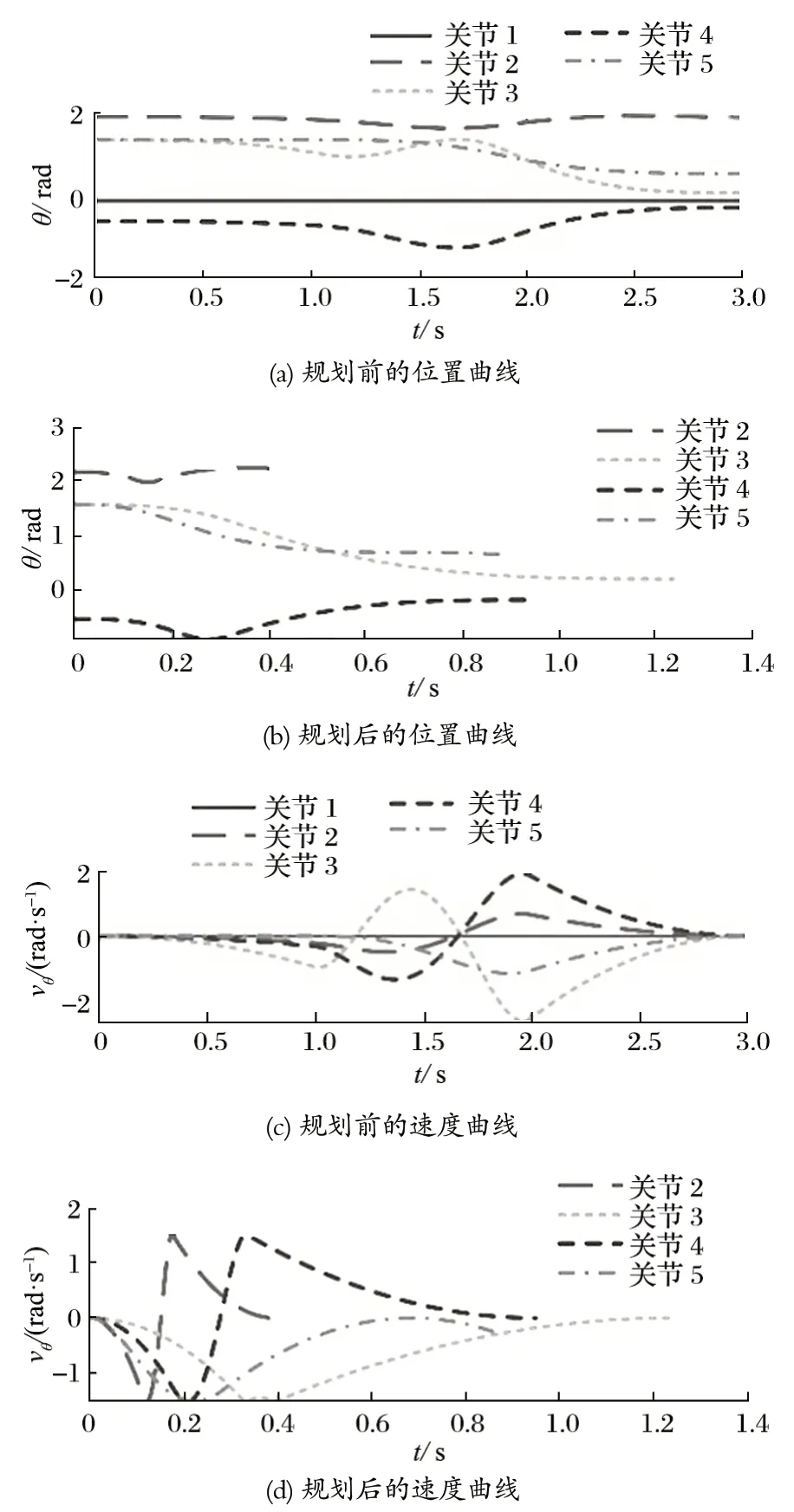
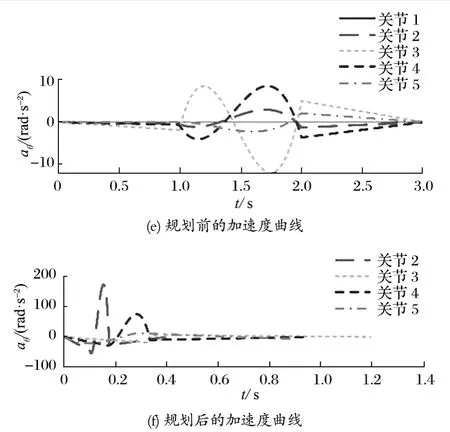
圖5 運動仿真軌跡曲線Fig.5 Motion simulation trajectory curve
經過粒子群算法的 100 次迭代,得到每個關節的運動軌跡,與之前相比,時間整體縮短。優化后末端到達指定位置時間為 0.89 s,比優化前縮短了 2.11 s,速度在 0.21 s 達到峰值 2.97 rad/s,更接近設置的最大速度 3 rad/s。相比之前加速度的跳變,優化后的加速度曲線連續,跳變幅度更小。
基于粒子群優化算法,以 3-5-3 多項式插值算法對三節臂進行規劃,其末端位置的軌跡如圖 6 所示。由圖 6 可以看出,曲線經過設定的 4 個位置,驗證了該方法的有效性。架管機三節臂的工作空間高度可達 2.2 m,滿足巷道架管的要求。
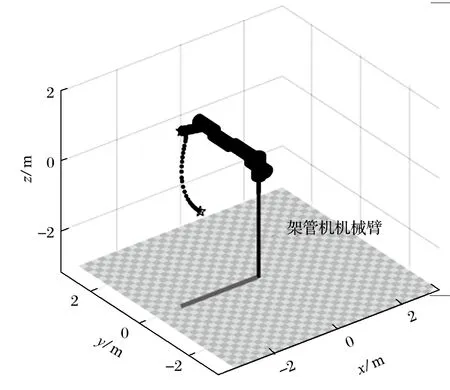
圖6 規劃后的軌跡Fig.6 Planned trajectory
4 結語
通過設計三節機械臂架管機,并對其進行運動學分析,運用粒子群算法對三節臂進行運動時間優化,得到了如下結論:通過軌跡規劃得到三節臂末端高度為 2.2 m,滿足巷道架管高度 1.7~2.6 m 的要求;通過 MATLAB 仿真得到三節臂的速度、加速度曲線,均滿足插值時間點的平滑過渡,能夠滿足三節臂各關節在速度約束下的運動平穩性,具有較好的實用性。

