SCS-CN模型在小流域產流計算中的應用

張曉涵，桑國慶

（濟南大學 水利與環境學院，山東 濟南 250022）

山洪是最嚴重的自然災害之一，山丘區小流域洪水徑流流速快、水量集中、滯時短，極易暴發局部洪災，且山洪具有很強的沖刷破壞力，會造成極端危害［1］。沂源縣是山東省平均海拔最高的縣，為典型的山區縣，洪澇威脅嚴重，特別是20世紀90年代以來極端天氣事件增多，經常發生集中暴雨，形成較大洪水，曾在1993年、1994年、1998年、2001年、2007年發生過較為嚴重的山洪災害。合理預測山丘區小流域洪峰是山洪災害預報預警重要的基礎工作和關鍵環節，深入研究小流域產流規律則是山洪洪峰計算的重要環節之一，也是一個非常重要的研究課題，現有的許多水文模型存在輸入參數多、參數獲取和率定比較困難等問題，美國農業部水土保持局于20世紀50年代開發的用于估算地表徑流量的徑流曲線數（SCS-CN）模型，結構簡單、所需參數較少、模擬結果準確度較高，能夠客觀反映土壤類型、土地利用方式及前期土壤含水量對降雨徑流的影響，被廣泛應用于地表徑流預測。

徑流曲線數C N值是SCS-CN模型中反映下墊面對產流過程影響的關鍵參數，其敏感性非常高。Boughton［2］的研究表明，徑流量Q隨平均濕潤狀況下CN值的變化而變化，CN值變化±10%，會導致徑流量變化±50%。李鑫川等［3］分析了SCS-CN模型參數的敏感性，各參數的總敏感性排序依次為：CN、b、λ（b為蓄水能力系數，λ為初損率）。劉賢趙等［4］應用SCS模型按照研究區集水區自然分水線劃分流域子單元，提出了適合黃土高原典型流域產流計算的CN值表。鄧景成等［5］利用模擬降雨資料應用平均值法等5種方法計算C N值，確定了不同流域的最優計算方法，證明了不同土地利用類型下CN值最優計算方法不同。初損率λ是SCS-CN模型的基礎參數，是降雨徑流過程初損值與最大潛在蓄水量的比值，是影響模型模擬精度的一個重要影響因素［6］。SCS-CN模型標準計算公式中λ采用了一個適用于美國北部地區的標準值0.2，實際應用中λ的取值存在區域性差異，標準值并不能完全適用于其他區域［7］。徐贊等［8］使用反算法、MATLAB結合粒子群算法優化黃土高原地區韭園溝流域初損率，并引入雨強因子修正徑流曲線法。張鈺嫻等［9］在對徑流曲線數模型參數λ敏感性分析的基礎上，應用實測降雨資料對參數λ與地表坡度關系進行了定量分析。王紅艷［10］研究表明當CN值一定時，初損率λ相對敏感性會隨著降雨量的增加而減小，尤其是在以農田草地為主的流域，對初損率λ取值最敏感。

筆者以沂源縣為研究區，根據土壤類型及土地利用類型確定沂源縣24個小流域的徑流曲線數CN值，根據小流域實測降雨徑流資料以Nash公式中的模型效率系數E、標準均方根誤差NRMSE、模型合格率作為判斷依據確定適合沂源縣的初損率λ，提高了模型徑流模擬精度，應用效果良好。

1 研究區域概況

沂源縣位于山東省淄博市最南端，處于東經117°48′—118°31′、北緯35°55′—36°23′之間。縣域東西長55.6 km，南北寬52.2 km，總面積1 636 km2。沂源縣是山東省平均海拔最高的縣，平均海拔400 m，海拔最高的魯山海拔為1 108 m，為山東第四高峰。域內地形復雜，地貌類型較多，主要有中山、低山、丘陵和山前傾斜平地幾種，東南沂河谷地海拔僅為180 m，中山、低山和丘陵面積占99.3%。沂源縣屬暖溫帶亞濕潤氣候區，四季分明，光照充足，雨熱同期。因山高谷深，小氣候明顯，降水變率較大，常發生春秋旱、夏澇的現象，降水主要集中在7—8月。境內大小河流共1 530條，呈樹枝狀分布。縣內河流分屬三大水系：沂河水系、汶河水系及彌河水系。沂源縣有大型水庫1座，中型水庫1座，小型水庫112座，沂源縣地形地貌及河流水系如圖1所示。

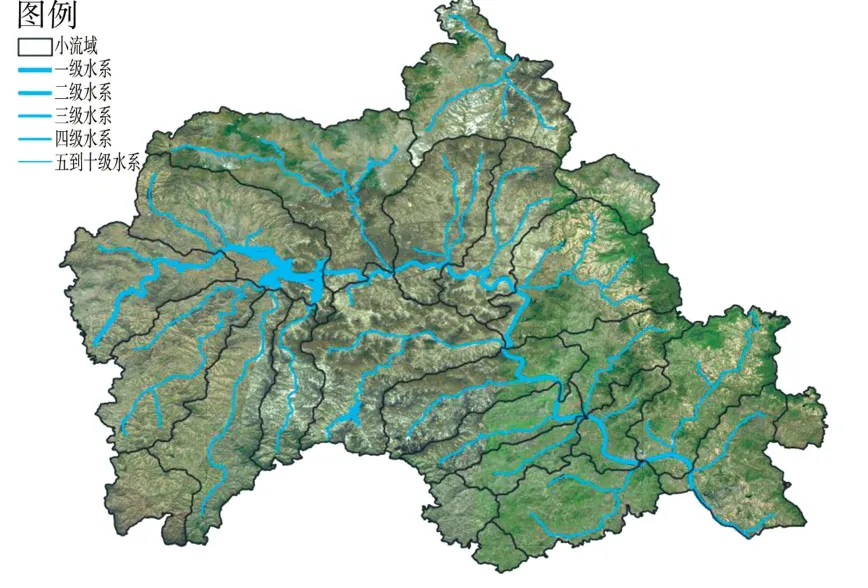
圖1 沂源縣地形地貌及河流水系

2 模型介紹及研究方法

2.1 SCS-CN模型介紹

SCS-CN模型是基于水量平衡方程和兩個基本假設提出的經驗模型。第一個假設：實際地表徑流量與最大潛在徑流量的比值等于實際入滲量與最大潛在蓄水量之比。第二個假設：初損量與最大潛在蓄水量成正比。

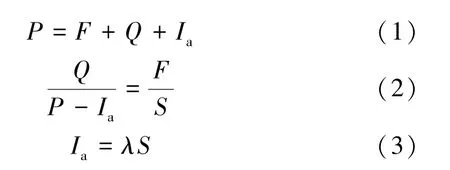
式中：Q為實際地表徑流深，mm；P為降雨量，mm；F為實際入滲量，mm；Ia為降雨初損量，包括產流前植被截留雨量、土壤表層蓄水量和蒸發量等，mm；λ為初損率；S為最大潛在蓄水量，是集水區吸收和截留暴雨降雨能力的度量，mm。

由式（1）～式（3）可以建立SCS-CN模型地表徑流量計算方程：

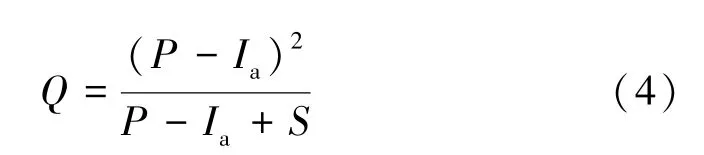
初損率λ受土地利用類型、植被截留、下滲等各種因素的綜合影響，一般取值范圍為［0～0.3］［11］。平均徑流條件下，SCS-CN模型中λ取標準值0.2，即Ia=0.2S，得到SCS-CN經典計算公式：

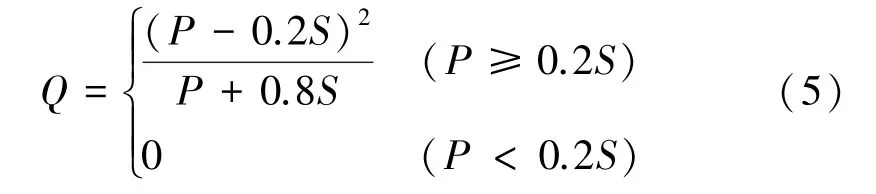
最大潛在蓄水量S為變量，其大小定性反映流域蓄水能力，且變化幅度可以很大，不便于取值，故引入無量綱的參數CN來推求S，S與CN值轉換關系如下：

徑流曲線數CN值是模型中用于描述降雨徑流關系的一個無量綱的重要參數，其作為下墊面（包括地形、地質、土壤、植被和土地利用方式等）綜合特征的定量描述，能夠反映不同下墊面類型的產流能力［12］。CN值理論上介于0～100之間，實際條件下取值范圍為30～98。CN值取決于土地利用現狀、水文、土壤類型及前期土壤濕潤程度。CN值越大，說明流域濕潤狀況越佳，地表的產流能力越強，地表蓄水量越小。CN=0時，S趨近于∞，表明降水全部下滲，地表無產流；CN=100時，S=0，表明流域無滲透，降雨全部轉化為地表產流［13］。

2.2 CN值確定方法

采用SCS-CN模型進行徑流模擬之前首先要確定參數CN值，CN值的確定方法分為查表法和反推法兩種。查表法［14］，即根據SCS提供的CN值檢索表基于土壤類型和土地利用確定CN值，該方法可能存在檢索表中無法查找到中國某些特殊土地利用類型的問題。反推法，即通過SCS產流公式反推CN值，根據降雨徑流實測資料率定CN值，主要包括平均值法、中值法、算術平均值法以及漸近線法，該方法需要研究區有一定年限的降雨徑流數據［15］。沂源縣小流域CN值采用查表法確定，并根據實測降雨徑流數據利用反推法進行區域合理性驗證。

查表法確定C N值首先要對流域土壤類型劃分水文土壤組，SCS-CN模型中根據土壤水分下滲能力和土壤質地結構劃分為A（透水）、B（較透水）、C（較不透水）、D（不透水）4類水文土壤組，見表1。

表1 水文土壤組［16］

通過查找CN值檢索表獲取研究區不同土地利用類型對應的CN值，運用ArcGIS軟件，將研究區土壤類型圖層和土地利用圖層利用地理處理中的相交工具進行疊加，生成土壤-土地利用圖層，該圖層每一區域內只含有一種土地利用類型和土壤類型信息，并在每個小區域屬性表中賦值其對應的CN值，最后通過對小流域內各小區域面積加權平均得到小流域CN值。

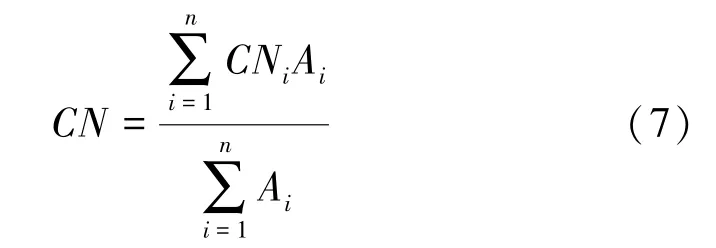
式中：CNi為土壤-土地利用圖層每個小區域對應的CN值；Ai為每個小區域的面積；n為劃分的小區域總數。

SCS-CN模型根據降雨前5 d的降雨量將前期土壤濕潤程度（AMC）從低到高劃分為三級：干旱（AMCI）、中等濕潤（AMCⅡ）及濕潤（AMCⅢ），見表2。

表2 前期土壤濕潤程度分級

三級前期土壤濕潤程度依次對應三種CN：CN1、CN2和CN3，CN1＜C N2＜CN3。查表法所得的CN值為CN2，可通過CN2求得CN1、CN3［17］。

由于反推法中的算術平均值法（利用實測降雨徑流數據求出S，再求每一個S對應的CN值，取CN值的平均值為最終結果）計算結果合格率最高［15］，因此本文通過比較算術平均值法得出的CN值與查表法求得的C N值相近程度來檢驗查表法在研究區的適用性。

2.3 初損率λ優化方法

由SCS-CN模型地表徑流量計算公式（式（4））可反推初損率λ的反算公式：

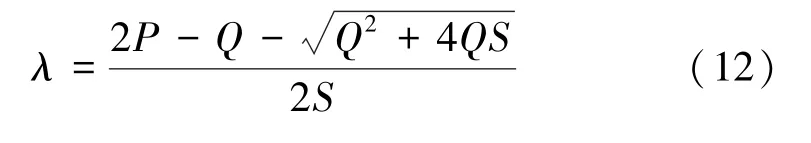
利用實測降雨徑流資料通過反算公式可求得研究區初損率λ的取值范圍，并計算變化范圍內不同λ取值（包括中值、平均值等）［18-19］下的模擬徑流深。本文以Nash公式中的模型效率系數E、標準均方根誤差NRMSE、模型合格率作為判斷依據。模型效率系數因其具有較好的檢驗能力被廣泛用于水文模型效率檢驗［20］，反映模擬值與實測值1∶1的線性接近程度，模型效率系數E的取值范圍為-∞～1，其值越接近1，表明模型的有效性越好，反之有效性越差。標準均方根誤差NRMSE用來衡量模擬徑流深與實測徑流深之間的偏差，NRMSE值越大代表誤差越大，模型精度越低。計算公式如下：

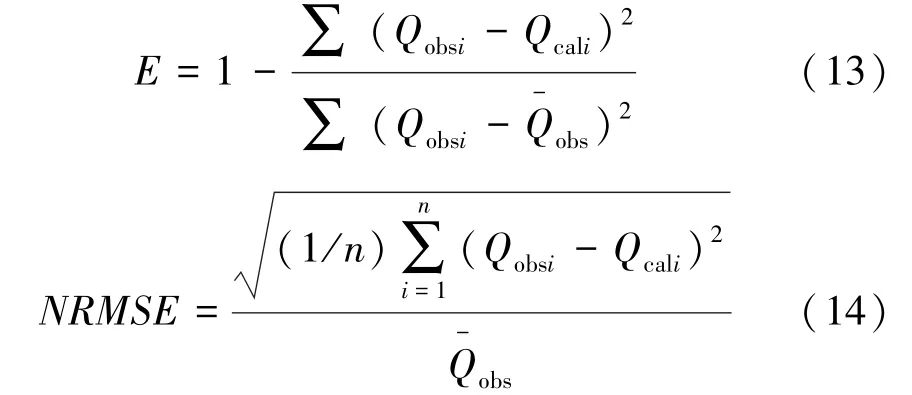
式中：Qobsi為實測徑流深，mm；Qcali為模擬徑流深，mm；obs為實測徑流深的平均值，mm；n為總事件數。

模型合格率是水文預報中常用指標之一，首先統計出模擬徑流深與實測徑流深絕對誤差≤2 mm或者相對誤差≤30%的降雨場次，然后將該降雨場次占總降雨場次的百分數作為模型計算的合格率。

3 應用實例

3.1 沂源縣小流域CN值確定

3.1.1 小流域C N值分布

沂源縣土壤類型主要分為砂壤土、黏壤土、砂黏壤土、粉壤土、砂黏土，其中砂壤土占50%左右。土地利用類型主要有耕地、林地、草地、房屋建筑區等，林地分布于沂源縣的北部、東部及中部地帶，如圖2和圖3所示。沂源縣土地利用類型見表3，沂源縣一年中干旱期較長，主要農作物為小麥、玉米，耕地蓄水能力較強，故水文條件取好；沼澤地長期受積水浸泡，持水性強，透水性弱，故水文條件取差（水文條件差指下滲少徑流多，水文條件好指下滲多徑流少）。沂源縣中等濕潤條件（AMCⅡ）下CN值見表4。

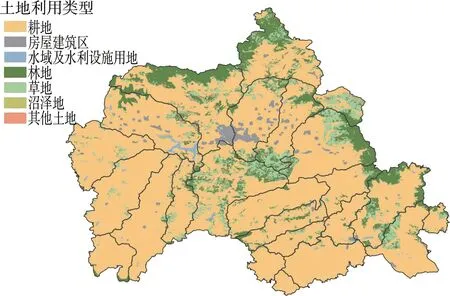
圖2 沂源縣土地利用類型分布

表3 沂源縣土地利用類型

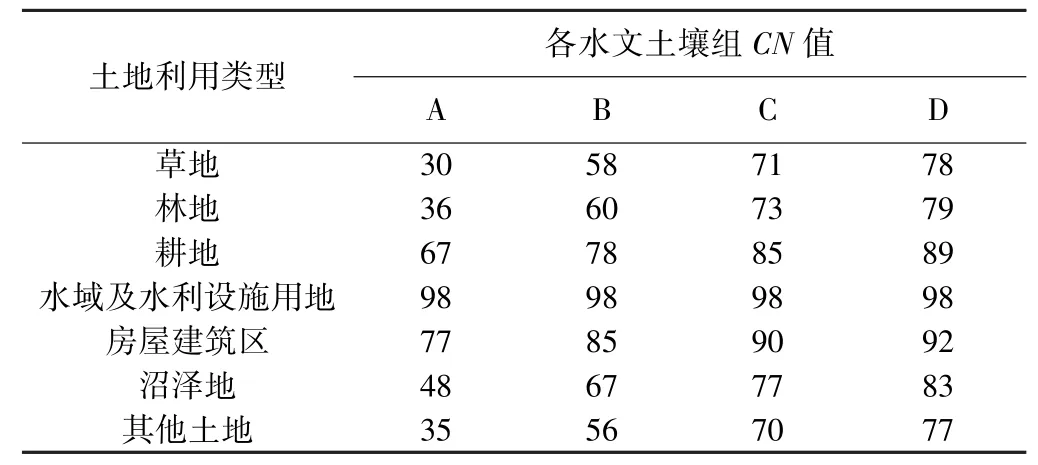
表4 沂源縣CN值

沂源縣共分為24個小流域，通過對小流域內各土壤-土地利用疊加小區域面積加權求得各個小流域CN值，取值范圍為52～82，其中較高CN值主要集中在沂源縣南部，小流域CN值分布如圖4所示。前期土壤濕潤程度為干旱和濕潤條件下的CN1、CN3可由式（8）和式（9）求得。

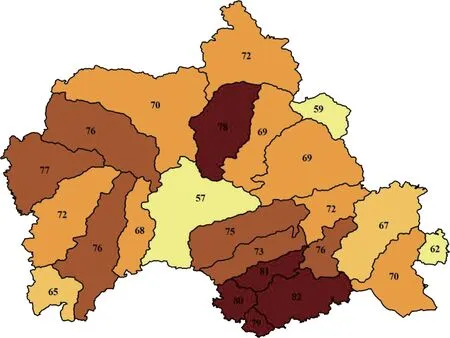
圖4 沂源縣小流域CN值分布

3.1.2CN值適用性驗證

本文用于驗證的實測降雨徑流數據來源于高村河流域的朱家莊測站，選取前期土壤濕潤程度為中等濕潤（AMCⅡ）的場次通過反推法中的算術平均法求得的CN2值為70，查表法得出的CN2值為68，因此認為查表法所求CN值可靠，可以用于沂源縣小流域。

3.2 初損率λ優化結果

本文選取沂源縣朱家莊水文站及雨量站27場降雨徑流數據用于初損率λ的優化，朱家莊測站位于高村河流域，控制流域面積31.4 km2，所在流域C N值為68，通過S與CN值轉換關系（式（6））可求得最大潛在蓄水量S為119.53 mm，根據場次降雨數據運用反算公式確定高村河流域初損率λ的變化范圍為0.05～0.50，平均值為0.20，中值為0.15，其中0.05～0.35的λ值約占85%，0.05～0.25的λ值約占66%，分別取λ=0.05、0.08、0.10、0.13、0.15、0.20、0.25、0.30，各場次降雨的模擬徑流深計算結果見表5，各λ取值下的評判指標見表6。其中參數λ取標準值0.20時，E=0.760 0，λ=0.13時模型效率系數最大、標準均方根誤差最小、合格率最高，故適合高村河小流域實際應用的初損率λ為0.13，亦可適用于沂源縣其他下墊面相似流域。

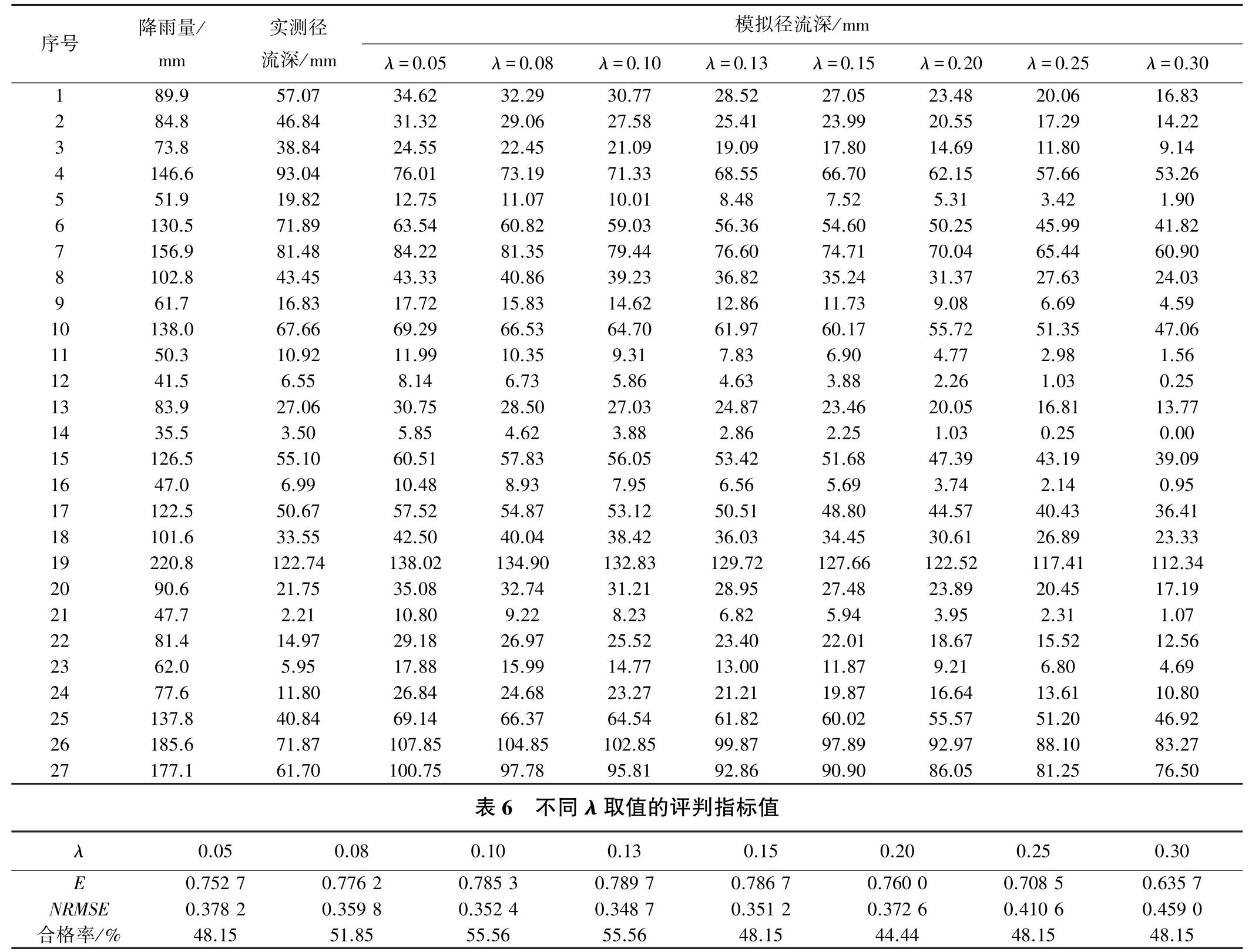
表5 不同λ取值的模擬值與實測值對比

4 結 論

（1）SCS-CN模型所需參數較少，初損率λ的取值直接影響模型模擬精度，研究可知λ取標準值并不能完全適用于沂源縣小流域，通過優化初損率λ，可以提高模型徑流模擬精度，更好地適用于沂源縣缺乏降雨資料的小流域降雨徑流模擬計算。

（2）通過對沂源縣24個小流域CN值的確定，可為小流域的SCS模型徑流預測提供參考。在實測降雨徑流資料充足的情況下還可以通過反推法求得CN值。

（3）初損率λ取標準值0.20時的模型效率系數為0.760 0，優化后的初損率λ取0.13，模型效率系數為0.789 7，模型運行效率只是部分提高，說明僅通過優化參數并不能顯著提高模型精度，模型要達到更高精度還需要考慮流域產流過程等其他區域性因素對徑流的影響。