模型認知下晶胞知識的教學建議

山東 劉樹領 周建國

晶體結構與性質是物質結構理論的重要組成部分，是培養學生證據推理與模型認知、宏觀辨識與微觀探析等化學學科核心素養的關鍵載體。由于該部分需要較強的抽象推理、空間想象及數學計算能力，因此，晶體知識是高中化學的難點。筆者利用各種教學備課、聽課活動及網絡平臺，將晶胞知識教學中采用的方法與措施進行歸納總結出相應的教學建議，以供各位老師參考。

1 當前晶胞知識教學的誤區

1.1 忽視晶胞等概念的教學

晶胞的結構與特點學習是晶體結構與性質的基礎，體現了結構決定性質的學科思想。只有掌握了晶胞概念及其結構特點，才能從晶體的微觀結構角度理解晶體的宏觀性質，了解晶體性能與用途改良的角度與方法。但在實際教學中，部分老師僅簡單直觀展示晶胞模型，讓學生記憶背誦結論。這種重結論輕過程的教學方法，使具有邏輯推理的化學知識成為零散的記憶知識，難以培養學生空間想象與推理的能力，造成學生遇到較為復雜的晶體堆積模型或非常規模型時無法解答問題。

1.2 忽視晶胞之間的關聯與轉化

晶體依據其粒子間的作用力分成了四大經典類型，但實際應用的晶體多是混合型的，如石墨晶體，因而學習晶體知識時，要注重知識的系統性、整體性和關聯性。實際教學中，許多老師把四種晶體類型嚴格分離出來，孤立地分析，通過記憶不同典型晶胞的結構特點解答各種常規題目。雖然這種教學方式得分率較高，但不能使學生深刻地理解晶胞的結構特點，一旦遇到非常規晶體結構時，則往往因無法靈活分析而無法作答。

【例1】鈷藍晶體結構如圖1所示。該立方晶胞由4個Ⅰ型和4個Ⅱ型小立方體構成，求晶體的化學式及密度。

圖1

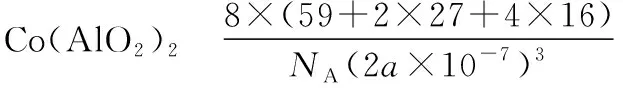
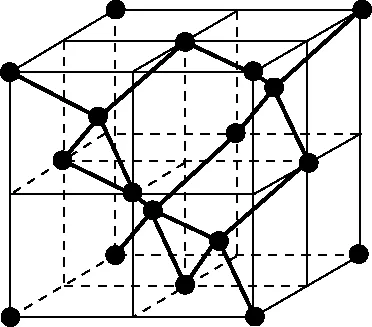
圖2

1.3 忽視數學知識在晶胞教學中的作用

化學反應原理、物質結構理論中涉及數學知識較多，如配位數、密度計算、空間利用率、空隙利用率等。在實際教學中，化學教師較少涉及立體幾何知識，忽略數學計算推理過程，導致學生處理晶體知識時心有余而力不足。若在數據基礎上，引導學生去思考數據是如何計算與得出的，則必然可提高學生分析解答問題的能力。

【例2】(2019·全國卷Ⅰ·35節選)圖3(a)是MgCu2的拉維斯結構，Mg以金剛石方式堆積，八面體空隙和半數的四面體空隙中，填入以四面體方式排列的Cu。圖(b)是沿立方格子對角面取得的截圖。可見，Cu原子之間最短距離x=________pm，Mg原子之間最短距離y=________pm。設阿伏加德羅常數的值為NA，則MgCu2的密度是________g·cm-3(列出計算表達式)。

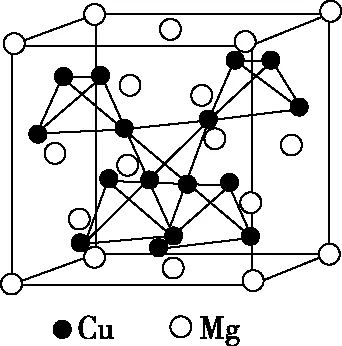
(a)

(b)

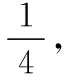
2 教學建議

2.1 重視晶胞概念教學，夯實晶胞特點知識

晶胞中有配位數、空間利用率、原子分數坐標、空隙利用率等概念，在晶體性質與結構知識學習中占有重要的地位，這些概念是建立在晶胞基礎知識的深度研究上，因此，學好晶體知識，必須先從晶胞的核心概念著手。

在教學中為了使學生理解晶胞的形狀及特點，首先讓學生利用常見的乒乓球、山楂或蘋果等實物模擬金屬原子的堆積方式，由下到上依次排列堆積4層，不難發現第1層堆積配位數為6的密置層或為4的非密置層，第2層中可出現多種堆積方式與第一層相切，依次進行第3、4層堆積，使學生在動手排列中感悟相切、空隙類型、最密堆積等概念及含義，然后運用多媒體展示金屬原子的堆積過程，學生通過觀察晶胞的抽取過程(圖4中的a、b、c、d所示)，從而理解晶胞概念及特點，即晶胞是按照三個維度進行無隙平移時不斷重復的結構單元，晶體由成千上萬個晶胞通過無隙排列堆積而成，即晶胞是代表晶體結構與性質的最小重復結構單元，同時掌握大部分晶胞具有平行六面體形狀及高度對稱性，如面對稱、棱對稱、點對稱，以及無隙并置等特點。

圖4a

圖4b

圖4c

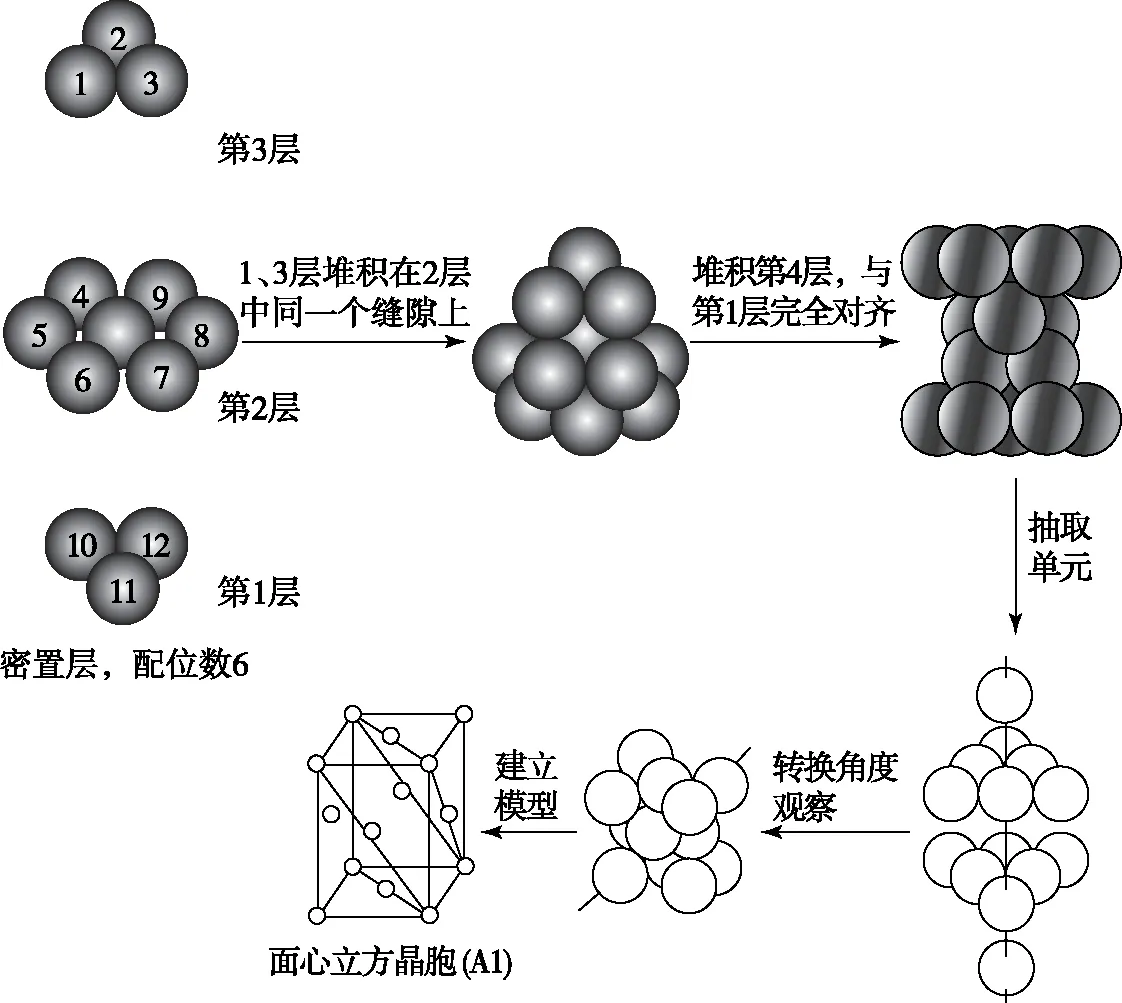
圖4d

2.2 重視對典型晶胞結構的深度分析

對典型晶胞模型的學習，切忌復述教材內容，應引導學生在充分理解晶體中粒子的位置關系、距離遠近、配位數多少、空間利用率高低等內容，提高學生空間想象、計算推理等能力。下面以教材中常見的氯化鈉晶胞模型為例，提出一系列問題來啟發學生思考。

(1)晶胞中含有鈉離子與氯離子的個數？(2)鈉離子、氯離子的配位數是多少？(3)已知晶胞邊長為apm，如何計算氯化鈉晶體密度？(4)如何利用晶胞邊長計算氯離子半徑？(5)因氯離子半徑大于鈉離子，故分析氯離子的堆積方式時，鈉離子是否位于氯離子圍成的空隙？(6)晶胞中氯離子(或鈉離子)的相對位置關系如何表示？(7)計算氯(或鈉)離子之間距離、鈉離子與氯離子之間的最短距離的方法是？(8)如何畫出晶胞的俯視圖(或主視圖等)(9)假若陽離子半徑增大，則氯離子之間是否還相切？如何判斷離子之間的相切關系？經過這樣的問題設計，避免了學生滿足于對現有典型晶胞結構特點的記憶，而是從更多的角度去分析晶體結構，進而提高解答實際問題的能力。

【例3】(2017·全國卷Ⅲ·35節選)MgO具有NaCl型結構(如圖5)，其中陰離子采用面心立方最密堆積方式，X射線衍射實驗測得MgO的晶胞參數為a=0.420 nm，則r(O2-) 為________nm。MnO也屬于NaCl型結構，晶胞參數為a′=0.448 nm，則r(Mn2+)為________nm。

圖5

【答案】0.148 0.076

2.3 運用模型與多媒體，提高學生空間想象能力

學生正處于直觀思維到抽象思維的轉化過程中，教師通過直觀模型、視頻或課件素材，有利于快速提升學生空間的想象能力。如在學習晶胞等概念時，可以展示晶胞的具體抽取過程。

【例4】如圖6(a)為SiO2晶胞中Si原子沿z軸方向在xy平面的投影圖(即俯視投影圖)，其中O原子略去，Si原子旁標注的數字表示每個Si原子位于z軸的高度，則原子A與原子B的距離是________。

圖6

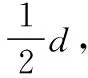
2.4 重視數學邏輯推理，培養學生思維的嚴密性與深刻性

晶胞中涉及的配位數、空間利用率、微粒之間的相切關系判斷等問題需要通過數學計算來解決，從而真正學會對晶體結構特點的分析與理解。

2.4.1 空間利用率問題

常以比較復雜的A3晶胞為例，引導學生進行具體推算，掌握對空間利用率的計算，具體過程如圖7所示。

圖7

【答案】74%

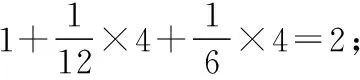
2.4.2 構成微粒之間的相切關系

在引導學生從能量最低原理角度來分析常見晶體為最密堆積方式(A1、A3)的前提下，啟發學生判斷微粒之間的位置關系，故以空隙填充為例，啟發學生從數學角度進行定量分析，以提高靈活解答實際問題的能力。

(1)正四面體空隙填充

設圖8中正四面體的堆積球半徑為R、空隙填充球半徑為r(以下同)，故根據余弦定理可列出(2R)2=2(R+r)2-2(R+r)2cos109.5°，進而解答r=0.225R，故空隙填充球半徑與堆積球半徑之比大于0.225時，則圍成正四面體的堆積球之間不再相切，而是堆積球與空隙球相切。

圖8

(2)正八面體空隙填充

根據勾股定理可列出2(R+r)2=(2R)2，進而解答r=0.414R，故空隙填充球半徑與堆積球半徑之比大于0.414時，則圍成正八面體的堆積球之間不再相切，而是堆積球與空隙球相切。

2.4.3 晶胞中粒子間距離與晶胞邊長(或對角線)之間的關系

晶胞中粒子間距除了引導學生從空間坐標位置(或原子坐標)角度去利用空間兩點間距離公式計算之外，還經常涉及其最短距離與晶胞邊長(或對角線)的等量關系，為避免學生死記硬背，故應引導學生利用數學知識給予證明，以提高圖像分析及空間想象能力。如金剛石晶胞(A4)中的等量關系。

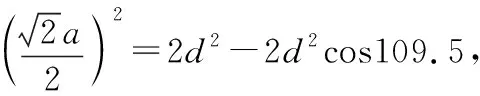
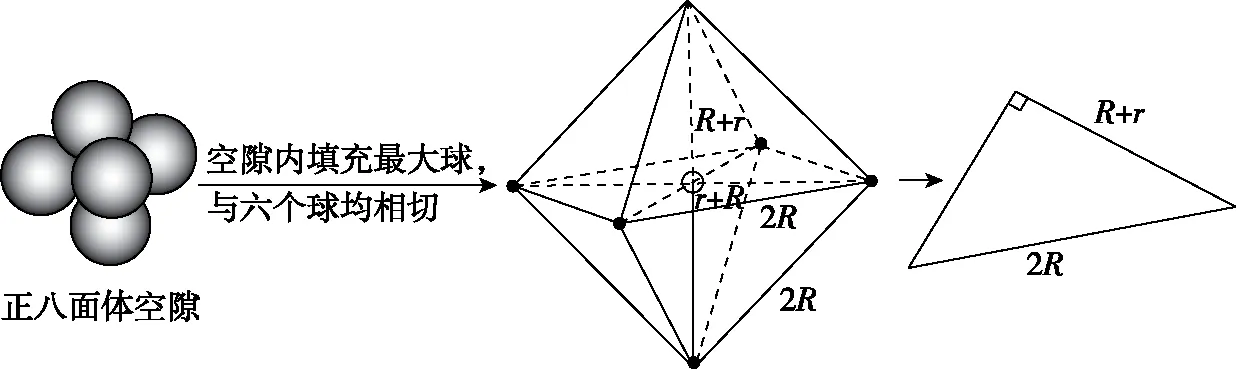
圖9

圖9

2.5 以點帶面，深耕細挖，提高思維靈活性

在講金屬常見的幾種晶胞時，以簡單立方晶胞為基點，進行一系列轉化：(1)若在立方晶胞的六個面心放上一個原子，得面心立方晶胞，由頂點原子相切變為頂點與面心原子相切，配位數也由6變為12；(2)若在立方晶胞的體心處放上一個原子，則可得體心立方晶胞，由頂點原子相切變為頂點與體心原子相切，其配位數由6變為8；(3)若體心立方晶胞的兩個對應面變形可轉化為六方最密晶胞，由頂點與體心原子相切變為三棱柱頂點與體心相切，配位數由8變為12，通過簡單立方晶胞與A1、A2、A3之間關聯起來，建立一個完整的系統，不僅培養了學生的空間想象能力，還可以對離子晶體、原子晶體、分子晶體的學習起指導作用。按照上述思路便可以把幾種典型的晶胞結構相結合，如圖10所示。

圖10

【例5】(2016·全國卷Ⅲ·37改編)GaAs為原子晶體，其晶胞結構如圖11所示，Ga和As的原子半徑分別為apm、bpm，設阿伏加德羅常數的值為NA，則GaAs晶胞中原子的體積占晶胞體積的百分率為________(列出計算式，可不化簡)。

圖11

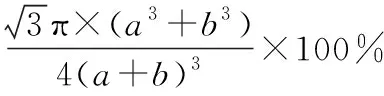
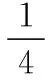
總之，晶體結構與性質的學習，離不開對晶胞等核心概念的熟悉與記憶，但更離不開數理邏輯推理的過程分析。只有真正掌握核心概念，正確運用模型認知及必要數理邏輯推理，才能提高學生空間想象能力、計算能力及跨學科知識的融合能力，使學生的證據推理與模型認知、宏觀辨識與微觀探析等化學學科核心素養得到較好的體現。