巖石物理相約束下的砂礫巖巖性粒級精細劃分
——以準噶爾盆地烏爾禾組為例
梁則亮,毛晨飛,肖華,陳國軍,高衍武,高明,張嘯
1.中國石油新疆油田分公司勘探開發研究院,新疆 烏魯木齊 836413 2.中國石油集團測井有限公司測井應用研究院,陜西 西安 710077
砂礫巖普遍具有近源、快速堆積的特點,其巖性變化較快,結構成熟度和成分成熟度普遍偏低[1,2],而且還保留了部分母巖的性質,其礫石成分、粒徑大小等因素綜合反映在測井曲線上,使得砂礫巖儲層普遍具有高密度、低聲波時差、高電阻率的特征,導致常規測井資料精細劃分砂礫巖巖性時的誤差較大,如在交會圖版中各巖性分布區間重疊度高,巖性精細劃分存在較大困難。
目前砂礫巖巖性判別的方法主要有以下幾種:趙寧等[3]、張永健等[4]基于巖性敏感曲線結合模型運算建立巖性識別圖版進行巖性劃分,該方法受限于重構曲線模型的準確度;袁照威等[5]、林香亮等[6]應用支持向量機、神經網絡和決策樹等模式識別算法進行巖性劃分,該類方法所需樣本較多,且模型分析及建立過程無法控制;羅興平等[7]、張明等[8]基于電成像測井圖圖像特征提取技術,采用圖像特征值進行巖性劃分,該方法雖然可以直接反映巖石顆粒形態特征,定性識別巖性,但電成像資料測量成本偏高,難以廣泛使用。因此,如何進一步深入挖掘常規測井曲線中包含的豐富巖性信息越來越受到研究人員的重視。
綜合前人研究思路,該研究以準噶爾盆地烏爾禾組實際測井資料、取心資料等數據為基礎,首次將巖石物理相分析技術與粒度中值曲線相結合,采用主成分分析、聚類分析、Fisher判別分析等數學方法,實現對巖性的初步劃分;再在巖石物理相約束下,結合粒度曲線對巖性粒級進行細分,建立了一種能夠有效劃分砂礫巖巖性粒級的方法。
1 研究區砂礫巖特征
準噶爾盆地烏爾禾組砂礫巖儲層粒度分布范圍廣、非均質性強(見圖1)。前人研究表明,不同粒徑的砂礫巖體,其物性、電性、含油性均存在較大差異[9],受粒徑變化影響,測井精細評價難以開展,且儲層電阻率主要受巖石粒徑影響,導致流體性質難以準確識別。該研究通過巖石物理相劃分結合粒度中值曲線實現巖性粒級的精細劃分,為后期測井精細評價等工作奠定基礎。

圖1 研究區JL20井儲層巖性圖
2 巖石物理相劃分
巖石物理相是指具有相似的巖石學特征、沉積-成巖作用特征及孔隙類型和結構特征等巖石物理性質的儲集層單元,是沉積、成巖、成藏和后期構造等作用的綜合效應[10-12]。因此,具有一組特定的測井參數值的巖石物理相所對應的巖性為同一類的概率是較大的。
2.1 主成分分析
首先采用主成分分析法將多條測井曲線轉化為少數幾個綜合的特征向量,使其盡可能多地反映巖性信息,并消除各特征向量之間的相關影響[13,14]。
首先采用零-均質規范化(Z-Score標準化)對測井曲線進行標準化處理,處理后的測井數據均值為0,標準差為1,公式如下:

(1)

進行主成分分析時,提取多少個主成分,應綜合考慮各主成分的貢獻率、累計貢獻率以及特征根的大小,一般取累計貢獻率達到85%~95%、特征根大于1的因子。在該研究中,綜合考慮累計貢獻率及特征根大小后,將提取的主成分數量確定為3個,累積貢獻率及特征根大小如表1所示,各主成分的系數矩陣如表2所示。
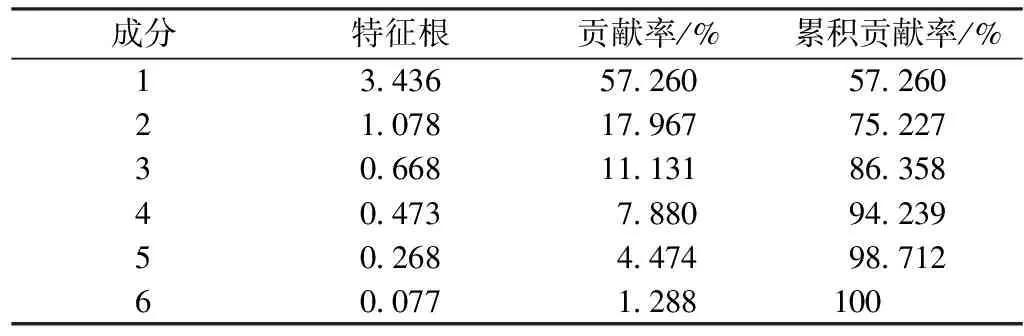
表1 主成分累計貢獻率
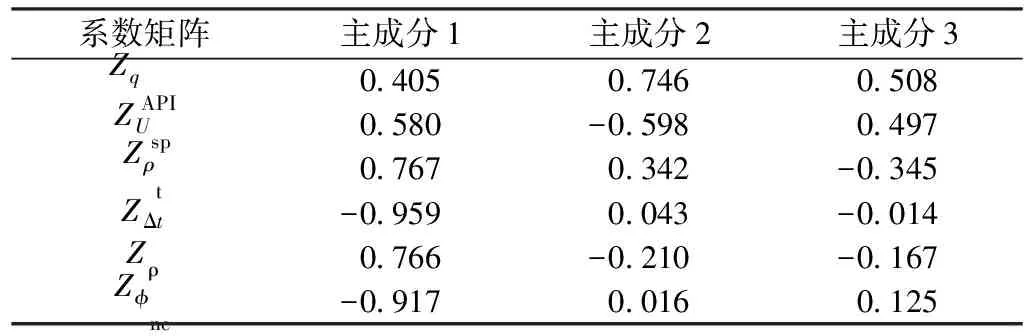
表2 主成分系數矩陣
各主成分值為標準化后的測井曲線值與其相應系數的乘積的累加,以主成分1為例,計算函數式為:
主成分1=0.405ZqAPI+0.580ZUsp+
0.767Zρt-0.959ZΔt+
0.766Zρ-0.917Zφnc
(2)
2.2 巖石物理相聚類劃分
目前主要的聚類分析方法有2種:系統聚類法和K-均值聚類法。由于K-均值聚類法具有高執行效率、可自行確定聚類數的優點,因此選取K-均值聚類法進行聚類分析,并對巖石物理相的聚類數進行優選[15]。
由于各樣本點到聚類中心的總距離減小的快慢在一定程度上可以反映出聚類數的合理性。因此,該次研究采用K-均值聚類法對提取的3個主成分進行聚類分析時,分別使聚類數K=3、4、5、…、10,然后分別計算不同聚類數下,各樣本點到聚類中心的總距離,可得到不同聚類數下樣本點到聚類中心總距離的變化情況圖(見圖2)。由圖2可知,隨著聚類數的增加,樣本點到聚類中心總距離的變化率逐漸降低,當聚類數為6時,其變化率接近于1。因此,確定最優巖石物理相的聚類數為6。
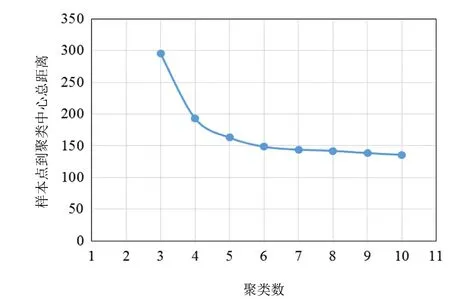
圖2 樣本點到聚類中心總距離隨聚類數的變化圖
表3為各巖石物理相的測井響應特征參數。巖石物理相2和巖石物理相3的自然伽馬平均值相近,分別為54.2117API和54.0739API,但其電阻率、密度、補償中子孔隙度平均值相差較為明顯;巖石物理相4和巖石物理相5的電阻率平均值分別為5.3845Ω·m和6.3098Ω·m,相差較小,但其自然伽馬、密度、補償中子孔隙度平均值相差較為明顯;巖石物理相1和巖石物理相2的自然伽馬平均值相差較大,分別為71.5851API和54.2117API,但兩者的電阻率、聲波時差、密度、補償中子孔隙度平均值差異性較小,測井響應特征區分度較低,如圖3所示。由圖3可知,巖石物理相1和巖石物理相2除自然伽馬外,其余測井曲線特征值分布區間及平均值均較為相近,且巖石物理相1具有高自然伽馬特征,因此認為巖石物理相1受高泥質含量影響,導致其他測井曲線響應特征不明顯,與巖石物理相2的測井響應特征分布區間發生重疊。
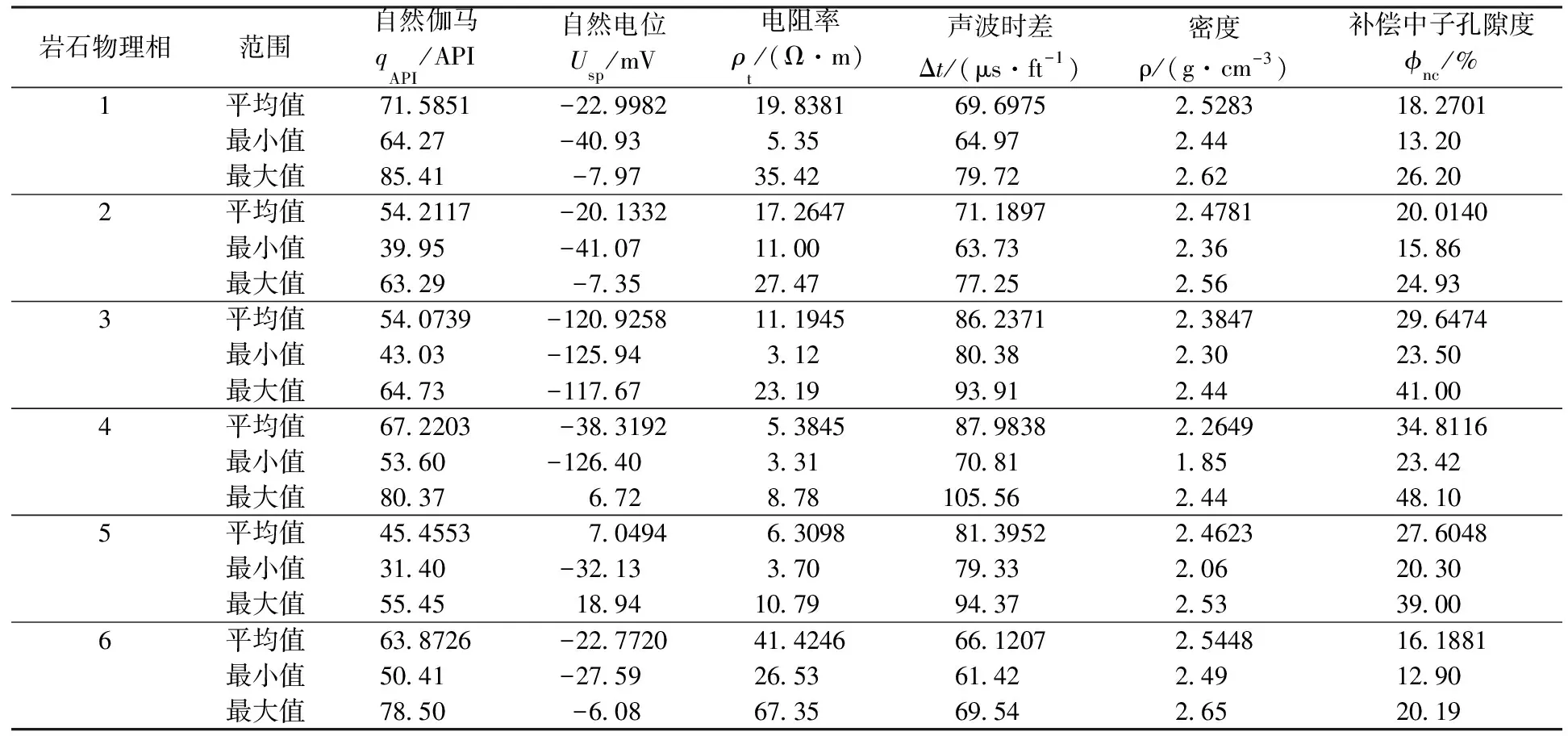
表3 各巖石物理相測井響應特征參數
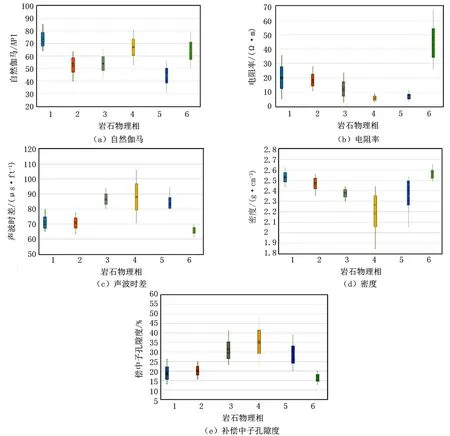
圖3 巖石物理相測井響應特征箱形圖
2.3 巖石物理相標定
為建立起巖石物理相與巖性之間的對應關系,以準噶爾盆地烏爾禾組的244個巖心樣品點的巖性描述為基礎,結合粒度分析定名結果,繪制巖性與巖石物理相的直方圖(見圖4)。由圖4分析發現,中礫巖主要以巖石物理相6為主,細礫巖主要以巖石物理相3為主,粗砂巖主要以巖石物理相5為主,中砂巖主要以巖石物理相2為主,泥巖主要以巖石物理相4為主;而細砂巖中所包含的各巖石物理相差別不大,但巖石物理相1相對較多,因此將巖石物理相1代表的主要巖性定為細砂巖。
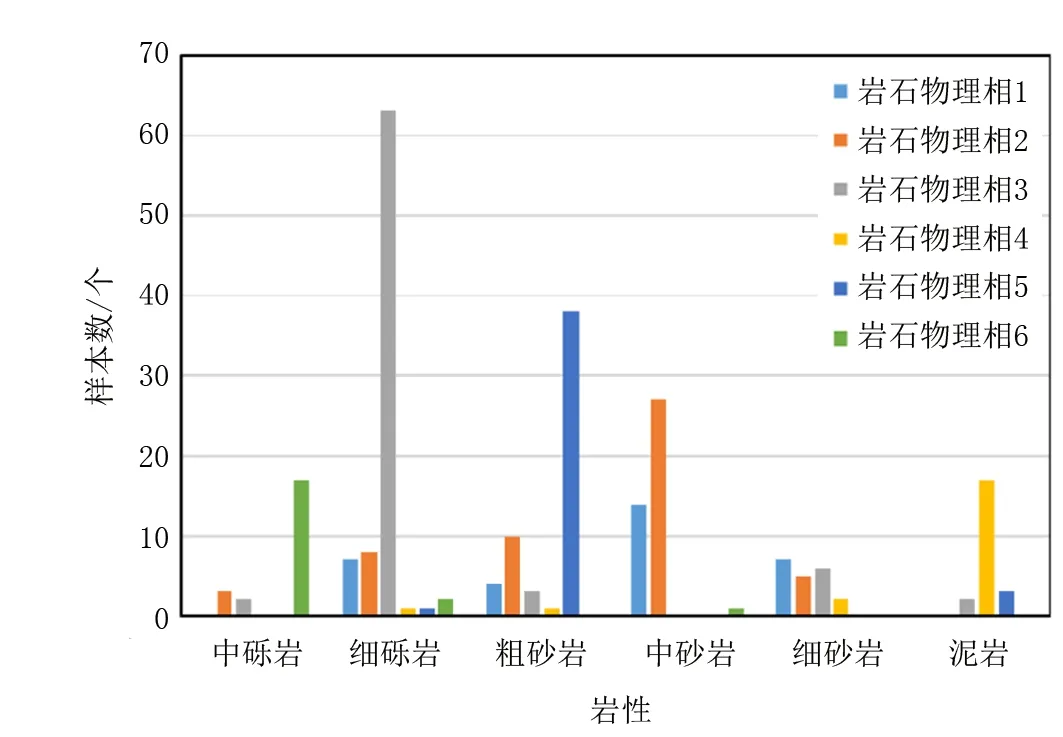
圖4 巖性與巖石物理相的柱狀圖
由圖4可知,各類巖石物理相與巖性并不是嚴格一一對應的,其中巖石物理相5代表的粗砂巖類別中,粗砂巖實際占比為90%;巖石物理相6代表的中礫巖類別中,中礫巖實際占比為85%;巖石物理相3代表的細礫巖類別中,細礫巖實際占比為83%;巖石物理相4代表的泥巖類別中,泥巖實際占比為81%;而巖石物理相1和巖石物理相2中,其代表的巖性實際占比均遠遠低于80%。因此,在巖性劃分過程中,巖石物理相1和巖石物理相2會使巖性劃分的誤差增大。因此,該次研究將進一步結合粒度分析數據,建立粒度參數計算模型,在巖石物理相1和巖石物理相2所代表的大類巖性約束下,進一步實現巖性細分。
2.4 巖石物理相判別方程建立
經過聚類分析后,巖石物理相劃分類別已經確定,但缺乏明確的判別公式,難以實現對單井儲層段的巖性劃分。為此,進一步采取Fisher判別分析法建立巖石物理相的判別方程。
圖5為Fisher判別分析運算后得到的典則判別函數散點圖,可以看到巖石物理相1和巖石物理相2的組質心相近,分布區間重疊度高,與巖石物理相1和巖石物理相2的測井響應分布特征相一致。

圖5 Fisher判別分析散點圖
運用Fisher判別分析法建立的研究區巖石物理相判別函數計算公式如下:
Fn=anqAPI+bnUsp+cnρt+dnΔt+enρ+fnφnc+gn
(3)
式中:Fn為各巖石物理相的判別函數計算值;n=1、2、…、6,分別對應巖石物理相1、巖石物理相2、…、巖石物理相6;an、bn、cn、dn、en、fn分別為各巖石物理相判別函數中每條曲線對應的系數;gn為各巖石物理相判別函數的常數項。Fisher判別函數系數如表4所示。
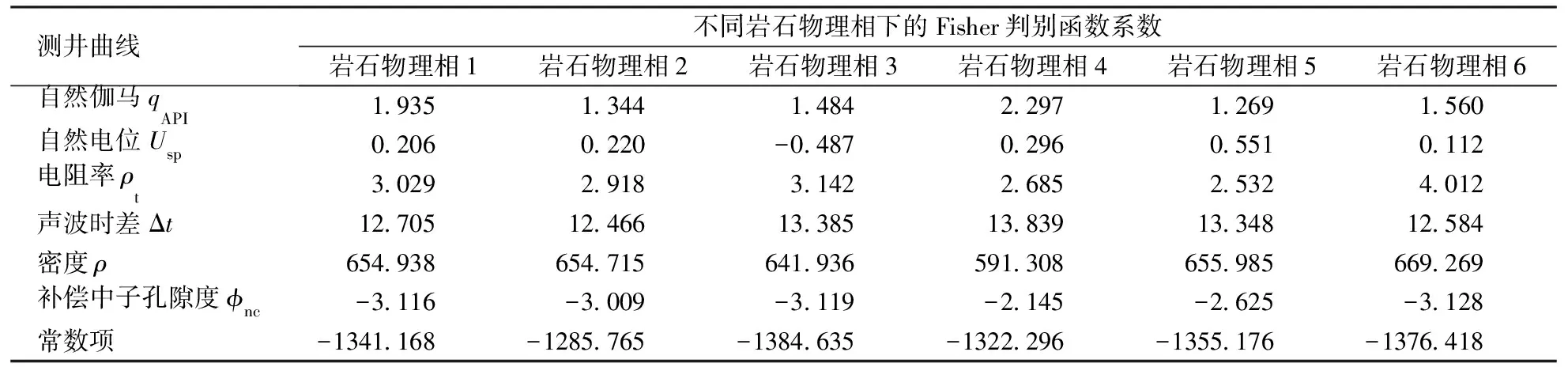
表4 Fisher判別函數系數
對未知巖性進行判別時,把該層段對應的測井曲線數值分別代入各巖石物理相的判別函數中進行計算,根據最大似然原則,計算得到的哪個巖石物理相判別函數得分最高,則該層段就歸屬于哪個巖石物理相。
為檢驗該判別模型的準確性,對研究區聚類分析劃分出的巖石物理相分類數據進行回判,判別結果如表5所示。
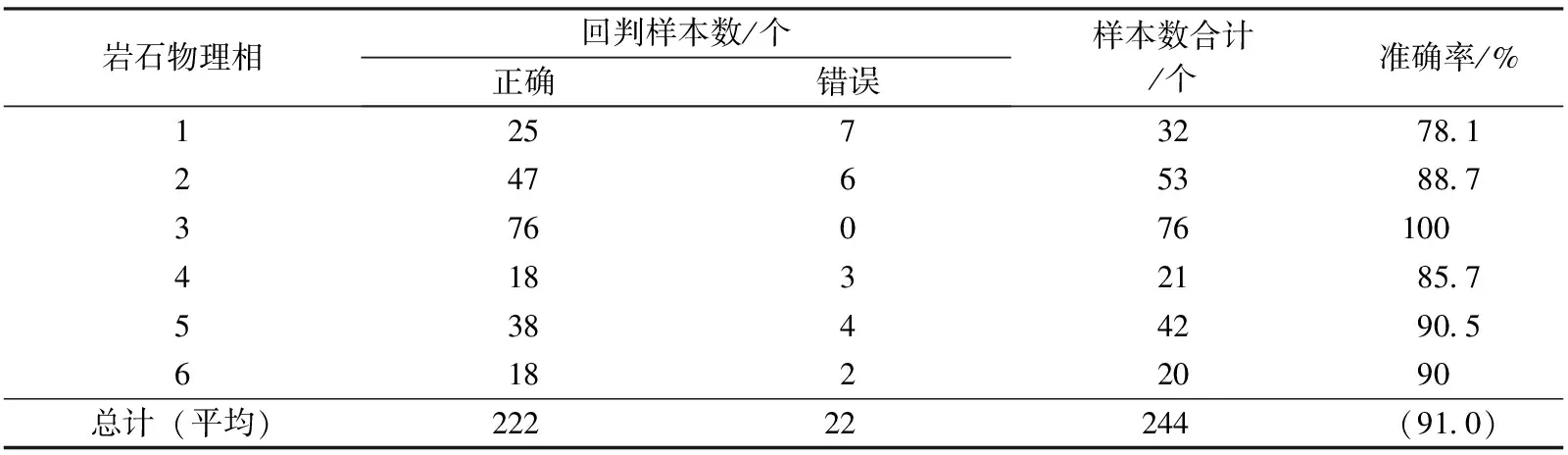
表5 Fisher模型回判結果統計表
總體來看,誤判主要出現在巖石物理相1和巖石物理相2的識別中,該結果與測井響應特征分析結果一致,這2類巖石物理相除自然伽馬外,其他測井曲線響應特征分布區間相似度較高,導致Fisher判別法識別出現誤判。巖石物理相4由于樣本數較少,個別樣本出現誤判時對總體準確率影響較大,導致該類樣本識別準確率偏低。
3 粒度參數的計算及模型建立
前人研究認為粒度中值在描述濁流相、河流相等碎屑巖巖性時具有一定代表性[16,17],為此,研究在巖石物理相1和巖石物理相2代表巖性的約束下,進一步建立粒度中值計算模型,實現巖性的精細劃分。
在各類測井曲線中,自然伽馬測井曲線值主要受沉積物泥質含量、分選性和粒度變化的影響,因此該條測井曲線被廣泛應用于泥質含量的計算中,而“泥質”是一種粒度概念,即自然伽馬與粒度之間應有一定的聯系。考慮到實際地質狀況的復雜性,采用單一自然伽馬建立的粒度中值計算模型受到的影響因素較多,可靠性較差。在綜合對比分析后,選取自然伽馬曲線與電阻率曲線進行多元回歸分析,建立粒度中值(采用對數粒級表示,粒度中值=-log2D,D為粒徑)與自然伽馬、電阻率的關系模型:
計算粒度中值=0.05×qAPI-0.09×ρt-0.706
(4)
為了檢驗回歸公式的模型精度,將研究區4口井取心段粒度分析得到的粒度中值與測井計算得到的粒度中值進行對比分析,結果如圖6所示。圖6所示數據表明,計算粒度中值與分析粒度中值符合度較高,證明了該粒度中值計算模型的可靠性。
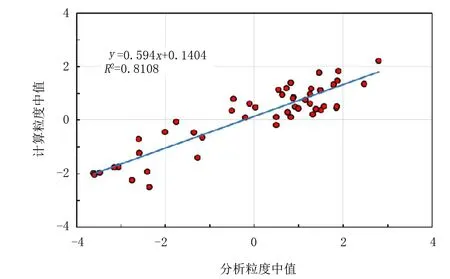
圖6 計算粒度中值與分析粒度中值交會圖
用上述粒度中值模型對J206井進行計算,效果如圖7所示,計算粒度中值與分析粒度中值符合度較高,且曲線變化趨勢大體一致,進一步說明粒度中值曲線劃分巖性的可靠性。但受限于模型精度產生的計算誤差影響和不同巖性粒度中值分布區間難以準確劃分的影響,單獨采用粒度中值劃分巖性的可靠性較低,因此筆者借助粒度中值曲線相對值對巖石物理相1和巖石物理相2的代表巖性進行進一步識別。

注:dh為井徑;ρlld為深側向電阻率;ρlls為淺側向電阻率。
4 巖石物理相約束下的巖性粒級劃分效果
根據研究區巖石物理相與巖性分類統計結果對比分析發現,巖石物理相1與巖石物理相2中包含的主要巖性分別為細砂巖、中砂巖、粗砂巖、細礫巖,上述4類巖性占巖石物理相1與巖石物理相2樣本數的97.5%;再結合巖石物理相1與巖石物理相2的粒度中值曲線變化情況,可將巖性按以下粒度中值變化范圍進一步劃分:細砂巖,粒度中值≥1.5;中砂巖,1≤粒度中值<1.5;粗砂巖,0.5≤粒度中值<1;細礫巖,粒度中值≤0.5。
圖8是該研究區J206井某一層段取心巖性剖面、錄井巖性剖面與運用筆者所提出的巖石物理相與粒度中值相結合的巖性粒級劃分方法確定的巖性剖面對比圖。由圖8可知,巖性較粗的粗砂巖、細礫巖、中礫巖段(圖8中②、③、④)完全對應,泥巖段(圖8中①)基本對應,在中-細砂巖段(圖8中⑤、⑥)存在少許差異,巖性劃分符合率如表6所示,總體符合率為88.9%,證明運用該方法進行巖性精細劃分是可靠的。

表6 研究區J206井巖性劃分符合情況統計表

圖8 研究區J206井巖性綜合劃分成果圖
5 結論
1)結合聚類分析、Fisher判別分析等方法進行巖石物理相劃分后,再根據粒度分析巖性與巖石物理相的統計關系,對巖石物理相進行標定,實現了研究區巖性的識別劃分,但巖石物理相1與巖石物理相2標定效果較差。
2)沉積巖粒度中值的變化范圍和規律可以反映巖性的粗細與結構。該研究采用自然伽馬曲線與電阻率曲線,建立了粒度中值計算模型,結合巖性判別函數,對識別效果較差的巖石物理相1與巖石物理相2的巖性進行了進一步的精確劃分。劃分結果與巖心描述巖性符合度較高,證實了該方法劃分巖性的可靠性。

