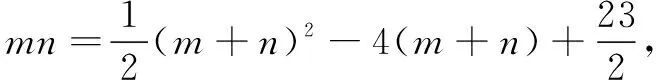中考二次函數模型試題的源與流
石樹偉 (江蘇省揚州市廣陵區教師發展中心 225006)
無論是知識的綜合性還是思維的層次性,二次函數都當之無愧地占據著初中數與代數領域的“制高點”,是肩負區分功能的中考壓軸題的命題熱點.當前,二次函數試題多為“拋物線外衣+幾何內核”的命題方式,即以拋物線為背景,將二次函數與三角形、四邊形、圓等知識結合起來考查學生的綜合應用能力,這樣的考查方式“人為拼湊”痕跡嚴重,掐頭去尾燒中段,對二次函數的來源和應用關注不夠,偏離二次函數內容的課標要求,對數學建模核心素養的考查缺失.因此,二次函數模型試題應運而生,越來越成為考查熱點.
1 認識二次函數模型試題
1.1 從一道試題說起
例1(2013江蘇揚州)如圖1,在梯形ABCD中,AB∥CD,∠B=90°,AB=2,CD=1,BC=m,P為線段BC上的一動點,且和B,C不重合,連結PA,過P作PE⊥PA交CD所在直線于E.

圖1
(1)在圖1中找出一對相似三角形,并說明理由;(2)若點P在線段BC上運動時,點E總在線段CD上,求m的取值范圍.

1.2 二次函數模型試題及其考查思路
例1在題目中根本沒有出現任何“函數”或“二次函數”之類的字眼,但最終卻是用二次函數來解決問題.因為需要學生自己構造二次函數,我們把這類試題稱為二次函數模型試題.二次函數模型試題與一般的二次函數試題不同,它關注了二次函數的來源與應用,有利于考查學生的數學建模素養和應用意識.
二次函數模型試題考查的基本思路如圖2所示,一般要設計一個現實情境(生活現實或數學現實),因為只有在現實情境中才能考查一個學生“用數學眼光觀察現實世界,用數學思維思考現實世界,用數學語言表達現實世界”[1]的能力;一般避免通過小題鋪墊來指令學生先構造函數,再利用函數解決問題,而是需要學生自主發現現實情境中存在函數依賴關系,從而自主構造函數,自覺應用函數解決問題.這里強調自主自覺,是因為當學生未來遇到真正的實際問題時,不會再有人告訴他“這個問題里面有函數關系”,或有人替他分解成幾個小問題,指令他構造函數.強調自主自覺才能真正考查學生的函數建模意識和能力[2].

圖2
2 二次函數模型的源
二次函數模型試題需要學生自主發現函數關系、自主建構二次函數,因此,要想順利解答二次函數模型試題,首先需了解二次函數模型的一般來路.
2.1 如何想到構造二次函數?
二次函數要靠我們自己發現、自主構造,那怎么想到要去構造函數呢?二次函數模型試題,雖然題目中不會直接指令或提示構造函數,但也不是完全無跡可尋,一般從以下兩個層面啟示我們要構造函數.
2.1.1顯性層面
顯性層面,如果試題已知情境問題的最值或研究其最值,可以啟示我們想到函數,從而主動構造函數去解決問題.如下面的例2求最大面積,啟示學生構造二次函數解決問題.

圖3
例2如圖3,要用總長為16 m的籬笆,一面靠墻(墻的可利用長度為6 m),圍成一個長方形的生物園飼養小兔,求小兔活動范圍的最大面積.
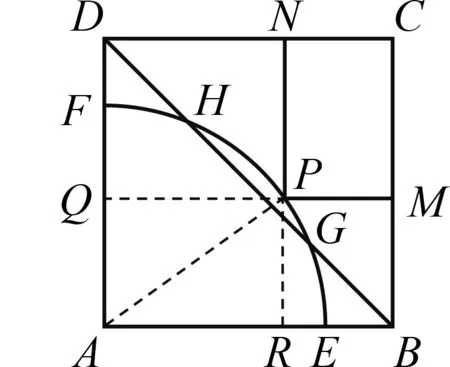
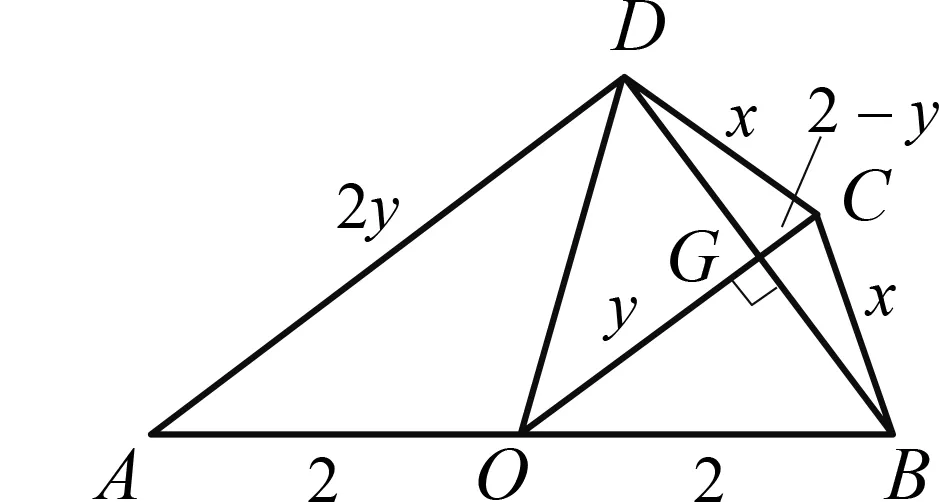
分析 本題求最大面積,容易聯想到構造二次函數解決問題.設生物園面積為S,寬AB=x,則長BC=16-2x,利用長方形面積公式可得S=x(16-2x)=-2(x-4)2+32.又因為0 顯性層面,如果試題已知情境問題的增減性或研究其增減性,也可以啟示我們想到函數,從而主動構造函數去解決問題.如下面的例3,“30天內利潤隨天數t的增大而增大”,這是已知“利潤-天數”函數的增減性情況,啟示學生構造函數解決問題. 例3(2016江蘇揚州)某電商銷售一款夏季時裝,進價40元/件,售價110元/件,每天銷售20件,每銷售一件需繳納電商平臺推廣費用a元(a>0).未來30天,這款時裝將開展“每天降價1元”的夏令促銷活動,即從第1天起每天的單價均比前一天降1元.通過市場調研發現,該時裝單價每降1元,每天銷量增加4件.在這30天內,要使每天繳納電商平臺推廣費用后的利潤隨天數t(t為正整數)的增大而增大,a的取值范圍應為. 2.1.2隱性層面 有的試題雖然沒有出現任何提及“函數”的字眼,也沒有最值、增減性等方面的顯性提示,但通過對問題情境的分析,發現其中蘊含著函數的三個要素:一是在一個運動變化過程中,二是有兩個變量,三是一個變量隨著另一個變量的變化而變化.由此可以啟示我們想到函數,從而主動構造函數去解決問題.如例1是一個點P從點B運動至點C的變化過程,其中BP,CE是變量,且CE隨著BP的變化而變化,這就說明CE與BP之間存在著函數關系.這樣的函數考查有利于學生充分感悟函數概念的本質,可以讓學生體會到函數來源于運動變化過程中變量之間的依賴關系,感悟到函數是研究運動變化過程的有效模型.再如下面的例4. 圖4 (1)當n=1時,①求線段AB所在直線的函數表達式;②你完全同意小明的說法嗎?若完全同意,請說明理由;若不完全同意,也請說明理由,并求出正確的k的最小值和最大值. (2)若小明的說法完全正確,求n的取值范圍. 想到函數了,如何構造函數呢?二次函數的構造,關鍵在于“二次”如何得到,一般有以下三個途徑. 2.2.1乘法模型——一次乘一次得二次 乘法模型“一次乘一次得二次”常見的問題情境有:①面積問題,矩形面積=長×寬,三角形面積=底×高÷2,如果長、寬或底、高都能用含有自變量的一次式表示,則容易得到關于自變量的二次式,如 例2;②銷售問題,總價=單價×銷量,總利潤= 單件利潤×銷量,若單價、銷量或單件利潤、銷量都能用含有自變量的一次式表示,則容易得到關于自變量的二次式,如例3;③相似問題,相似三角形對應邊成比例,若比例外項或比例內項都能用含自變量的一次式表示,則容易得到關于自變量的二次式,如例1;④其他蘊含乘法數量關系的問題,如例4中反比例函數的系數k=動點橫坐標×縱坐標. 2.2.2幾何模型——運用勾股定理得二次 幾何模型“運用勾股定理得二次”常見的問題情境有以下兩種: ①一個直角三角形,先用含有自變量的一次式表示各邊,然后運用勾股定理得到一個等式,最后展開變形得二次函數,如下面的例5. 圖5 (1)若四邊形PMCN的面積為3.5,求四邊形PMCN的周長; (2)求四邊形PMCN面積的最小值,并說明此時點P的位置. ②兩個共邊直角三角形,先用含有自變量的一次式表示其余各邊,然后在兩個直角三角形內分別運用勾股定理表示出共邊的平方(算兩次),得到一個等式,最后展開變形得二次函數,如下面的例6. 圖6 例6(2020江蘇揚州)如圖6,已知點O在四邊形ABCD的邊AB上,且OA=OB=OC=OD=2,OC平分∠BOD,與BD交于點G,AC分別與BD,OD交于點E,F. 分析 第(1)題易由基本圖形“等腰三角形(△OAD)+頂角外角平分線(OC平分∠BOD)”得到OC∥AD,也易由三角形中位線定理(OG是△BAD的中位線)得到OC∥AD. 圖7 2.2.3組合模型——多個已知函數組合得二次函數 (1)當科研所到宿舍樓的距離x=9 km時,防輻射費y=萬元;a=,b=; (2)若每公里修路的費用為90萬元,求當科研所到宿舍樓的距離為多少千米時,配套工程費最少?(3)略. 構造出二次函數關系式不是最終目的,最終目的是為了應用二次函數去解決問題.因此,要想完整解答二次函數模型試題,還需要把握二次函數模型的一般去路. 二次函數模型試題構造出二次函數后,一般應用所構造的二次函數研究以下三類問題.需要注意的是,研究每一類問題都需結合大致圖象,即數形結合. 3.1.1研究最值問題 最值問題有三種情況: ①頂點最值,即圖象頂點在自變量取值范圍內,頂點縱坐標即為函數最值,如例4第(1)題、例5、例6、例7; ②區間最值,即圖象頂點不在自變量取值范圍內,需結合圖象確定最值,如例2; ③離散最值,即函數圖象不是連續拋物線,而是一系列的散點,需結合圖象根據散點到對稱軸的距離遠近確定最值. 3.1.2研究增減性問題 增減性問題有兩種情況: ①連續拋物線,所有點要保持統一的變化趨勢,一般無需考慮跨對稱軸的情況,如例4第(2)題; ②離散拋物線,所有點要保持統一的變化趨勢,最后一點或第一點可以跨對稱軸,與其余各點分置于對稱軸的兩側,但跨對稱軸的那一點必須最接近對稱軸,如例3. 3.1.3研究參數范圍問題 這一類問題與前面兩類問題有交叉.含參數的二次函數解析式,既含自變量又含參數,因此不能利用它去列不等式求參數范圍.一般需表示出它的最值或對稱軸,這樣就剝離了自變量,僅保留參數,然后再根據已知條件,利用最值或對稱軸的范圍列不等式求出參數范圍,如例1、例4第(2)題. 3.2.1整體的眼光 3.2.2轉化的思想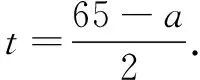


2.2 如何構造二次函數?



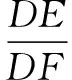
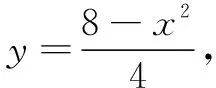
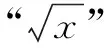


3 二次函數模型的流
3.1 構造的二次函數一般用來干什么?
3.2 構造的二次函數一般有哪些變形?