數形結合思想在初中數學解題中的應用

韓 軍

(甘肅省靖遠縣高灣中學 730600)

數形結合通常指在數學信息不發生改變的情況下，數據與圖形的有效轉換，將相關數據精密的呈現在圖形上，以圖形上出現的變化，對數據變化進行理解，并經過數據了解到圖形的狀態.因此，在對數學問題進行解決時，需注重圖形與數值的有效結合，以促使學生通過眼睛觀看到數據的變化，這不僅能夠使學生對于數學知識的學習興趣得以提高，而且還能使數學問題更為簡單，促進學生有效解決相關數學問題，從而使學生形成良好的學習與思考習慣.初中階段的數學解題中，教師可通過相應的教學方法對學生的學習習慣進行培養，以促使學生形成相應的自學能力.基于此，數學教師在解題教學中，需注重數形結合的思想融入，促進學生對于數學知識的理解，以數形結合的思想解決相關應用題，以此為數學學科的實踐問題解決奠定夯實的基礎，并促進學生自身的水平提高.同時，數形結合還有助于學生的理解力以及邏輯能力的提高，引導學生由數學題目中找到可應用的內容，以畫圖表達出內容，以實現數學題的簡單化、明了化，以實現數學題的有效解決.

1 數形結合思想及其思維培養的意義

1.1 數形結合思想概述

數形結合運用到的是數和形的對應關系，其能夠使數與形之間實現有效轉換，以便于數學難題的有效解決，許多問題都能通過該原理，獲得更為便捷的解題方式，許多的數學知識都抽象無法有效理解，如能通過數形的有效轉化，就更便于理解，屬于初中數學實際解題中的重要思想.通過數形結合思想的運用，主要是對條件與結論之間的聯系進行考察，將其聯系通過圖形或數軸實施表達，不僅能通過幾何與代數實現數學問題的解決，而且還能使解題的效率與準確率得到有效提高.

1.2 數形結合思維培養的意義

首先，有助于學生直覺思維的發展.對于直覺思維而言，其主要指不通過嚴格邏輯推理的過程，在第一時間對數學問題做出合理猜測與設想，直到數學問題的解決，其并非是毫無根據的，而是來源于新舊知識的聯系、銜接與積累.通過直覺思維實現問題解決，就需做到認真觀察、猜測、聯想與歸納.而數形結合的思維培養，則需學生形成相應的自覺思維，需學生在較短的時間實現幾何模型的構建，依據給出的已知條件，實現函數或者幾何圖形的構造，以實現數學問題的直觀形象的解決.

其次，有助于學生學習數學知識的興趣提高.初中數學的解題過程中，對學生而言是極為枯燥的，且涉及到一定的思維與邏輯，具有較大的難度，這就會影響到學生對于數學知識的學習興趣.想要避免該現象出現，數學教師在解題教學中，就需通過數形結合的思想，將數學題和圖形有效結合，以促進學生學習興趣提高的同時，吸引學生的學習注意力，促進學生對于數學知識的學習難度降低，以促使學生積極主動接受數學知識的同時，促進學生自身的學習能力提高.

2 數形結合在初中數學解題教學中的問題

2.1 對數形結合的方法缺乏重視

經過調查顯示，數形結合在初中數學的解題中沒有得到充足的重視.由此可知，數形結合普及，不僅需教師自身具備相應的數形結合意識，而且還需創設出通過數形結合的方法進行問題解決的環境，且學生也需充分的認識與了解到數形結合在解題中的重要性.

2.2 對數形結合的價值缺乏認識

初中數學的傳統化學習中，學生對于數學知識的學習較為吃力，這就使學生無法充分了解到何為數形結合，無法通過數形結合的靈活運用，促進數學問題的解決，也無法了解到數形結合的簡便性.許多原因致使學生無法充分認識到數形結合的重要性.

2.3 對數形結合的方法缺乏應用

雖然教師們都知道數形結合運用的重要性，但在具體教學中，卻缺乏靈活的應用.同時，部分數學教師對于數形結合的實際應用不夠了解，在具體教學中也不會用到該方法，且學生具備向師性，這就使教師的不了解成為學生的不了解，也無法了解到數形結合的重要性，這就使學生在解決數學問題的時候，不會應用數形結合，也不會通過數形結合促進學習效率的提高.

3 數形結合思想在初中數學解題中的應用策略

3.1 利用數軸促進絕對值問題解決

初中階段的數學教學中，教師在教學初始已引入了數軸，由于數軸和實數構建了一一對應關系，并為相反數、絕對值等全新概念等賦予了幾何意義.在對絕對值定義開展講解時，需對數軸知識進行學習，并引入實際問題.

例如，數軸上點A至原點之間的距離是3，點B至原點之間的距離是2，求A、B兩點之間的距離.

由數軸上來看，至原點的距離是3的點需分別置于原點的兩側且和原點之間的距離都是3個單位長度，因此，兩個點表示的數分別是+3與-3，也就是點A表示+3與-3，點B表示+2與-2，詳見圖1.此時，AB兩點之間的距離是1個單位長度或者是5個單位長度.

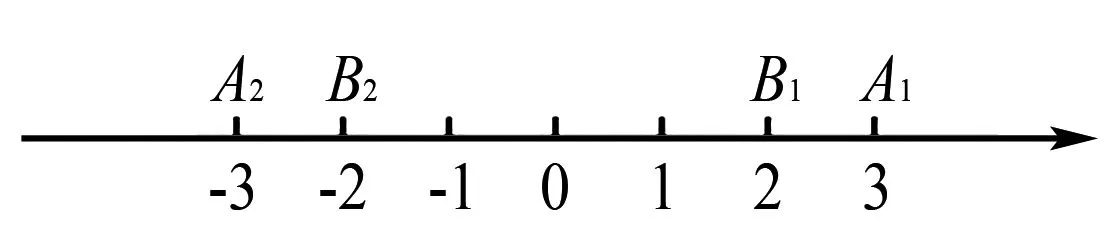
圖1

評析在本題中，絕對值的概念是能夠直接應用的，若不做圖，就會認為題目抽象，且容易丟一種情況，但將數值呈現于數軸上，不僅形象且直觀，而且還能促進數和形的有效融合，以深化學生對于知識的印象.

3.2 利用函數圖像促進方程、不等式問題解決

平面直角坐標系通常是在數軸后，又一個將代數和幾何有效銜接的工具，其擴大為有序實數對與平面中所有點都是一一對應的關系，將點轉變為線與面，更為初中時期重要的知識，即函數，提供了有效的生長土壤.而函數能夠與許多的知識有效結合，構成具有較強綜合性的數學題，如其能與不等式、方程等相聯系，通過函數圖像對不等式解的取值范圍、方程的根等進行解決.此時，教師可引導學生通過函數圖像對相關數學問題進行明了、直觀的解決，主要有以下形式.

3.2.1 函數與方程、方程組

一次函數y=kx+b(k≠0,k,b是常數)

①如果函數y=0的時候，會得出一元一次方程kx+b=0，這個時候，自變量x的值就是方程kx+b=0的解，其表示為圖像上則是一次函數圖像和x軸交點的橫坐標.

②如果x、y是兩個變量，因此，一次函數可看作為二元一次的方程kx-y+b=0.

③求取方程組的解通常就是求取兩個函數值相等的時候自變量的數值.二元一次方程組和一次函數的關系詳見圖2.

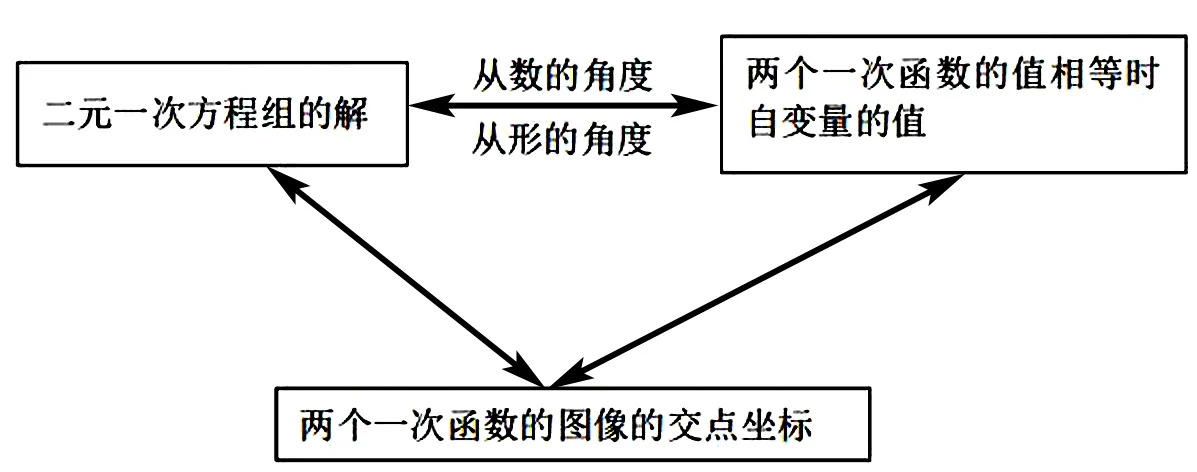
圖2

④二次函數y=ax2+bx+c(a、b、c為常數，a≠0)圖像和x軸的交點坐標是(x1,0)、(x2,0)，即x1、x2為方程ax2+bx+c=0的實數根，若y=ax2+bx+c的圖像和x軸無交點，那么，方程ax2+bx+c=0沒有實數根.二次函數y=ax2+bx+c(a、b、c為常數，a≠0)的具體圖像位于x軸上方的全部點的橫坐標的集合是一元二次不等式ax2+bx+c>0的全部解集，而圖像位于x軸下方全部點的橫坐標集合是一元二次不等式ax2+bx+c<0的全部解集.通過圖像進行方程解答，可通過二次函數y=ax2+bx+c(a、b、c為常數，a≠0)和一元二次方程ax2+bx+c=0之間的關系，進行圖形繪制，以做出解答.在對ax2=bx+c(a≠0)進行求解時，可將y=ax2和y=bx+c兩個圖像分別畫出，并找出兩個函數圖像的交點坐標.

3.2.2 函數和具體應用

具體的應用題一直屬于教師頭疼、學生害怕的題，但是，學習數學知識的主要目的就是進行實際問題的解決，也就是具體應用.因此，找出準確的方法，多加練習與總結極為重要.最為典型的就是通過平面幾何圖形，將問題圖形化，通過圖形進行問題的直觀解決，以促使問題的解答更加簡單、明了.

例如，某廠銷售一種面包，未銷售出去的可退回廠家，依據統計表明，單價為7角的時候，每天可售160個，售價每增加1角，每天少售20個，每個面包成本是5角，設面包單價是x角，每天銷售利潤是y角.

(1)通過x代數表示利潤與售賣個數的關系；

(2)求取y與x的函數關系式；

(3)面包單價為多少的時候，利潤最大？最大是多少？

分析二次函數主要反映了變量的數量關系與其變化規律的函數形式，基于此，在對具體問題和二次函數的問題進行研究時，可構建數學模型，通過二次函數具備的性質進行問題解決，通過數形結合，則能有效呈現該思想.

綜上所述，數形結合屬于極其重要的一種數學思想，在數學試題的解決中通常具有無法替代的作用，能夠將許多抽象化數學問題通過直觀形象的方式展現.因此，初中數學的解題教學中，需注重數形結合思想的運用，將復雜的數學問題簡易化，從而使學生的解題效率與準確率得以提高的同時，實現數學教學的整體質量提升.