從乘法分配律看七年級學(xué)生“去括號”與“合并同類項”的易錯點

鄧清 韋宏 廖怡寧

數(shù)學(xué)運算能力是一種通過熟練地掌握與運用算理和算法，準(zhǔn)確地得出運算結(jié)果的能力。《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2011版）》中明確指出，要重視對學(xué)生數(shù)學(xué)運算能力的培養(yǎng)。“去括號”和“合并同類項”是人教版七年級上冊“整式”一章的兩個重要內(nèi)容，它是初中生代數(shù)學(xué)習(xí)的基礎(chǔ)，也是數(shù)學(xué)運算能力培養(yǎng)的重要著力點。而在“去括號”和“合并同類項”的數(shù)學(xué)運算過程中，學(xué)生總?cè)菀壮霈F(xiàn)各種各樣的錯誤。戴再平認(rèn)為，學(xué)生解決問題的易錯源在于相關(guān)知識存儲不足或理解的偏差。因此，為了提高學(xué)生數(shù)學(xué)運算能力，夯實學(xué)生初中代數(shù)學(xué)習(xí)的基礎(chǔ)，教師需從運算的相關(guān)知識或理解出發(fā)，分析“去括號”和“合并同類項”錯誤產(chǎn)生的原因并找出錯誤的根源，及時糾正運算偏差。

“去括號”與“合并同類項”是七年級數(shù)學(xué)運算的重要內(nèi)容，學(xué)生在進(jìn)行運算操作時容易出現(xiàn)兩類問題：“去括號”的漏乘和符號錯誤、“合并同類項”中添括號的符號錯誤。本文通過辯證認(rèn)識乘法分配律與“去括號”“合并同類項”之間“源”與“流”的關(guān)系，分析算理根源之下學(xué)生易錯背后的認(rèn)知偏差，結(jié)合學(xué)生的情況提出從乘法分配律算理出發(fā)的整體處理問題的策略，幫助學(xué)生形成和深化對“去括號”與“合并同類項”的正確認(rèn)知，避免易錯、再錯。

整式的化簡是通過“去括號”和“合并同類項”來完成的，而“去括號”和“合并同類項”的實質(zhì)是乘法分配律在數(shù)式中的應(yīng)用。對于七年級學(xué)生而言，他們剛經(jīng)歷了數(shù)系的擴充，引入了負(fù)數(shù)，同時將原有的運算律在自然數(shù)集的應(yīng)用類比推廣到有理數(shù)集，這使得運算過程中需要重新審視“-”號的意義，不再單純以小學(xué)的減號來認(rèn)識，而是強化對負(fù)數(shù)的認(rèn)知。在學(xué)習(xí)整式時，學(xué)生初步接觸數(shù)系擴展之后的用字母表示數(shù)，這使得學(xué)生從小學(xué)單獨的數(shù)、用字母表示正數(shù)的概念認(rèn)知進(jìn)行了拓展，進(jìn)一步豐富了學(xué)生數(shù)與代數(shù)的認(rèn)知圖示，學(xué)生的抽象思維得到了更高層次的發(fā)展。但無論是負(fù)數(shù)引入帶來的“-”號的兩重含義，還是整式引入字母表示數(shù)等數(shù)學(xué)符號的增加，都是圍繞本質(zhì)內(nèi)容而呈現(xiàn)的外在表象和形式。運算中出現(xiàn)的眾多問題往往是由于學(xué)生局限于復(fù)雜外在的表象形式中，混淆了本質(zhì)內(nèi)容，形成了錯誤的理解。建構(gòu)主義理論強調(diào)學(xué)習(xí)者的主動性，在接觸新知識之前，學(xué)生在以前的學(xué)習(xí)生活中就有了一定程度的認(rèn)識，因此學(xué)生在接納新知識時并不是被動的，而是基于已有的水平和經(jīng)驗，主動選擇和加工信息，從而實現(xiàn)新舊知識的完全融合。而運算錯誤并不全是偶然，有些是存在規(guī)律的，這些有規(guī)律的錯誤是因為學(xué)生在新舊知識融合中構(gòu)建了自己獨有的概念。在此認(rèn)知下，學(xué)生要掌握“去括號”和“合并同類項”的運算，需要結(jié)合已有的知識經(jīng)驗，即乘法分配律在自然數(shù)集和有理數(shù)集中的應(yīng)用，撥開表象的重重迷霧，從本質(zhì)上認(rèn)識新知識，將易錯背后的觀念化為正確認(rèn)知。

一、知其源、悟之流

（一）乘法分配律之“源”

小學(xué)第一學(xué)段的主要內(nèi)容是自然數(shù)四則運算，而真正學(xué)習(xí)到基本運算律內(nèi)容是在第二學(xué)段。其實，運算律一直植根于自然數(shù)算法之中，在數(shù)的運算中不知不覺就有所運用。自然數(shù)集中的乘法分配律是從解決實際問題的過程中建模、抽象，概括得到概念及字母形式表達(dá)。但是，除了從實際生活中進(jìn)行建模，學(xué)生若能從更高觀點來認(rèn)識乘法分配律的來源，認(rèn)知便能達(dá)到更高層次。乘法分配律之“源”與數(shù)的發(fā)展密不可分。數(shù)的發(fā)展歷來有兩種源源不竭的動力：解決現(xiàn)實問題的需要（外在需要）和數(shù)系理論發(fā)展的需要（內(nèi)在需要），這兩種動力推動數(shù)的擴充。但是，數(shù)的發(fā)展中有一個恒定點，即保持運算律的有效性。也就是說，乘法分配律在數(shù)集的擴充中要保證有效性，這是“數(shù)與代數(shù)”的通性法則之一。在小學(xué)自然數(shù)集的乘法分配律中，滿足乘法對加法的分配律，而并不滿足乘法對減法的分配律，這是因為減法運算在自然數(shù)集中并不封閉。在七年級有理數(shù)中引入了負(fù)數(shù)，小學(xué)的減法和加法都可統(tǒng)一為有理數(shù)運算的加法。在引入新數(shù)、擴充數(shù)系的情況下，需要賦予乘法分配律在新數(shù)集以新定義，即有理數(shù)的乘法分配律。顯然，有理數(shù)的乘法分配律本質(zhì)上是與自然數(shù)的乘法分配律一致的，這即為乘法分配律之“源”。

（二）知“源”而看“流”

對于“去括號”運算，實質(zhì)上是根據(jù)乘法分配律順向展開。當(dāng)括號前為正數(shù)時，“去括號”的分配規(guī)則與自然數(shù)集中乘法分配律一致；當(dāng)括號前為負(fù)數(shù)時，則是將負(fù)數(shù)引入，變自然數(shù)集中的乘法運算為有理數(shù)集的乘法運算而形成的。比如，-9（a+b），此時由于有理數(shù)的乘法法則，這個式子經(jīng)由乘法分配律展開后即為-9a+（-9b）=-9a-9b，根據(jù)符號的變化，而概括歸納出“去括號”的規(guī)律，即為“去括號法則”。這是“去括號”于乘法分配律中的“流”。

1.錯解分析

例1錯解屬于“去括號”的漏乘，學(xué)生在對7（x+5）進(jìn)行去括號運算時，只把7分配給了x，而沒有分配給5，由此得到了7x+5；例2錯解屬于“去括號”的符號問題，學(xué)生未能掌握去括號后各項符號的變化規(guī)律，表現(xiàn)為只換了第二項，或者只換了第一項；例3為“去括號”的漏乘和符號問題的復(fù)合錯解情況。

在化簡整式的運算操作時，需要從算理根源——乘法分配律出發(fā)，靈活、準(zhǔn)確地展開操作。對于學(xué)生的去括號運算，常常出現(xiàn)漏乘及符號變化的“就近分配”：在“分配”的過程中，括號外的數(shù)通常只分配給首項，而其他項沒有；當(dāng)括號外的數(shù)為負(fù)數(shù)時，常常只對除首項之外的項分配而變號，或是對括號內(nèi)含“-”號的項改變符號。究其原因是學(xué)生在算術(shù)過渡到代數(shù)時對乘法分配律理解不夠透徹，認(rèn)知之中的分配并不是數(shù)與符號都乘以各項。從源頭來看，括號外的數(shù)與符號對括號內(nèi)各項的分配實質(zhì)上是統(tǒng)一的，都能歸結(jié)于乘法分配律。在引入負(fù)數(shù)之后，減法統(tǒng)一為有理數(shù)的加法，每一個多項式項與項之間是“+”的關(guān)系，而“-”號是這一項的負(fù)數(shù)屬性，與它自身相連。而在平時“去括號”的教學(xué)中，稍不注意，容易直接輸出給學(xué)生空洞的“去括號法則”的概念。學(xué)生的認(rèn)知并沒有建立起新舊知識之間的良好聯(lián)系，使得理解產(chǎn)生偏差，在操作中總是不能正確分配。

2.解決策略

（1）疏通根源，強化負(fù)數(shù)的整體認(rèn)知

根據(jù)建構(gòu)主義，學(xué)生是從已有經(jīng)驗與認(rèn)知出發(fā)，對新知識同化而構(gòu)建新的認(rèn)知。為了給予學(xué)生更好地過渡，糾正學(xué)生的錯誤理解，不妨從算理本質(zhì)引導(dǎo)和幫助學(xué)生深化對“去括號法則”的理解，整體看待符號與數(shù)，將其整體分配至每一項，在有理數(shù)的乘法運算下，得到正確的答案，矯正學(xué)生易錯。由此，可得：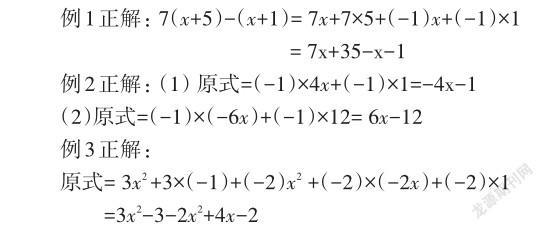

此時，符號的規(guī)律化為乘法分配律與有理數(shù)的負(fù)數(shù)乘法規(guī)則的結(jié)果，學(xué)生將晦澀生硬的“去括號法則”與已有的認(rèn)知構(gòu)建起了關(guān)聯(lián)，形成正確的理解。從理論源頭上充分認(rèn)識“去括號”的操作依據(jù)，在深層次的理論認(rèn)知基礎(chǔ)上，使得運算操作落地有根，運行有依，施展有方，有助于學(xué)生糾正易錯之下的理解偏差，達(dá)到對知識的通化理解。

（2）依據(jù)原理，分步落實

由此，依據(jù)乘法分配律形成“去括號”具體可行的操作步驟，引導(dǎo)學(xué)生依步驟操作，規(guī)范“去括號”的運算，此時，有助于基礎(chǔ)薄弱的學(xué)生進(jìn)行具體運算的操作和展開，形成嚴(yán)謹(jǐn)周密的思維。在操作練習(xí)之中，逐漸體會和領(lǐng)悟運算的原理，當(dāng)易錯背后的認(rèn)知突破和矯正之后，達(dá)到對運算本質(zhì)的理解，便可靈活進(jìn)行“去括號”運算。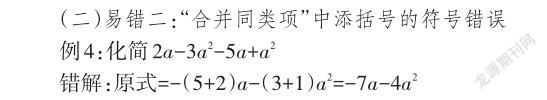

1.錯解分析

例4錯解屬于“合并同類項”中逆用乘法分配律進(jìn)行添括號時的符號問題。當(dāng)添括號之前為（-1）時，按照添括號法則（去括號法則的逆用）可知，括號內(nèi)各項要變號。但是學(xué)生往往也會因為只就近改變首項，沒有改變其他項而產(chǎn)生去括號的錯解。在平常教學(xué)中，教師易于單一地將此易錯歸因于學(xué)生記憶不深刻、粗心等，而并未究其更深層次的原因：學(xué)生對新知的理解并未在頭腦中與舊知形成較好連結(jié)，對添括號運算本質(zhì)的理解是模糊的。要幫助學(xué)生有效矯正對“合并同類項”易錯背后的理解偏差，首先要從乘法分配律出發(fā)，知道“合并同類項”的法理來源，從而判斷產(chǎn)生數(shù)學(xué)錯誤的現(xiàn)實背景；其次要根據(jù)法理來源尋找更能貼切學(xué)生認(rèn)知的解題思路，幫助學(xué)生一步步理解法理依據(jù)，從而進(jìn)一步強化正確概念。

2.解決策略：分析算理，厘清根源，合并運算

對于這道例題，學(xué)生在添括號時沒有對符號作相應(yīng)的變化，這說明在學(xué)生的理解中每一項并不包括“-”“+”，即沒有把符號、數(shù)字、字母整體看待。對此，不妨通過整體看待每一項來輔助學(xué)生對“合并同類項”的乘法分配律逆用的理解。

策略具體引導(dǎo)步驟：1.合并時添括號，括號與括號之間以加號連接；2.將同類項置于同一括號內(nèi)；3.進(jìn)行合并。注意：多項式的每一項已經(jīng)包括符號，故移動時需視之為整體，整體進(jìn)行加法交換律依據(jù)下的移動。

其實，“合并同類項”與“去括號”兩點易錯，實質(zhì)上都是乘法分配律的原因，悟其一，則通其二，兩者的易錯根源都應(yīng)從乘法分配律的來源分析和探求解決的策略，首先分步拆出可操作性的步驟，從理論和實踐方面給予學(xué)生充分的認(rèn)知梳理。其次，為學(xué)生提供充分的運算實踐的機會，在運算之中逐漸強化運算的步驟，體會“去括號”“合并同類項”的運算法理，逐漸糾正學(xué)生對易錯的思維認(rèn)知，提高學(xué)生運算的縝密性和養(yǎng)成依據(jù)原理和步驟自我監(jiān)控運算過程的學(xué)習(xí)習(xí)慣。由此，在每一次的運算操作學(xué)習(xí)以及練習(xí)中，逐步滲透給學(xué)生數(shù)學(xué)的法理和邏輯步驟規(guī)范性要求，將提高學(xué)生的數(shù)學(xué)運算能力的目標(biāo)分解細(xì)化，緩步趨近。

總而言之，“去括號”與“合并同類項”運算的易錯點需從“源流”即乘法分配律來分析，構(gòu)建對整式加減運算算理本質(zhì)的總體認(rèn)知，從算理根源即乘法分配律出發(fā)整體處理運算以矯正易錯。在教學(xué)中，講解整式運算問題的原理時，既要有一定的理論高度，又要通俗易懂，用學(xué)生能接受的語言、操作策略讓學(xué)生明白復(fù)雜的法理依據(jù)。而在解題實踐之中，需提煉出錯解背后深層次的原因，從“源流”予以分析、探尋對策，深化學(xué)生的理解，形成正確認(rèn)知，避免易錯、再錯。