基于K-LSTM-ecm模型的城市軌道交通短時客流預測

王金鋒，孫連英，張 天，涂 帥

（1.北京聯(lián)合大學 城市軌道交通與物流學院，北京 100101；2.北京聯(lián)合大學 智慧城市學院，北京 100101）

0 引言

我國正在經(jīng)歷世界歷史上規(guī)模最大、速度最快的城鎮(zhèn)化進程，隨之也帶來了新的問題，日益加劇的交通擁堵和環(huán)境污染困擾著人們。軌道交通作為準時、大運量的出行方式是解決城市交通問題的重要手段[1]。因城市軌道交通系統(tǒng)客流具有明顯的時效性，成為人們出行主要手段，也造成高峰時刻客流量過飽和的問題，影響城軌交通運營安全可靠性。如何采取有效的方式對客流量過大造成的隱患進行有預見性的運營規(guī)劃和安全防護，關鍵技術在客流預測[2]，通過挖掘客流特征實現(xiàn)城市軌道交通客流短時預測，可以為制定更加準確科學的運營方案以及提高運營服務水平提供有效的解決途徑。

應用于城市軌道交通客流預測的模型主要包括計量模型以及人工智能模型。常見的計量模型如：卡爾曼濾波（Kalman）模型[3]、自回歸滑動平均模型（Autoregressive Moving Average Model，ARMA）[4]。回歸模型對于刻畫中長期客流的變化趨勢有良好的效果，然而對數(shù)據(jù)中出現(xiàn)的隨機變化敏感度不足，難以精準進行隨機性較高的短時客流預測。而應用支持向量回歸模型（Support Vector Regression，SVR）[5]、神經(jīng)網(wǎng)絡（Back Propagation，BP）[6]等人工智能模型對客流數(shù)據(jù)擬合程度更高，通過自身學習能力以及自適應能力可以更好捕捉非線性規(guī)律從而提升預測精度，但對描述輸入與輸出之間聯(lián)系的能力有限，參數(shù)的訓練過程也相對較慢。其中，中長短期記憶網(wǎng)絡（Long Short-Term Memory，LSTM）[7]在處理時序性數(shù)據(jù)的時間特征時有很好的效果，能夠處理長間隔跨度數(shù)據(jù)有效信息消失的問題。但單一使用LSTM進行短時客流預測仍存在一定的局限性。因此，本文構建了K-means聚類、LSTM以及誤差修正模型（ErrorCorrection Model，ecm）結合的K-LSTM-ecm的城市軌道交通短時客流預測模型。

1 K-LSTM-ecm模型構造

1.1 K-LSTM-ecm模型

本文以LSTM模型作為主模型，在此基礎上增加K-means聚類以及誤差模型構建城市軌道交通短時客流預測模型。LSTM模型首次發(fā)表于1997年，其獨特的設計結構適用于處理時間序列性數(shù)據(jù)，對預測時間序列中的長間隔和延遲有很好的處理效果，LSTM模型在預測問題上的表現(xiàn)優(yōu)于時間遞歸神經(jīng)網(wǎng)絡（RNN）以及馬爾科夫模型（HMM）。作為非線性模型，LSTM模型適用于預測客流數(shù)據(jù)這種非線性數(shù)據(jù)[8]。本文提出的K-LSTM-ecm模型通過以下流程實現(xiàn)城市軌道交通短時客流預測。

1）基于客流數(shù)據(jù)的短時間隨機性、長期周期性以及同類型臨近站點的空間客流分布，構建前d天q個歷史客流數(shù)據(jù)的數(shù)據(jù)集合，利用LSTM模型對時序性數(shù)據(jù)的敏感性，對預測目標站點及其同類型相鄰站點的時間、空間關系進行提取。

2）探究預測目標站點及其同區(qū)域相鄰站點工作日、非工作日（節(jié)假日、周末）客流特點，以單個時段客流數(shù)據(jù)作為樣本點，采用K-means算法進行聚類分析生成聚類標簽，將最終聚類后的數(shù)據(jù)作為主模型的輸入數(shù)據(jù)。

3）將第一次LSTM模型輸出的y-pre作為ecm模型輸入，對y-pre進行協(xié)整分析，以發(fā)掘第一次預測值與真實值之間的協(xié)整關系，并構成誤差修正項建立ecm模型。將誤差反饋到LSTM模型，最終實現(xiàn)城市軌道交通短時客流預測。K-LSTM-ecm模型框架如圖1所示。

圖1 K-LSTM-ecm模型框架

1.2 輸入數(shù)據(jù)構造

城市軌道交通在網(wǎng)絡化運營條件下，不同區(qū)域站點有不同的客流特點，可分為居住密集型、崗位密集型、混合型和樞紐型4類[9]，同類型臨近站點之間的客流分布相互影響。城市軌道交通網(wǎng)絡化運營導致了客流不僅受本站歷史時段客流量的影響，還會受相鄰站點客流分布的影響，因此構建輸入數(shù)據(jù)時不僅要考慮預測目標站點的歷史客流數(shù)據(jù)時間特征，還要考慮同類型區(qū)域相鄰站點客流的空間分布特征，以達到更好描述目標站點客流特點的效果，從而提升預測精度。

將目標站點定位為N（1＜N，n=1，2，3，…，N），用XNT，t表示目標站點T天第t時刻的客流量，由于同類型臨近站點客流特點具有相似性，輸入數(shù)據(jù)按空間位置關系將相關站點表示為XN-nT，t。對于N站點的T天第t時段的客流預測來講，由于客流具有連續(xù)性，輸入的客流數(shù)據(jù)應考慮其前q個時段的客流量以及前d天的連續(xù)性客流量，故模型輸入數(shù)據(jù)集如式(1)表示：

1.3 工作日與非工作日聚類分析

城市軌道交通作為市民的出行首選交通方式，其客流分布與市民的出行模式相關，不同車站所處位置在一定程度上能反映其客流規(guī)律，如：在居住密集型區(qū)域地鐵站，受乘客們的出行目的影響，工作日與非工作日（節(jié)假日、周末）的客流時段分布差異較大。工作日期間，絕大多數(shù)乘客都是通勤乘客。客流潮汐式分布十分明顯，表現(xiàn)在高峰時期客流量巨大，早高峰時段進站乘客數(shù)量遠多于出站乘客數(shù)量，晚高峰與之相反。客流在工作日期間分布具有顯著的突峰特征，早高峰客流出現(xiàn)峰值。

非工作日期間，乘客出行目的區(qū)別于工作日，會出現(xiàn)一定商務客流、出行客流等，因而客流分布與工作日有所區(qū)別。節(jié)假日和周末客流無工作日的潮汐式分布，全天各時段進站乘客數(shù)量較為均衡，無明顯低谷，一般呈全峰型分布。同時，節(jié)假日和周末的客流分布具有相似性。

為進一步量化工作日和非工作日單日客流量之間的相似性，本文選取Pearson相關系數(shù)對于客流數(shù)據(jù)進行相關性分析，其能夠精準地表達數(shù)據(jù)之間的數(shù)量關系，從而達到定量分析和比較。結果如表1所示。

表1 工作日和周末客流相關性分析

圖2 工作日進站客流分布

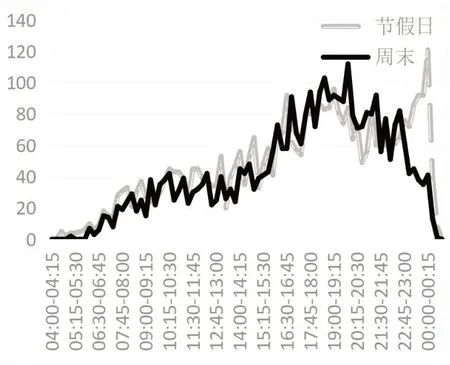
圖3 節(jié)假日與周末進站客流分布對比

表2 周末和節(jié)假日客流相關性分析

由上表，周一至周五單日客流之間均呈強相關性，周六和周日客流數(shù)據(jù)之間同樣呈強相關性，而工作日數(shù)據(jù)和周末數(shù)據(jù)呈中相關性，究其原因，周末的客流組成區(qū)別于工作日的客流，客流隨機性更強，故導致該結果；周末和節(jié)假日數(shù)據(jù)之間呈強相關性，但其系數(shù)表現(xiàn)上與其他強相關數(shù)據(jù)比略低。

通過上述相關性分析結論，工作日期間單日客流量相似性極強，非工作日同工作日一樣，為進一步提升短時客流預測精度，本文采用K-means聚類算法對客流數(shù)據(jù)進行聚類并生成聚類標簽。K-means聚類的無監(jiān)督分類方法可以無監(jiān)督地探索客流數(shù)據(jù)的內(nèi)部結構特征，將具有較強相似性的數(shù)據(jù)劃分為相似的數(shù)據(jù)集。因此，本文采用K-means聚類算法將采集到的客流數(shù)據(jù)劃分為工作日和節(jié)假日聚類集，不同類別間數(shù)據(jù)相似度越小越好。相似的通過樣本之間的距離表示，兩個樣本之間距離越小，說明樣本之間相似度越高，反之，說明相似度越小。對于樣本之間距離的計算通常通過歐式距離計算二維空間，高維度空間多采用馬氏距離和曼哈頓距離等。歐式距離計算公式如下：

K-means聚類算法基本計算思想：

首先對有n個數(shù)據(jù)點的數(shù)據(jù)集從n個數(shù)據(jù)點中隨機選取k個點作為初始聚類中心，再通過歐氏距離計算對靠近各聚類中心的數(shù)據(jù)進行分類，采用迭代的方式，在上述過程中不斷更新聚類中心點，直至整體達到穩(wěn)定的狀態(tài)，獲得聚類中心C。

K-means聚類算法計算基本步驟：

1）輸入一個數(shù)據(jù)集，確定聚類中心數(shù)目k；

2）在數(shù)據(jù)集中隨意生成k個初始聚類中心；

3）計算聚類中心點與其他數(shù)據(jù)點的距離，取距離最小值；

4）計算同一聚類中所有對象的均值并加以統(tǒng)計，將計算結果更新替換為新的聚類中心；

5）重復上述步驟，直至結果穩(wěn)定，聚類中心不再變化，輸出。

1.4 LSTM模型

LSTM模型在RNN結構基礎上，添加了各層的閥門節(jié)點。LSTM結構如圖4所示，其結構由遺忘閥門（forget gate），輸入閥門（input gate）、輸出閥門（output gate）以及細胞狀態(tài)組成。

圖4 LSTM神經(jīng)元結構

這些閥門可以打開或關閉，用于判斷模型網(wǎng)絡的記憶態(tài)（之前網(wǎng)絡的狀態(tài)）在該層輸出的結果是否達到閾值，從而加入到當前該層的計算中，閥門節(jié)點利用Sigmoid函數(shù)將網(wǎng)絡的記憶態(tài)作為輸入計算；如果輸出結果達到閾值則將該閥門輸出與當前層的的計算結果相乘作為下一層的輸入；如果沒有達到閾值則將該輸出結果遺忘掉。每一層包括閥門節(jié)點的權重都會在每一次模型反向傳播訓練過程中更新。具體計算過程如式(3)～式(8)所示：

其中，W表示輸入向量與輸入閥門、輸出閥門等之間相對性的權向量，b為偏置變量。

1.5 ecm模型

誤差修正模型（ecm）是1978年由Davidson等提出的表示變量之間的一種長期均衡關系的模型，這種均衡關系可能會在短期內(nèi)出現(xiàn)波動或者偏離這種均衡關系[10]。該模型通過對誤差的修正，可以使變量重返均衡狀態(tài)。不僅考慮到了短期波動，還兼顧長期趨勢影響，對于城市軌道交通客流預測模型有良好的修正效果，其表達式如式(9)所示。

其中，λ1、λ2為各變量差分項的系數(shù)，反映了模型短期的動態(tài)變化；φ為修正系數(shù)，也稱調整速度，通常為負值；ecmt-1為誤差修正項；c為模型的常數(shù)項。

2 案例分析或實證分析

2.1 實證數(shù)據(jù)

本文以北京地鐵回龍觀站為預測目標站點，該站位于北京市大型社區(qū)回龍觀地區(qū)的核心位置，是典型的居住密集型區(qū)域地鐵站，日常客流潮汐現(xiàn)象明顯且客流量巨大，并呈現(xiàn)非線性特征。本文選取北京地鐵AFC客流數(shù)據(jù)作為K-LSTM-ecm模型的輸入數(shù)據(jù)集。選取4：00到第二日00：30作為預測時段，進行數(shù)據(jù)預處理，除去重復值與異常值。選取15min為一個間隔，每日84個統(tǒng)計時段，以便于指導站點實際運營管理以及緊急情況預警。

3.5 金屬蛋白酶結構域10(ADAM10) 去整合素和ADAM10是APP剪切的主要α分泌酶，能阻止Aβ產(chǎn)生[27]。ADAM10過表達能預防淀粉樣病變和提高長時程增強作用及學習記憶功能[28]。ADAM10中罕見的編碼變體與晚發(fā)家族AD相關。沒有關于ADAM10與自噬和AD相關的報道，但最近一則報道指出在內(nèi)皮細胞中ADAM10可以被自噬調節(jié)，反過來調節(jié)小鼠對內(nèi)皮ADAM10相關疾病狀態(tài)的敏感性[29]。因此，有可能ADAM10在神經(jīng)元和神經(jīng)膠質細胞也可以被自噬調節(jié)。神經(jīng)元和膠質細胞ADAM10的自噬調節(jié)及AD相關的ADAM10變體對自噬的影響需要在將來的研究中得到闡明。

依據(jù)地鐵站所處區(qū)域屬性相同，客流分布相似的特點，選取同區(qū)域鄰近地鐵站霍營站和龍澤站。為直觀地分析所選三個站點的客流分布規(guī)律，隨機選取一天三個站點的進站客流進行對比，如圖5所示。

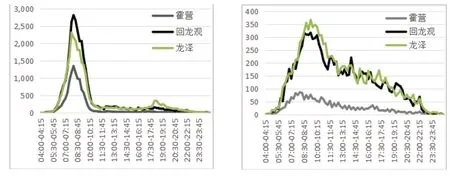
圖5 同類型區(qū)域站點全天客流對邊圖（節(jié)假日、工作日）

可以看出，所選三個同區(qū)域相鄰站點工作日出站客流分布曲線整體相似性強，由于回龍觀站所處于居住密集型區(qū)域，主要客流為通勤客流，進站客流量分布呈現(xiàn)早高峰時段（8∶00-10∶00）客流激增的情況，而晚高峰時段（5∶00-21∶00）并未出現(xiàn)客流激增的特點，客流峰值出現(xiàn)在8∶30-8∶45時段；節(jié)假日客流相比工作日客流分布較為均衡，在19∶00-19∶15時段三站出站客流均呈平緩上升趨勢。故選取地鐵龍澤站、回龍觀站以及霍營站的客流數(shù)據(jù)為模型輸入數(shù)據(jù)集。

2.2 時段選擇選擇

預測規(guī)定站點的客流量受前q個相鄰時段客流數(shù)據(jù)影響，不同q值會影響預測精度，為確認合理q值，本文根據(jù)地鐵站客流分布規(guī)律、客流的周期性以及每日運營時段數(shù)設計實驗，分別選擇q=5、10、15、20，以回龍觀站歷史客流數(shù)據(jù)為訓練數(shù)據(jù)集，最大訓練迭代次數(shù)為10進行試驗，以標準差（RMSE）作為判斷依據(jù)。q值取5、10、15、20時模型標準差如表3所示。

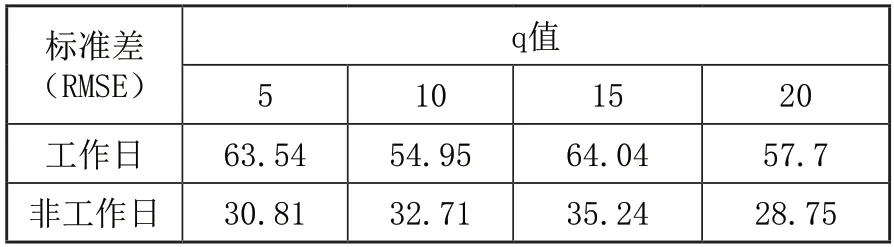
表3 q取不同值的標準差

由實驗得出結論，當q值取10時，標準差最小，因此工作日預測結果較為精準。也就說明對預測當前時段客流量，前5個時段客流量與預測時段客流量聯(lián)系緊密；而非工作日的客流分布波動相對平緩，標準差值相差不大，其中q值取20時標準差最小。在后續(xù)實驗中設定工作日q值取10，非工作日q值取20進行模型性能實驗。

2.3 實驗模型訓練流程

本節(jié)以地鐵回龍觀站進站客流為例進行預測，構建K-LSTM-ecm城市軌道交通短時客流預測模型進行實驗，其實驗參數(shù)設置為包含一個輸出層、兩個隱含層和一個輸出層，輸入層神經(jīng)元個數(shù)為5，隱含層的節(jié)點數(shù)為（100，100）輸出層神經(jīng)元個數(shù)為1。工作日q值取10，非工作日q值取20。

K-LSTM-ecm模型訓練流程如下：

1）將三個站點客流數(shù)據(jù)進行K-means聚類并生成標簽；

2）將聚類后的客流數(shù)據(jù)劃分為訓練集和測試集；

3）將LSTM神經(jīng)網(wǎng)絡模型網(wǎng)絡權重及其參數(shù)進行初始化處理；

4）選取ReLU函數(shù)為激活函數(shù)，并向前傳播輸出單個神經(jīng)元輸出值；

5）選取平方損失函數(shù)為損失函數(shù)，并向后傳播誤差值；

6）計算梯度；

7）采用Adam函數(shù)為優(yōu)化函數(shù)，更新參數(shù)；

8）輸出預測結果到ecm誤差補償模型，計算誤差，輸出誤差到LSTM神經(jīng)網(wǎng)絡；

9）輸出預測結果。模型訓練流程如圖6所示。

圖6 K-LSTM-ecm模型訓練流程

為了后續(xù)實驗的公平性及準確性，對照模型K-LSTM模型與LSTM模型的參數(shù)取值與K-LSTM-ecm模型一致。

2.4 模型性能分析

本文選取北京地鐵龍澤站、回龍觀站以及霍營站歷史客流數(shù)據(jù)集驗證K-LSTM-ecm模型效果，數(shù)據(jù)集為2020年9月1日至10月8日全天出站客流數(shù)據(jù)，數(shù)據(jù)總量為9577條，其中每條數(shù)據(jù)包含4個輸入數(shù)據(jù)，主模型輸入數(shù)據(jù)為同一天預測時段前q個時段客流數(shù)據(jù)、同類型站點同時段客流數(shù)據(jù)、日期數(shù)據(jù)以及工作日、節(jié)假日聚類標簽數(shù)據(jù)，輸出數(shù)據(jù)為當前時段的預測客流數(shù)據(jù)。為保證模型穩(wěn)定性，提升預測精度以及模型訓練速度，將輸入數(shù)據(jù)歸一化處理。劃分2020年9月23日至10月8日為測試集，其余為訓練集。使用python語言進行建模。為驗證模型選取LSTM模型、K-LSTM模型進行對比。預測結果如圖7、圖8所示。

圖7 工作日預測結果

圖8 節(jié)假日預測結果

由預測結果顯示以及進站客流的結果圖可知，客流受時間因素較大，進站客流同真實客流一樣呈現(xiàn)集中現(xiàn)象，主要集中在早高峰數(shù)段7：00-9：30。對于非工作日真實客流所展現(xiàn)的客流波動性，LSTM模型波動時段與真實客流不符，K-LSTM模型客流波動范圍相較K-LSTMecm模型與真實客流有所差異。故客流除LSTM短時客流預測模型效果不理想，K-LSTM模型與K-LSTM-ecm模型都對未來客流進行有效預測。但對客流隨機性波動K-LSTM-ecm模型直觀上看效果更優(yōu)，與真實客流量曲線趨勢更加貼近。為更精準對比預測結果，本文選取RMSE、MAE、MAPE作為模型評價指標，以驗證模型有效性，結果如表4所示。

表4 模型評價指標

由上表數(shù)據(jù)可知，本文構建的K-LSTM-ecm模型在三個評價指標表現(xiàn)上均優(yōu)于單一的LSTM模型與未采取誤差補償模型的K-LSTM模型。

3 結語

對于城市軌道交通的客流預測，現(xiàn)有研究對于歷史客流數(shù)據(jù)的時間特征有很多理論成就，而對于空間特征多是考慮整體地鐵路網(wǎng)的空間關系，為更加細化空間特征，本文根據(jù)地鐵站同類型相鄰原則構建考慮時空特征的K-LSTM-ecm模型，進一步提升預測精準度。為更精準預測客流，本文設計實驗，選取q個臨近歷史客流量，結果表明：預測當前時段的客流時，工作日前10個時段客流數(shù)據(jù)影響最大，而節(jié)假日則受20個時段客流影響。為進一步證明K-LSTM-ecm模型效果，設計對比實驗，將模型與LSTM模型與K-LSTM模型進行直觀的折線圖結果比較與評價指標比較，研究表明，在進行K-means聚類生成聚類標簽，實現(xiàn)了對歷史客流數(shù)據(jù)集客流特征的細化，更加有效的描述了客流特征且提高了預測精度。實驗結果顯示K-LSTM-ecm模型優(yōu)于LSTM模型與K-LSTM模型，進而驗證了模型的有效性。