基于均衡準則的多目標即時配送路徑優化模型
□ 于江霞 卞 喆 羅太波
(西安電子科技大學 經濟與管理學院, 陜西 西安 710126)
[基金項目]教育部人文社會科學基金項目(20YJAZH123,18YJC630114);陜西省自然科學基金項目(2020JM-211);國家自然科學基金項目(72101196,71701162)。
一、引 言
隨著近場電商的發展及消費體驗升級,在線外賣市場規模持續增加,2019年中國餐飲外賣產業規模達到6 536億元,相比2018年增長了39.3%[1]。面對持續增長的訂單量和愈發激烈的行業競爭,外賣平臺更加關注配送時效和成本,卻忽略了派單機制的合理性及騎手的權益,導致派單不均衡,騎手收入差距過大,配送員心理失衡引起矛盾激化,頻發“騎手抗議強制派單”事件[2]。不合理的派單模式已成為影響即時配送行業持續健康發展的重要因素,是即時配送平臺亟需解決的現實問題。平臺任務分派實質取決于配送路徑的優化,因此本文在均衡準則下兼顧配送成本和客戶滿意度,研究在不大幅增加成本和降低客戶滿意度的前提下,均衡配送員派單量、提高工作量與收入適配度的方案,進一步穩定配送隊伍,促進外賣行業健康發展。
即時配送具有取送貨、商家和客戶有序配對的特征,有嚴格的先后訪問順序,且對配送準時性要求較高,因此該類問題可歸結為同時取送貨的車輛路徑問題(vehicle routing problem with simultaneous pickup and delivery,VRPSPD)。針對VRPSPD問題,學者們在不同約束條件下對配送成本或客戶滿意度進行了優化研究[3-7]。然而追求單一目標的優化方案易忽略其他限制,不能達到實際最優。因此,學者們開始考慮多方面的綜合優化,如考慮最小化車輛數及總行駛成本[8],最小化運輸成本和最大化客戶滿意度[9],最小化車輛路徑總長度、最小化客戶等待總時間[10],車輛行駛總里程最小和服務準時率最大[11],運輸成本和路徑最大長度差最小[12],考慮顧客層級的固定成本、運輸成本和超時懲罰成本最小[13]等。近年來,部分學者開始考慮工作量均衡對車輛路徑問題進行探討,如Rabbani等[14]考慮工作量均衡和時間窗約束對危險廢物的配送路徑問題進行研究,孫麗君等[15]考慮司機工作量均衡對成品油配送方案進行優化。
可見,配送路徑優化問題已引起廣泛關注,但多集中于配送成本和客戶滿意度的優化,訂單分配不均、工作量負荷過重、群體內收入與工作量不匹配等問題較少涉及。本文兼顧平臺、客戶和配送員三方利益,對配送成本、客戶滿意度和均衡配送員收入三個目標進行綜合優化,不僅能夠提高配送員訂單任務的均衡性,緩解收入不均、訂單量負荷過重的矛盾,也從一定程度上有助于解決員工高離職率問題,對即時配送行業的有序健康發展具有重要的現實意義。
二、問題描述及模型構建
(一)問題描述
某平臺在一段時間內接到N個訂單,對商家和客戶提供一對一的取送服務。配送員從初始位置出發,配送完成后無需返回。需要合理安排配送路線,實現均衡配送員收入、最小化配送成本和最大化客戶滿意度的綜合優化。不失一般性,做如下假設:
(1) 配送員須先到商家取貨再配送至客戶點,訪問順序不能顛倒;
(2) 商家和客戶能且僅能被服務一次;
(3) 不考慮配送車輛的容量約束;
(4) 配送車輛具有最大行駛里程約束;
(5) 配送車輛行駛速度恒定;
(6) 送貨時的時間損耗忽略不計;
(7) 客戶滿意度僅與物品送達時間有關。
(二)參數及變量分析
集合和變量定義,見表1。
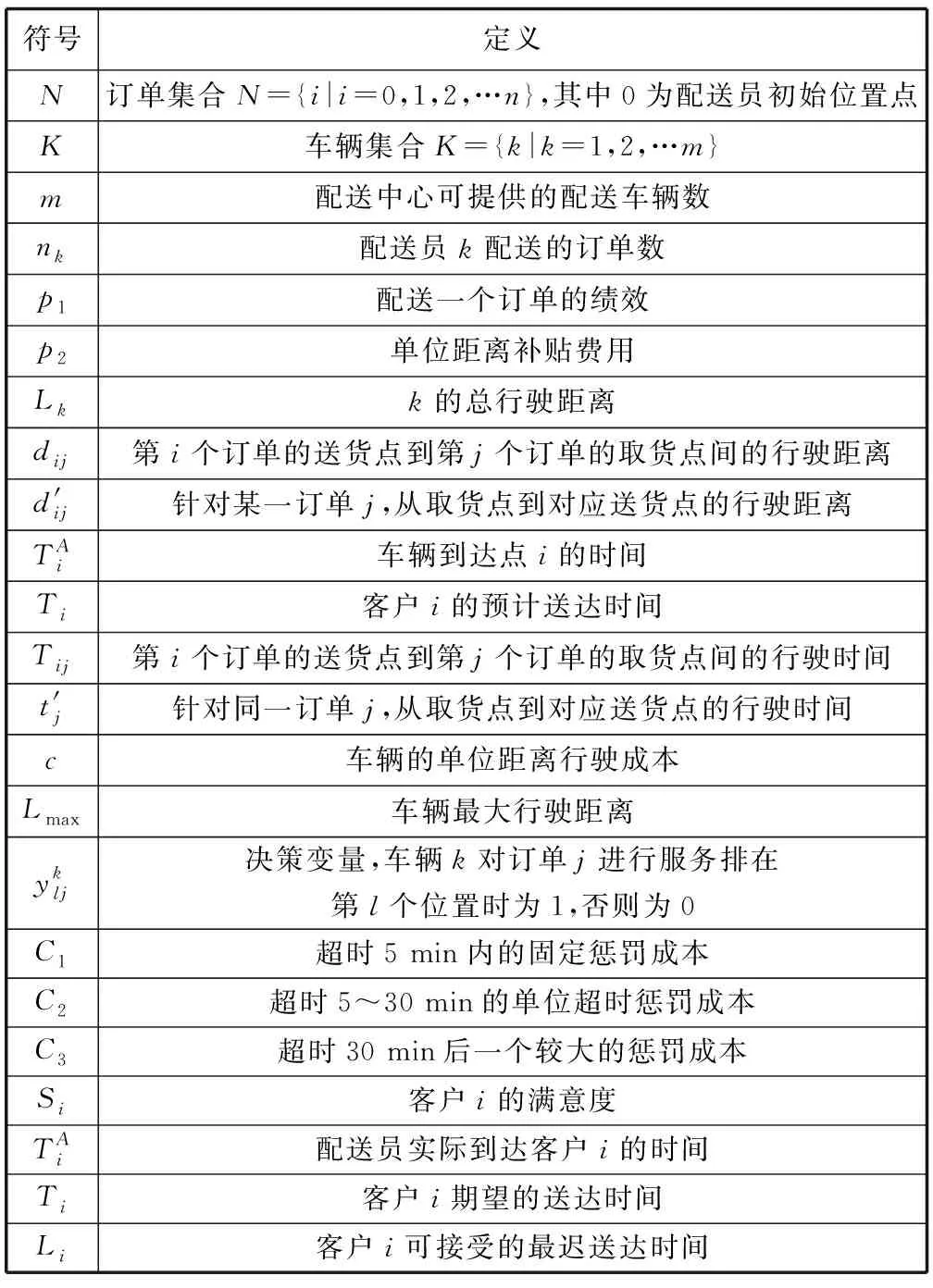
表1 集合和變量定義
(三)配送員績效工資
根據即時配送工資構成[16],配送員績效主要包含訂單量和行駛距離,配送距離超過兩公里后有距離補貼,因此配送員k的績效工資可表示為:
Fk=nk×p1+max(Lk-2,0)×p2
(1)
(四)訂單超時懲罰成本
即時配送平臺有嚴苛的超時懲罰措施,一旦配送超時,則扣除一半配送費;若客戶給予差評,則直接扣除50~100元的罰款。根據《2016年餐飲消費調查報告》,有12%的消費者不習慣等待,超半數的消費者可以接受15分鐘以內的等待時間,接近30%的消費者可以接受15~30分鐘的等待,愿意接受半小時以上等待時間的僅占7%[17],顧客對不同超時時長容忍度不同[18]。本文引入容忍度概念,結合顧客可容忍的超時時間范圍,設置分段超時懲罰成本函數 ,如圖(1)和式(2)所示。
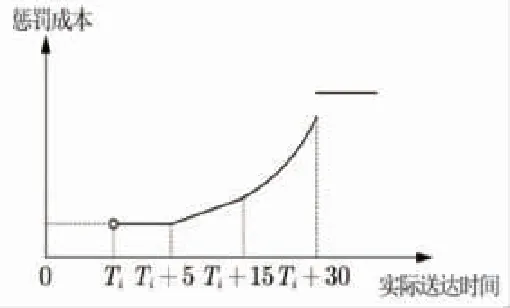
圖1 懲罰成本函數
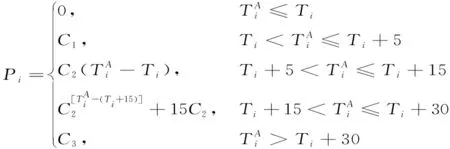
(2)
(五)客戶滿意度函數
經過對美團外賣平臺客戶評論信息進行統計分析,發現客戶滿意度主要取決于送達時間,客戶大多偏好于在預計送達時間前得到服務,晚于該時間點則滿意度下降,且超時越長滿意度越低。因此,本文以配送準時性作為衡量客戶滿意度的指標,配送超時客戶滿意度呈線性下降,滿意度函數如圖(2)和式(3)所示。
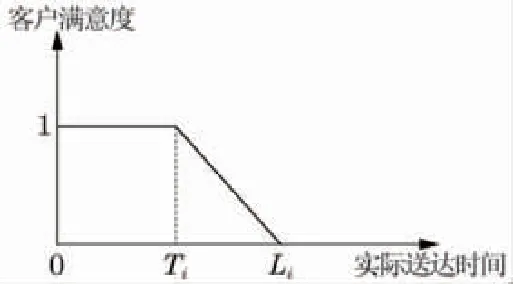
圖2 時間滿意度函數
(3)
實際配送中輕微超時不可避免。統計發現客戶給予投訴或差評,98%是由于極端超時造成的。因此,為減少極端超時情況的發生,本文以最小化客戶最大不滿意度為目標,則客戶不滿意度函數為S′i=1-Si。
(六)模型建立
構建最小化配送員工資極差、最小化配送成本和最小化客戶最大不滿意度的多目標優化模型:
(4)
(5)
min maxS′i,i∈N
(6)
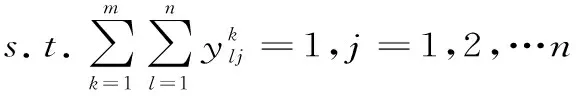
(7)
(8)
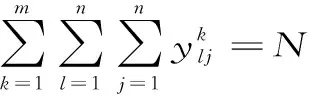
(9)
(10)
l=1,2,…n,k=1,2,…m
(11)
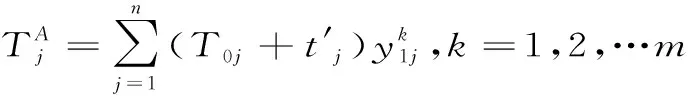
(12)
i,l=1,2,…n,k=1,2,…m
(13)
式(4)表示最小化配送員薪酬極差;式(5)表示配送總成本最小;式(6)表示最小化客戶最大不滿意度;式(7)和式(8)確保每個訂單僅能被一輛車服務一次;式(9)表示每個客戶都得到配送服務;式(10)確保任一輛車的配送訂單順序相連,防止出現空單行駛現象;式(11)為配送車輛的行駛里程約束;式(12)與式(13)為訂單的到達時間限制。
(七)多目標問題的處理
將min maxS′i轉化為Z3=minb1及k個約束條件:f1(x)≤b1,f2(x)≤b1…fk(x)≤b1其中:
fk(x)=S′i
(14)
式(4)、(5)和(6)的隸屬度函數可以定義為具有同一量綱的單目標函數式:

(15)
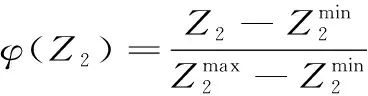
(16)
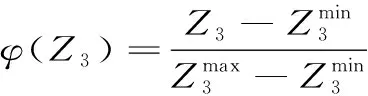
(17)
由于各目標重要度不同,采用自適應權重法來確定各目標的權重值ω1,ω2和ω3,則統一量綱后的單目標函數模型為:
minZ=ω1φ(Z1)+ω2φ(Z2)+ω3φ(Z3)
(18)
該問題屬于NP-hard問題,若采用精確算法易產生指數爆炸,難以在規定時間內求得模型最優解,而蟻群算法因其具有正反饋機制、較強的適應性和尋求最優解的能力等優勢在路徑優化問題中廣泛應用,適用于求解此類問題。
三、混合蟻群算法設計
考慮即時配送具有取送貨、商家和客戶有序配對的特征,將遺傳算法和蟻群算法相結合設計混合蟻群算法,在標準蟻群算法中加入遺傳算法的交叉和變異操作,迭代更新路徑上的螞蟻狀態,通過自適應增量系數和揮發系數對信息素進行優化。算法框架如圖3所示。具體算法步驟如下:
步驟1:參數初始化。設定信息素因子α、啟發信息因子β、信息素揮發系數ρ、最優個體數目e。
步驟2:設定當前迭代次數t=0,最大迭代次數T;當前蟻群規模n=0,最大蟻群規模N;當前行動螞蟻k=0,螞蟻數量K。
步驟3:初始化一隊蟻群,并初始化每個螞蟻的禁忌表,可訪問客戶節點表和共同可訪問的商家節點表。
步驟4:所有訂單配送完成判斷,判斷每個螞蟻的可訪問客戶節點和共同可訪問商家節點是否都為空,若都為空則進入步驟9,反之進入步驟6。
步驟5:配送員k是否配送完成判斷,判斷螞蟻k的可訪問客戶節點和共同可訪問商家節點是否都為空,若都為空則進入步驟8,反之進入步驟7。
步驟6:按概率確定螞蟻移動到下一個節點的位置。在螞蟻k的可訪問客戶節點或共同可訪問商家節點中選擇一點加入禁忌表,若是商家節點則需要把對應的客戶節點加入螞蟻k的可訪問客戶節點。
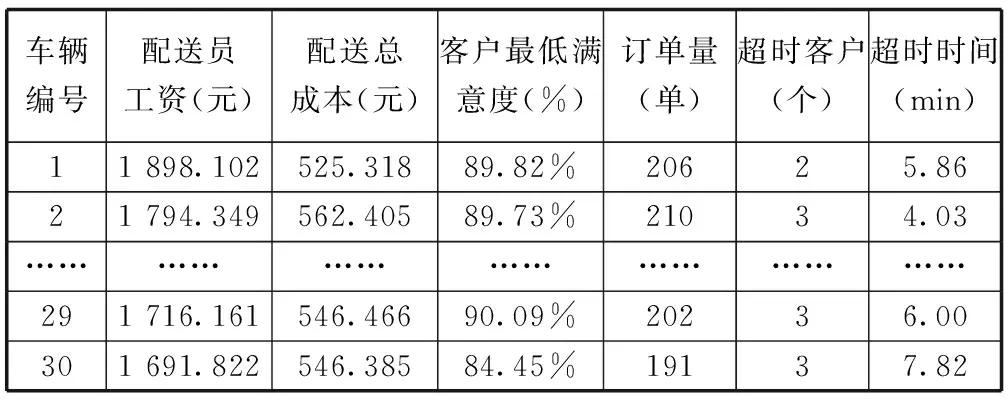
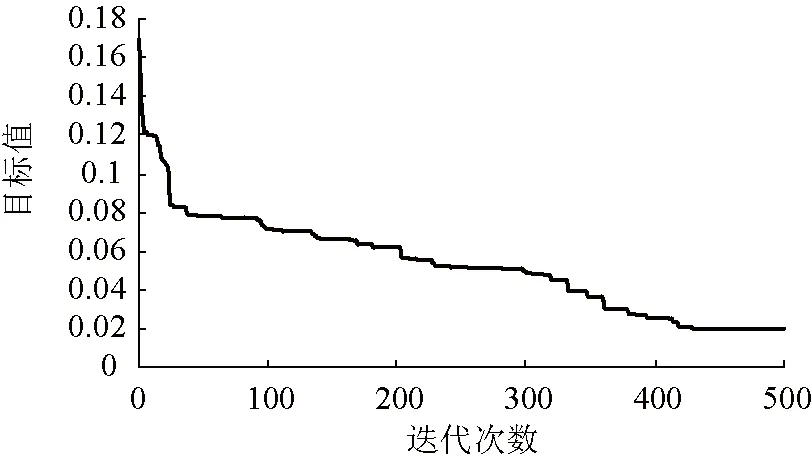
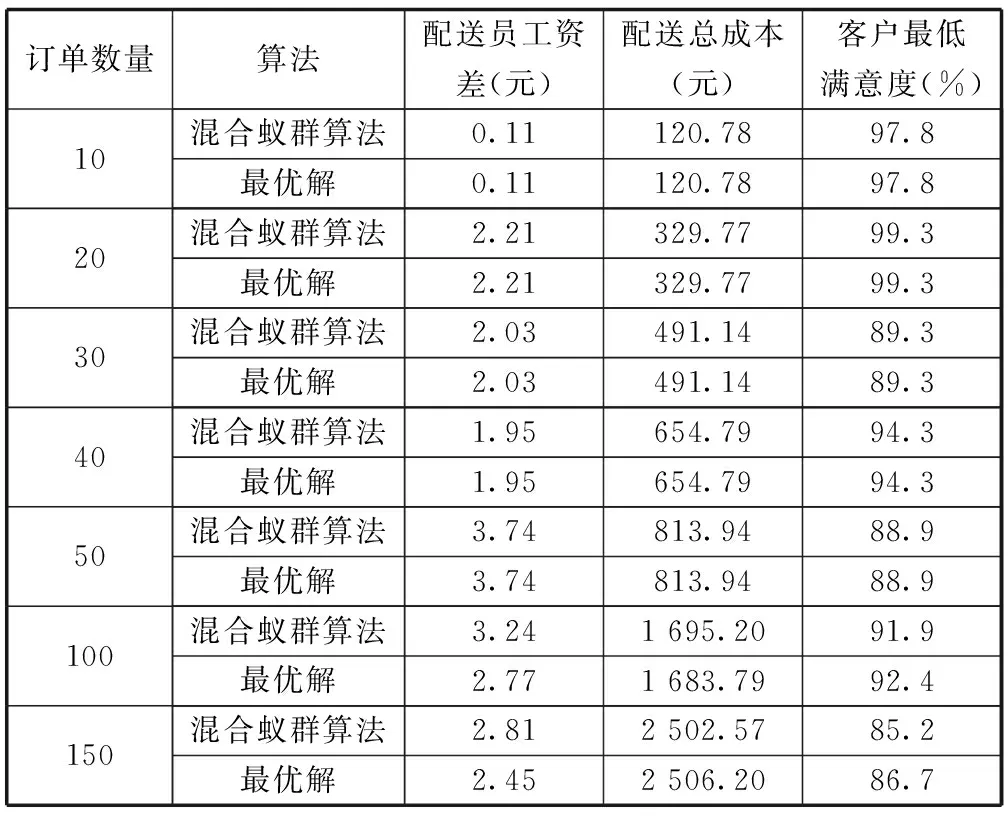
步驟7:令k=k+1,若k 步驟8:令n=n+1,若n 步驟9:混合蟻群算法的交叉操作。以某一父代中配送員的順序為基準,對另一父代中的螞蟻進行排序,之后將每個配送員的禁忌表根據配送員的順序進行拼接,以生成兩條父代染色體。在兩條父代染色體中隨機確定一對交叉點,進行交叉操作生成子代,然后解碼成禁忌表。 步驟10:混合蟻群算法的變異操作。確定父代染色體k個配送員的禁忌表進行變異操作,首先按概率選擇變異點、并找到相應的配對點,隨機確定商家、客戶節點需要變異的位置,剩余基因原序填充至空余基因位,以生成一條子代染色體。 圖3 混合蟻群算法流程圖 步驟11:根據自適應權重系數處理多目標優化問題。將多個目標建立為具有同一量綱的單目標函數式;并構建基于均值的權重更新函數,通過判斷子目標均值占比計算以確定各目標的最佳權重系數,從而保證算法的精度和效率。 步驟12:根據多目標計算蟻群的適應度并排序,用最優的m個蟻群更新信息素。判斷迭代次數t是否達到設定的最大迭代次數T,若未達到則令t=t+1并進入步驟2;若已達到則程序結束,并輸出最優個體。 選取某即時配送平臺實際數據進行測試分析。該平臺在一段時間內共接到6 000個訂單,由該區域內30輛同車型車提供服務,配送員的平均配送速度為25 km/h,模型參數見表2,商家和客戶的位置,預計送達時間均已知。 表2 模型參數 運用C++編程求解,設置信息啟發式因子α=1.0,期望啟發式因子β=2.0,信息素揮發系數ρ,信息素增量系數Q,螞蟻數量m=50,最大迭代次數為500次,得到基于均衡配送員工作量的配送方案如表3所示,記為方案一,其算法的迭代過程如圖4和圖5所示。 結果顯示方案一工資級差為284.910元,訂單分配量較為均衡,說明本模型能夠有效緩解收入不均、訂單量負荷過重的問題;花費的配送總成本為1 6164.372 8元,而總的超時懲罰成本僅156.681元,客戶最低滿意度為82.4%。 表3 方案一配送優化結果 由圖4可知,該算法在求解過程中共迭代了500次,在運行初期目標值下降趨勢顯著,遺傳至400代時基本收斂,最優解趨于穩定。表明該算法具有較好的尋優能力,算法收斂結果好。 由圖5可得,隨著迭代次數的增加,三個目標均呈現逐步優化的趨勢, 當最優解趨于穩定時, 配送員工資差、配送總成本和客戶最低滿意度均得到相對較優的結果。將方案一與僅考慮配送總成本的方案二、僅考慮客戶滿意度的方案三和同時考慮配送總成本和客戶滿意度的方案四進行對比分析,結果見表4。 圖4 綜合目標的算法迭代過程 圖5 單個目標的算法迭代過程 表4 計算結果對比表 與方案二相比,方案一中配送員的工資級差顯著優于方案二,降低了30.27%,超時客戶數雖略有增加,但客戶的最大超時卻明顯降低,滿意度優于方案二,同時配送總成本僅增加3.26%;與方案三相比,配送員工資級差降低了29.49%,配送總成本也低于方案三1.57%,配送時間和配送里程也均有所減少,而客戶滿意度僅稍有降低;與方案四相比,客戶滿意度略有增加,配送總成本和總里程幾乎無變化,但配送員的工資級差卻減少了16.64%。 綜上,本文構建的多目標綜合優化方案顯著優于其他幾個方案,在成本幾乎無增加的前提下,一方面大幅度提高了配送員工作量的均衡性,提高了收入與工作量的優化匹配,能夠有效緩解收入不均、員工高離職率的問題,確保配送隊伍穩定性;另一方面還能夠有效確保配送的效率和準時性,提高客戶的整體滿意度。 為驗證模型和算法的有效性,隨機生成不同數量的訂單,用MATLAB直接求最優解與本文算法求解進行比較,結果如表5所示。 表5 模型驗證與算法對比 通過比較可知,當訂單數量較小時(≤50),本文算法的結果與最優解保持一致,而當數量較大時(≥100),本文算法結果與最優解相差較小。此時求精確解的計算時長已大于2小時,而本文算法計算時長一直在10分鐘內,從而說明本文采用的混合蟻群算法是合理有效的。但由于精確算法容易形成指數爆炸,難以在規定時間求得模型最優解,因而本文采用的混合蟻群算法更適用于解決較復雜的實際配送問題。 為緩解即時配送領域出現的訂單量分配不均、員工頻繁離職等問題,本文在配送員收入均衡準則下兼顧配送成本和客戶滿意度,結合訂單具有取送貨、商家和客戶有序配對的特征,對多目標取送貨配送問題進行綜合優化研究。研究結果表明,考慮均衡配送員收入的多目標綜合優化,并不會導致配送成本的大幅增加,還能達到均衡配送員工作量和提高客戶滿意度的效果。 基于該研究結果,即時配送平臺可考慮更多因素進行派單機制的優化,能夠在不損傷現有優化目標的同時,提高配送員派單量的均衡性,進一步提高工作量與收入的適配度,可在一定程度上達到穩定配送隊伍,提高運營穩定性的效果,對促進即時配送行業的健康穩定發展具有重要意義。□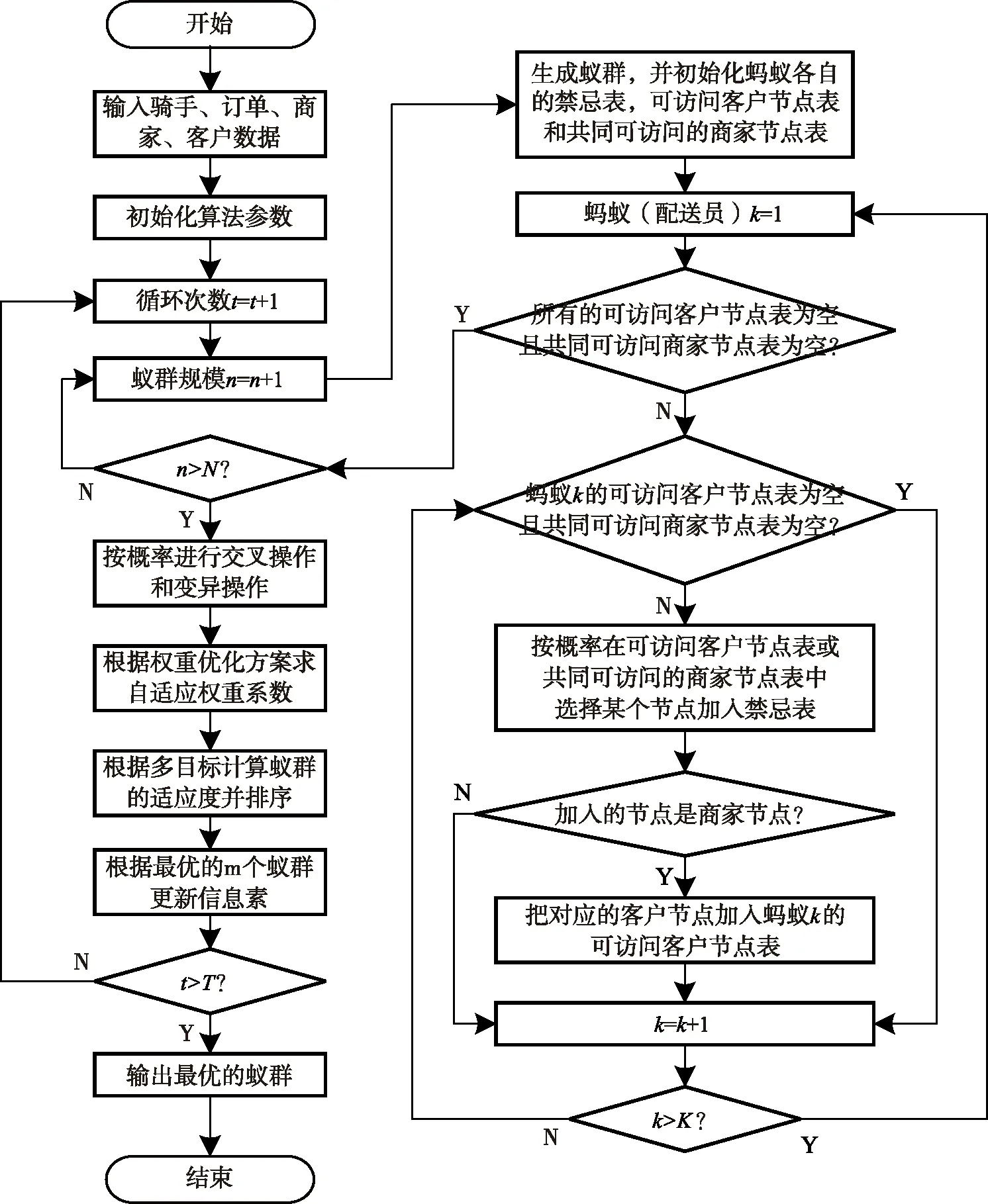
四、算例分析
(一)算例結果



(二)算法性能分析
五、結 論

