基于Python實現圓周率的三維模型研究

李毅 劉凱峰 陳巧琳 胡春兵

摘要：基于Python與蒙特卡洛算法對圓周率進行研究[1]，為了實現對圓周率更加準確的計算，需要進行大量的實驗及計算歸納，在實驗中將計算機編程技術加以運用，能夠有效降低重復運算次數[2]。根據已有二維平面模型拓展為三維模型，使實驗效果更加直觀、立體。

關鍵詞：Python;蒙特卡洛法;圓周率;三維模型

中圖分類號：TP311? ? ?文獻標識碼：A

文章編號：1009-3044（2022）10-0110-03

1 圓周率的含義及歷史

圓周率Pi是圓的周長與直徑的比值，一般用希臘字母π表示，是普遍存在數學及物理學中的數學常數（約等于3.1415926） ，也是一個無理數。它是圓的周長與直徑的比值，也等于圓的面積與半徑平方之比，π在準確計算圓周長、圓面積、球體積等問題中扮演著極其重要的角色。

圓周率散發著經久不衰的吸引力，以至于在人類幾千年的歷史長河中，許多數學家都在尋求π的值，甚至為之付出了畢生的心血。從古至今，能像圓周率一樣吸引眾多的學者的數字屈指可數，計算圓周率的值具有極其重要的含義，查閱歷史上對π的求值程度往往能反映出這個區域甚至這個時代數學發展的大致水平。

圓周率π在計算界占有重要的地位，縱觀古今中外歷史，我們可以將圓周率計算方法的發展史大略分為四個時期[3]：實驗時期、幾何法時期、分析法時期、計算機時期。電子計算機的迅速普及使π值計算有了日新月異的進展，計算圓周率π值的方法和求解速度都實現了前所未有的突破，使對π的求值運算步入了一個嶄新的發展期，圓周率π的數值達到了難以想象的精度。

2 采用的工具

隨著近代計算機技術的發展，蒙特卡洛方法也因自身的特性而得到廣泛應用。蒙特卡洛方法現已成為人們處理復雜的數據建模和更高維度問題的主要工具，它在電子學、生物學、高分子化學，近似計算等學科與方法的研究中有著重要的應用[4]。通過科學合理的統計建模，把較為復雜的研究對象，轉化成對隨機數及其數字特征的模型及運算，從實質上簡化了研究問題，減少了運算的復雜性，從而獲得最佳的近似解[5]。

大數定理則是蒙特卡羅法最為關鍵的數理基石，如果要使用蒙特卡羅方法來求解問題，則需要重復大量同樣的實驗，只有實驗次數足夠多，所獲得的結論才會接近于真實值。蒙特卡洛法的本質是構造出一個具有隨機性的問題，并使數學上推導出來的結論正好是所求問題的解，多次重復實驗后，求得問題的多個解，即可獲得近似的結果[6]。

現在計算機技術飛速發展，編程語言早已是計算機應用軟件開發中不可或缺的一部分，Python編程語言擁有編寫簡潔快速、語法優美易讀等優勢，在各領域都能看得到它的身影[7]。本文將Python的諸多優勢融入實驗過程中，既可以清晰明了地展現出實驗的結果，又能夠使學習者更加注重問題的思想本質，而不是煩瑣的代碼。除此之外，使用Python 語言還能輕松簡潔地編寫圖形界面程序[8]，大大降低了本次研究的難度。

3 二維模型建立

首先通過二維平面圖像來介紹實驗過程，研究表明可以通過圓和正方形的面積計算公式得到圓面積=正方形的面積*（圓中的點/正方形中的點） 。實驗中，本文選擇一個含有內切圓且邊長為2的正方形，如圖1所示，向其中投射大量的針，每根針在正方形上形成一個“投點”，依靠投點在內切圓的個數與正方形內投點個數的比值等于Pi/4，再進行簡單地變換就得到Pi的值。為保證實驗結果的精確度，投點總數通常較大，由于計算落在圓內投點數顯得較為困難，故可以運用Python及蒙特卡羅算法的來協助探究。

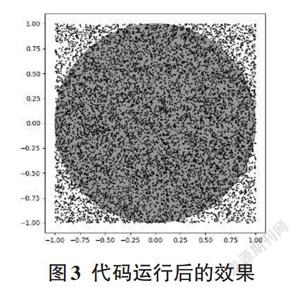
使用Python代碼來實現上述過程，如圖2所示，需要定義N代表投點的總個數，n代表投射在內切圓中小點的總個數，用兩個從-1到1之間的隨機值來代表投點的橫坐標和縱坐標，并創立兩個列表分別來記錄橫坐標和縱坐標的值，然后利用公式求得Pi值并用列表記錄。調用畫圖工具將實驗過程呈現出來，得到如圖3所示。

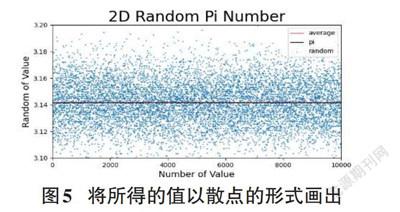
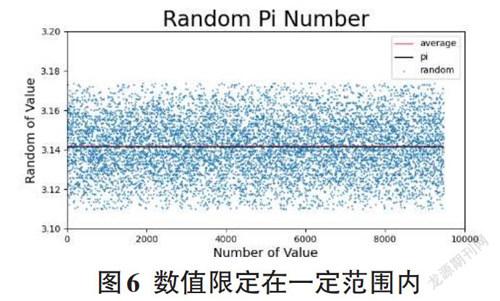
接著通過調用數學函數將列表之中大量的實驗結果所求Pi值取平均值、方差及標準差，將所有Pi值放進圖中形成散點圖，同時將Pi的平均值畫成一條紅線與Pi的原值（3.1415926） 畫出的黑線相對比就可以發現紅線和黑線幾乎重疊，如圖5所示，證明所用的方法是比較合理的。如果做一個領域半徑r來剔除出實驗所求Pi的異常值，即可使實驗數據更加精確，方差和標準差都會縮小，所求的值離Pi的真實值更接近，如圖6所示。

4 三維模型建立

根據二維的平面模型可以延伸到三維的立體模型，三維模型的實驗數據將比二維模型的實驗數據更加合理。與二維模型相比，三維模型具有更多優勢，三維模型的空間信息呈現更直接，三維模型給空間信息提供了更為豐富展示空間，而且三維模型在可視化方面有著巨大的優勢[9]。實驗中二維模型轉化為三維模型即是將邊長為2的正方形內切圓轉化為邊長為2的正方體內切球，如圖8所示，投射針將要從正方體的多個方向發射，確保“投點”在三維的坐標系下分布均勻。同理，經過簡單的數學公式推導變化，使用內切球和正方體的體積公式與投點在球內和正方體內的比值等于Pi/6，最后就能得到Pi的值，如圖7中公式所示。

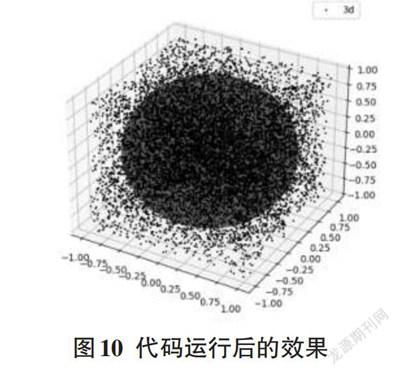
使用Python代碼來實現三維模型的圖像，同樣需要定義N代表投射點的總個數，n則代表投射在內切球體之中小點的總個數，用三個從-1到1之間的隨機值來代表投點所在的坐標（即x軸，y軸和z軸） 就能近似地認為投射在一個邊長為2的正方體內，并創立三個列表來分別記錄這些坐標，然后利用公式求得Pi值并用列記錄。最后利用畫圖工具將整個實驗過程呈現出來，如圖10所示。

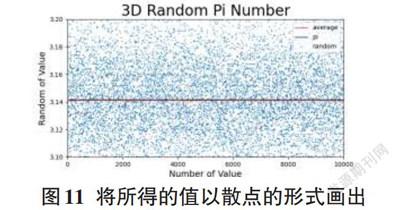
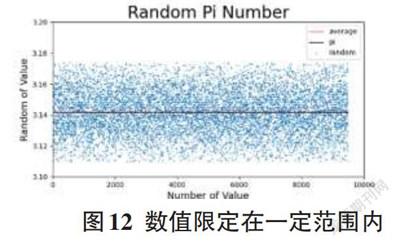
將二維模型求出Pi近似值的方法略做修改即可等價地將三維模型Pi的近似值求出，如圖7中公式所示，利用數學函數將三維模型實驗所求大量Pi值取平均值、方差和標準差，將實驗中產生的大量Pi值都放進圖中形成散點圖，并將這些值的平均值畫成一條紅線與Pi的真實值（3.1415926） 畫出的黑線相對比，如圖11所示。使用相同的坐標刻度，可以清晰地對比二維圖形和三維模型的精確程度。同理，對三維模型實驗數據大量Pi值做一個領域半徑r，來剔除異常實驗數據值Pi，可以讓數據更加精確，方差和標準差都會縮小，所求的平均值離Pi的真實值更接近，如圖12所示。

5 總結

即使近現代計算機技術高速發展，然而對圓周率π的求值并沒有停止，計算仍在繼續，但它已經不再被用在日常生活之中，研究的π意義已經不再局限于簡單的數值計算，一方面基于個人的興趣愛好，另一方面被用來檢測計算機性能的好壞以及公式的優劣。現如今，圓周率往往不再是一種被檢驗的對象，而是同最大素數相類似地被當作檢測工具，兩者皆用于檢測設備的先進程度和算法的優劣。

在本次研究中，使二維平面模型轉化為三維立體的模型，是秉持逐步向高緯度空間探索的精神。想要探索四維甚至更高維空間，就需要先投影到三維世界來看，將二維模型拓展到三維模型是不可或缺的一部分。人類向高維度的探求是科學發展以來的永恒目標，假設擁有足夠的數學知識，從眾多三維模型中得到啟發，極有可能帶動科學研究邁出一大步。

參考文獻：

[1] 何光.用蒙特卡羅方法計算圓周率的近似值[J].內江師范學院學報，2008，23（4）：14-16.

[2] 王玉華，李嬌，方曙東.基于Python實現圓周率的蒙特卡羅算法的研究[J].池州學院學報，2019，33（3）：17-18.

[3] 張曉貴.圓周率計算的四個時期[J].遼寧教育學院學報，2000，17（5）：66-69.

[4] 朱陸陸.蒙特卡洛方法及應用[D].武漢：華中師范大學，2014.

[5] 楊筱珊.蒙特卡羅方法在定積分近似計算中的應用[J].安順師專學報（自然科學版），1998（2）：34-40.

[6] 李姣娜.蒙特卡羅方法的原理及在數值計算方面的應用——以定積分為例[J].濰坊工程職業學院學報，2018，31（5）：104-108.

[7] 姚建盛，李淑梅.Python在科學計算中的應用[J].數字技術與應用，2016（11）：76.

[8] 程麗玲.淺談Python在科學計算中的應用[J].信息系統工程，2018（10）：55.

[9]徐鵬飛，丁榆城，張煒，等.基于三維CAD造型內螺旋銑刀精確建模[J].中國機械，2019（17）：1.

【通聯編輯：梁書】

收稿日期：2021-11-28

基金項目：四川民族學院瀘定校區校園網建設關鍵技術研究（XYZB2009ZB） ;四川民族學院基于微信小程序的食堂在線預約系統研究（XYZB2008ZB）

作者簡介：李毅（1990—） ，男，四川巴中人，碩士研究生，助教，研究方向為最優化算法。