圓柱體垂直入水三維數值模擬及影響因素研究

鄒田春， 高 飛， 魏家威， 解 江

(中國民航大學 適航學院，天津 300300)

結構物入水沖擊涉及氣-固-液三者之間的相互作用，是典型的流固耦合過程，在結構入水過程中，結構與自由液面沖擊產生的較大沖擊力極易導致外部結構破損，內部構件的失效，返回艙入水、魚雷入水、水上飛機的起降等都屬于結構入水的范疇。因此結構物入水的研究在軍事、船舶、海洋工程、航空航天等領域都有重要的工程應用背景。

近十年來研究人員針對結構入水沖擊問題的分析研究大多以楔形體[1-4]、圓柱體[5-8]、球體[9-10]等作為研究對象，采取試驗和仿真方法開展研究。Shah進行了剛性楔形體入水沖擊試驗，利用高速攝像成功捕捉到了整個二維流體流動動態過程，并運用光滑粒子流體動力學(smoothed particle hydrodynamics，SPH)方法建立相應模型，對SPH方法模擬結構入水的準確性進行了驗證。夏維學等以圓柱體為研究對象開展入水試驗研究，對入水空泡壁面運動特性與空泡演化過程之間的關系進行分析，并基于空泡壁面運動特性劃分空泡演化各階段，分析了空泡演化在各階段的流動機制。Luo等[11]對三維鋼質楔形體進行了一系列自由落體入水沖擊試驗，研究楔形體入水沖擊加速度、壓力及應力響應，并建立了楔形體試驗件的有限元模型，通過在模型上施加試驗測得的入水沖擊壓力來預測結構的瞬態響應，并對水彈性效應進行討論。施書文等[12]針對入水抨擊問題提出了一種弱可壓光滑粒子水動力與光滑點插值流固耦合法，運用該方法計算了彈性斜板低速入水和楔形體高速入水問題，計算結果與試驗值和半解析解吻合良好，證明了該方法對模擬彈性體入水問題的有效性。結構入水仿真方法主要有有限體積法(finite volume method，FVM)[13-17]、SPH方法[18-20]以及任意拉格朗日歐拉(arbitrary Lagrangian-Eulerian，ALE)方法[21-26]等。ALE方法兼具拉格朗日法和歐拉法的優點，在結構入水問題研究領域采用較多且較為成熟。在傳統ALE理論和算法不變的情況下，S-ALE(structured-arbitrary Lagrange-Euler)方法則利用網格的規律性，將ALE模型規則網格通過輸入三維點位坐標方式由程序本身自行創建網格，極大降低數值模擬的計算成本。

針對結構入水問題的研究，在國防、軍事上大多以楔形體為研究對象，當前我國正在大力發展民用客機且目前民用大型客機都是典型筒段機身結構，考慮到民機機身水上迫降的工程背景，本文選擇圓柱體為研究對象。基于圓柱體垂直入水沖擊試驗研究結果，本文建立了圓柱體三維數值模型，采用S-ALE算法對圓柱體垂直入水沖擊過程進行了數值模擬，分析其入水沖擊響應特性，并通過對比圓柱體入水位移及自由液面動態變化來驗證模型有效性；基于驗證的數值模型，進一步研究圓柱體入水速度、質量和長度對其垂直入水沖擊的影響規律。

1 基本理論

1.1 S-ALE基礎方程

S-ALE在實現上是獨立于ALE而全新開發的，程序簡潔高效，但在理論方面S-ALE求解器與ALE完全相同。在ALE方法的描述中，引入了除Lagrange和Euler坐標系之外的第三個任意參照坐標系，與參照坐標相關的材料微商可以采用式(1)描述

(1)

式中：Xi為Lagrange坐標；xi為Euler坐標；wi為相對速度。

假設物質速度為v，網格速度為u，引入相對速度w=v-u。則ALE方法的控制方程可以由如下守恒方程給出

(1)質量守恒方程

(2)

(2)動量守恒方程

控制固定域內的牛頓流體流動問題的增強形式由控制方程和對應的初始及邊界條件組成，控制流體問題的方程是Navier-Stokes方程的ALE描述

(3)

應力張量為

σij=-pδij+μ(vi,j+vj,i)

(4)

式中：p為壓強；bi為單位質量的體積力；δij為Kronecker δ函數；μ為動力黏性系數。該方程可與下列邊界條件和初始條件聯立求解

(5)

σijnj=0,Γ2邊界

(6)

Γ1∪Γ2=Γ,Γ1∩Γ2=0

(7)

式中：Г為計算域的完整邊界，分為Г1和Г2兩個部分，其中，Г1為固體邊界，Г2為自由液面邊界[27]；上標0為該參數的初始指定值；nj為邊界的外法線單位向量。假設整個計算域在t=0時刻的速度場是靜止的，即

vi(xi,0)=0

(8)

(3)能量守恒方程

(9)

采用算子分離法求解ALE方程，該方法將每個時間步分為兩個階段。首先執行拉格朗日過程，此時網格隨物質一起運動。該過程計算速度、內外力引起的內能改變量，平衡方程為

(10)

(11)

單元邊界沒有物質流過，所以滿足質量守恒。第二個計算階段為對流階段，在對流階段之前采用VOF(volume of fluid)方法捕捉不同材料之間的界面位置，然后對穿過單元邊界的質量運輸、內能以及動量進行計算，即將拉格朗日階段的移位網格重映射回初始位置或者任意位置。

對于每個節點，速度和位移按下列等式進行更新

(12)

xn+1=xn+1+Δtun+1/2

(13)

外力矢量又分為體積力、邊界力、非反射邊界條件及接觸力。本文采用標準罰函數算法計算流體與結構之間的接觸力。罰函數算法中允許從節點穿透到主段，所以在每一個時間步，系統首先檢查從節點是否穿透主面，未穿透前，不做任何處理，當發生穿透，則引入一個與穿透距離d成比例的界面接觸力F并將其分配到流體單元節點上，計算公式為

F=ki·d

(14)

式中,ki為基于主從節點質量模型特性的剛度系數。

1.2 水和空氣狀態方程

圓柱體垂直入水模型中，水和空氣采用空材料模型，通過一個截斷壓力值來定義壓力的更小邊界值，式(15)為任意方向黏性應力的表達式。通過狀態方程來定義壓力，其中水采用Gruneisen狀態方程，空氣采用Polynomial狀態方程。

(15)

Gruneisen狀態方程對于壓縮材料由式(16)計算，膨脹材料由式(17)計算。

(γ0+au)E

(16)

P=ρ0C2u+(γ0+au)E

(17)

式中：C為沖擊波速度；E為流體的比內能；ρ0為流體密度；γ0為Gruneisen伽馬；a為對γ0的一階體積修正；S1，S2，S3為曲線斜率的系數；由于材料不受初始載荷，初始能量項E和修正因子a均設為1。

線性多項式狀態方程

P=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+C6μ2)E

(18)

式中：C0，C1，C2，C3，C4，C5，C6為自定義的常數；E為單位初始體積的內能。

水的Gruneisen狀態方程參數，如表1所示。空氣的Polynomial狀態方程參數，如表2所示。

表1 水的Gruneisen狀態方程參數Tab.1 Parameters of Gruneisen state equation for water

表2 空氣的Polynomial狀態方程參數Tab.2 Parameters of Polynomial state equation for air

2 有限元建模

圓柱體垂直入水三維模型，如圖1所示。圓柱體直徑D=160 mm，長L=295 mm；水和空氣域長L=810 mm，寬W=660 mm，高H=700 mm其中水深h=480 mm。模型采用實體單元建模，圓柱體采用Lagrange單元，空氣和水采用Euler單元。通過定義ALE_STRUCTURED_MESH_CONTROL_POINTS和ALE_STRUCTURED_MESH兩個關鍵字在計算過程中由程序自動生成水和空氣的網格。

為防止圓柱體在試驗過程中發生變形，將PVC圓柱體內部用泡沫材料進行實心填充，所以圓柱體采用剛體進行建模。水和空氣采用NULL材料模型和流體狀態方程來模擬，并對模型施加向下的重力加速度g，可以產生水的壓力梯度。

約束流體域底面單元節點的所有自由度來模擬水池底面邊界條件；在流體域四周設置無反射邊界條件，模擬無限水域，可減小流體域大小，降低計算成本，還可防止邊界產生的反射波與結構發生流固耦合作用。運用S-ALE罰函數耦合算法計算圓柱體與流體之間的耦合作用。

基于Russo等開展的圓柱體入水試驗結果，選取質量為m0(2.214 kg)試驗件提升1 m高度的入水試驗工況，如圖2所示。作為本文圓柱體入水沖擊仿真的初始工況。初始時刻圓柱體距液面高度為零，圓柱體初始入水速度為v0，通過運用GetData Graph Digitizer確定初始入水速度v0為3.6 m/s。將圓柱體入水沖擊仿真結果與試驗結果進行對比驗證。

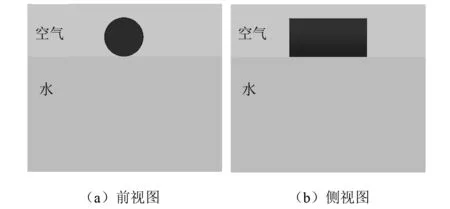
圖1 數值模擬模型Fig.1 Numerical simulation model

圖2 不同質量試驗件提升高度與入水時刻速度關系圖Fig.2 Relation diagram of lifting height and water entry velocities of test pieces with different masses

3 有限元仿真及驗證

3.1 S-ALE與ALE計算對比

采用10 mm網格分別建立ALE模型和S-ALE模型，圓柱體與空氣、水網格比例為1 ∶1，設置計算總時長為0.25 s，使用LS-DYNA 971求解器在主頻為2.8 GHz的工作站上采用8核進行計算。兩種模型在相同設置和工況下計算時間與最大位移值，如表3所示。S-ALE模型計算時間相對于ALE模型減少了20.2%。兩種模型計算得到的圓柱體位移-時間曲線對比，如圖3所示。從圖3可知，變化趨勢完全一致。其中，ALE模型得到最大位移值為0.231 6 m，S-ALE模型得到最大位移值為0.231 8 m，兩者相差可以忽略不計。因此，S-ALE模型在獲得相同仿真精度條件下可以大大減少計算時間。

表3 計算時間及最大位移值Tab.3 Calculation time and maximum displacement

圖3 S-ALE模型與ALE模型仿真結果對比Fig.3 Comparison of simulation results between S-ALE model and ALE model

3.2 模型驗證

圓柱體與空氣、水的網格尺寸相同，分別選取7.5 mm、10 mm、15 mm和20 mm進行計算。采用S-ALE模型獲得的圓柱體入水位移-時間曲線與試驗結果對比，如圖4所示。

隨著網格的細化，仿真獲得的圓柱體最大位移值增加，且更接近試驗最大位移值(0.241 m)；網格細化到10 mm時，仿真獲得的圓柱體最大位移值趨于穩定。當網格尺寸為10 mm時，圓柱體最大位移值為0.231 m，與試驗值相差4.15%；網格尺寸為7.5 mm時，圓柱體最大位移值為0.235 m，與試驗值相差2.49%。因此，選用7.5 mm網格尺寸，模型總網格數為898 372，圓柱體不同入水時刻獲得的仿真位移值與試驗值對比情況，如表4所示。位移誤差均在3%以內，因此S-ALE模型能夠精確模擬圓柱體入水位移時間歷程。

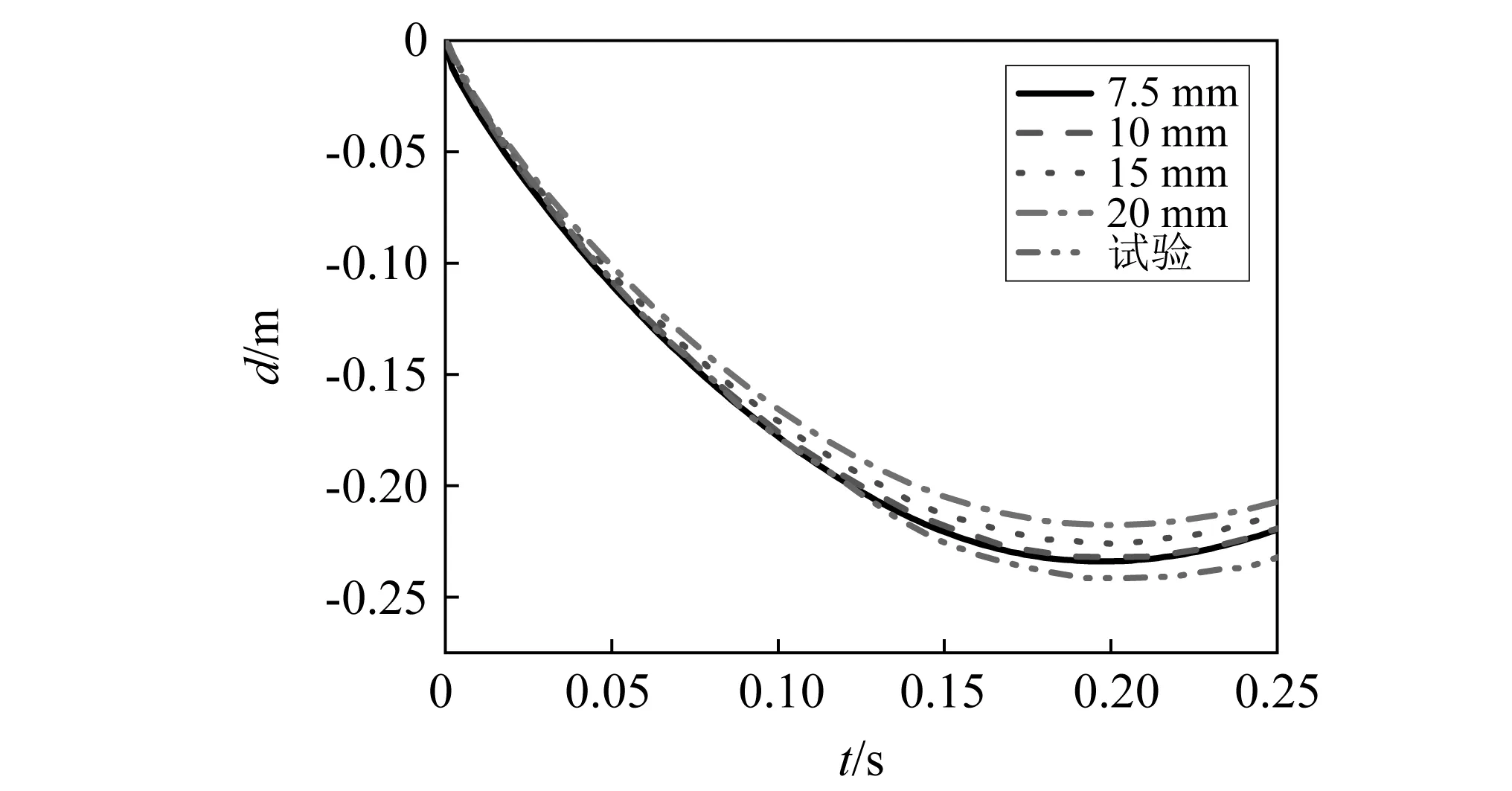
圖4 不同網格大小計算結果與試驗結果對比Fig.4 Comparison of calculation results of different grid sizes and test results

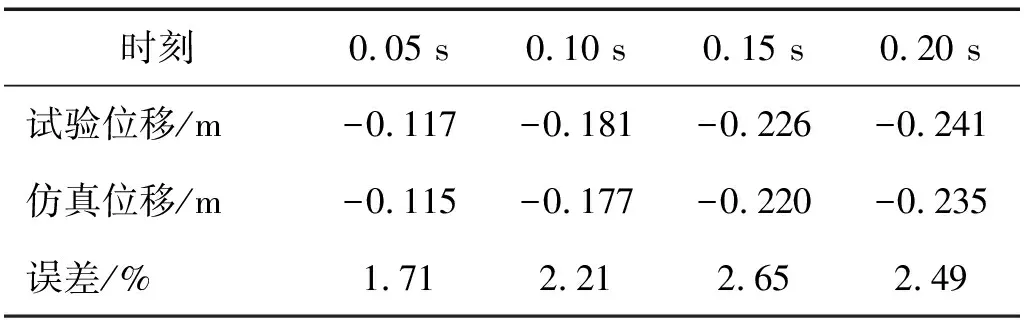
表4 不同時刻圓柱體仿真位移值與試驗結果對比Tab.4 The simulated displacement value of cylinder at different times compared with the experimental results

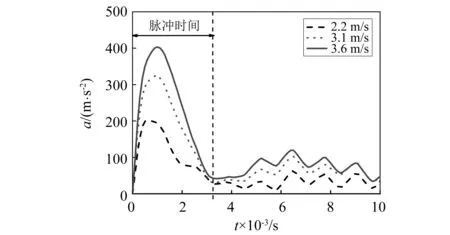
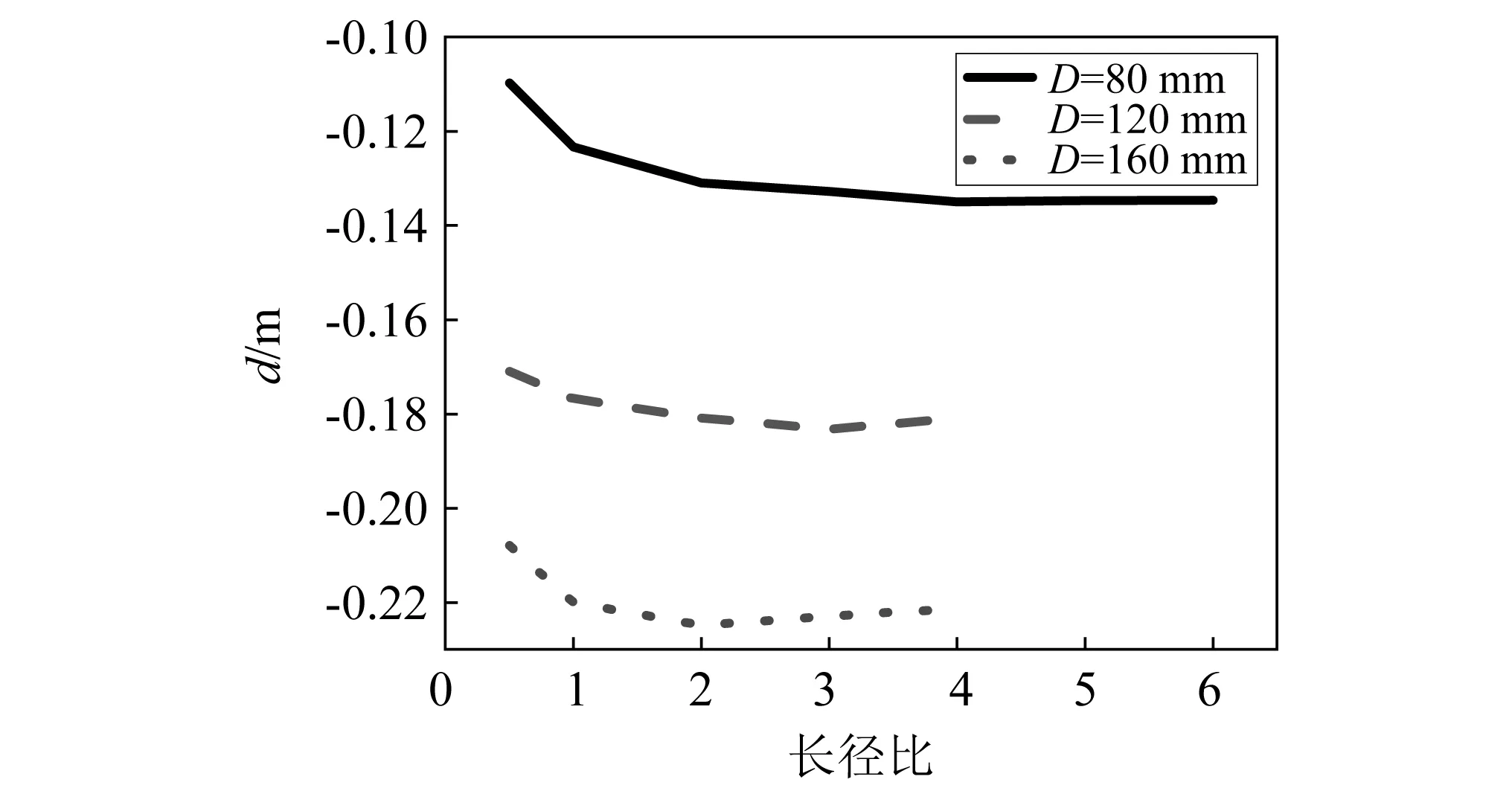
圓柱體入水仿真結果與試驗結果對比,如圖5所示。當圓柱體接觸到自由液面時，圓柱體動能開始轉移為水的動能，圓柱體所擠占空間處的水在接觸處被噴射出來形成射流；圓柱體在下沉過程中高速的自由液面射流不斷增長與擴大(T<τ/5)(τ為圓柱體達到最大向下位移的時刻)；在(τ/5)

圖5 仿真結果和試驗結果對比Fig.5 Comparison of simulation and experimental results

S-ALE模型計算得到的液面運動情況與試驗之間有微小的差異，對于射流的飛濺效果，模擬結果不如試驗明顯，但仿真模擬基本上再現了圓柱體撞擊水面、自由液面射流形成、空氣腔打開、空氣腔閉合的典型現象。整體來看自由液面動態仿真模擬結果與試驗基本一致。

3.3 圓柱體入水速度分析

7.5 mm尺寸網格模型仿真得到的圓柱體入水速度變化曲線,如圖6所示。從圖6可知，圓柱體入水整個運動過程可分為撞擊水面、減速下移和上浮三個階段。圓柱體在撞擊水面時受到較大沖擊載荷，速度迅速下降，由于圓柱體密度小于水，在沖擊波衰減過后，其受水的作用力仍大于重力，因此圓柱體在撞擊水面后做加速度相對較小的減速運動，并在0.198 s時速度減小到0，此時圓柱體在水中處于懸浮狀態，隨后在浮力的作用下圓柱體開始上浮。

圖6 圓柱體入水速度-時間曲線Fig.6 Velocity-time history curve of cylinder water entry

4 不同因素影響研究

4.1 圓柱體入水速度影響

圓柱體(D=160 mm，L=295 mm)不同入水速度下的加速度-時間歷程曲線，如圖7所示。從圖7可知，三種速度下加速度曲線都有一較大峰值，此時段為圓柱體沖擊水面時段，在較大沖擊載荷作用下會對結構產生較大破壞，也是結構物入水研究關注的重點，對比加速度曲線可知，入水速度對圓柱體加速度峰值影響非常明顯，隨著速度的增大加速度峰值增大，而對加速度脈沖持續時間幾乎沒有影響。

圖7 圓柱體不同入水速度加速度-時間曲線Fig.7 Acceleration-time history curves of cylinder with different water entry velocities

圓柱體(D=160 mm，L=295 mm)在不同速度下的入水位移-時間歷程曲線，如圖8所示。從圖8可知，三種速度下圓柱體位移趨勢一致，隨著入水速度增大，圓柱體向下運動的越快且最大位移增大，但達到最大位移的時刻基本保持不變。

圖8 圓柱體不同入水速度位移-時間曲線Fig.8 Displacement-time history curves of cylinder with different water entry velocities

4.2 圓柱體質量影響

通過在圓柱體上方增加集中質量的方式改變圓柱體質量從而獲得2.214 kg，3.214 kg，4.214 kg，5.214 kg圓柱體入水沖擊加速度。圖9為圓柱體(D=160 mm，L=295 mm)入水速度3.6 m/s，不同質量工況下加速度曲線，如圖9所示。從圖9可知，隨著質量增大，加速度峰值有減小趨勢，但質量增加未改變加速度脈沖持續時間。圓柱體受力示意圖如圖10所示。由牛頓第二定律式(19)可以得到圓柱體入水沖擊在垂直方向上所受水的合外力F(包括浮力、動量傳輸引起的附加力、形狀阻力)，不同質量圓柱體入水所受阻力曲線，如圖11所示。由圖11可知，在圓柱體外形不變的條件下不同質量圓柱體入水沖擊所受水的合外力基本不變，則由式(20)可知，外形相同的圓柱體入水沖擊時，質量m越大，加速度a越小。

F-mg=ma

(19)

a=F/m-g

(20)

式中：m為圓柱體質量；g為重力加速度；a為圓柱體加速度。

圖9 不同質量圓柱體入水加速度-時間曲線Fig.9 The water entry acceleration-time history curves of cylinders with different masses

不同質量圓柱體(D=160 mm，L=295 mm)以2.2 m/s速度入水時位移-時間歷程曲線，如圖12所示。從圖12可知，由于加速度大小與質量呈負相關，則質量越大圓柱體入水減速越緩，向下運動的越快；隨著質量增加，圓柱體入水最大位移及其到達時刻都增大；當質量增加到圓柱體重力大于浮力時，圓柱體入水過程最終將會達到穩定狀態，保持勻速一直下落。

圖10 圓柱體入水沖擊時的受力圖Fig.10 The force diagram of cylinder impact water

圖11 不同質量圓柱體入水所受阻力曲線Fig.11 The water entry drag force curves of the cylinders with different masses

圖12 不同質量圓柱體入水位移-時間歷程曲線Fig.12 The water entry displacement-time history curves of cylinders with different masses

4.3 圓柱體長度影響

為研究圓柱體入水三維效應，針對給定直徑D的圓柱體，保持其密度ρ不變，只改變長度L，研究長度對圓柱體入水特性的影響。

選取D=160 mm圓柱體，不同長度圓柱體入水加速度-時間歷程曲線，如圖13所示。不同長度(D=160 mm)圓柱體加速度峰值大小，如圖14所示。從圖14可知，加速度峰值隨著長度的增大而增大，且當L/D>1時，增加趨勢逐漸變緩，當L/D>3時，L/D的增加對加速度峰值幾乎沒有影響。L/D對加速度脈沖持續時間幾乎沒有影響。相對于速度，長度改變所造成的加速度變化幅度明顯要小。

圖13 不同長度(D=160 mm)圓柱體入水加速度-時間曲線Fig.13 The water entry acceleration-time history curves of cylinders(D=160 mm)of different lengths

圖14 不同長度(D=160 mm)圓柱體入水加速度峰值Fig.14 The water entry peak accelerations of cylinders (D=160 mm) with different lengths

不同長度(D=80 mm)圓柱體入水位移-時間歷程曲線，如圖15所示。從圖15可知，隨著L/D增大，圓柱體最大入水位移與其達到最大位移的時刻都增大；當L/D>2時，L/D的增大對最大位移的影響逐漸降低；當L/D>4時，L/D的增加不再影響最大位移。

圖15 不同長度(D=80 mm)圓柱體入水位移-時間曲線Fig.15 The water entry displacement-time history curves of cylinders(D=80 mm)with different lengths

不同長度(D=120 mm)圓柱體入水位移-時間歷程曲線，如圖16所示。當L/D<3時，隨著L/D的增加，圓柱體最大入水位移與其達到最大位移的時刻都增大；當L/D>3時，隨著L/D的增加，最大入水位移開始減小。

圖16 不同長度(D=120 mm)圓柱體入水位移-時間曲線Fig.16 The water entry displacement-time curves of cylinders(D=120 mm)with different lengths

圖17給出了不同長度(D=160 mm)圓柱體入水位移-時間歷程曲線，當L/D<2時，圓柱體最大入水位移與其達到最大位移的時刻都增大；當L/D>2時，隨著L/D的增加，最大入水位移逐漸減小。

圖17 不同長度(D=160 mm)圓柱體入水位移-時間曲線Fig.17 The water entry displacement-time curves of cylinders(D=160 mm)with different lengths

L/D對圓柱體入水的影響在開始時間階段較小，且L/D越小向下運動的越快，隨著向下運動的進行，L/D對圓柱體位移的影響變的更加明顯，且因直徑的不同而呈現不同的規律。

圓柱體最大入水位移與不同L/D的關系曲線，如圖18所示。從圖18可知，隨著直徑的增大，最大位移增大；三種直徑圓柱體，在L/D<2時，L/D對位移的影響較大；當L/D>2時，影響逐漸變緩，且不同直徑呈現不同的影響規律。

圖18 不同長度、不同直徑圓柱體入水位移曲線Fig.18 The water entry displacement curves of cylinders with different lengths and diameters

5 結 論

(1)相對ALE模型，S-ALE模型在保證計算精度的前提下，可大大提升計算效率。S-ALE模型可以完整的再現圓柱體沖擊水面、自由液面射流形成、空氣腔打開、空氣腔閉合的整個過程。通過圓柱體入水過程典型時刻自由液面動態以及位移的數值計算結果與試驗結果對比，驗證了本文所建立模型的有效性和準確性。

(2)隨著圓柱體入水沖擊速度的增大，圓柱體加速度峰值及最大位移值都增大，但對加速度脈沖持續時間和達到最大位移時刻沒有影響。

(3)加速度大小與質量呈負相關，但圓柱體質量改變，加速度脈沖持續時間基本不變，質量增大最大位移及其到達時刻增大。

(4)長度增加，圓柱體入水沖擊加速度增加，但對加速度脈沖持續時間沒有影響，且相對于速度，長度改變引起的加速度變化幅度明顯要小；入水位移在開始時間段受長度的影響較小，且L/D越小圓柱體向下運動的越快，隨著圓柱體向下運動的進行，L/D對圓柱體位移的影響變的更加明顯，且因直徑的不同而呈現不同的規律。