基于高斯展開法的周期聲學黑洞寬頻能量回收特性研究

宋婷婷， 鄭 玲， 鄧 杰

(1.重慶大學 汽車工程學院，重慶 400044；2.重慶大學 機械傳動國家重點實驗室，重慶 400044)

聲學黑洞作為一種新型的波動控制方法，在振動噪聲控制、聲波調控以及能量回收領域，受到國內外學者的廣泛關注[1-2]。聲學黑洞效應是通過改變結構阻抗，使彎曲波的相速度與群速度逐漸衰減。在薄板以及梁結構中，通常是對結構厚度進行冪律剪裁，使彎曲波的相速度在結構尖端急劇減小而無法發生反射，從而實現振動能量在尖端位置的聚集。

由于其結構特殊性，聲學黑洞的振動響應很難獲得解析解，這給聲學黑洞的理論研究帶來了較大的困難。針對這一問題，Tang等[3]提出一個半解析模型來分析嵌入聲學黑洞結構的歐拉伯努利梁的振動響應。研究表明，半解析模型與有限元以及試驗結果高度一致。鄧杰等[4]采用Morlet小波作為半解析模型里的擬合函數，建立了一維聲學黑洞梁的解析模型，通過分析梁上的能量密度分布，驗證了尖端部分對于聲學黑洞能量聚集效應的關鍵作用。曾鵬云等[5]采用相同的半解析模型，研究了一維圓錐形聲學黑洞的能量聚集效應，并通過對比驗證了圓錐形聲學黑洞與楔形聲學黑洞具有相似的振動抑制效果。為了更好地展現能量在聲學黑洞結構中的傳遞過程，Wang等[6]建立了基于能量方程與Rayleigh-Ritz方程的半解析模型，對一維聲學黑洞梁進行了功率流分析，驗證了設置在黑洞尖端的阻尼層對聲學黑洞效應的加強效果。黃薇等[7]也利用功率流分析方法對二維聲學黑洞開展研究，并通過試驗驗證了聲學黑洞結構對彎曲波的聚集效應。此外，學者們以工程實踐為背景，將聲學黑洞應用到了減振降噪領域。例如：劉波濤等[8]將聲學黑洞與聲學超結構相結合，實現了低頻寬帶的高效隔聲；王小東等[9]為了彌補聲學黑洞會削弱結構強度的局限性，將其以附加粘貼的方式引入直升機的后隔板，實現了駕駛艙內良好的降噪效果；趙業楠等[10]通過引入聲學黑洞俘能器，使目標船艙室的噪聲降低10 dBA。

由于聲學黑洞結構具有振動能量的聚集效應，因此也被引入到了能量回收系統當中。此前，應用于板梁結構能量回收系統的壓電建模架構，已被國內外學者廣泛研究[11-12]。例如：汪恒等[13]將嵌入聲學黑洞結構的薄板引入到壓電俘能器中，通過在時域上與均勻板的比較，驗證了聲學黑洞結構對提高系統能量轉換效率的有效性；Zhao等[14]通過在單根梁上嵌入多個聲學黑洞結構，彌補了寬帶激勵下需要確認回收位置的限制，從結構優化上實現了能量的寬頻回收；梁玉坤[15]構造了上下對稱的復合聲學黑洞梁結構，獲得了比傳統聲學黑洞更好的結構剛度與強度，并探究了壓電材料參數對于能量回收的影響；Ji等[16]考慮到了聲學黑洞的波長壓縮特性，為了避免在壓電材料中形成正負電荷相互抵消的情況，采用寬度遠小于最小半波長的微壓電矩陣，評估了聲學黑洞量在瞬態以及穩態響應下的能量回收性能；Deng等[17]基于能量法建立了雙壓電晶片聲學黑洞懸臂梁的半解析模型，并研究了截斷厚度、壓電位置及厚度等系統參數對于能量回收性能的影響；Zhao等[18]以嵌入了3個二維聲學黑洞結構的薄板為研究對象，進行了能量回收試驗，通過與均勻薄板的對比試驗，驗證了聲學黑洞結構對能量回收的優化效果。

由上述研究可以看出，單個聲學黑洞通常只能在某些頻率點上展現出能量回收的提升效果，而周期聲學黑洞結構卻能夠通過壓縮共振峰使其在寬頻范圍內實現能量回收。但目前卻缺乏相關研究揭示周期化、幾何構型等系統參數對于能量回收共振峰的調控機理。針對這些問題，本文以周期聲學黑洞梁為研究對象，對耦合壓電晶片的聲學黑洞結構建立了半解析計算模型，依據計算結果分析了系統輸出功率及能量采集效率，揭示了周期數、黑洞半徑、中心截斷以及冪指數對于能量回收效應的影響機理，為周期聲學黑洞的寬頻能量回收奠定理論基礎。

1 耦合壓電層的能量回收數學建模

1.1 聲學黑洞理論基礎

傳統的一維聲學黑洞結構，其黑洞區域內的截面厚度與長度關系按冪函數變化，即h(x)=εxm(m≥2)。利用幾何聲學求解彎曲波在黑洞區域的彎曲振動方程時，近似假設方程的解可以表達為如下的復數形式

w(x)=A(x)eiΦ(x)

(1)

式中，A(x)與Φ(x)=kpφ(x,y)分別為結構撓度變化的幅值與相位，kp為均勻部分的波數，φ(x,y)為程函。將假設的解帶回波動方程并令實部與虛部均等于零，即可得到

k(x)=121/4kp1/2(εxm)-1/2

(2)

式中，k(x)為變截面處的彎曲波波數。相位則可以寫成梁上任意一點到黑洞尖端對k(x)的積分，即

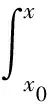
(3)

由式(3)可知，當x=0且m≥2時，相位將趨于無窮大，也就是說，彎曲波從入射端傳遞到黑洞尖端所需的時間是無窮大，即彎曲波無法傳播到尖端邊界，也就無法在邊界發生反射。因此，結構的振動能量被集中在了黑洞結構尖端，在此處布置能量回收器件，則可以高效的將振動能量轉換為電能。

1.2 基于高斯展開的耦合壓電層能量回收模型

為了研究各結構參數對于能量回收效率的影響機理，基于高斯展開法，建立耦合壓電材料的聲學黑洞能量回收半解析模型。其中，單胞聲學黑洞結構的幾何模型，如圖1所示。

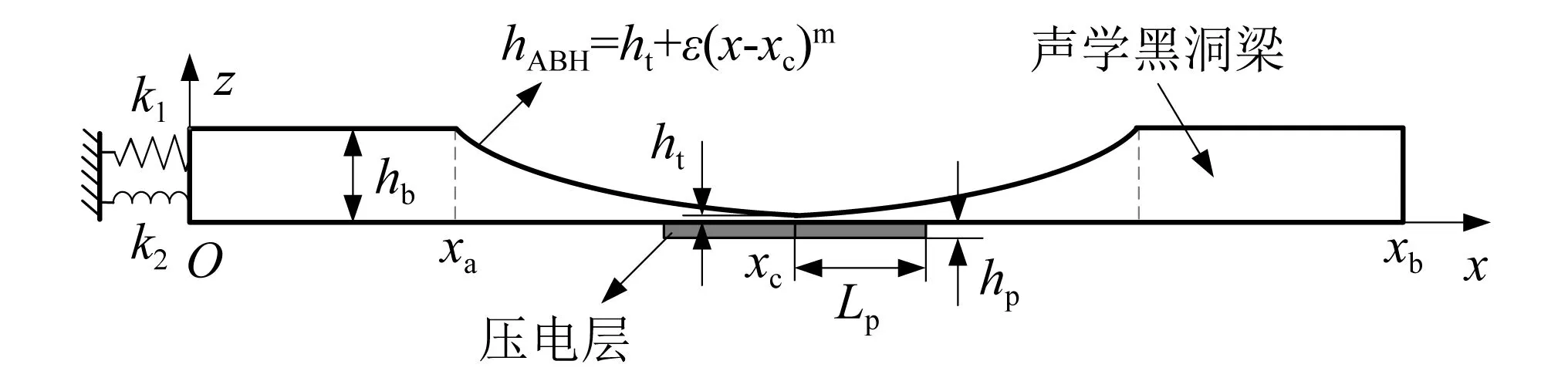
圖1 單胞聲學黑洞結構示意圖Fig.1 Schematic diagram of the structure of a single cell acoustic black hole

基于歐拉-伯努利梁假設，梁結構的位移場可以表示為

(4)

式中：[u,w]為梁上任意位置在x方向和z方向的位移；w(x,t)為梁上中面在不同時刻的撓度。其中，撓度w(x,t)可以表示為與位置有關的形函數φ(x)和與時間有關的權重系數a(t)的疊加形式

(5)

為了準確表示系統的質量及剛度矩陣，需要尋找一個合適的基函數去擬合梁的撓度曲線。而高斯函數由于其無限可導，且便于積分的特點，能夠適應由于黑洞邊緣而急劇變化的彎曲波波數。因此，為了提高擬合精度與計算速度，通過在高斯函數g(x)=exp[-x2/2]中引入平移因子與伸縮因子來擬合形函數φ(x)，表示為[19]

φi=2pi/2exp[-(2pix-qi)2/2],?i=1,…,N

(6)

式中：pi為高斯函數的伸縮因子；qi為平移因子。其中，伸縮因子決定著模型的求解精度與求解速度，取值越大，計算精度則越高，但計算時間也越長。伸縮因子的取值范圍所需要滿足的基本條件是，它的最小值需要與梁在x方向上的尺寸相匹配[20], 因此，伸縮因子的取值范圍則為

pi=ceil(log28/Lunit)

(7)

而平移因子qi決定著質量矩陣與剛度矩陣的維度，其取值范圍由伸縮因子與結構尺寸共同決定，一般為

qi=[-3+floor(-2pixleft),3+ceil(2pixright)]

(8)

式中：Lunit為需要計算的梁的全長，這里針對單胞結構即為單胞的長度；xleft與xright分別為梁的積分上下限，即梁的左右端點坐標；floor(x)與ceil(x)分別為向上取整與向下取整運算。

單胞結構間的連續性條件應該滿足兩單胞在連接處的位移、轉角、彎矩相同，剪切力相反，即表示為

wn(xb,t)=wn+1(0,t)

(9)

(10)

(11)

w?n(xb,t)=-w?n+1(0,t)

(12)

式中，wn(xb,t)，wn+1(0,t)分別為前、后兩個單胞連接處在t時刻的位移，各階導數則依次表示轉角、彎矩與剪切力。

基于能量法，可以建立系統的動能K、勢能U、電能We和外力功Wf方程。系統的動能表示為梁與壓電片動能的集合

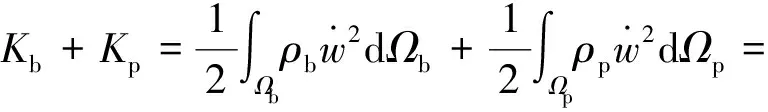
(13)

式中：ρb，ρp分別為梁與壓電片的密度；M為梁與壓電片總的質量矩陣。勢能則分為梁、邊界彈簧與壓電片3個部分，其中梁的勢能為

(14)

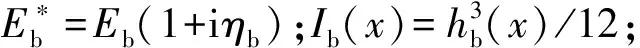
對于壓電片的勢能計算，需要引入壓電材料的本構方程。針對薄梁的線性壓電本構簡化方程[21]為

(15)

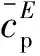
(16)

式中：Kρ為壓電片的剛度矩陣；Θ為機電耦合向量。

在梁的左端加載兩個剛度可調的邊界彈簧，分別為平移彈簧與扭轉彈簧，通過給邊界彈簧賦予不同的剛度條件，來起到模擬多種邊界條件的作用。邊界彈簧的彈性勢能表示為

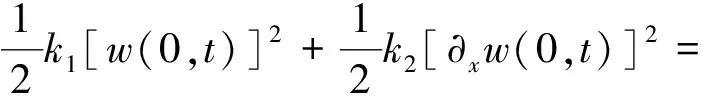
(17)

因此系統的總勢能表示為

(18)

式中，K=Kb+Kp+Kedge為梁、壓電片以及邊界彈簧的總剛度矩陣。壓電片中產生的電能表示為

(19)

式中，Cp為壓電片的電容。系統的外力功可以表示為作用在xf位置上的機械外力f(t)與電壓Vp和電荷q的關系

Wf=f(t)w(xf)+Vpq=aTf+Vpq

(20)

最后，拉格朗日算子可表示為L=K-U+We+Wf，分別將式(13)、式(18)、式(19)、式(20)代入拉格朗日算子可得

(21)

拉格朗日機電耦合方程為

(22)

將式(21)代入式(22)求導計算得到

(23)

(24)

式中，R為能量采集電路中的等效電阻。

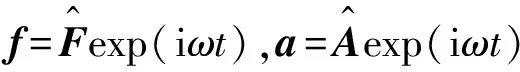
(25)

2 結構參數對能量回收特性的影響

為了便于能量回收功率的計算，將周期聲學黑洞梁的左右邊界均作自由邊界處理，取幅值為1 N的激勵力施加在梁結構的左端徑向方向，并將每一個單胞聲學黑洞的能量回收電路簡化為一個阻值為100 Ω的負載電阻，其結構示意圖如圖2所示。

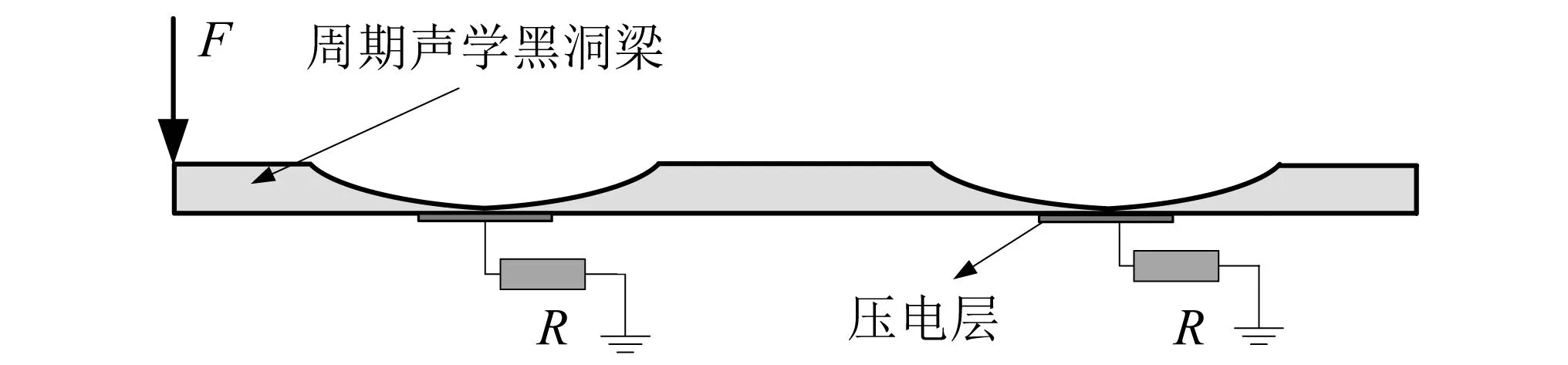
圖2 周期聲學黑洞能量回收示意圖Fig.2 Schematic diagram of energy harvesting of periodic acoustic black hole

結構中梁與壓電層的幾何參數與材料屬性，分別如表1和表2所示。為探究各結構參數對于能量回收的影響，分析不同周期數N、黑洞半徑rabh、冪指數m以及中心截斷ht等情況下結構的穩態響應。其中，將黑洞區域與均勻區域交界點代入黑洞厚度分布函數，即

hb=ht+ε(x-rabh)m

(28)

由式(26)可得

(27)

因此，冪變系數ε作為結構函數中的因變量，隨著黑洞半徑rabh、冪指數m以及中心截斷ht的變化而變化。

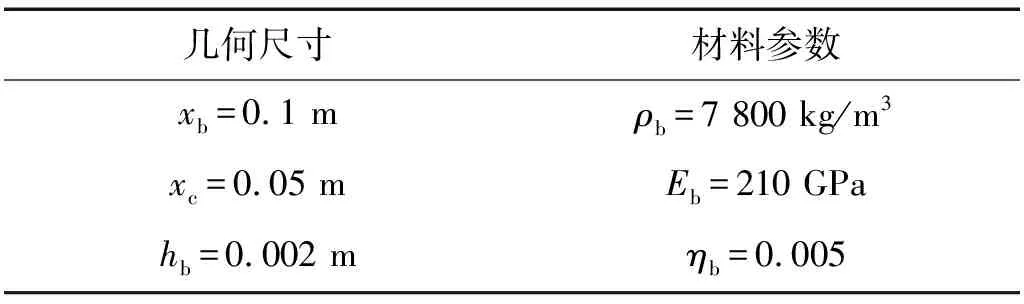
表1 單胞聲學黑洞梁模型參數Tab.1 Parameters of the black hole beam

表2 單胞壓電層模型參數Tab.2 Parameters of piezoelectric layer

2.1 周期數對于能量回收特性的影響

在單胞幾何參數恒定的情況下，通過更改周期數N以研究周期化程度對于壓電能量回收效應的影響。周期數分別為1，5，10，20時聲學黑洞梁的能量回收功率圖，如圖3所示。圖3中，取對數時的參考值為Pref=1×10-2W(其余功率圖也采取相同的對數參考值)。

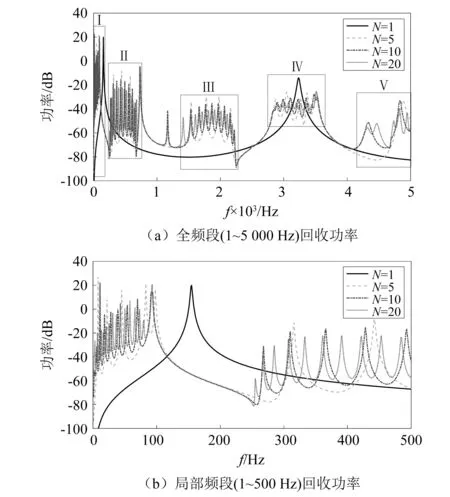
圖3 不同周期數下周期聲學黑洞能量回收功率Fig.3 Energy harvesting power of periodic acoustic black holes with different periods

由圖3可以看出，在1～5 000 Hz的分析頻段內，回收功率峰值密集分布區域集中在如圖所示的Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ這5個頻段內。周期20的聲學黑洞梁回收功率與單胞能帶結構圖的對比，如圖4所示。圖4中，深色頻段即為無限周期預測的結構通帶范圍。由圖4可以看出，回收峰值密集分布的5個頻段對應于結構中的5個結構通帶。之所以在通帶范圍能夠實現更高的回收功率，是因為在通帶范圍之外的禁帶區域內，彎曲波傳遞受阻，結構振動被極大的抑制，因此回收功率從峰值開始劇烈下降；而在通帶頻率范圍以內，波動能量被大量聚集在了這一頻段內，壓電材料隨梁結構劇烈形變，回收功率明顯提升。由圖4可知，在頻段Ⅰ、Ⅲ、Ⅴ內，周期聲學黑洞的回收功率遠高于單一的聲學黑洞結構。而在頻段Ⅳ內，雖然單一聲學黑洞在3 234 Hz左右的回收功率更高，但周期聲學黑洞利用結構通帶，在更寬的頻率范圍內實現了較高的回收功率。由此可見，利用周期性產生的結構通帶，可以將原本聚集在共振頻率周圍的能量分散至通帶頻率范圍內，從而實現振動能量的寬頻回收。

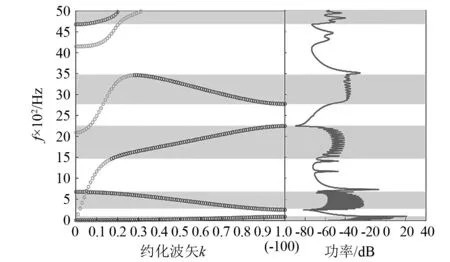
圖4 能帶結構與回收功率對比圖Fig.4 Comparison chart of energy band structure and harvesting power

為了進一步說明周期數對于能量回收效果的影響，定義各個頻段內的峰值間隔Δfi的計算式為

Δfi=(fimax-fimin)/n

(28)

式中：fimin，fimax為i頻段內第一個與最后一個回收峰值所對應的頻率；n為該頻段內的峰值個數。

由于分析頻段的上限設置為5 000 Hz，導致頻段Ⅴ未展示出完整的峰值頻段，因此平均峰值間隔的均值計算只納入前四段峰值頻段，各頻段內平均峰值間隔如表3所示。

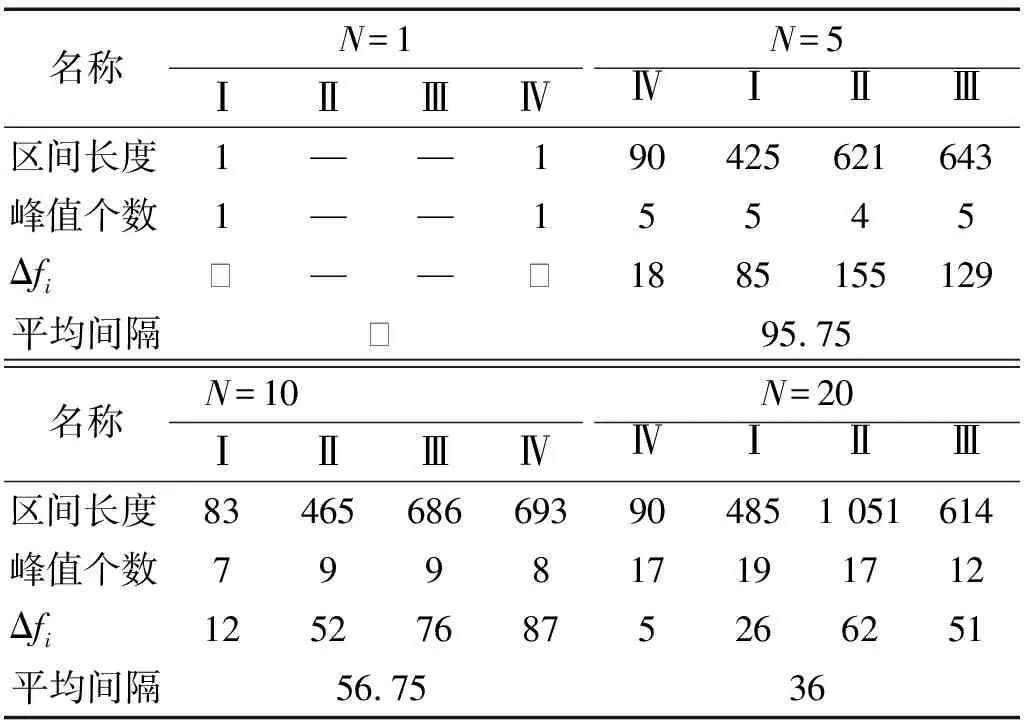
表3 各頻段平均峰值間隔Tab.3 Average peak interval of each frequency band

結合圖3與表3可以看出，當周期數為1時，聲學黑洞結構僅在外界激勵頻率為155 Hz，3 234 Hz時能夠形成回收峰值；隨著結構周期數的增多，在通帶頻率范圍內形成的峰值個數也在增多，且全頻段內的平均峰值間隔也在降低，但當周期數增加為20時，全頻段內的平均峰值間隔僅為36 Hz，低于N=5時的95.75 Hz與N=10時的56.75 Hz。此外，在各通帶范圍內形成的回收功率波峰與波谷的差值，也隨著周期數的增多而降低，也就是說，此時回收功率受外界激勵頻率的影響波動更小，即在實現寬頻能量回收的同時，輸出功率的穩定性也更好。

2.2 冪指數對于能量回收特性的影響

在黑洞半徑以及中心截斷厚度一定的情況下，冪指數決定了聲學黑洞厚度變化的快慢。如圖5所示，冪指數越大，黑洞區域的厚度變化越劇烈，也就是說，在相同坐標系下的同一截面位置，冪指數越大，聲學黑洞梁的厚度越小，即h2>h3>h4。

圖5 變冪指數聲學黑洞結構示意圖Fig.5 Schematic diagram of the structure of acoustic black hole with variable power

圖6為10周期聲學黑洞結構在冪指數分別為2、3、4情況下，各結構的能量回收功率曲線。

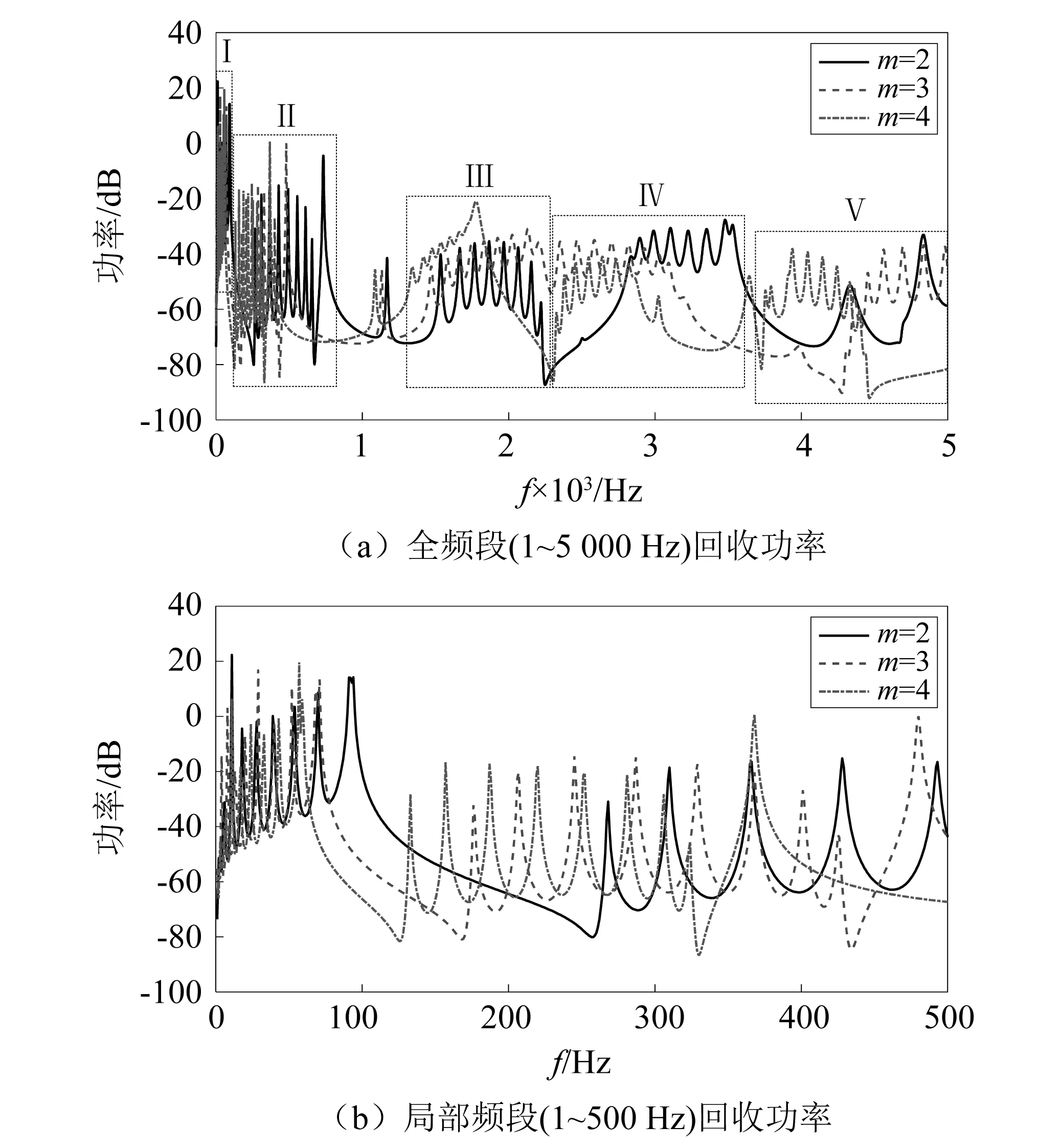
圖6 不同冪指數下周期聲學黑洞能量回收功率Fig.6 Energy harvesting power of periodic acoustic black hole with different power exponent

由圖6各條曲線的頻率分布可以看出，各個峰值密集分布頻段內的峰值個數不會隨著結構的冪指數變化而變化；結合局部頻段的放大圖可以明顯看出，隨著冪指數的增大，各頻段內的峰值間隔明顯縮短，結合峰值個數保持一致的現象，可知各峰值區間的長度隨著冪指數的增大而縮短；此外，各峰值頻段也呈現出明顯的向低頻移動的趨勢。由圖7的能帶結構對比圖，同樣可以看出相同的趨勢，即隨著冪指數的增大，各條結構通帶均發生不同程度的壓縮，并向低頻方向移動。

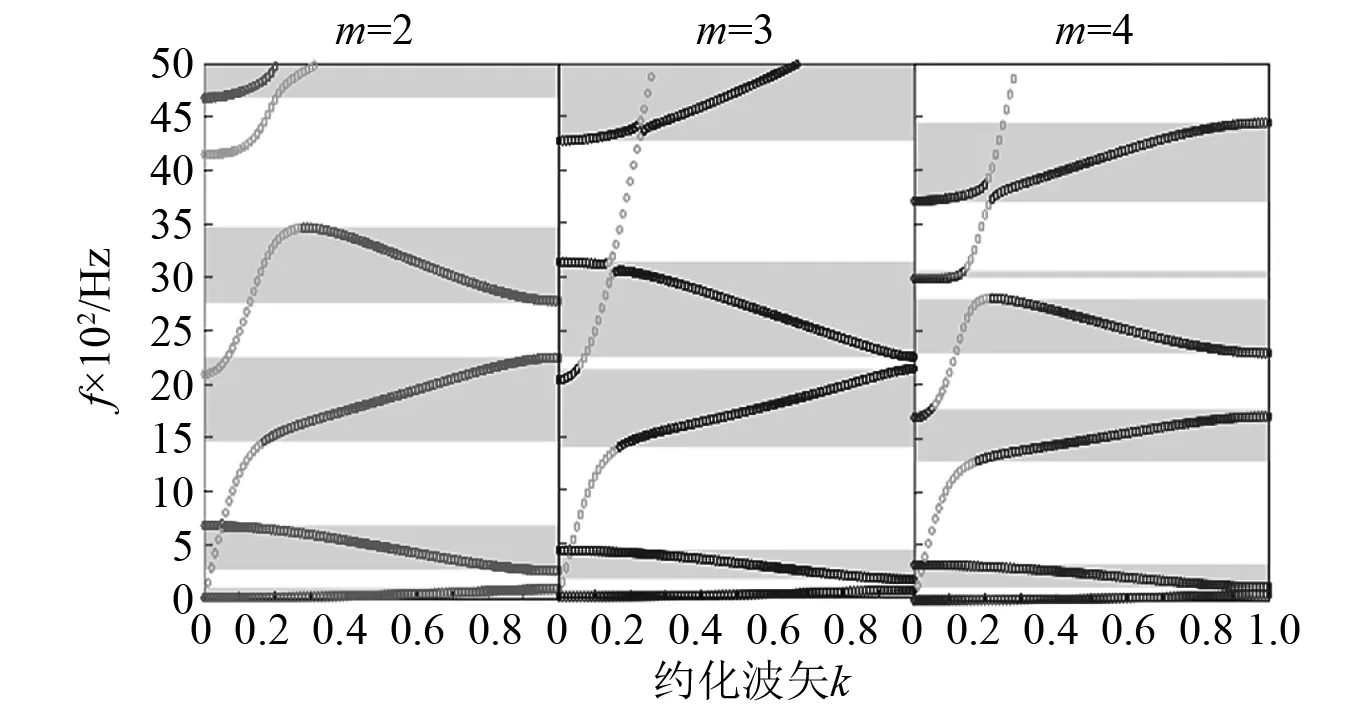
圖7 不同冪指數的周期聲學黑洞結構能帶圖Fig.7 Energy band of periodic acoustic black hole structure under different power exponents

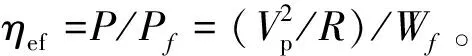
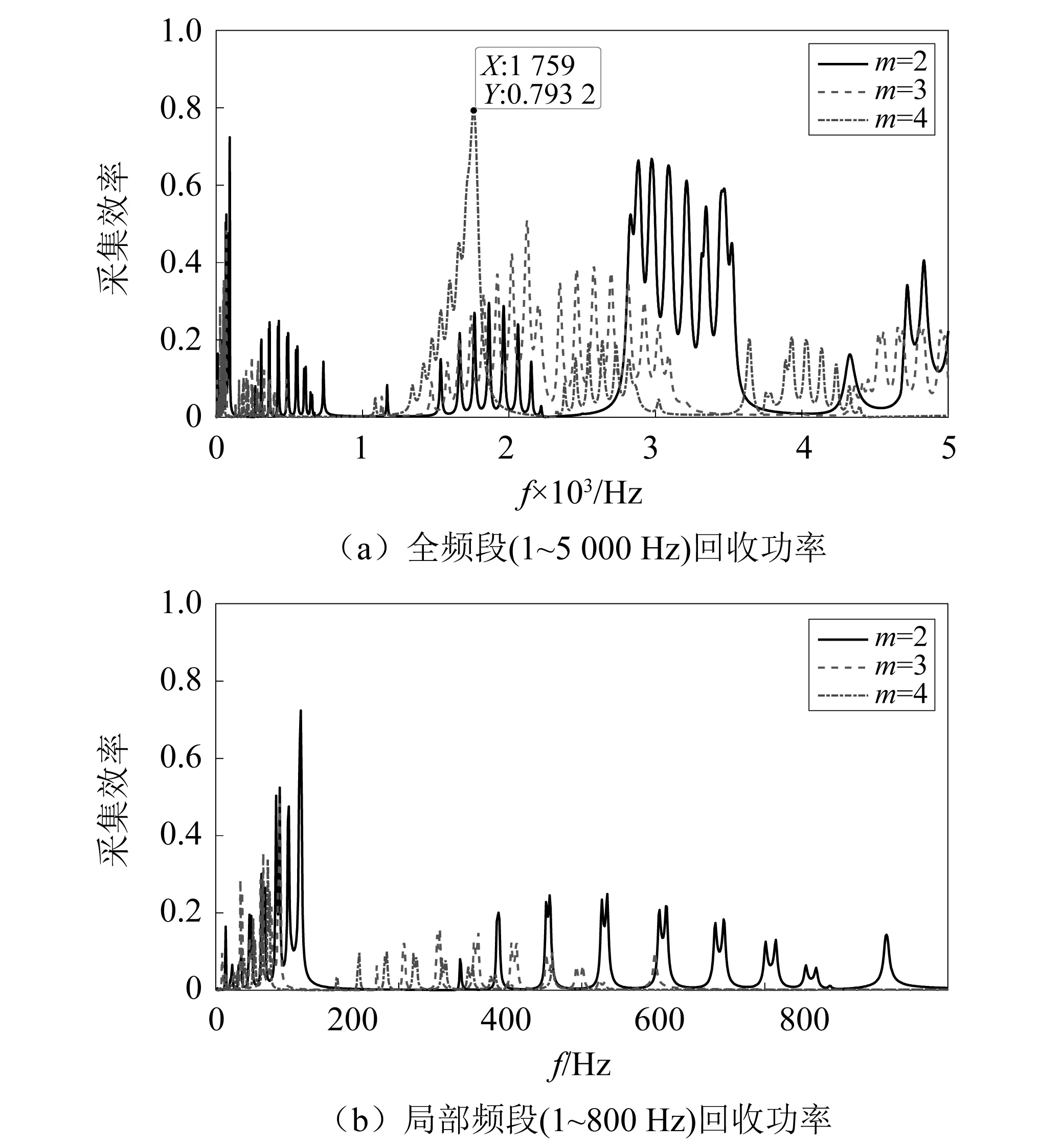
圖8 不同冪指數下周期聲學黑洞能量回收效率Fig.8 Energy harvesting efficiency of periodic acoustic black holes with different power exponent

由能量采集效率圖可知，在第Ⅲ頻段內，能量采集效率呈現出冪指數越大，回收效率越大的規律；在一維梁結構中，彎曲波的波長計算式為

(29)

式中：h為梁的局部厚度；f為外界激勵頻率；E，ρ，μ分別為材料的楊氏模量、密度以及泊松比。

由式(29)可知，在相同激勵頻率下，局部位置厚度越小，彎曲波波長就越小。即冪指數越大的情況下，相同位置截面的厚度就越小，導致彎曲波波長在黑洞區域被更快的壓縮，此時的彎曲波的半波長小于壓電片長度，因而不會在壓電片中產生正負電荷相互抵消的情況，從而獲得更高的能量采集效率。在低頻段內，彎曲波波長較短，無法在壓電片中產生足夠的形變，因此能量采集效率較低；而在高頻段，彎曲波被壓縮至較小的波長，使壓電片中產生正負電荷相互抵消，從而降低了能量采集效率。因此，總的來說，能量采集效率隨著冪指數的增大而減小，但由于半波長截止效應的存在，使在某一頻段內的能量采集效率會隨著冪指數的增大而增大，這一頻段范圍由材料屬性與結構厚度共同決定。

2.3 中心截斷對于能量回收特性的影響

與冪指數對于結構的影響相似，在黑洞半徑恒定的情況下，改變中心截斷厚度，也會改變黑洞區域的厚度變化幅度，中心截斷越小，厚度變化得越快，如圖9所示，在相同坐標軸下同一截面處，中心截斷越大，聲學黑洞梁的厚度越大，即h05>h02>h01。

圖9 變中心截斷聲學黑洞結構示意圖Fig.9 Structure of acoustic black hole with variable truncated center

中心截斷厚度分別為0.1hb，0.2hb以及情況下的10周期聲學黑洞能量回收功率曲線，如圖10所示。不同中心截斷的周期聲學黑洞能帶結構對比圖，如圖11所示。

由圖10和圖11可以看出，當中心截斷為均勻部分厚度一半時，已無明顯的峰值聚集現象，即使此時的通帶范圍極寬，幾乎覆蓋了全頻段，但由于中心截斷過大，導致黑洞中心部分的反射系數較大，此時的聲學黑洞結構已不具備對能量的聚集效應。而當中心截斷由0.1hb加厚到0.2hb時，兩功率曲線變化趨勢相似，幅值差異較小，僅在頻域范圍內，出現了曲線的平移與壓縮。在能帶結構中的表現，就是各通帶范圍加寬，且各頻帶均向高頻移動。由此可得，隨著中心截斷的加厚，回收峰值頻段會向高頻移動，且頻段長度有小幅的拓寬，回收波峰波谷的功率差加大，周期結構的回收功率對于外界激勵頻率的敏感性加大。

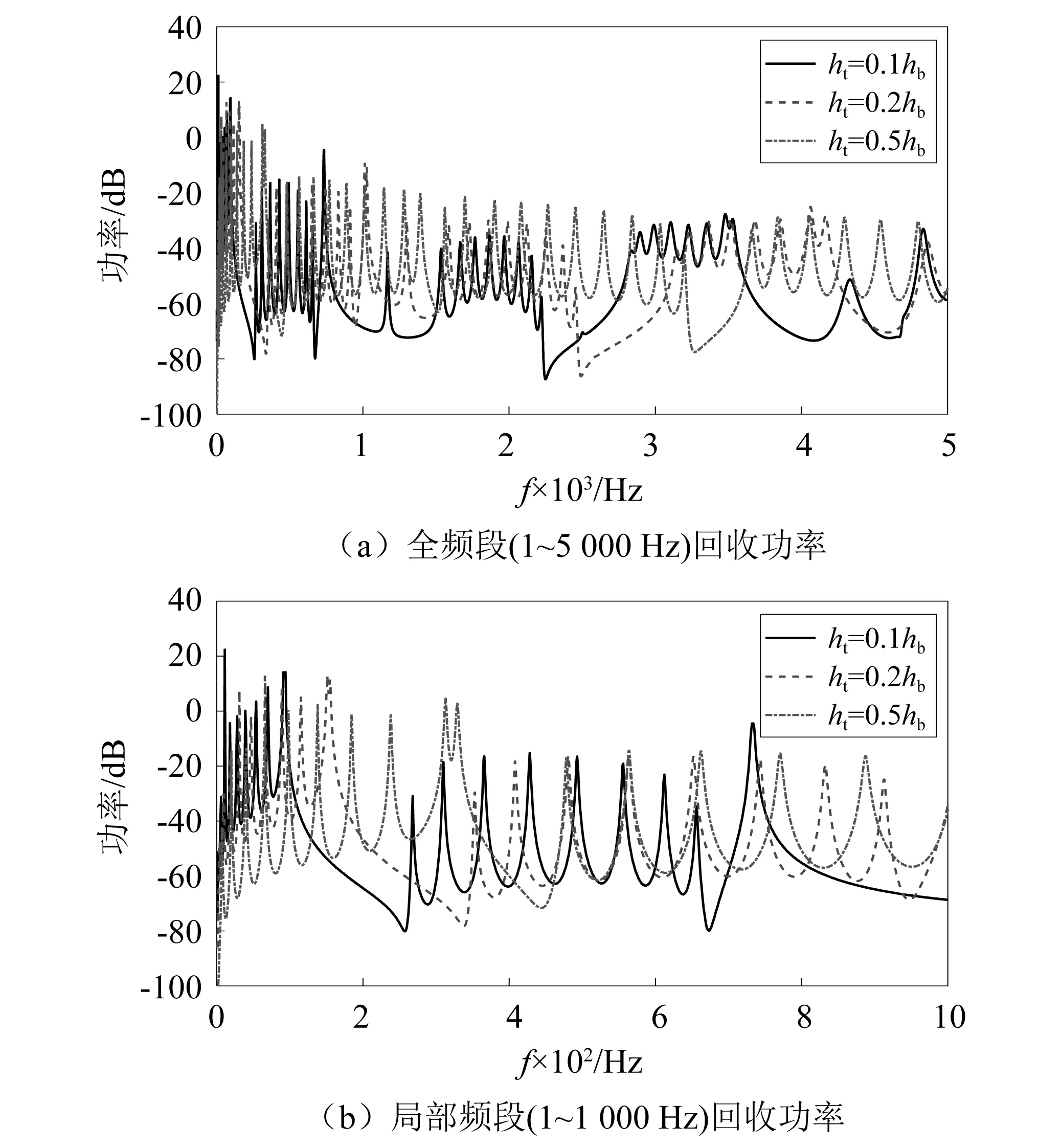
圖10 不同中心截斷下周期聲學黑洞能量回收功率Fig.10 Energy harvesting power of periodic acoustic black holes with different truncation centers

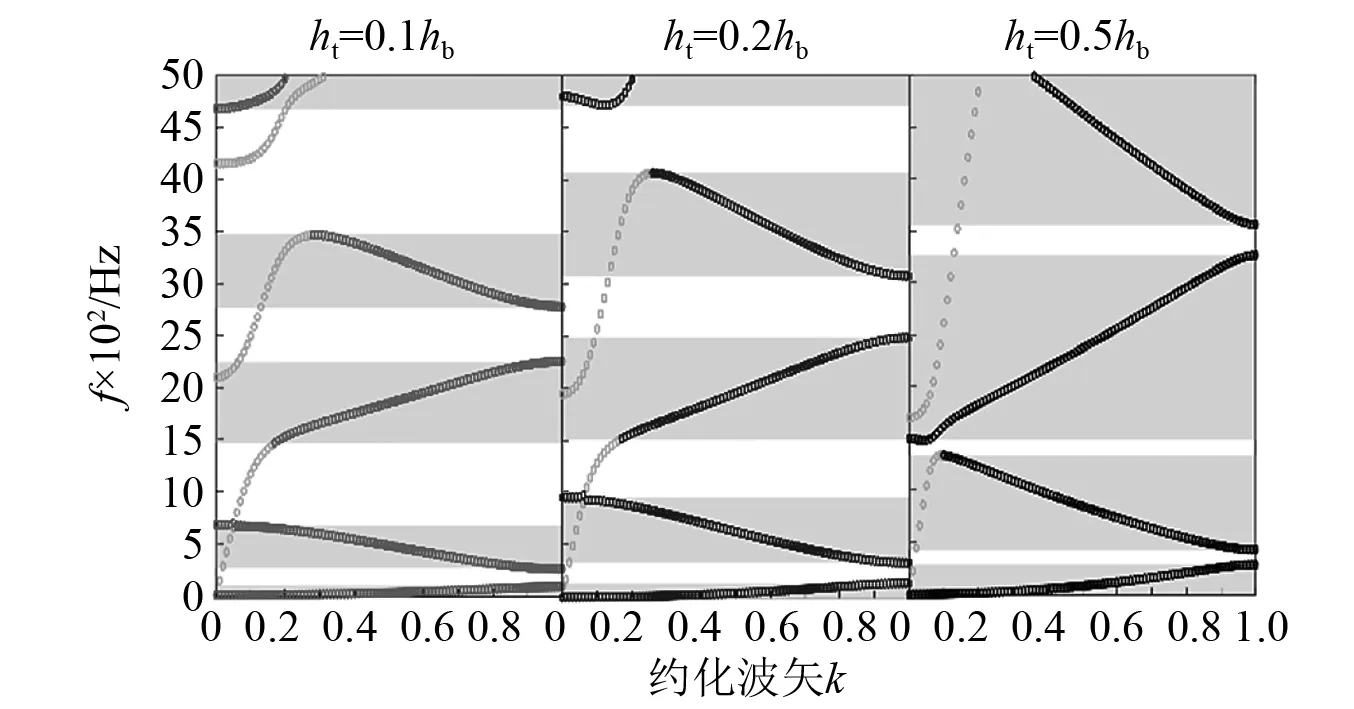
圖11 不同中心截斷的周期聲學黑洞結構能帶圖Fig.11 Energy band of periodic acoustic black hole structure under different truncation centers

2.4 黑洞半徑對于能量回收特性的影響

在中心截斷厚度ht=0.1hb、冪指數m=2以及單胞長度恒定的情況下，取黑洞半徑分別為單胞長度的1/4，1/2，3/4作為分析工況，其厚度變化示意圖如圖12所示。從圖12可以看出，黑洞半徑的變化不僅會直接影響黑洞區域與均勻部分的占比，也間接使黑洞區域的厚度發生變化，黑洞半徑越大，厚度變化越緩慢。

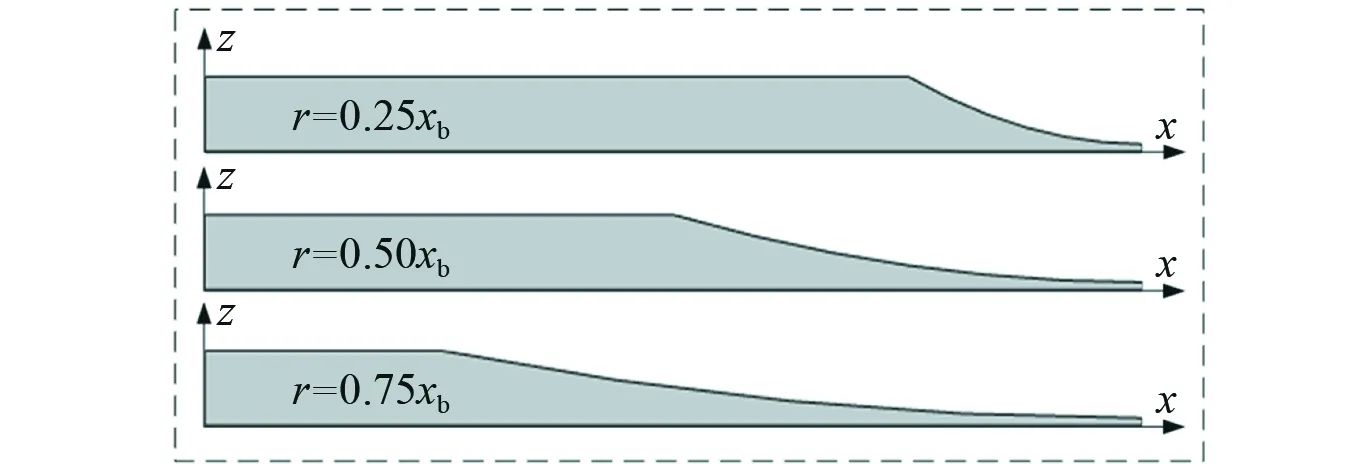
圖12 變黑洞半徑聲學黑洞結構示意圖Fig.12 Schematic diagram of acoustic black hole structure with variable radius

各分析工況下的聲學黑洞結構回收功率圖與能帶結構對比圖，分別如圖13、圖14所示。從計算結果來看，隨著黑洞半徑的增大，在低頻部分的Ⅰ、Ⅱ、Ⅲ峰值頻段以及其對應的能帶范圍，均向低頻移動，頻段長度也發生一定的壓縮。此外，當黑洞占比達單胞長度的3/4時，回收功率曲線在2 000 Hz以后的高頻段內出現了連續分布的回收峰值，且波峰與波谷對應的幅值相對穩定，在較寬的頻率范圍內均高于其余兩種工況。從能帶結構圖中也可以看出在2 000 Hz之后的高頻范圍內出現了兩段覆蓋范圍很寬的結構通帶，也就是說，此時結構在高頻區域能夠展現出更穩定的高效能量回收效果。

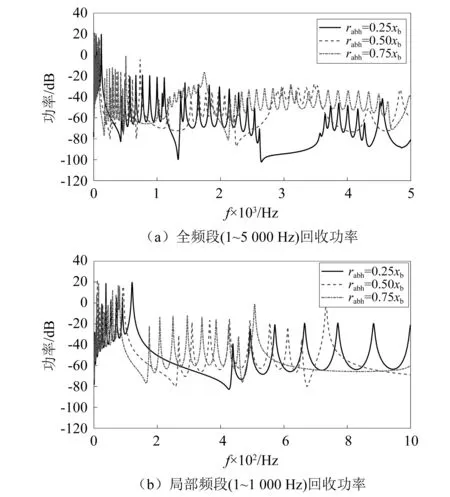
圖13 不同黑洞半徑下周期聲學黑洞能量回收功率Fig.13 Energy harvesting power of periodic acoustic black hole with different radius

表4為計算得到的不同黑洞半徑情況下的能量轉換效率。由表4可知，即使較大的黑洞半徑能夠在高頻段實現輸出功率更高更穩定的能量回收效果，但從全頻段內的能量轉換效率來看，雖然總輸出電能增多，但能量轉換效率仍然有所降低。

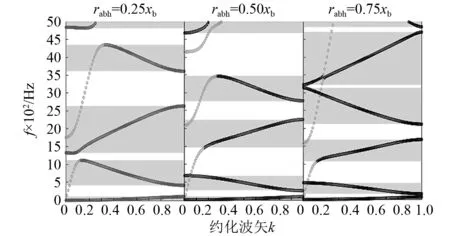
圖14 不同黑洞半徑的周期聲學黑洞結構能帶圖Fig.14 Energy band of periodic acoustic black hole structure under different radius

表4 全頻段內能量轉換效率Tab.4 Energy conversion efficiency in full frequency band

3 試驗驗證

基于周期聲學黑洞結構的壓電能量回收試驗系統的實物圖，如圖15所示。試驗系統由三部分組成，分別為激勵單元、信號采集單元與數據處理單元。由信號發生器產生固定頻率的正弦信號，經過功率放大器調節增益之后，傳遞到激振器中，驅動激振器產生諧振力并作用在試驗梁上。試驗梁與激振器的連接方式如圖16所示，而梁的另一端則采用懸掛系統模擬自由邊界條件。當激振器發出的正弦激勵作用在試驗梁上時，會在結構中產生彈性波，進而在粘貼在梁上壓電片中產生電勢。通過LMS采集卡測量連接在壓電片上的負載電阻的電壓，就可以得到系統在單一頻率作用下的穩態回收功率。為了滿足振動試驗所需的結構強度，聲學黑洞梁與均勻梁的材料均選為鋁合金，其結構如圖17所示，梁全長為1 m，寬度為20 mm，高度為10 mm。對于聲學黑洞梁的結構單胞，其單胞長度為200 mm，黑洞半徑為100 mm，非均勻部分的厚度與位置的關系式滿足h(x)=1.406 3×10-5x2+1,(0≤x≤80)，式中x代表到單胞結構中心的距離。壓電陶瓷片的材料為PZT-5，結構尺寸為60 mm×20 mm×0.2 mm，在聲學黑洞梁上的各個單胞結構中心均粘貼有一塊壓電陶瓷片，并在均勻梁的相同位置上布置了同等數量的壓電材料。

在保證功率放大器增益恒定，且負載電阻均為100 Ω的情況下，在1～1 000 Hz的頻段范圍內，以25 Hz為步長調整激勵頻率，分別測量每一塊壓電片在同一激勵頻率下的穩態輸出電壓，并計算其輸出功率，最后將各壓電片的穩態輸出功率線性相加，即得到總的輸出功率。兩根試驗梁在1 000 Hz以內的回收功率對比圖，如圖18所示。

圖15 壓電能量回收試驗系統圖Fig.15 Piezoelectric energy harvesting experimental system diagram

圖16 試驗梁與激振器連接圖Fig.16 Connection diagram of test beam and vibration exciter

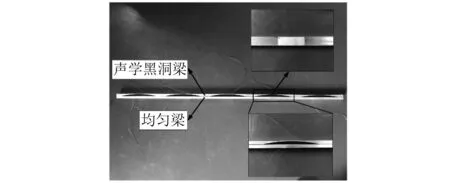
圖17 聲學黑洞梁與均勻梁結構對比圖Fig.17 Comparison of acoustic black hole beam and uniform beam structure

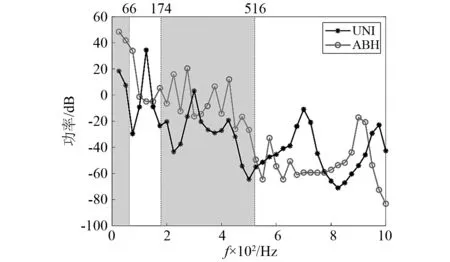
圖18 聲學黑洞梁與均勻梁回收功率對比圖Fig.18 Comparison of harvesting power between acoustic black hole beam and uniform beam

由圖18可以看出，在1 000 Hz以內，通過無限周期理論推導出的試驗梁結構通帶在0～66 Hz，174～516 Hz這兩個頻率范圍。而在第一個通帶內，由于采樣頻率間隔較大，所以周期聲學黑洞梁未顯示出足夠的回收峰值，但與均勻梁相比，其回收功率也優于均勻梁。這是因為在低頻部分，聲學黑洞的振動幅度較大，使壓電片產生了較大的形變，因此其輸出功率大于均勻梁；在第二個通帶范圍內，就可以明顯看出，周期聲學黑洞在結構通帶頻率范圍內，回收功率峰值相較于均勻梁更多，且平均回收功率也高于均勻梁，在更寬的頻率范圍內實現了能量的高功率回收。將試驗結果與計算結果(見圖3)進行對比，周期聲學黑洞利用結構通帶實現寬頻能量回收的效果基本保持一致。

4 結 論

本文基于高斯展開法建立了耦合壓電材料的周期聲學黑洞梁能量回收半解析模型，分析了周期數、冪變指數、中心截斷厚度以及黑洞半徑對于能量回收特性的影響，主要結論如下：

(1) 周期聲學黑洞能夠通過形成結構通帶，來有效實現能量的寬頻回收。隨著聲學黑洞的周期數增多，輸出功率的峰值個數增多，波峰與波谷的功率差降低，此時結構的輸出功率受外界激勵頻率的影響波動更小。

(2) 冪指數不會改變峰值分布頻段內的峰值個數，但隨著冪指數的增大，各段結構通帶均發生不同程度的壓縮，并向低頻方向移動。能量采集效率由于半波長截止效應在部分頻段內隨著指數的增大而增大，在其他頻段內均呈現隨著冪指數的增大而減小趨勢。

(3) 在聲學黑洞半徑一定的條件下，隨著中心截斷的加厚，回收峰值頻段會向高頻移動，且頻段長度有小幅的拓寬，回收波峰波谷的功率差加大，周期結構的回收功率對于外界激勵頻率的敏感性加大。

(4) 低頻部分的能帶結構會隨著黑洞半徑的增大而向低頻移動，頻段長度也發生一定的壓縮；更大的黑洞半徑能夠在高頻段實現更穩定、輸出功率更高的能量回收效果，但全頻段內的能量轉換效率會隨著黑洞半徑的增大而減小。

本文基于所建立的耦合壓電材料聲學黑洞梁能量回收模型，可以研究聲學黑洞各結構參數對于能量回收特性的影響機制，能夠為多周期聲學黑洞的振動能量回收優化設計提供參考依據。