服務員休假的生產服務庫存模型的穩態分析及最優生產策略

徐 浩, 岳德權

(燕山大學理學院，秦皇島 066004)

0 引言

隨著生產庫存理論研究的不斷深入，對于現實生活中一些復雜的服務現象需要我們建立更加完善的模型。將服務員休假和生產庫存系統相結合，有效地分析系統中無庫存情況下的服務員休假的生產庫存模型，通過求解穩態概率研究服務員休假對庫存管理的影響。

在排隊庫存系統文獻中，已有許多學者考慮了服務員(服務臺)的休假對庫存管理的影響問題。Daniel 和Ramanarayanan[1]研究了(s,S)策略的庫存系統，其中服務臺只有在庫存變為零時開始休假。他們假設在缺貨期間或服務臺休息期間到達的需求將丟失。假設需求、提前期和休假時間遵循一般分布。通過使用更新和卷積技術，他們獲得了穩態轉移概率的表達式。Narayanan 等[2]考慮了具有隨機正服務時間的庫存系統。客戶按照Markovian 到達過程到達，服務時間和休假時間具有位相型分布。只要系統中沒有客戶等待或庫存水平為零，服務臺就會休假。他們利用了水平相依的擬生滅過程對系統進行了穩態分析。Sivakumar[3]分析了一個具有馬爾可夫需求的連續盤點庫存系統。顧客到達服從Poisson 過程，服務時間服從指數分布。只有當系統庫存為零時，服務員立即進行休假。休假結束后，若庫存為零則繼續休假，且休假期間到達的顧客進入無限空間的等待池。在穩態情況下獲得了庫存水平和系統中顧客數的聯合分布以及系統的一些穩態性能指標。Padmavathi 等[4]分析了單重休假和多重休假的排隊庫存模型。只有當庫存為零時，服務臺開始休假，若休假結束時，庫存已經到達，則服務臺結束休假，否則繼續休假。并假設Poisson 到達，指數服務時間和指數前置時間。利用矩陣幾何解法得到了兩個休假模型下的Markov 鏈的平穩分布以及產品庫存水平和服務隊列長度的聯合概率分布。Koroliuk 等[5]討論了一個帶有易腐特性，不耐煩客戶和服務員休假的排隊庫存系統，在假設Poisson 到達，指數服務時間和指數前置時間的條件下，得到最佳庫存管理策略。

Krishnamoorthy 和Narayanan[6]研究了基于(s,S)策略的帶有隨機服務時間的生產服務庫存系統，建立了系統隊長、庫存水平、生產狀態的三維馬爾可夫鏈，分析了系統穩態下的各項性能指標。王童毅等[7]考慮了兩種不同優先級顧客的不耐煩行為和服務能力可調節的情況。建立了系統的Markov 模型，給出了系統的穩態分布，獲得了系統的重要性能指標與利潤函數，同時設計搜索算法獲得了系統的最優庫存水平與最優服務能力控制閾值，并得出基本庫存水平，額外服務能力，顧客到達速率對系統凈利潤的影響關系。王曉燕等[8]研究了具有不耐煩顧客的生產服務系統的建模與優化問題。生產設施生產兩種產品，服務臺基于兩類顧客的不同需求提供不同的服務，其每類顧客需要的產品一一對應。通過建立生產兩類產品的生產服務系統Markov 模型，給出了系統穩態分布的求解方法，以及系統的重要性能指標。Baek 和Moon[9]研究了M/M/1 生產庫存系統。客戶根據泊松過程到達系統，并且單個服務器為客戶服務。考慮外部訂貨和內部生產兩種補貨策略。最后得到系統的穩態分布。

目前，雖然在生產服務庫存上的關注和研究較多，但在生產庫存系統中考慮休假的文獻則相對較少。Viswanath 和Krishnamoorthy[10]研究了具有服務員休假的生產服務庫存系統。當庫存為零時或者系統無顧客時，服務臺開始休假。假設每個產品的生產時間遵循馬爾可夫生產過程，并且客戶到達過程遵循馬爾可夫到達過程。他們求出了系統的穩態分布和穩態性能指標。Yue 和Qin[11]研究了具有服務時間和生產假期的生產庫存系統。一旦庫存水平變為零，生產設備開始休假，假設所有到達的客戶在庫存為零時丟失。根據擬生滅過程理論得到了系統穩態平衡條件，最后給出了一些數值結果。

服務員休假在網購系統方面有明顯的應用背景。例如在網購環境下，網購平臺提供“加購物車–下單–付款”的流程則是服務員向顧客提供服務的過程，網購平臺可視為服務員。以網購某一物品為背景，在庫存非零時，其網絡平臺向顧客提供服務的過程是一直存在的，即服務員一直在工作。當在重大節日或網購節日，如“雙十一”等，由于下單量大，導致庫存減少到零，此時網購平臺會顯示“缺貨中，補貨申請”，即網購平臺無法向顧客提供“加購物車–下單–付款”的流程，也就是說，此時的網絡平臺對于這類物品是處于休假狀態，至補貨到達才開始工作。

本文基于上述背景考慮了服務員休假策略，但卻與文獻[10–11]有所不同。文獻[10]假定庫存為零或系統中沒有顧客時服務員開始休假，而文獻[11]假定庫存為零時生產設備休假，沒有考慮服務員休假的問題。本文假定服務員在庫存為零時開始休假，系統沒有顧客時如果庫存非零，服務員不休假。第1 節給出了模型的描述和假設。第2 節進行了穩態分析，得到了系統的穩態平衡條件和穩態概率分布。第3 節給出系統性能指標和費用函數的計算公式，并通過數值算例分析了系統參數對性能指標，最優策略及最優費用的影響。第4 節給出了本文的結論。

1 模型描述

本文考慮具有(s,S)生產策略的服務員休假的M/M/1 生產服務庫存模型，模型描述如下。

顧客到達服從參數為λ的泊松過程，顧客到達系統后形成一個隊列，且每一個顧客只有一個產品需求。系統只有一個服務員，其服務時間服從參數為μ的指數分布，服務規則為FCFS。

此系統采用的是(s,S)生產策略，即當系統的庫存水平下降到s時，生產設備立即啟動，并且每次只能生產一個產品，產品生產后立即進入倉庫，直到庫存水平達到最大值S時，才停止生產，其生產時間服從參數為η的指數分布。

系統中只有一個服務員，當系統庫存為零時，服務員開始休假。當假期結束時，若系統中有庫存，則服務員立即進入忙期，否則，若休假結束時系統中無庫存，服務員繼續休假。休假時間服從參數為θ的指數分布。若系統中的庫存非零，服務員不休假。服務員休假期間到達的顧客將被拒絕，不能進入隊列。假設需求到達過程，服務過程和生產過程是相互獨立的。

2 系統穩態分析

在本節中，我們首先使用擬生滅過程(QBD)推導出上一節中描述的系統的穩態條件。然后，我們推導出系統穩態分布并計算系統的一些重要的性能指標。

2.1 狀態過程

定義系統的狀態過程為ψ={(N(t),C(t),I(t),J(t));t ≥0}，其中N(t)表示t時刻系統中的顧客數；C(t)表示t時刻的庫存水平；I(t)表示t時刻服務員的休假狀態，其中I(t) = 0 表示服務員休假，I(t) = 1 表示服務員在崗(不休假)；J(t)表示t時刻生產設備的工作狀態，其中J(t)=1 表示生產設備正在生產，J(t)=0 表示生產設備未生產。

過程ψ={(N(t),C(t),I(t),J(t));t ≥0}的狀態空間為

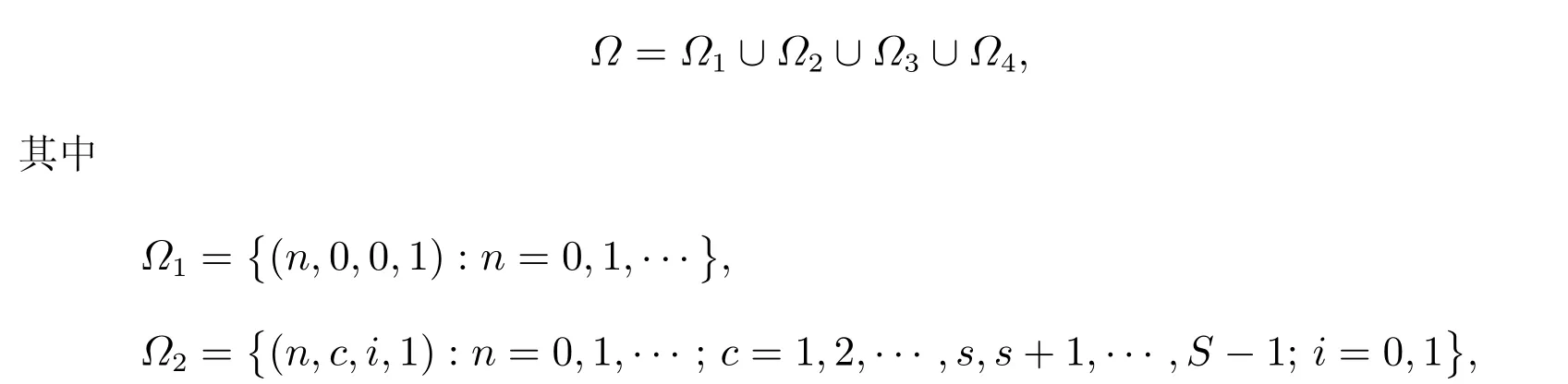
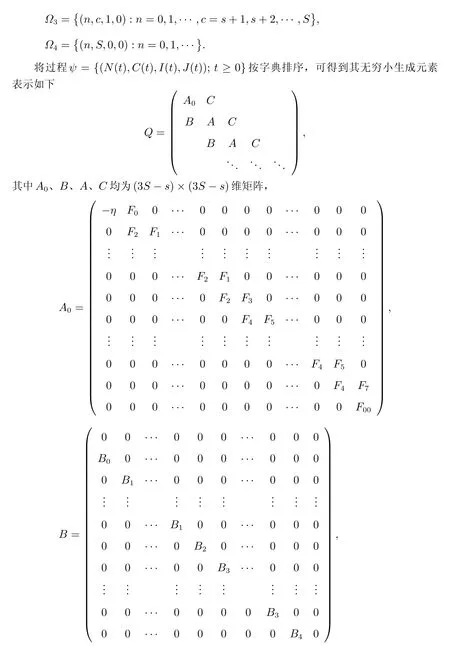
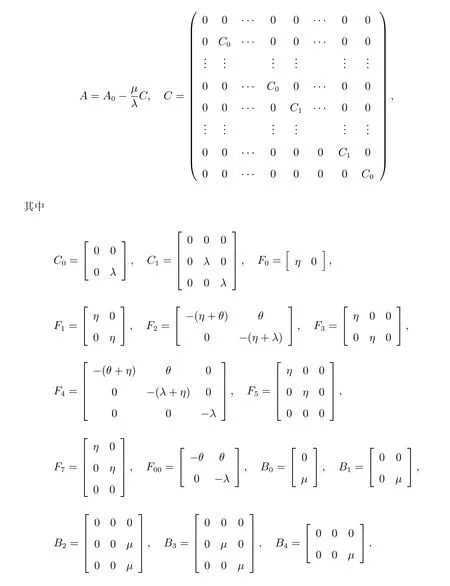
2.2 系統穩態平衡條件

由Q矩陣結構可知過程ψ={(N(t),C(t),I(t),J(t));t ≥0}是擬生滅過程。令M=C+B+A，則有

其中ζ表示服務員處于工作狀態的概率之和，顯然ζ ?= 0。于是，系統穩態分布存在當且僅當λ<μ時成立。

2.3 系統穩態概率

首先考慮服務時間為零的情況，其中定義系統的狀態過程為?ψ={(C(t),I(t),J(t));t≥0}，其中C(t)、I(t)、J(t)的定義同2.1 節。

過程?ψ={(C(t),I(t),J(t));t ≥0}的狀態空間為

其中Pn是(3S ?s)維行向量。

定理1 如果λ<μ，過程{X(t), t ≥0}的穩態概率為

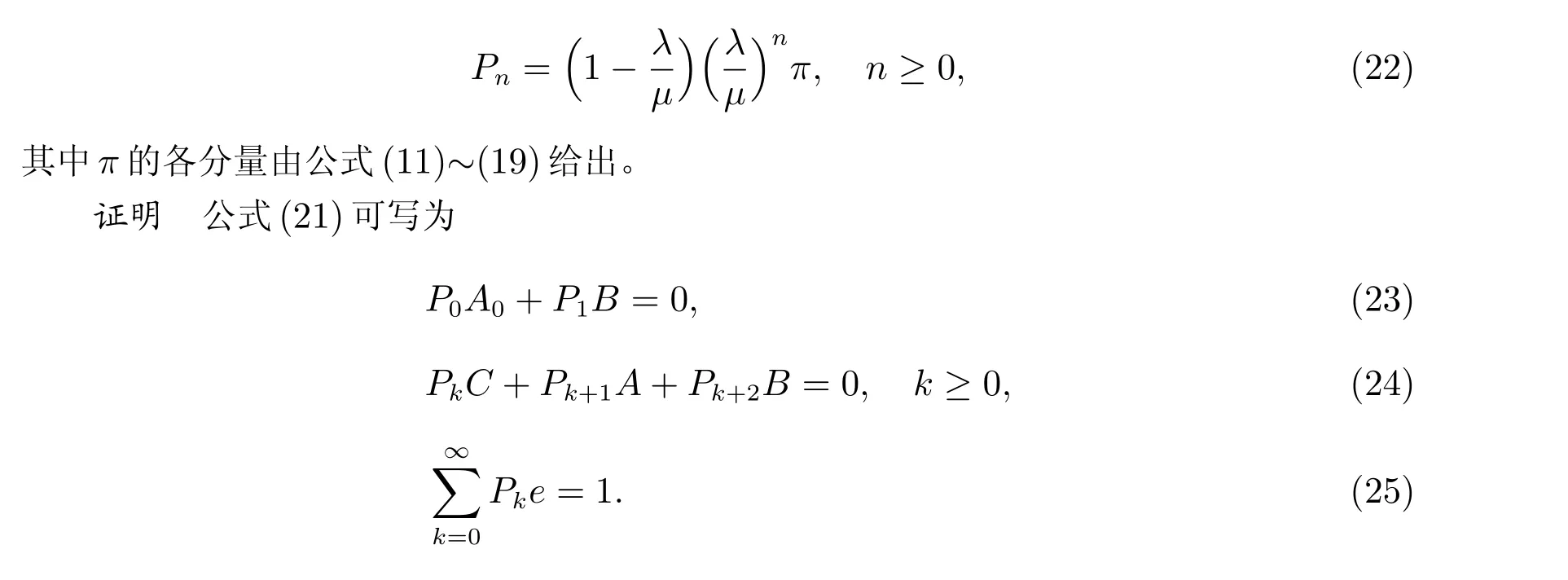
3 系統穩態指標及費用分析

3.1 穩態指標

根據上述穩態概率向量的表達式，易求得系統穩態性能指標，具體如下所示。

1) 平均隊長

上述公式中的π(S,0,0)由公式(19)給出，?由公式(20)給出。

3.2 參數對性能指標的影響

1) 固定η=3, θ=2, s=5, S=45，考慮到達率λ對某些性能指標的影響。

由表1 可知，當到達率λ增大時，生產設備的平均生產率Erp，平均顧客損失率Eloss，服務員平均休假率Evac，生產設備生產時的系統平均庫存Eon，平均生產啟動率Epon都隨之增大。不生產時平均庫存Eoff和總平均庫存Einv在減小。

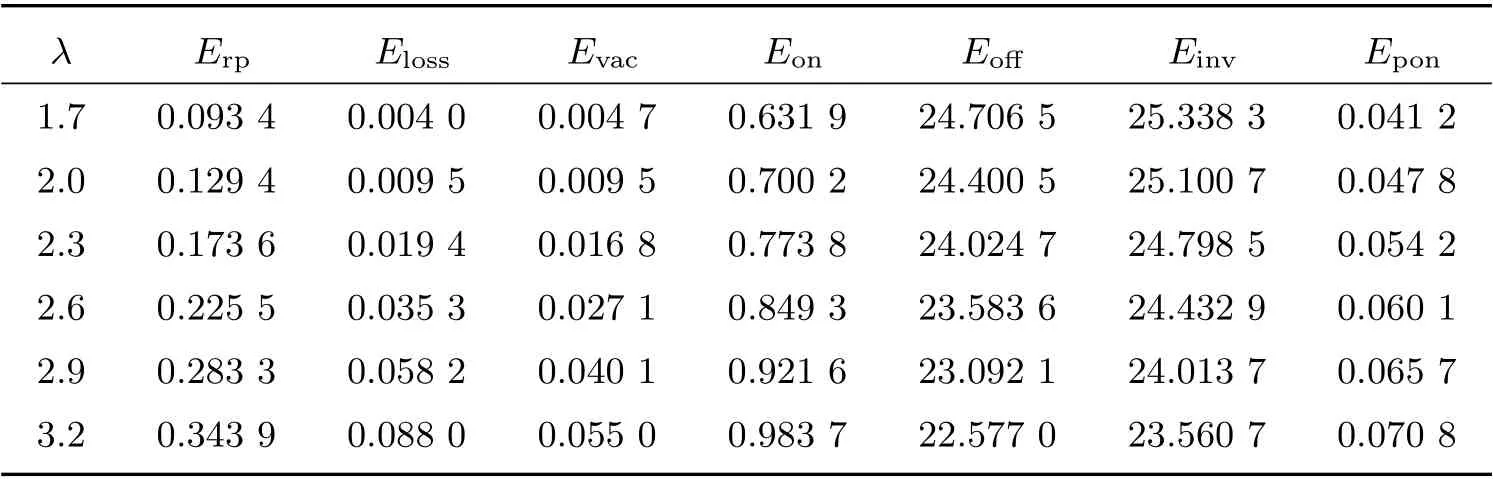
表1 參數λ 的敏感性分析

2) 固定λ=2.7, θ=2, s=5, S=45，考慮生產率η對某些性能指標的影響。

由表2 可知，當生產率η增大時，生產設備的平均生產率Erp，生產設備生產時的系統平均庫存Eon，平均生產啟動率Epon，不生產時平均庫存Eoff和總平均庫存Einv都隨之增大。平均顧客損失率Eloss和服務員平均休假率Evac在減小。

表2 參數η 的敏感性分析

3) 固定λ=2.7, η=3, s=5, S=45，考慮休假率θ對某些性能指標的影響。

由表3 可知，當休假率θ增大時，生產設備的平均生產率Erp和服務員平均休假率Evac都隨之增大。平均顧客損失率Eloss，生產設備生產時的系統平均庫存Eon，平均生產啟動率Epon，不生產時平均庫存Eoff和總平均庫存Einv在減小。

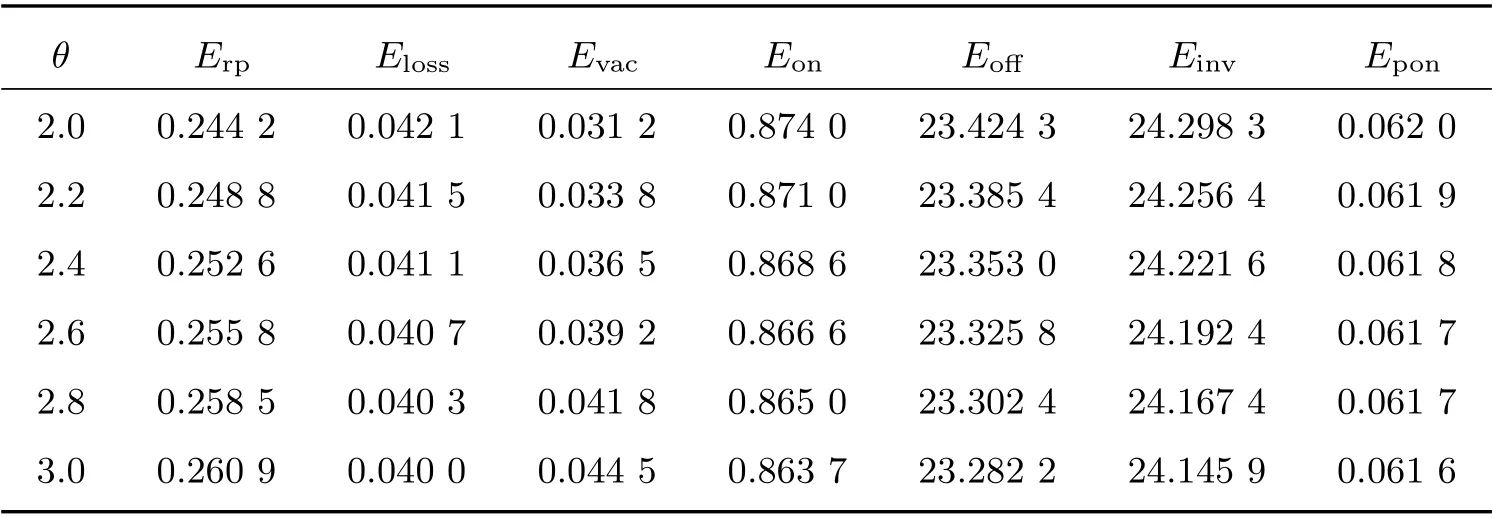
表3 參數θ 的敏感性分析

3.3 費用分析

假設該庫存系統的費用主要由服務費用、庫存保管費用、生產費用、系統的顧客損失費用組成。令單位時間服務費用為Cs，單位時間單位庫存的保管費用為Cinv，單位時間生產費用為Crp，單位時間顧客損失費用為Closs，生產啟動費用Cpon，則系統費用函數為

本文引用王小平和曹立明[13]提出遺傳算法(GA)對該庫存系統的費用函數進行最優求解。遺傳算法采用概率化的尋優方法，不需要確定的規則就能自動獲取和指導優化的搜索空間，自適應地調整搜索方向，因此大大加快了算法的收斂速度。

具體的算法步驟如下：

步驟1 初始化染色體，在可行性區域內隨機生成含有M個體的初始群體；

步驟2 對決策變量進行整數約束，計算評價M個初始群體的適應度；

步驟3 進行個體交叉操作，進而判斷個體的有效性。有效，則保留；無效，則進行隨機位置交叉，直至生成有效的新的種群；

步驟4 進行個體變異操作，再次判斷個體的有效性。有效，則保留；無效，則進行隨機位置變異，直至生成有效的新的種群；

步驟5 對染色體個體進行選擇操作；

步驟6 評價新群體的適應度，找到本代最好染色體，再與上一代進化最好染色體進行比較，記錄每一代進化中做好的適應度和平均適應度；

步驟7 終止條件判斷，如果當前選擇滿足終止條件則停止并輸出當前選擇為最優個體，否則轉到步驟3。

現在，我們研究參數λ、η、θ、μ對最優策略(s?,S?)和最優費用函數C(s?,S?)的影響。數值結果由表4 至表7 給出。Cs=2, Cinv=1, Crp=20, Closs=50, Cpon=2。

表4 給出了參數λ取不同的值時，系統的最優控制策略和一些性能指標的取值變化，其中參數μ= 3.5, θ= 0.8, η= 3.5。由表4 可知，隨著到達率λ的增大，其最小庫存量在逐步減小，最大庫存量在逐步增大，最優費用也在逐漸增大。

表4 參數λ 對最優策略和最優費用的影響

表5 給出了參數η取不同的值時，系統的最優控制策略和一些性能指標的取值變化，其中參數μ= 3.5, θ= 0.8, λ= 1.9。由表5 可知，隨著生產率η的增大，其最小庫存量在逐步增大，最大庫存量在逐步降低，最優費用也在逐漸降低。

表5 參數η 對最優策略和最優費用的影響

表6 給出了參數μ取不同的值時，系統的最優控制策略和一些性能指標的取值變化，其中參數λ= 1.9, η= 3.5, θ= 0.8。由表6 可知，隨著服務率μ的增大，其最小庫存量無顯著變化，最大庫存量也無顯著變化，而最優費用在逐漸降低。

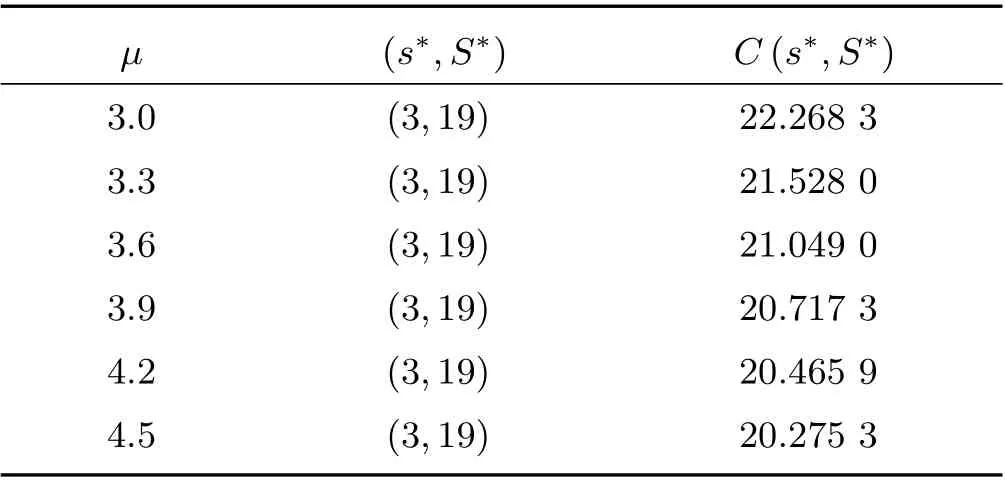
表6 參數μ對最優策略和最優費用的影響

表7 給出了參數θ取不同的值時，系統的最優控制策略和一些性能指標的取值變化，其中參數λ= 1.9, η= 3.5, μ= 3.5。由表7 可知，隨著休假率θ的增大，其最小庫存量逐漸降低，最大庫存量也逐漸降低，而最優費用在逐漸降低。

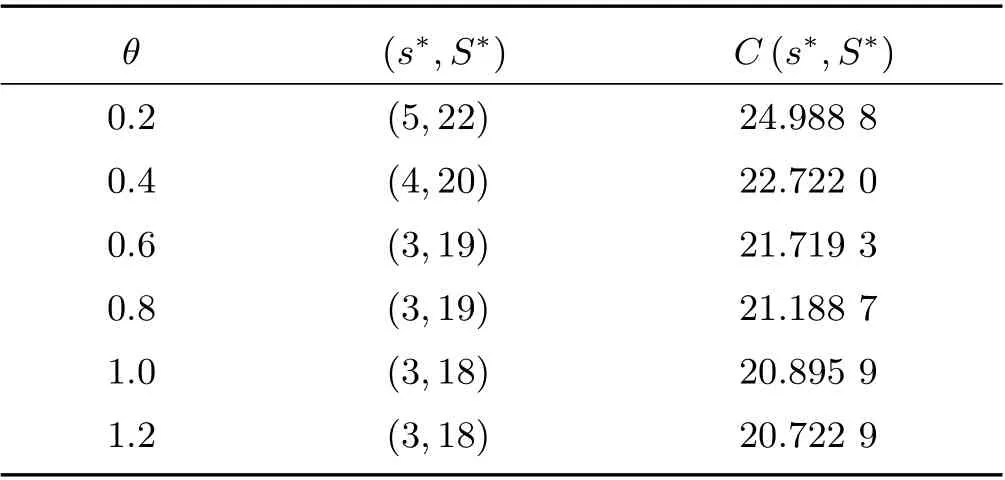
表7 參數θ 對最優策略和最優費用的影響

4 結論

本文研究了庫存為零時服務員休假的M/M/1 生產服務庫存系統，其中生產設施采用(s,S)策略。通過求解矩陣方程獲得了系統隊長和庫存水平的聯合分布，證明了系統的穩態概率分布具有乘積形式解。我們基于一些性能指標構建了費用函數。通過數值實驗考察了一些參數對于性能指標和費用函數的影響。