一種求解一維理想磁流體方程組的保正拉氏方法

鄒世俊, 蔚喜軍, 戴自換

(1. 中國工程物理研究院研究生院，北京 100088; 2. 北京應用物理與計算數學研究所，北京 100088)

0 引言

可壓縮磁流體方程組(MHD)在天體物理、可控熱核聚變、金屬冶煉等眾多科研領域中扮演著重要的角色。此方程組是將氣體動力學方程組與Maxwell 方程組結合起來，廣泛的應用于描述導電流體在磁場中的動力學現象。當忽略黏性，電阻及相對論效應時，上述方程轉化為理想可壓縮磁流體方程組。這組方程組十分復雜以至于很難對其進行數學分析和精確求解，因此，對于理想磁流體方程組設計精確魯棒的數值方法有著十分重要的意義。理想磁流體方程組可以被寫為如下形式

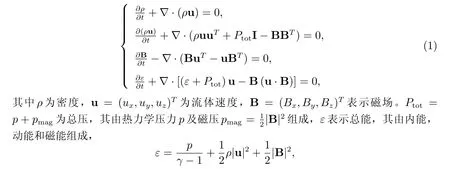
在物理上，上述系統所描述的物理現象中，密度ρ和熱力學壓力p總是非負的。但是，一個逼近上述系統的數值格式所得到的近似解并不能總是保持這種正性，這會引起系統失去雙曲性并導致數值不穩定。為了解決這一問題，許多研究者提出了不同的數值技巧。然而，絕大多數此類方法都是在歐拉框架下提出的，即網格在空間中是固定的。在流體力學的數值模擬中，有另一種框架也被經常使用，這就是拉格朗日框架。在拉氏框架下，計算網格隨流體運動。因此，拉氏方法更加適合處理多介質及自由界面問題。但是，在計算流體力學中保正拉氏格式很少被研究，更不用說是針對于MHD 系統設計的方法了。Bezard 和Desp′res[3]針對一維拉氏MHD 方程組設計了一種數值格式，這一格式滿足熵不等式并在適當的CFL 條件下滿足保正性質。Gallice[6]運用簡單黎曼解的概念提出了一種熵保正Godunov 型格式，這一格式對拉氏和歐拉MHD 系統都可以保接觸間斷。近些年來，有一些保正拉氏格式[4,9]被提出。這些格式可以很好的運作于歐拉方程并能得到高階精度。但是，所有這些格式都不能推廣到MHD 系統。

本文中，我們將關注的焦點放在針對于一維理想磁流體系統的保正拉氏算法設計上。基于文獻[10]中在拉氏框架下針對二維可壓縮理想MHD 方程組設計的RKDG 方法，我們推導出針對一維理想MHD 方程組的拉氏格式。之后，針對拉氏格式推廣了HLLD 近似黎曼解[7]，這一黎曼解可以保持密度和熱力學壓力的正性。這種拉氏HLLD 數值通量的表達式與其在歐拉框架下的表達式并不相同。運用這一特別的HLLD 數值通量，我們可以構造出一種保正拉氏格式。最后，我們將會給出幾個一維中具有挑戰性的數值算例來證明我們方法的有效性。

本文結構如下，在第1 節中，我們給出針對于一維理想MHD 方程組的拉氏格式。之后我們給出拉氏HLLD 數值通量的推導過程及其保正性質。最后，通過運用拉氏HLLD 數值通量，我們可以構造出求解一維理想MHD 方程組的保正拉氏格式。在第2 節中，通過給出數值算例可以證明我們方法的保正性質。最終，我們會在第3 節中給總結。

1 求解一維理想MHD 方程組的保正格式

1.1 一維理想MHD 方程組的拉氏格式

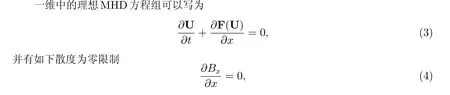
眾所周知，黎曼問題(8)真解的求解可能既困難又需要大量的計算，因此在構造Godunov 型數值格式時經常會使用近似黎曼解。基于HLLD 黎曼解[7]的良好性質，我們在針對一維MHD 系統的方法中使用此黎曼解。

1.2 拉氏HLLD 通量及其保正性質

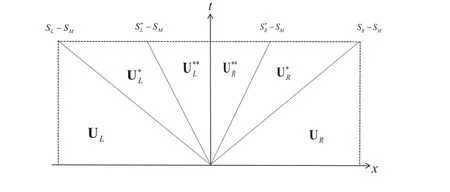
圖1 拉氏框架下HLLD 通量的黎曼扇

引理1 拉氏HLLD 求解器具有保正性質，如果SL和SR滿足

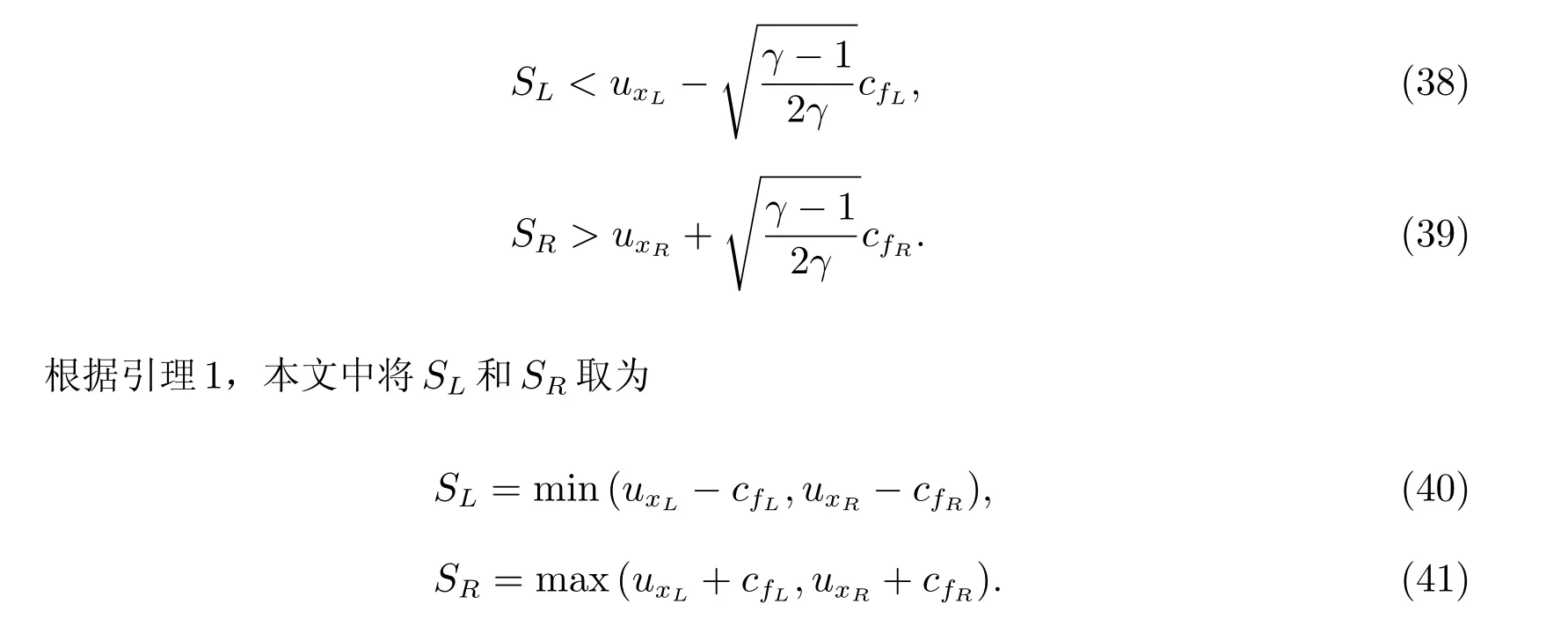
1.3 拉氏保正格式

我們將(7)中的Uh取為分片常數并運用向前歐拉時間離散，可以得到拉氏框架下積分弱形式(6)的離散格式

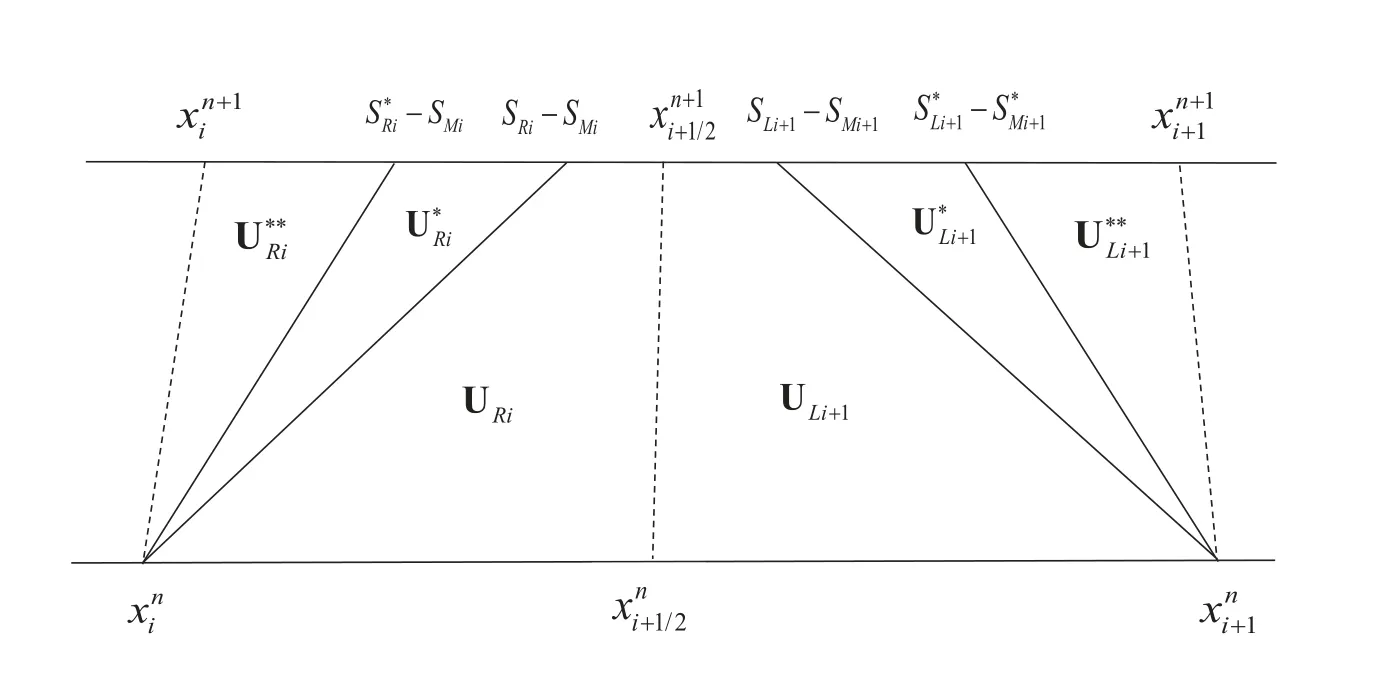
圖2 應用HLLD 求解器的拉氏格式在Ii×[tn,tn+1]中的波系演化

2 數值算例

在這一節中，我們給出幾個一維中具有挑戰性的數值算例來測試之前提出方法所具有的保正性質。若不使用保正方法，則所有這些算例在計算時都會產生負壓。

2.1 超快稀疏波問題

在這一小節中，考慮一個存在超快稀疏波的激波管問題。其初始條件如下

在圖3 中，我們分別給出u0= 3 和u0= 3.1 時在t= 0.05 時刻密度ρ，速度分量ux和總壓的圖像。如文獻[7]中所述，在對眾多近似黎曼解進行數值測試后可以發現，雖然在Mf= 3 時，所有測試過的近似黎曼解都不會產生負的密度和壓力，但是在Mf= 3.1 時有些卻無法計算下去。這是因為這些無法進行計算的近似黎曼解并不保正。在圖3 中可以看到我們的格式對于Mf=3 和Mf=3.1 都運算的很好，這一數值結果可以說明拉氏HLLD 黎曼解的保正性質。注意到，圖3 中的圖像與文獻[7]中所給出的圖像有所不同，這是因為本文中的結果是運用拉氏方法得到的，網格隨著流體移動到了計算區域兩端，在x=0 附近網格非常稀疏，x=0 附近密度趨于真空。

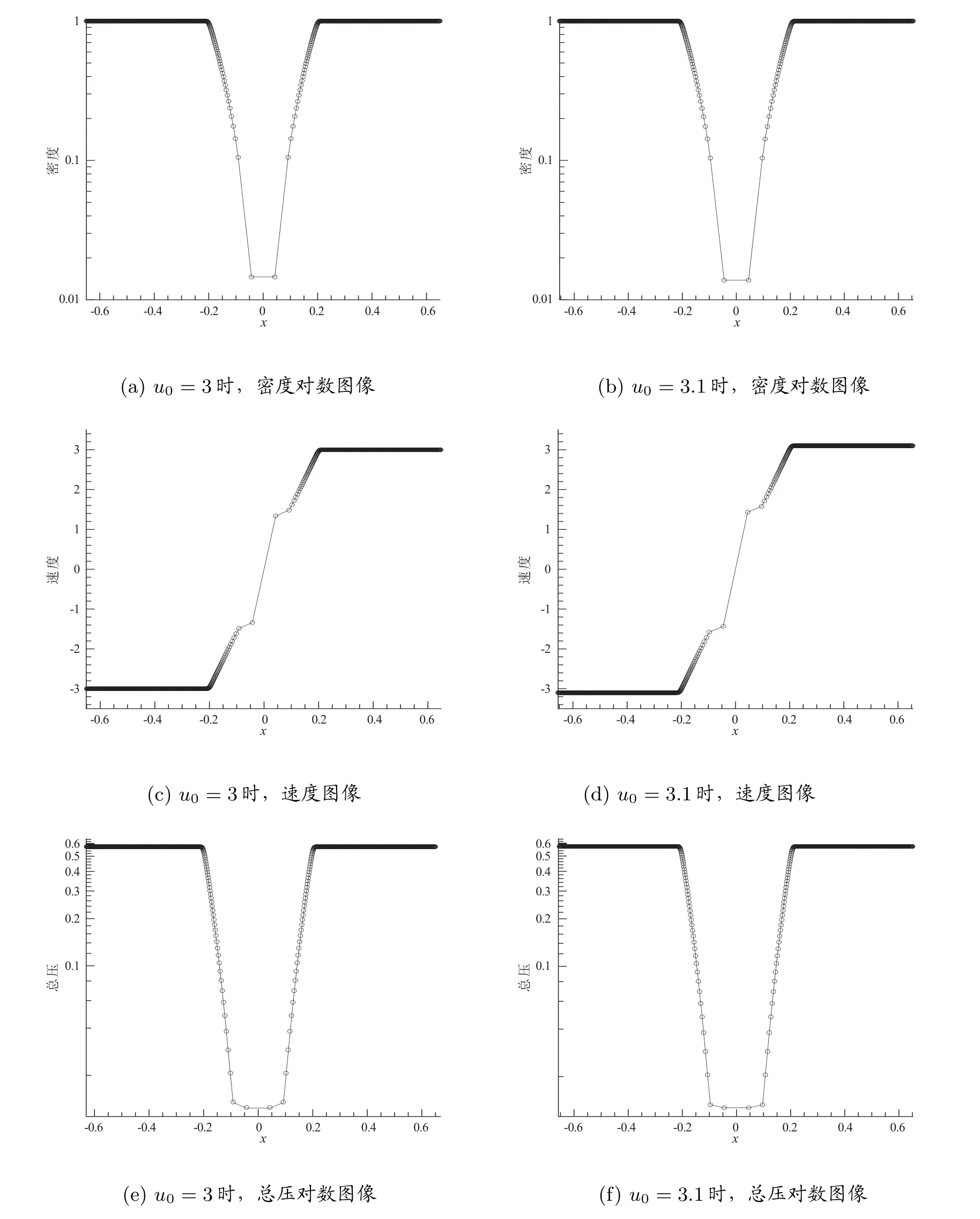
圖3 一維超快膨脹激波管問題的結果

2.2 一維真空激波管問題

在這一小節中，我們給出文獻[5]中提出的一維真空激波管問題的數值結果。問題的初始條件如下

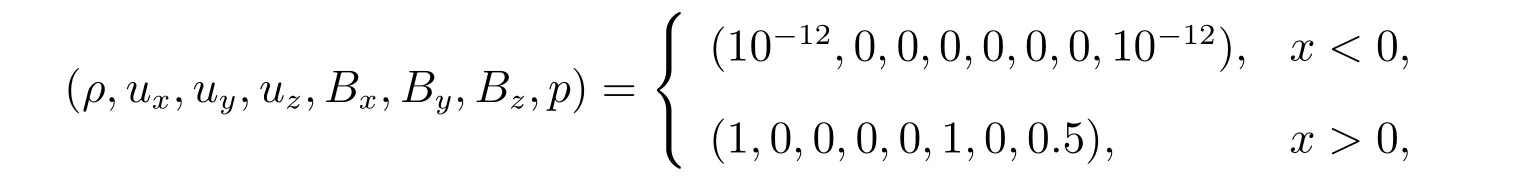
計算區域取為[?0.5,0.5]。γ= 5/3 并應用外流邊界條件。這一問題用來說明我們的拉氏保正格式可以處理擁有極低密度和壓力的問題。

在圖4 中，我們給出在t=0.1 時刻2 000 網格上計算得到的密度和壓力的數值結果。通過此圖可以觀察到，在x=?0.3 附近網格非常稀疏。與之前的數值算例類似，在拉氏方法中網格隨著流體移動，因此x=?0.3 附近趨于真空。通過和文獻[5]中的結果進行比較，我們可以確信無論是低密度還是低壓力都捕捉得很好。注意到，如果不運用保正方法來計算此問題，則計算程序將會因為非物理解的出現在幾個時間步內崩潰。

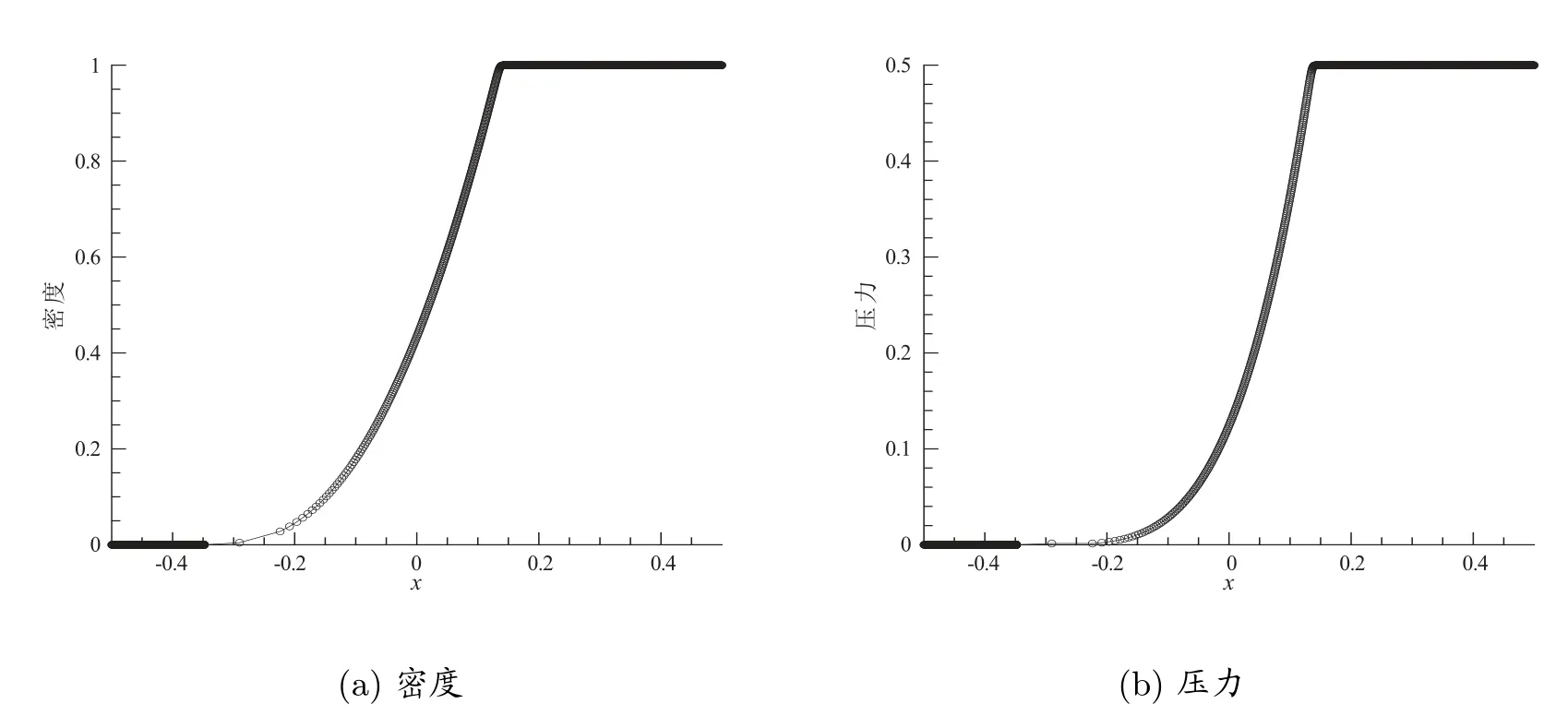
圖4 運用保正拉氏格式在2 000 網格上得到的一維真空激波管問題的密度和壓力

2.3 旋轉阿爾文波脈沖問題

本節，我們考慮文獻[1]中提出的旋轉阿爾文波脈沖問題。給出初始條件如下計算使用周期邊界條件，γ= 5/3。算例中，初始壓力比總能的萬分之一還要小。除此之外，該問題的解中還存在一個很強的阿爾文波間斷，大多數數值格式在計算此問題時都會產生負壓。

該問題的數值模擬采用了800 個計算網格。在圖5 中，我們給出拉氏保正格式在t=0.156 時刻得到的總能和壓力。注意到在解中存在兩個脈沖，因此成功的數值模擬應該能很好的保持這一特點。與前面的數值算例類似，如果不使用保正方法計算此問題，則計算程序會在幾個時間步內崩潰。

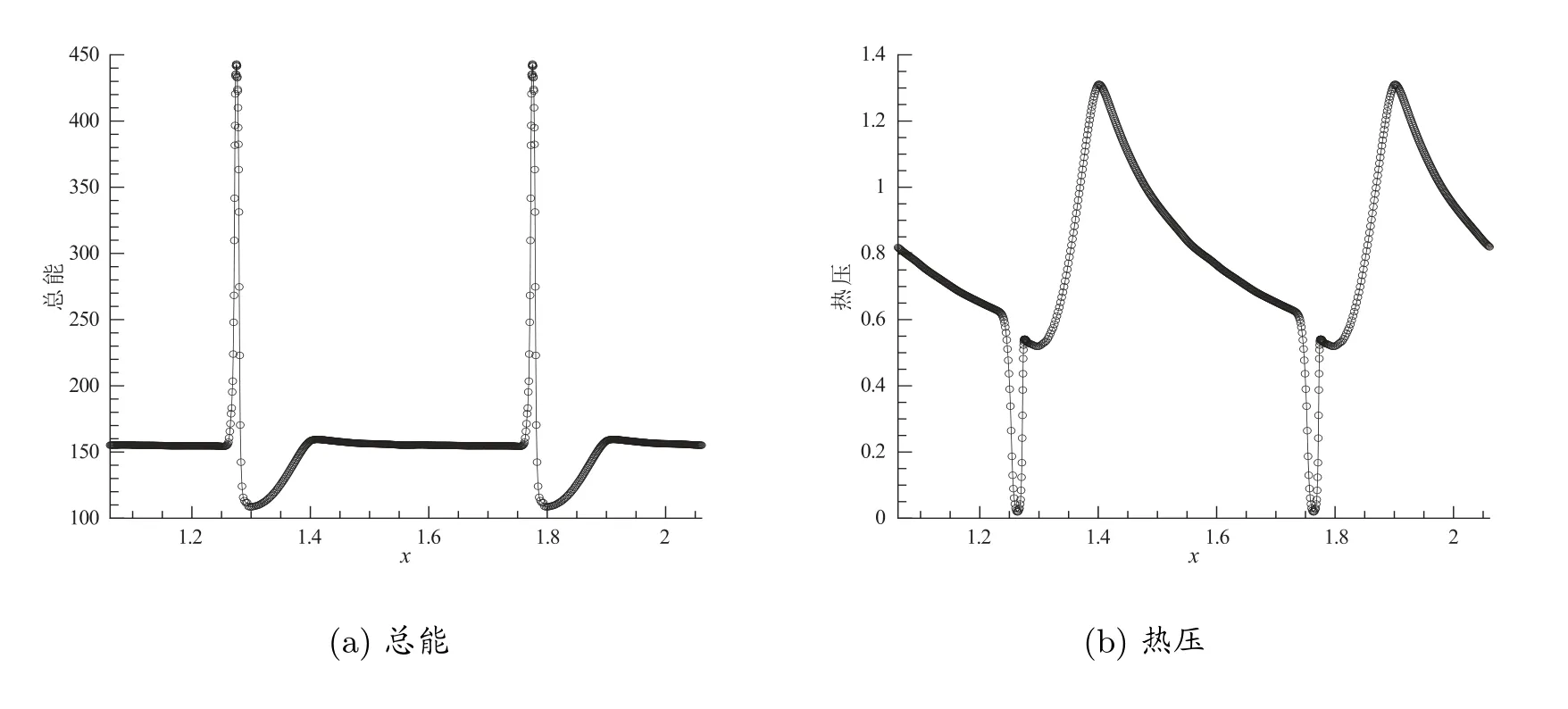
圖5 運用保正拉氏格式在800 網格上，t=0.156 時，計算得到的旋轉阿爾文波脈沖問題的總能和熱壓

3 總結

本文中，我們給出了一維理想MHD 系統的一種拉氏形式，并提出了一種在適當的信號速度下可以保持密度和熱力學壓力正性的拉氏HLLD 數值通量。運用這一HLLD 通量，我們構造出了一種針對一維理想MHD 系統的保正拉氏格式。最后，我們給出了幾個具有挑戰性的數值算例來證明本文提出的方法所具有的保正性質。

在將來的工作中，我們將會探索如何對于多維MHD 系統構造保正拉氏格式。在對拉氏MHD 系統特別是多維情形設計保證格式時存在數個困難。這些困難使得多維MHD 系統的保正拉氏格式構造變為了一個十分復雜的工作。因此，這一工作仍然需要繼續研究。