用數學之“鑰”，開生活之門

陳升見

時常聽到有些同學抱怨：學數學沒用，在生活中根本用不到。數學在生活中真的用不到嗎？我們來看幾個案例。

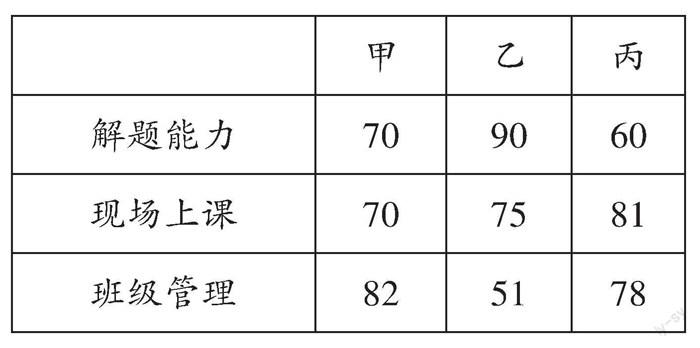
案例1：某校要招聘一名數學教師，對報名人員進行解題能力、現場上課、班級管理三個方面的考核，最優秀的三名應聘者成績如下：

學校應該聘用哪名應聘者呢？

【分析】三名應聘者各項成績的算術平均數依次是74、72、73，甲的分數高，那么學校一定選擇甲嗎？從各項成績看，甲比較均衡，但若學校特別需要講課好的教師，丙就比較合適，不過丙的解題能力測試成績很低，學校對其基本數學素養的水平有一定的擔心；又若學校需要解題能力很強的教師，顯然乙比較合適。在此情況下，學校可根據自己需要，對每個項目的重要程度賦予一定的“權”，例如，學校希望在衡量各項成績的基礎上，傾向于講課好一些的教師，因此將這三項成績按3∶5∶2的權重計算，三名應聘者的得分依次是72.4、74.7、74.1，則能選出需要的教師人選——乙。

【點評】本案例是學校經常面臨的問題，通過總分或算術平均數排名，有時并不能選出學校需要的人才。加權平均數是解決這類問題的重要工具，通過賦予每個項目不同的“權”，選出需要的人才。為保證公平，“權”數通常在成績出來以前確定。實際上，在真正評選時，學校一般先通過解題能力測試選出一批應聘者，再在面試環節通過賦予“現場上課”和“班級管理”不同“權”，選出需要的人才。生活中，學生的學期總評、單位招聘都會用到加權平均數，加權平均數是解決這類問題的一大利器。

案例2：某校要從兩名選手中選一名參加投籃比賽，故對兩人進行投籃能力測試，共比賽10場，每場投球20次，投中個數如下：

甲：12，13，11，15，10，16，13，14，15，11；

乙：11，16，6，14，13，19，17，8，10，16。

根據數據，選擇哪位選手參賽呢？

【分析】由計算可知[x]甲=[x]乙=13，s甲2=3.6，s乙2=15.8，兩名選手平均數一樣，但甲方差小，甲成績的波動性就小，發揮比較穩定，所以選擇甲參加比賽，成績會比較穩定；乙成績的波動性較大，但乙有三次成績不低于16次，甲只有1次，選乙參加比賽有取得高分的可能，但也有獲得低分的風險。

【點評】本案例是選拔運動員參加比賽時經常遇到的問題。對于射擊、舉重等項目，分析選手多次比賽數據，計算選手平時成績和比賽數據的平均數和方差，根據需要——穩定為主還是沖擊好成績為主選拔運動員。

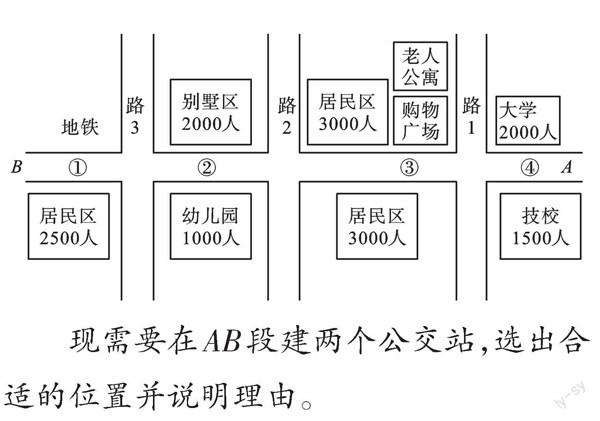
案例3：某地主干道AB兩旁的建筑用途及情況如圖：

現需要在AB段建兩個公交站，選出合適的位置并說明理由。

【分析】考慮實際情況：①處靠近地鐵，人流量大，路對面有居民需要乘坐公交車，要設公交站；②處幼兒園孩子離家較近、需要家長接送，而別墅區人員相對富裕，出門以私家車為主，對公交車需求較少，可不設公交站；③處人員密集且有購物廣場，人流量較大，要設公交站；④處人員以大學生為主，可步行至③，若條件允許，也可設公交站。

【點評】本案例是生活中常見的規劃問題，道路兩旁的具體情況需要我們用統計知識去收集數據、整理分析數據，最后做出判斷，從而增加設計的合理性。這類問題在生活中比比皆是，比如繁華路口紅綠燈時間的設計要以車流量為依據；公交車次的設計要根據不同時間段客流量的多少來安排，從而提高公共資源的利用率等。統計應用到生活，很多時候不需要精確的判斷，只需要粗略估計，做出合理的決策即可。

三個案例說明數學在生活中隨處可見，小到成績評估、選手的選拔，大到城市的規劃、防疫措施的制定等，都離不開數據的分析。因此，我們只有學好數學，才能讓數學更好地服務生活。

（作者單位：江蘇省南京市第五初級中學）