學習科學視角下的數學空間游戲設計與應用研究

尚俊杰 曾嘉靈 周均奕

[摘? ?要] 空間能力是信息時代下人才培養的關鍵之一，與數學學習聯系緊密，而立體圖形的折疊與展開是中國小學數學圖形與幾何教學的重難點。教育游戲環境能夠促進數學認知和空間能力發展。研究采用設計研究法，基于學習科學視角下教育學、心理學、認知神經科學在折疊與展開領域的相關研究成果，分析教育游戲相關理論構建認知、動機和調節的三維度游戲設計原則，設計開發了一款折疊與展開教育游戲《方塊消消樂》，并開展應用研究對游戲的實際效果進行了評估。研究分析了32名學生的成績數據發現，在每天40分鐘共三天的基于游戲教學干預后，學生的數學知識學習和心理折疊能力顯著提升，對于知識學習先驗能力低的學生提升效果尤為明顯。

[關鍵詞] 學習科學; 教育游戲; 游戲化學習; 數學認知; 圖形與幾何; 空間能力; 折疊與展開; 心理折疊

[中圖分類號] G434? ? ? ? ? ? [文獻標志碼] A

一、引? ?言

空間能力是人類的重要能力之一[1]，包含大量非語言認知能力，對于數學、工程、科學、技術能力等領域的成功至關重要[2-3]，尤其與數學能力聯系緊密[4-6]。認知神經科學研究發現，人們在加工空間任務和數學任務時會激活相似的神經通路[7-9]，表明空間能力和數學能力的緊密聯結可能基于更底層的共享過程。我國十分重視數學教育中空間與圖形知識的培養，在《義務教育數學課程標準（2011年版）》（新課標）中將“圖形與幾何”作為數學課程內容的四大領域之一，強調“幫助學生建立空間觀念”具有舉足輕重的地位。

然而，圖形與幾何部分也是小學數學教學中比較薄弱的環節，一方面小學生的抽象思維和空間思維能力尚未發展完全，空間想象能力較弱，對平面圖形和立體圖形的正確表征難以建立;另一方面教師在進行相關知識教學時也難以表述，使其成了教學難點之一。其中，立體圖形的折疊與展開更是難度排序第一的知識點[10]。研究發現，在折疊與展開的教學過程中，學生存在對于折疊與展開問題的想象困難;課堂教學中的動手操作只是流于形式;學生往往因課后練習出錯率高，逐漸失去對幾何的學習興趣等[11]。

近年來，游戲化學習備受關注，“寓教于樂”的教育游戲不僅可以激發學習動機，還能夠發展學生的認知能力[12]。此外，已有許多研究證實了游戲環境對空間能力的提升效果[12-15]。鑒于此，本研究以學習科學的多學科視角，基于教育學、心理學和認知科學領域的相關研究成果，對立體圖形折疊與展開的教學內容、認知機制進行分析，設計開發了一款適合小學五年級“立體圖形折疊與展開”內容學習的數學空間教育游戲《方塊消消樂》（曾用名：《方塊消消消》），并將該教育游戲應用于教育教學實踐，對其應用效果進行了評估。

二、理論基礎

（一）基于學習科學視角的折疊與展開學習

本研究從學習科學的跨學科視角出發，綜述了教育學、心理學和認知科學領域相關理論和研究成果，深入系統地分析了折疊與展開的學習過程，為折疊與展開教育游戲科學、有效的認知活動設計提供理論基礎。

1. 教育學視角

幾何學習和空間能力發展是小學數學課程的重要內容之一。對于立體圖形的折疊與展開這一學習內容，學習者需要掌握立體圖形（如長方體、正方體）的特征、認識立體圖形展開圖、在展開圖中找到各組相對的面等知識點[16]。在教學的過程中，教師需要重點關注學習者感受和想象將立體圖形表面展開的過程，幫助學生感受圖形在二維平面和三維立體之間展開和折疊的運動變化[17]。整個運動變化過程是學習的重點，同時引導學生深入了解立體圖形的特征，培養學生的空間能力。

為了達到以上的教學目標，研究者們設計了剪紙盒、磁力片等多種教學方式[18-21]。已有研究也探討了學生在學習折疊與展開內容時出現的問題及可能成因，如高曉旭認為，由于學生缺乏獨立自主的操作訓練、教師缺乏對學生想象過程的確切指導等原因，學生會出現難以想象立體圖形變化過程、難以理解展開圖與立體圖面關系、難以描述折疊與展開動態過程等問題[11]。

因此，了解學生空間想象的認知過程是促進有效的數學學習和空間訓練的關鍵步驟。學生對立體圖形進行折疊與展開的過程，實際上是在進行心理折疊的過程，與心理折疊能力息息相關。

2. 心理學視角

心理折疊（Mental Folding）是一種復雜的空間可視化能力，是將二維的空間圖形和對象通過心理操作，轉換成三維的空間圖形和對象的信息加工過程[22]。心理學相關研究從心理折疊能力的發展和認知層面分析了學生在心理折疊任務時的表現，關注學生對二維圖形和三維物體的表征過程和加工模式。

心理折疊能力作為一種復雜的空間能力，會隨著年齡的增大而逐漸提高，其中8至9歲是學生從二維圖形認知向三維物體認知發展的重要階段。有許多因素可能會影響學生的心理折疊表現，比如折疊與展開的方向。根據Tversky提出的功能空間模型[23]，物體附著在三個身體軸上，包括頭/腳（head/feet）、前/后（front/back）和左/右（left/right）[24]。與左/右軸相比，有關頭/腳軸或前/后軸上物體的信息可以更快地被檢索到[25-26]。因此，學生較好處理前/后軸上的折疊，也比較好處理頭/腳軸的折疊，較難處理左/右軸的折疊[27]。折疊過程中涉及的正方形數目也會對心理折疊任務難度產生影響，每次動作所涉及的正方形數目越大，其難度越大[28-29]。此外，立體圖形的不同類型也會影響心理折疊的難度，其中立方體難度較小[30]，是學生認識立體圖形展開圖較好的切入點。

研究表明，空間能力可以通過與環境的交互得到發展[31]，同樣心理折疊能力也可以通過訓練提升，桌面游戲和計算機環境均對心理折疊能力的發展有促進效果[32]，如Yun等[33]發現，與傳統教學方法相比，VGLS（虛擬幾何學習系統）在提升中學生心理折疊能力方面具有明顯優勢。此外，教育游戲也是提升學生心理折疊能力的有效途徑之一。從感知重組和學習的視角理解空間概念的發展[34]，技術可以通過約束、反饋和目標結構系統幫助學生從非正式的感知特征轉變為更具規范性的特征[35]。而教育游戲可以為學生提供基于感知的體驗，能夠促進學生與概念本身的交互，有助于發展心理折疊能力[36]。

3. 認知神經科學視角

教育學和心理學分別從行為層面和認知層面分析了折疊與展開學習的過程，認知神經科學研究則從生理層面探究了折疊與展開學習的神經學基礎。眾多研究者應用腦成像技術研究學習者的大腦活動，探索心理折疊任務的基礎神經結構。腦電研究證明，心理折疊與大腦的頂葉區域有著密切的關系[37-39]。此外，Dan和Reiner應用腦電圖測量了學生在觀看2D或3D折紙演示視頻時的認知負荷指數，結果表明3D的演示視頻能夠顯著降低學生的認知負荷指數[40]，同時提升心理折疊能力。據此，本研究在教育游戲中設計了3D腳手架以促進學生的認知，輔助學生想象二維圖形和三維物體運動變化的過程，并減輕學生的認知負荷。

（二）教育游戲支持的折疊與展開學習

本研究立足于建構主義學習視閾，對教育游戲設計開發理論研究進行梳理。從教育游戲中的學習者信息加工模式、有效教學情境創設、學習動機激發和教師的促進引導作用四個方面討論教育游戲設計原則，以認知、動機和調節三個維度建構教育游戲設計理論框架（見表1），為折疊與展開教育游戲的有效設計提供參考和支持。

1. 認知設計

多媒體學習認知理論（Cognitive Model of Multimedia Learning）總結了多媒體學習中的認知過程和心理表征，根據學習科學的三項基本原則，包括雙通道原則、有限容量原則和主動加工原則，描述了多媒體環境學習是如何發生的[41-42]。當人們玩教育游戲時，可以在三種認知加工中分配有限的加工能力，包括無關加工、必要加工和生成加工。教育游戲在促進生成加工過程時起著重要作用，但容易產生無關加工過程。因此，教育游戲設計的目標是最大程度地減少無關加工，引發必要加工并促進生成加工。

由于教育游戲具有豐富的三維空間，教學內容主要通過視覺信息呈現，往往占據著學習者的視覺通道，因此在學習者與教育游戲進行交互時，同時進行有意義的聽覺和視覺輸入可能對學習者的注意力造成破壞[43]。好的教育游戲會使用環境音樂來調節聽覺通道，但需要注意環境音樂和音效的有效設計，以減少無關加工。另外，由于學習者每次在一個通道內只能處理少量信息，應注意避免同時呈現過多的學習材料，增加學習者的認知負荷，以保證必要加工過程的順利進行。

本研究基于多媒體認知理論，分析學習者在教育游戲中的信息加工模式，提出了教育游戲設計開發的認知設計原則，見表1中1-1、1-2。

2. 動機設計

情境認知理論認為，將學習置于知識產生和運用的特定物理或社會情境中，才可能發生有意義的學習。受情境認知理論的影響，教育游戲的設計主張將知識與情境融合，模擬真實的應用情境，設計虛擬的仿真場景，使學習者在與學習情境的交互中進行有意義學習，實現知識與技能的有效遷移。在教育游戲的設計中，可以通過給予玩家身份（Identity）吸引其思維，使其相信自己在游戲情境中是一個獨特的個體[43]，促進學生在教育游戲中的投入。

心流理論（Flow Theory）指出，當人們在進行某些日常活動時會完全投入到情境當中，注意力高度集中，并且過濾掉所有與活動不相關的知覺，進入到一種心流狀態[44-45]。心流是學習的最佳狀態，可以通過內在滿足感使學習者在從事任務時不停探索，不斷達到新的目標，最大化提高學習效率和學習深度[46]。基于心流理論，在教育游戲的設計中應該遵循以下規律：（1）概念和內容的復雜性是逐漸增加的，隨著個人技能水平的提高，挑戰水平也隨之提高，從而在無聊和沮喪狀態之間產生動態的張力;（2）游戲的規則必須明確，使學習具有可復制性，幫助學生探索環境和物體;（3）向學生提供明確的目標;（4）向學生提供快速、清晰的反饋，使學生知道自身目前的進度，以及成功完成任務還需要做什么努力;（5）游戲界面設計（即用于操縱游戲的控件）盡可能清晰和用戶友好，以減少無關加工[47-48]。

本研究基于情境認知理論和心流理論，分析內在動機的激發方式，提出了教育游戲設計開發的動機設計原則，見表1中的2-1至2-6。

3. 調節設計

Kolb提出了體驗學習理論，用學習循環模型來表示體驗學習的過程，主要包含四個步驟：具體體驗、觀察反思、形成抽象概念和在新情境中檢驗[49]。其中，反思是體驗學習的核心，在教育游戲中鼓勵批判性思維會影響更多長期記憶通道。當學習者利用現有知識庫（模式）在教育游戲中學習時，將獲得新的體驗，并將其與他們先驗的知識和經驗聯系起來，進行有效組織，從而吸收游戲中嵌入的學習內容，這就是學習者在教育游戲中的自我調節學習過程。在基于教育游戲的學習中，教師扮演著指導者的角色，負責促進和引導學習[50]。根據對教育游戲自我調節學習過程的分析，教師在課堂上應負責：（1）根據學習者獨立完成任務的情況，創建知識腳手架;（2）設計小步子教學指導，為學習者提供表達和反思的機會;（3）在學習者完成所有任務前，提供學習支持，答疑引導。另外，為了及時給學習者提供學習支持與反饋、指導教學和評估學習，應根據教學需求，在教育游戲中設計恰當的數據收集點，以收集到需要的反饋、評價數據。

本研究基于體驗學習理論，分析教師的促進引導作用，提出了教育游戲設計開發的調節設計原則，見表1中的3-1至3-4。

三、教育游戲設計研究

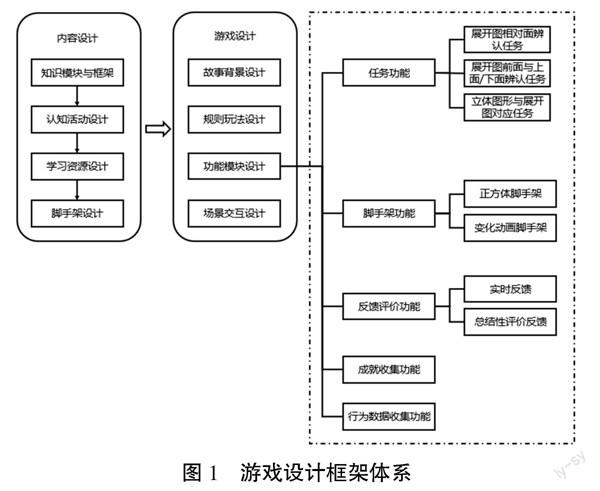
基于學習科學和教育游戲的理論基礎，本研究設計開發了這款促進小學五年級學生折疊與展開學習的教育游戲《方塊消消樂》。該游戲的設計圍繞內容設計和游戲設計兩個方面展開，其中內容設計是游戲整體設計的基礎。游戲的設計框架如圖1所示。

首先，在游戲的內容設計方面，本研究基于《義務教育數學課程標準（2011年版）》的學習內容標準和學段學習要求，開展了對人教版和北師大版教材的教學內容分析。經過整合分析結果，進一步總結與拓展，得到折疊與展開教育游戲的教學內容與組織順序，基于此構建知識模塊與框架，設計每個知識模塊的認知活動，開發認知活動相應的學習資源，并針對學生認知困難的點設計腳手架，以支持學習。

其次，圍繞著游戲的內容，貼合著目標概念學習，本研究開展了游戲總體元素的設計，包括故事背景的創設，搭建學習情境;設計游戲形式與規則玩法;體現游戲核心的功能模塊設計;具體化游戲設計表現的場景交互設計。功能模塊設計是教育游戲實現教育目標的重要部分，本游戲的功能包括任務功能、腳手架功能、反饋評價功能、成就收集功能和行為數據收集功能。游戲整體設計旨在使學習內容與游戲元素相互呼應，實現教育游戲內容概念與游戲的有效整合。相比于平衡游戲的教育性與游戲性，本研究旨在促進教育性與游戲性的融合發展。

（一）游戲內容設計

基于國家課程標準折疊與展開內容學習要求，本研究從目標定位、教學內容、教學序列和空間對象表征方面對兩版教科書進行對比分析，確定采用正方體作為空間概念的表征方式，及以逐層遞進、逐漸抽象的方式組織的三個教育游戲知識模塊：展開圖相對面的辨認、展開圖前面與上面/下面的辨認、立體圖形與展開圖的對應。通過不同類型的任務對同一空間概念進行表征，為學生提供豐富的認知機會，促進學生思維發展。

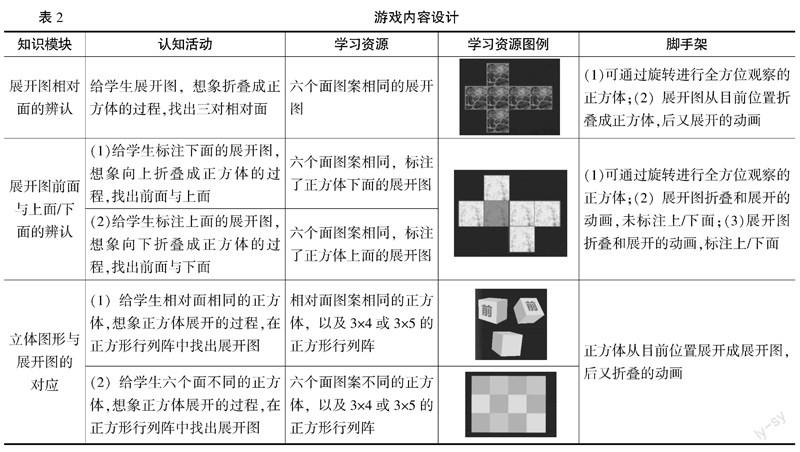
參考基于學習科學視角的折疊與展開學習研究，針對每個知識模塊開展認知活動設計。為了給予學生想象圖形運動變化過程的最大空間，所有學習活動均呈現靜態平面圖形與可觀察的立體圖形，將圖形動態變化過程保留給學生進行想象。在認知活動設計中，綜合考慮了學生的年齡特征與任務難度的影響因素。遵循學生的年齡發展規律，在學習過程中逐漸增加難度，實現學生思維從具體到抽象的過渡;考慮到折疊與展開方向和每次操作所涉及的正方形數目是影響任務難度的兩個因素，對任務難度進行排序，并根據難度排序進行關卡設計。具體的認知活動設計見表2。

學生在教育游戲環境中通過學習資源直接與學習內容進行交互，構建空間概念表征，因此游戲的學習資源設計在內容框架和認知活動的基礎上開展，主要為正方體平面展開圖、可旋轉觀察的正方體及正方形行列陣，見表2。

為了幫助學生解決認知困難、促進學生對二維圖形和三維物體運動變化過程的理解和表征，本研究設計了兩種認知腳手架，分別為可旋轉觀察的正方體和二維圖形與三維物體運動變化過程的演示動畫。例如，在展開圖相對面的辨認模塊中，游戲提供了可通過旋轉進行全方位觀察的正方體，幫助學生建立對平面圖形和立體圖形的表征，輔助進行二維圖形和三維物體表征的轉換;以及展開圖從目前位置折疊成正方體，后又展開的動畫，幫助學生進行平面圖形和立體圖形轉換的想象，突破認知困難。

（二）游戲整體設計

1. 故事背景創設

故事背景創設能夠為學生提供在教育游戲世界中獨特的個體身份，增強代入感，提升學習動機，是保證游戲其他設計效果的基礎。《方塊消消樂》將學生設定為勇闖混沌的庫布（Cube）世界的勇士，并提供八款游戲化身選擇，學生可以選擇其一開始游戲，與邪惡勢力斗爭，找尋被封印的12神獸，守護庫布世界。

2. 規則玩法設計

基于對學習者的分析，《方塊消消樂》目標對象為小學五年級學生，為了在游戲過程中，盡量減少學生在操作和規則理解上的困難，應設定清晰明確的游戲規則，保持學生的注意力和興趣，并將主要玩法設計得簡單且易于操作。因此，本游戲采用消除游戲的形式，學生在游戲中會遇到基于每一關卡圖形庫隨機生成的圖形，玩家需要在限定的步數內消除足夠多的正方形。根據每一個知識模塊的任務要求，學生需在圖形中找出、消除對應的面，如果選擇正確，相應的面被消除，玩家累積得分，步數減少，進行下一個任務或圖形挑戰;反之，玩家的機會步數減少，進行同一個任務挑戰。游戲結束，根據玩家得分進行總結性評價反饋，評判星級，并進行關卡物品獎勵。

3. 功能模塊設計

游戲的功能模塊設計是支持教育游戲有效運作、達到教學目標的關鍵，《方塊消消樂》游戲主要包括任務功能、腳手架功能、反饋評價功能、成就收集功能和學生行為數據收集功能。

其中，任務功能是教育游戲的核心功能，也是學生進行認知活動的功能。如前文所述，本游戲中包括三種任務：展開圖相對面辨認任務、展開圖前面與上面/下面辨認任務和立體圖形與展開圖對應任務，以闖關模式作為其具體表現形式，設計對應的三個地圖：火焰山、冰川島和水晶巖洞。

腳手架功能是支持學生進行折疊與展開學習，幫助突破認知困難的功能。如前所述，本游戲設計了兩種腳手架支持：可觀察的正方體和平面圖形與立體圖形變化過程動畫，旨在幫助學生建立對平面圖形和立體圖形的表征，建構表征相互轉換的過程。根據三種任務要求，設計漸進的腳手架，表現在游戲中為不同難易程度的提示，見表2。需要注意的是，當學生使用了正方體腳手架提示時，本次操作得分減半;當學生使用了折疊與展開動畫腳手架提示時，本次操作不得分。

反饋評價功能是學生獲得學習反饋以調整學習過程的功能，包括闖關過程中的實時反饋和闖關結束后的總結性評價反饋。闖關過程中的實時反饋表現在學生進行圖形選擇后，如果選擇正確則圖形消除、出現選擇正確游戲音效、得到積分獎勵，如圖2（a）所示;如果選擇錯誤則圖形不消除、出現選擇錯誤游戲音效、不積分，并顯示錯誤提示，以幫助學生發現認知錯誤，及時構建正確概念，如圖2（b）所示。總結性評價反饋發生在學生闖關結束后，對學生在這一關的學習表現進行評星打分，提供學習結果反饋。

成就收集功能是為學生設置的隨機通關獎勵，能夠有效激發學生的學習動機。每個關卡都設有通關物品獎勵，如地圖碎片、護身符、神獸等，學生可以在背包處查看已獲得的通關獎勵。學生行為數據收集功能則是教師獲得教學反饋、調整教學的重要參考，也是教育游戲評價的數據基礎之一，能夠提供客觀有效的學習行為數據。本游戲設計了學生行為數據采集點，一方面記錄關卡內學生的任務完成情況，包括學生每次操作的時間、圖形、正誤情況、選擇情況等;另一方面記錄學生關卡任務完成外的行為情況，包括提示、暫停、重新開始、背包等。

4. 場景交互設計

基于理論基礎中確定的教育游戲設計理論框架，開展場景交互設計。《方塊消消樂》共設計了9種場景界面，如游戲入口界面、關卡選擇界面、游戲主界面、游戲結果界面等，每一種界面都承載著游戲的不同功能，共同組成了完整的游戲架構。

四、教育游戲應用研究

為了檢驗《方塊消消樂》折疊與展開學習的效果，本研究將此游戲應用于小學五年級課堂教學，開展了實驗研究，以評估《方塊消消樂》對提升學生數學知識學習和心理折疊能力的效果。并嘗試探究《方塊消消樂》對具有不同先驗能力的學生，是否會產生不同的影響效果。根據研究目的，本研究采用前后測實驗設計，并提出兩個研究假設。假設一：學生的知識學習和心理折疊能力后測成績都顯著高于前測成績;假設二：對于先驗能力低的學生，其知識學習和心理折疊能力的提升效果都顯著高于先驗能力高的學生。

（一）研究設計

1. 研究對象

本研究在北京市一所公立小學的五年級開展，隨機選取了一個班級共37名學生參與實驗，其中女生20名，男生17名。由于整個實驗周期（包括前測、干預和后測）持續11天，存在一些學生無法完成整個實驗的情況，所收集到的數據反饋不完全，無法納入分析過程，作剔除處理。完整參與研究的總人數為32人，其中女生15名，男生17名。該所小學使用北京版教材，尚未完成“立體圖形的折疊與展開”內容的學習。

2. 研究工具

為測量學生的知識學習成績，研究參考小學五年級折疊與展開內容的習題和試題，在小學數學教育專家的指導下，開發了學習成效測試，共包含11道題目，分別為6道選擇題和5道填空題。每道題目計1分，測試總分為11分，學生的測試成績為正確回答題目的累計分數。針對前測和后測開發了兩版學習成效測試，保持試題數目、類型、測試內容和難度相同，題目中具體圖形和答案不同。

為評估學生的心理折疊能力，研究選取了應用最為廣泛的紙張折疊測試（Paper Folding Test）[51]作為測量工具，共包含20道題目。測試總分為20分，學生的測試成績為正確回答題目的累計數目減去錯誤回答數目的五分之一。測試題目被分為兩部分，每部分有10道題目，呈現在同一頁上，計時3分鐘完成。每道題目給出一張正方形紙的折疊和打孔方式，學生需要想象打孔后的紙張展開過程，并在五個答案中選擇展開后的正方形紙。

3. 研究過程

實驗前測在實驗干預的前一周進行，即第一天，學生進行了知識學習和心理折疊能力的前測，分別用時為14分鐘和6分鐘。在第八天至第十天，開展三天的實驗干預，學生每天進行1課時的基于《方塊消消樂》的學習，持續時間40分鐘。第八天為新授課，由教師開展基于《方塊消消樂》的折疊與展開內容教學;第九天和第十天為練習課，學生獨立進行基于《方塊消消樂》的學習，教師作為引導者的角色，為學生答疑解惑，提供學習支持。干預結束后，第十一天，學生進行知識學習和心理折疊能力的后測，用時與前測一致。

（二）研究結果

1. 教育游戲應用效果

本研究采用配對樣本t檢驗對學生前后測數據進行分析，以探究教育游戲的應用效果。結果見表3，學生知識學習的后測總分均值（M=9.63，SD=1.29）顯著高于前測（M=6.00，SD=2.78），t（31）=-8.618，p=0.000，d=1.524;心理折疊能力的后測總分均值（M=10.85，SD=4.23）顯著高于前測（M=8.38，SD=4.33），t（31）=-5.075，p=0.000，d=0.897。研究結果證明了研究假設一，學生的知識學習和心理折疊能力后測成績都顯著高于前測成績，說明教育游戲《方塊消消樂》的應用能夠提升學生的數學知識學習和心理折疊能力。

2. 不同能力學生對比

本研究采用獨立樣本t檢驗，對高先驗能力學生和低先驗能力學生的前后測分數差（后測—前測）進行分析，以探究教育游戲對具有不同先驗能力學生的影響效果。由于樣本量未達100人，本研究分別按照前測知識學習分數和心理折疊能力分數，以50%為界將學生分為高能力組（16名）和低能力組（16名）[52]。結果見表4，知識學習先驗能力低的學生分數提升均值（M=5.31，SD=1.92）顯著高于先驗能力高的學生（M=1.94，SD=1.39），t（30）=-5.69，p=0.000，d=2.01;心理折疊先驗能力低的學生分數提升均值（M=3.00，SD=2.84）與先驗能力高的學生（M=1.95，SD=2.66）無顯著差異，t（30）=-1.08，p=0.289。研究結果部分證明了研究假設二，對于知識學習先驗能力低的學生，《方塊消消樂》應用的提升效果顯著高于知識學習先驗能力高的學生;不過《方塊消消樂》的應用對于心理折疊先驗能力不同的學生，提升效果無顯著差異。

五、結論與討論

（一）研究總結

本研究基于學習科學視角設計開發了一款科學、有效、有趣的教育游戲《方塊消消樂》。在學習方式上，游戲結合了學習科學領域對折疊與展開學習過程的研究結果，以遵循學生認知發展規律的方式有效建構空間概念;在學習內容上，游戲基于我國設定的課程標準與權威教材進行了詳細的教學內容設計分析，以保證內容基礎的適切性;在游戲設計上，本研究分析提出了教育游戲設計開發的認知設計原則、動機設計原則和調節設計原則，以實現教育性與游戲性的融合。在此基礎上，本研究將游戲與課堂教學整合，開展了教育游戲的應用效果評價。結果顯示，《方塊消消樂》可以有效地提升學生的數學知識學習和心理折疊能力。在知識學習上，相比于先驗能力高的學生，《方塊消消樂》對先驗能力低的學生提升效果更佳，而對于心理折疊能力來說，《方塊消消樂》對于先驗能力不同的學生具有相同的提升效果。

學習科學作為一個研究教與學的跨學科研究領域，整合了教育學、心理學、認知科學、腦科學等眾多領域研究成果。如何將學習科學理論落實在具體的教育游戲設計中，以學習科學理論指導學生在教育游戲中學習，是每一個教育游戲實踐者都必須要思考的問題。在教育游戲的設計開發中，實踐者需要梳理學習內容，總結學生學習過程中遇到的問題與困境，然后以問題為錨點，分析學生認知規律與認知水平。以學習科學相關理論為基礎建構教育游戲的整體邏輯框架，從而搭建理論與實踐之間的橋梁。

（二）研究啟發

回顧本研究可以發現，教育游戲設計是從理論到實踐不斷落地的過程。從理論研究開始，結合需求分析，最終完成游戲的設計與開發，以實現科學、有效、有趣的教育游戲。據此，本研究得出以下教育游戲設計的啟發：

1. 理論研究是教育游戲設計開發基礎

教育游戲設計開發過程的理論基礎包括學習內容相關理論和教育游戲設計理論。學習內容相關理論能夠幫助研究者了解學生的學習過程和認知方式，從而設計科學的認知活動支持學生的概念建構，保證教育游戲的科學性。本研究中《方塊消消樂》的設計基于學習科學的跨學科研究成果，探究學生二維、三維圖形表征建構和心理折疊能力認知過程，以及折疊與展開教育教學問題及成因，總結出設計開發教育游戲認知活動的理論基礎。教育游戲設計理論是游戲總體設計的參考，為教育游戲的有趣性提供支持。本研究立足于建構主義學習視域，基于多媒體認知理論分析學習者在教育游戲中的信息加工模式，基于情境認知理論和心流理論分析內在動機的激發方式，基于體驗學習理論分析教師的促進引導作用，從認知設計、動機設計、調節設計三個方面提出教育游戲設計開發的原則，為營造科學有效的學習環境提供支持。

2. 需求分析是教育游戲有效應用的保障

在研究目標內容相關理論的同時，應開展對目標知識內容的教學和學習的需求分析。通過需求分析，建構教育游戲設計開發的內容基礎，貼合目標需求進行教育游戲的認知活動設計，從而保證教育游戲的有效性和實用性。本研究從中國數學課程標準出發，分析人教版和北師大版小學五年級數學教科書，梳理“立體圖形折疊與展開”相關部分的教學設計思路，明確教學目標、教學內容和學習深度范圍，為構建教育游戲的學習內容框架、設計符合學生認知發展的認知活動與相應的學習資源和腳手架提供參考。

3. 設計開發實現教育性和游戲性的融合

相比于將教育游戲的教育性和游戲性作為兩個排他的因素進行平衡，本研究旨在推動教育性和游戲性的融合，從而實現兩方面的交互發展。理論研究與需求分析為教育游戲設計開發提供了理論基礎和內容基礎，指導游戲的內容設計和總體設計。教育游戲的設計開發應以目標知識的內容設計為基礎，貼合教學內容設計開展游戲總體設計，促進學習者發現知識本身的樂趣，從而激發內部動機。本研究立足于游戲的內容設計，開展貼合學習內容的游戲總體設計，融合發展教育性與游戲性。

（三）研究不足與反思

由于時間限制，本研究設計的游戲并沒有得到大范圍的測試，尚未開展后續教學工作;另外，游戲內容和規則還需要結合學生學習情況進行適應性的修改。因此，本研究設計的折疊與展開游戲還需要進一步的迭代優化和改進，如在游戲設計上，可以豐富游戲規則，探索漸進性玩法，以增強游戲趣味性;在內容設計上，可以利用游戲后臺數據對學習內容的理論分析進行補充和完善，提升內容設計的科學性和有效性。在未來研究中，研究者可以通過迭代的優化以實現螺旋上升的游戲設計，最終落實到一線教育教學實踐，進一步助力學生數學學習和空間能力的培養。

致謝：在研究過程中，感謝北京市順義區西辛小學朱秋庭校長、劉學紅校長、李云龍主任、付秀芳老師、張麗麗老師、趙海平老師、趙麗老師提供的指導、支持和幫助;感謝北京市順義教育研究考試中心教研員周愛東老師、深圳市福田區教育科學研究院小學數學教研員姚鐵龍老師提供的建議和指導;此外，還要感謝胡若楠、夏琪、石長征、張媛媛等北京大學學習科學實驗室的老師、同學們給予的支持和幫助！

[參考文獻]

[1] 傅孟霞.培養兒童空間認知能力的數字化游戲設計[D].濟南：山東師范大學，2013.

[2] WAI J， LUBINSKI D， BENBOW C P. Spatial ability for STEM domains： aligning over 50 years of cumulative psychological knowledge solidifies its importance[J]. Journal of educational psychology， 2009， 101（4）：817-835.

[3] TOSTO M G， HANSCOMBE K B， HAWORTH C M A， DAVIS O S P， PETRILL S A， DALE P S， MALYKH S， PLOMIN R， KOVAS Y. Why do spatial abilities predict mathematical performance？[J]. Developmental science， 2014， 17（3）： 462-470.

[4] TURGUT M. Development of the spatial ability self-report scale（SASRS）： reliability and validity studies[J]. Quality & quantity， 2015， 49（5）：1997-2014.

[5] GUNDERSON E A， RAMIREZ G， BEILOCK S L， LEVINE S C. The relation between spatial skill and early number knowledge： the role of the linear number line[J]. Developmental psychology， 2011， 48（5）：1229-1241.

[6] MIX K S， CHENG Y L. The relation between space and math： developmental and educational implications[J]. Advances in child development and behavior， 2012， 42：197-243.

[7] HUBBARD E M， PIAZZA M， PINEL P ， DEHAENE S. Interactions between number and space in parietal cortex[J]. Nature reviews neuroscience， 2005， 6（6）：435-448.

[8] BUETI D， WALSH V. The parietal cortex and the representation of time， space， number and other magnitudes[J]. Philosophical transactions of the royal society b-biological sciences， 2009， 364（1525）： 1831-1840.

[9] UTTAL D H， MEADOW N G， TIPTON E， HAND LL， ALDEN AR， WARREN C， NEWCOMBE NS. The malleability of spatial skills： a meta-analysis of training studies[J]. Psychological bulletin， 2013， 139（2）：352-402.

[10] 曾嘉靈. 基于學習科學視角的數學空間能力教育游戲設計與應用研究——以小學五年級“立體圖形的折疊與展開”為例[D].北京：北京大學，2020.

[11] 高曉旭.小學生幾何圖形折疊與展開困難的原因分析與對策研究[D].濟南：山東師范大學，2018.

[12] 尚俊杰，張露.基于認知神經科學的游戲化學習研究綜述[J].電化教育研究，2017，38（2）：104-111.

[13] GAGNON D. Videogames and spatial skills： an exploratory study[J]. Educational communication and technology journal， 1985， 33（4）： 263-275.

[14] FENG J， SPENCE L， PRATT J. Playing an action video game reduces gender differences in spatial cognition[J]. Psychological science， 2010， 18（10）：850-855.

[15] BOOT W R， KRAMER A F， SIMONS D J， FABIANI M， GRATTON G. The effects of video game playing on attention， memory， and executive control[J]. Acta psychologica， 2008， 129（3）：387-398.

[16] 田志明，朱小平.我們該教給學生什么？——對正方體展開圖的深入研討[J].小學教學參考：數學版，2010（3）：13-14.

[17] 錢建兵.有感于正方體展開圖的“另類”教學[J].小學數學教育， 2016（20）：48.

[18] 何忠云.關注"三量"，提質增效——小學高年級數學課堂教學有效性策略探究[J]. 內蒙古教育，2015（8）：70.

[19] 張少剛.合理操作 發展想象——“長方體和正方體的展開圖”教學片斷與思考[J].小學數學教育，2017（20）：59-60.

[20] 袁紅健.三問，在實踐中發展空間觀念——以“長方體和正方體表面的展開圖”兩次教學為例談對比思考[J].數學教學通訊，2017（31）：31-33.

[21] 丁偉， 李一鳴.“展開與折疊”教學實錄與評析[J].小學數學教育， 2018（Z1）：50-53.

[22] VOYER D， VOYER S， BRYDEN M P. Magnitude of sex differences in spatial abilities： a meta-analysis and consideration of critical variables[J]. Psychological bulletin， 1995， 117（2）：250-270.

[23] TVERSKY B. Structures of mental spaces —how people think about space[J]. Environment and behavior， 2003， 35（1）：66-80.

[24] FRANKLIN N， TVERSKY B. Searching imagined environments[J]. Journal of experimental psychology- general， 1990， 119（1）： 63.

[25] BRYANT D J， TVERSKY B， FRANKLIN N. Internal and external spatial frameworks for representing described scenes[J]. Journal of memory and language， 1992， 31（1）：74-98.

[26] NEWCOMBE N， HUTTENLOCHER J. Children's early ability to solve perspective-taking problems[J]. Developmental psychology， 1992， 28（4）：635-643.

[27] MA'RIFATIN S， AMIN S M， SISWONO T Y E. Students' mathematical ability and spatial reasoning in solving geometric problem[J]. Journal of physics conference series， 2019， 1157（4）：042062.

[28] SHEPARD R N， FENG C. A chronometric study of mental paper folding[J]. Cognitive psychology， 1972， 3（2）：228-243.

[29] ROBERTS J E， BELL M A. Two- and three-dimensional mental rotation tasks lead to different parietal laterality for men and women[J]. International journal of psychophysiology， 2003， 50（3）：235-246.

[30] FAW P J. A study of the development of the ability of selected students to visualize the rotation and development of surfaces[J]. Quality of life research， 1977， 6（6）：531-554.

[31] LIU A S， SCHUNN C D. The central questions of spatial cognition[J]. The oxford handbook of cognitive science， 2017，169：190.

[32] ARICI S， ASLAN-TUTAK F. The effect of origami-based instruction on spatial visualization， geometry achievement， and geometric reasoning[J]. International journal of science and mathematics education， 2015， 13（1）：179-200.

[33] YUN R， XI H， LI Y. The experiment of improving students' spatial ability by using VGLS[J].Advances in artificial reality and tele-existence， 2006，467-473.

[34] GOLDSTONE R L， LANDY D H， JI Y S. The education of perception[J]. Topics in cognitive science， 2010， 2（2）：265-284.

[35] VITALE J， BLACK J， SWART M. Promoting development of geometry concepts： interfacing multiple embodied representations with a computer game[J]. In Proceedings of the Annual Meeting of the Cognitive Science Society， 2011（33）： 33.

[36] BLACK J B， KHAN S A， HUANG S C D. Video and computer games as grounding experiences for learning[J]. Learning by playing： video gaming in education， 2014， 290-301.

[37] MILIVOJEVIC B，JOHNSON B W，HAMM J P，CORBALLIS M C. Non-identical neural mechanisms for two types of mental transformation： event-related potentials during mental rotation and mental paper folding[J]. Neuropsychologia，2003，41（10）：1345-1356.

[38] JAU？譒OVEC N， JAU？譒OVEC K. Sex differences in mental rotation and cortical activation patterns： can training change them？[J] Intelligence， 2012， 40（2）： 151-162.

[39] GLASS L， KRUEGER F， SOLOMON J， RAYMONT V， GRAFMAN J. Mental paper folding performance following penetrating traumatic brain injury in combat veterans： a lesion mapping study[J]. Cerebral cortex， 2012， 23（7）：1663-1672.

[40] DAN A， REINER M. Reduced mental load in learning a motor visual task with virtual 3D method[J]. Journal of computer assisted learning， 2017， 34（1）：84-93.

[41] MAYER R E. Applying the science of learning to multimedia instruction[J]. Psychology of learning and motivation： cognition in education， 2011， 55：77-108.

[42] MAYER R E. Computer games for learning： an evidence-based approach[M]. Cambridge： MIT Press， 2014.

[43] ANNETTA L A. The "I's" have it： a framework for serious educational game design[J]. Review of general psychology， 2010， 14（2）：105-112.

[44] CSIKSZENTMIHALYI M. Beyond boredom and anxiety. The experience of play in work and games[J]. Journal of individual psychology， 1977， 33（2）：267-268.

[45] ANNETTA L， MANGRUM J， HOLMES S，COLLAZO K， CHENG M T. Bridging realty to virtual reality： investigating gender effect and student engagement on learning through video game play in an elementary school classroom[J]. International journal of science education， 2009， 31（8）：1091-1113.

[46] FINNERAN C M. Flow in computer-mediated environments： promises and challenges[J]. Social science electronic publishing， 2013， 15（1）：82-101.

[47] PILKE E M. Flow experiences in information technology use[J]. International journal of human-computer studies，2004，61（3）：347-357.

[48] 馬穎峰，隋志華.基于Flow理論的教育游戲沉浸性設計策略研究——教育游戲活動難度動態調控研究[J].電化教育研究，2010，（3）：54-57，62.

[49] KOLB D A. Experiential learning： experience as the source of learning and development（Second Edition）[M]. NJ：Pearson FT Press， 2014.

[50] 張露，尚俊杰.基于學習體驗視角的游戲化學習理論研究[J].電化教育研究，2018，39（6）：11-20，26.

[51] EKSTROM R B， FRENCH J W， HARMAN H H. Manual for kit of factor-referenced cognitive tests[M]. Princeton， NJ： Educational Testing Services，1976.

[52] 吳明隆，涂金堂. SPSS與統計應用分析[M].大連：東北財經大學出版社，2012.

Research on Design and Application of Mathematical Spatial Games from Learning Sciences Perspective

SHANG Junjie，? ZENG Jialing，? ZHOU Junyi

（Lab of Learning Sciences， Graduate School of Education， Peking University， Beijing 100871）

[Abstract] Spatial ability is one of the keys to talent training in the information age and is closely linked to mathematics learning. However， it is found that folding and unfolding of three-dimensional figures is an important and difficult point in the teaching of graphics and geometry in Chinese elementary school. Educational game environments can promote the development of mathematical cognition and spatial ability. As a result， this study adopts the design-based research method， based on the relevant research results of pedagogy， psychology， and cognitive neuroscience research on folding and unfolding from the perspective of learning sciences， analyzes the theories related to educational games to construct the three-dimensional game design principles of cognition， motivation and regulation， and designs and develops a folding and unfolding educational game "Cube Elimination". An applied study is also conducted to evaluate the actual effect of the game. The study analyzes the performance data of 32 students and finds that the students' mathematical knowledge learning and mental folding abilities have been improved significantly after a 40-minute daily game-based instructional intervention for a total of three days， especially for students with lower initial knowledge proficiency.

[Keywords] Learning Sciences; Educational Games; Gamified Learning; Mathematical Cognition; Graphics and Geometry; Spatial Ability; Folding and Unfolding; Mental Folding

[作者簡介] 尚俊杰（1972—），男，河南林州人。研究員，主要從事學習科學與技術設計、游戲化學習、教育技術領導政策等研究。E-mail：jjshang@pku.edu.cn。

基金項目：北京市教育科學“十四五”規劃2021年度延續課題“基于學習科學和游戲化學習的學習能力培養研究"（課題編號： CEFA21067）