讓旋轉變換解決問題變得“有章可循”

郭紫嬌

摘? ?要：利用旋轉的方法解題是初中幾何變換問題中的一類典型問題，對綜合運用幾何知識進行分析的幾何直觀與空間想象力要求較高. 旋轉變換改變了圖形的位置，但是不改變圖形的形狀和大小，問題解決中常利用 “分散與集中”的化歸思想，通過旋轉變換將一些元素分散或集中，化解難以解決的幾何問題.

關鍵詞：旋轉變換;模型;思路;方法

1? 理解旋轉變換中的基本圖形

一個平面圖形F繞平面內一點O按一定方向（順時針或逆時針）旋轉一定角度得到圖形的變換稱為旋轉變換.由于旋轉變換中，對應點到旋轉中心的距離相等，則會存在一類常見的基本圖形——等腰三角形.

1.1? 旋轉變換的基本圖形1——等腰三角形

旋轉變換必存在以旋轉中心為頂角、對應點與旋轉中心連線為腰的等腰三角形.

如圖1，ΔABD繞著點B，按逆時針方向旋轉一定角度得到ΔCBE.

則 BD=BE，AB=CB，連接AC、DE后，ΔABC，ΔDBE是等腰三形.

解題中，可充分利用等腰三角形的性質思考問題.

1.2? 旋轉變換的基本圖形2——特殊的等腰三角形

如圖2，圖3，ΔABC繞著點A，按逆時針方向旋轉一定角度得到ΔA BC，由于旋轉前后對應點與旋轉中心連線所夾的角等于旋轉角，則∠BA B，∠CAC都是旋轉角.

①如圖2，當旋轉角為60°時，隱含兩個等邊三角形：ΔAB B，ΔAC C，從而可以得到等邊三角形的特有性質：三邊相等、三個角都是60°;

②如圖3，當旋轉角為90°時，隱含兩個等腰直角三角形：ΔAB B，ΔAC C，從而可以得到等腰直角三角形的特有性質：三邊的比例關系、兩個銳角都是45°.

2? 熟悉旋轉變換的常見模型.

2.1? 模型一：由等邊三角形旋轉60°，構造新等邊三角形

如圖4，已知ΔABC是等邊三角形，若要將ΔABC內部的ΔABD旋轉到外部，抓住目標圖形中的AB=AC，AB=BC兩個等量關系，有兩種方式：

（1）由AB=AC，公共頂點是點A，方向是從AB到AC，可以將ΔABD繞點 A逆時針方向旋轉60°得ΔACF，進而可得等邊ΔADF;

（2）由AB=BC，公共頂點是點B，方向是從AB到BC，可以將ΔABD繞點B順時針方向旋轉60°得ΔBCE ，進而可得等邊ΔDBE.

反之，對于外部圖形ΔACF，ΔBCE 同樣道理按反方向也可以旋轉到ΔABD.

2.2? 模型二：由等腰直角三角形旋轉90°，構造新等腰直角三角形.

如圖5，已知ΔABC是等腰直角三角形，∠BAC=90°.

（1）若要旋轉ΔABC內部的ΔACE，由AB=AC，公共頂點是點A，方向是從AC到AB，可以將ΔACE 繞點A順時針方向旋轉90°得ΔABD，進而可得等腰直角ΔADE;

（2）反之，若要旋轉ΔABC外部的ΔABD，由AB=AC，公共頂點是點A，方向是從AB到AC，可以將ΔABD繞點A逆時針方向旋轉90°得ΔACE.

2.3? 模型三：由正方形旋轉90°，構造等腰直角三角形

如圖6，圖7，已知四邊形ABCD是正方形.

（1）如圖6，若要旋轉正方形ABCD內部的ΔABP，有兩種方式：

①由AB=AD，公共頂點是點A，方向是從AB到AD，可以將ΔABP 繞點A逆時針方向旋轉90°得ΔADE;進而可得等腰直角ΔPAE;

②由AB=BC，公共頂點是點B，方向是從AB到BC，可以將ΔABP 繞點B順時針方向旋轉90°得ΔCBF;進而可得等腰直角ΔPBF.

反之，對于外部圖形ΔBCF，ΔADE同樣道理按反方向也可以旋轉到ΔABP .

（2）如圖7，若要旋轉正方形ABCD外部的ΔDCE，有兩種方式：

①由CD=AD，公共頂點是點D，方向是從DC到AD，可以將ΔDCE 繞點D順時針方向旋轉90°得ΔADF;進而可得等腰直角ΔFDE;

②由CD=BC，公共頂點是點C，方向是從DC到BC，可以將ΔDCE 繞點C逆時針方向旋轉90°得ΔCBG;進而可得等腰直角ΔGCE.

反之，對于外部圖形ΔBCG，ΔADF同樣道理按反方向也可以旋轉到ΔABP.

2.4? 模型四：以圓形的某邊中點旋轉180°，構造中心對稱圖形

如圖8，已知ΔABC中，點D是BC邊上的中點DC=DB，以D為旋轉中心可以將ΔACD旋轉180°得ΔADB.

3? 旋轉變換的應用

例1? 如圖9-1，點O是等邊ΔABC內一點，OA=3，OB=4，OC=5，證明：∠AOB=150°.

①分析條件：已知條件知道三邊長度，與結論要求角度似乎相差甚遠，且條件分散不好用，但三個數據使我們想到勾股數，若能將此三條線段集中到一個三角形就好了，由此聯系利用旋轉變換;

②觀察圖形：AB=AC=BC，等邊ΔABC三邊“等長共點”，具備多種旋轉方式，由于∠AOB為所求證，故OA，OB不動，遷移的目標圖形為OC，結合等邊ΔABC三邊“等長共點”，可以旋轉ΔBOC或ΔAOC;

③如何旋轉：如圖9-2，若旋轉ΔBOC，由AB=BC，公共頂點是點B，方向是從CB到AB，可以將ΔBOC繞點B逆時針旋轉60°得ΔBDA，進而可得等邊ΔDBO，OD=OB=4，AD=OC=5，易得ΔADO為直角三角形，問題解決.

方法借鑒：有等邊三角形則有相等的線段，為旋轉后能重合的線段提供了條件，再加上等邊三角形60°的角，為旋轉后再次出現等邊三角形提供了等量代換的條件，使得題目所有條件迅速貫通，問題輕松解決.如圖9-3，本題還可將ΔAOC旋轉，進一步體驗利用相等線段可以重合來構造旋轉解決問題.

變式1：如圖10-1，已知在ΔABC中，BC=a，AC=b，以AB為邊作等邊三角形ABD，且點D與點C位于直線AB的兩側，當∠ACB變化，求 CD的最大值及相應的∠ACB的度數.

①分析條件：已知條件知道兩邊長度，與結論要求角度似乎相差甚遠，且條件分散不好用，若能將BC=a，AC=b，以及要求的DC三條線段集中到一個三角形，進而利用三角形三邊的大小關系確定范圍，由此聯系利用旋轉變換;

②觀察圖形：等邊ΔABD三邊“等長共點”，具備多種旋轉方式，遷移的目標圖形為CD，結合等邊ΔABC三邊“等長共點”，可以旋轉ΔBCD或ΔACD;

③如何旋轉：如圖10-2，若旋轉ΔBCD，由AD=BD，公共頂點是點D，方向是從DB到AD，可以將ΔBCD繞點D逆時針旋轉60°得ΔEDA，進而可得等邊ΔECD，遷移CD=EC，從而建立已知與未知的三邊關系.

思路分析：考慮到等邊三角形的條件，有相等的線段，可考慮旋轉的方法，將ΔBCD繞點D逆時針旋轉60°，則點B與點A重合，得ΔBEA，則易得ΔECD為等邊三角形，CE=CD.

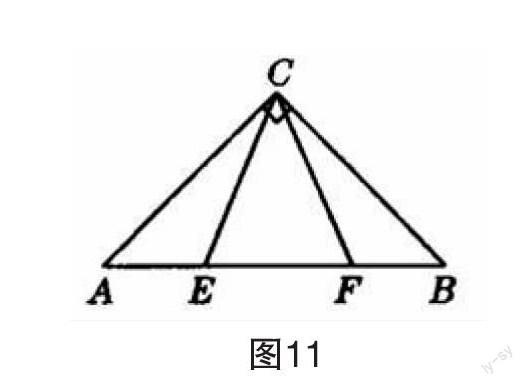
①當點E，A，C不在一條直線上時，有CD=CE

②如圖10-3，當點E，A，C在一條直線上時， CD有最大值，CD=CE=a+b.

此時∠CED=∠BCD=∠ECD=60°，∠ACB=120°.

因此當∠ACB=120°時，CD有最大值是a+b.

例2? 如圖11，ΔABC是等腰直角三角形，C為直角頂點.點E，F是線段AB上兩個動點（不與端點重合），且∠ECF=45°，點E，F的位置發生變化時，探究AE，EF，FB三者的數量關系.

思路分析：

①分析條件：從結論猜想可以將這三條線段集中到一個三角形中，證明其是直角三角形則問題得解;

②觀察圖形：等腰直角三角形中AC=BC，∠ACB=90°，具備了旋轉的條件;

③ 如何旋轉：如圖12，可將△CBF繞點C順時針旋轉90°得ΔCAM，再連ME，三條線段全部集中到了ΔMAE中，證出∠MAE=90°即可.

方法借鑒：等腰直角三角形中有相等的線段，也是利用旋轉來解題的常見背景，本題利用相等線段所在的三角形旋轉變換將分散的線段、角集中到了一個三角形中，再運用勾股定理證明. 本題還體現了動態幾何問題的一個共同特征：運動的圖形與靜止的圖形的相對位置雖然發生了變化，但有些結論仍然保持不變，且證明方法也是一樣的.這也正是動態幾何問題的魅力所在.

例3.如圖13所示，正方形ABCD的邊長為1，點F在線段CD上運動，AE平分∠BAF交BC于點E.

（1）求證：AF=DF+BE;

（2）設DF=x（0≤x≤1），ΔADF與ΔABE的面積和S是否存在最大值？若存在，求出此時的值及S的最大值;若不存在，請說明理由.

思路分析：

（1）①分析條件：求證AF=DF+BE，要證明兩條線段的和等于第三條線段，可以考慮截長補短的方法，使得DF，BE在同一直線;②觀察圖形：圖中正方形有相等的線段，具備旋轉條件;③如何旋轉：如圖14，將目標圖形ΔADF繞點A順時針旋轉90°得ΔABF'，再證明AF'= EF'即可（注意要證明E，B，F'三點共線）。（2）求S的最大值即求ΔAEF'面積的最大值，結合幾何圖形，高AB為定值，實際上就是要求EF'即A F'，也就是AF的最大值，顯然，當AF為對角線時取得最大值.由此可見，恰當的數形結合，能簡潔明了地解決問題.

方法借鑒：正方形各邊都相等，也是利用旋轉解題的常見情形，通常在正方形中存在共頂角圖形（或等腰三角形存在共頂點圖形）時，抓住正方形中相等的邊，把分散的線段所在的三角形進行旋轉從而將它們集中到一起，再運用全等三角形、勾股定理等知識解決問題.

例4：如圖15，在等腰ΔABC中，AB=AC，∠ACB=a，在四邊形中，DB=DE，∠BDE=2a，M為CE的中點，連接AM，DM.

（1）求證：AM⊥DM;

（2） 當a=_________時，AM=DM.

分析：⑴ M為CE的中點，可以旋轉180°，如圖16所示，在圖中畫出ΔDEM關于點M成中心對稱的圖形;

連接AD，AF，由中心對稱可知，ΔDEM≌ΔFCM，

DE=FC=BD，DM=FM，ΔDEM=FCM，

∵ ∠ABD=∠ABC+∠CBD

=a+360°-∠BDE-∠DEM-∠BCE

=360°-a-∠DEM-∠BCE，

∠ACF=360°-∠ACE-∠FCM=360°-a-∠BCE-∠FCM，

∴∠ABD=∠ACF，

∴ΔABD≌ΔACF，∴AD=AF，

∵DM=FM，∴AM⊥DM.

（2） 要使AM=DM，需有∠ADF=∠DAM=∠AFD=45°，∠BDE=2a=90°，a==45°.

方法借鑒：遇線段中點，具備等長共點特征，也是利用旋轉解題的常見情形，通過繞中點旋轉180°，把已知的AB=AC，BD=ED的等量關系分散到兩個三角形的對應邊，構造全等，再運用全等三角形解決問題.

總之，利用旋轉變換解決問題體現了思維的多向性、滲透了“分散與集中”的化歸思想，難度較大，在解決問題時，學生真正困惑的是：什么時候需要旋轉變換？什么時候需要構造旋轉圖形？怎么構造旋轉圖形？因此，在平常教學中，我們可以先讓學生理解旋轉變換中的基本圖形、熟悉旋轉變換的常見模型，引導學生從“條件分析入手確定是否需要旋轉、觀察圖形尋找旋轉目標、思考如何旋轉（旋轉中心、旋轉方向、旋轉角度）”三個程序去解決問題，從而養成看圖、畫圖、遷移等“程序化”的做題習慣，這樣便能進一步體會到旋轉變換解決問題是“有章可循”的，對這一類問題不會再束手無策，解題的速度和質量也會逐步提高.